LeetCode 1206.设计跳表：算法详解

Tisfy2025-02-27 20:47

【LetMeFly】1206.设计跳表：算法详解

力扣题目链接：https://leetcode.cn/problems/design-skiplist/

不使用任何库函数，设计一个 跳表 。

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

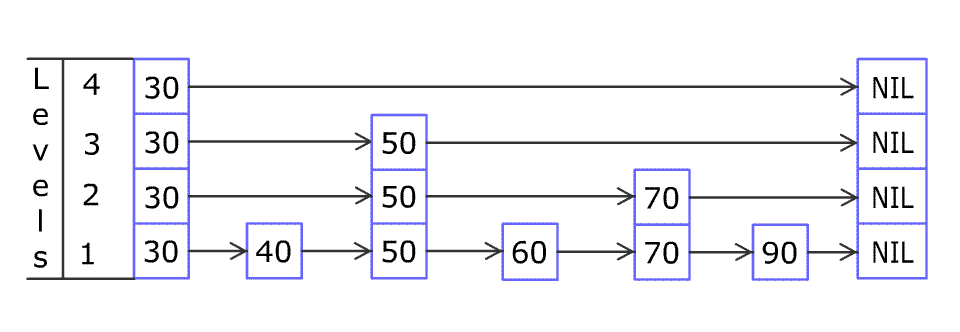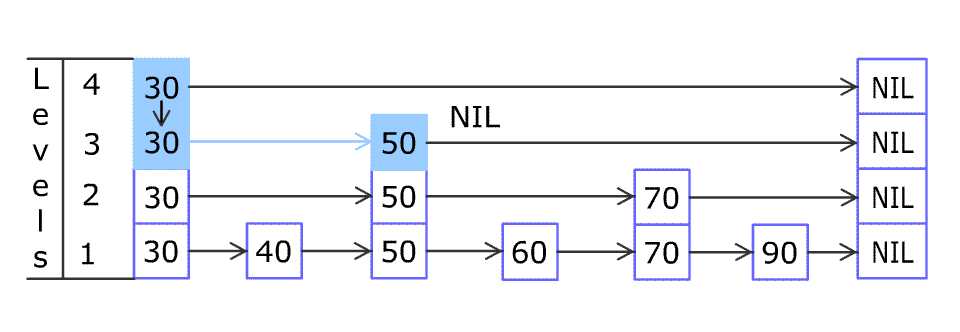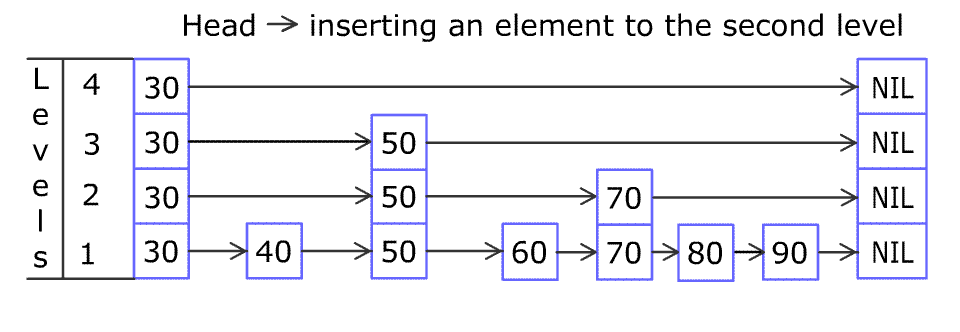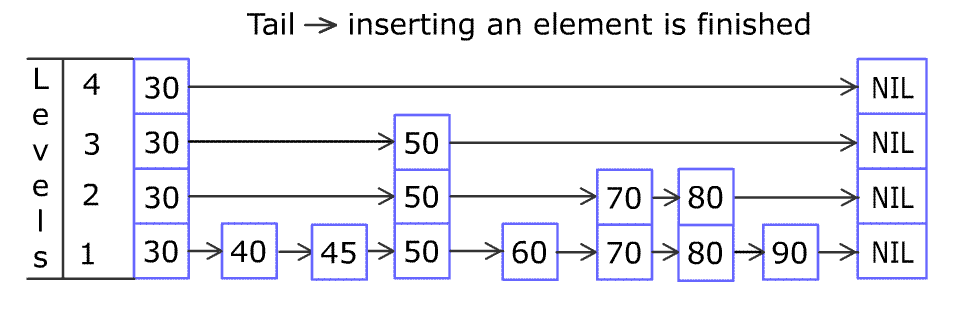
跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://oi-wiki.org/ds/skiplist/

在本题中，你的设计应该要包含这些函数：

  • bool search(int target) : 返回target是否存在于跳表中。
  • void add(int num): 插入一个元素到跳表。
  • bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

复制代码 
输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

提示:

  • 0 <= num, target <= 2 * 10^4^
  • 调用search, add, erase操作次数不大于 5 * 10^4^

设计跳表

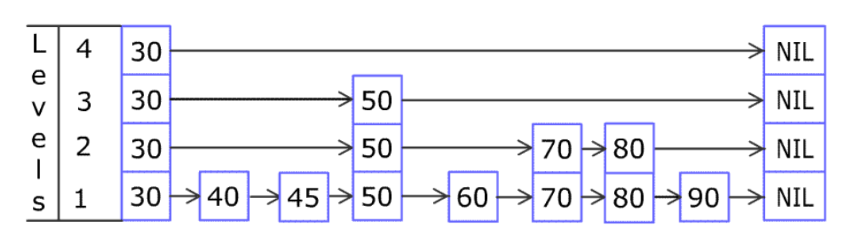
链表查询复杂度是 O ( n ) O(n) O(n)，因为要从头到尾遍历。怎么解决这个问题？多几层链表(最下层level1是全链表)，上层链表元素少，先查上层（查一次就能跳过level1好多元素），再查下层，最终查到level1。

节点设计

对于一个节点（例如 50 50 50），我们可以只创建一个 50 50 50节点，并分别保留这个节点在level1到level3的下一个节点。

cpp 复制代码 
class SkiplistNode {
public:
    int value;
    vector<SkiplistNode*> next;

    SkiplistNode(int val, int level): value(val), next(level) {}  // 一个节点一旦生成，level就是固定的
};
cpp 复制代码 
class Skiplist {
private:
    SkiplistNode* head;  // 为了方便，统一添加头节点
    int level;  // 当前跳表层数，可依据实际数据范围确定
public:
    Skiplist() {
        head = new SkiplistNode(-1, MAX_LEVEL);  // 每层一旦出现，就一定需要head节点
        level = 0;
    }
    
    bool search(int target) {}
    
    void add(int num) {}
    
    bool erase(int num) {}
};

查询

  • 每一层的查询依据是：找到最后一个严格小于 t a r g e t target target的节点；
  • 上层到下层的依据是：同一个节点直接下移一层。

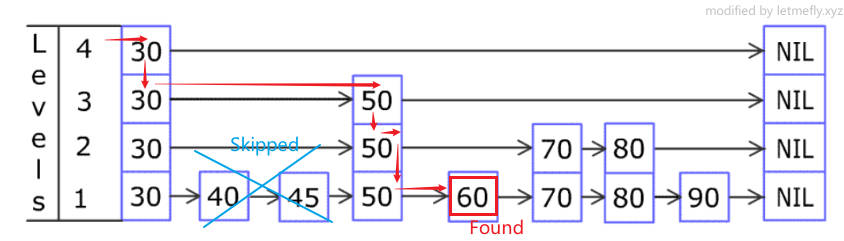
例如上图要查询元素 60 60 60：

  1. 先从最上层(level4)开始查询， 30 30 30是最后一个小于 60 60 60的元素，在 30 30 30停止，跳到level3的 30 30 30
  2. level3从 30 30 30开始向右查询， 50 50 50是最后一个小于 60 60 60的元素，直接跳到 50 50 50（可以发现最下层的 40 40 40和 45 45 45d都被跳过了），跳到level2的 50 50 50
  3. level2从 50 50 50开始向右查询，最后一个小于 60 60 60的节点就是 50 50 50，停止并跳到level1的 50 50 50
  4. level1从 50 50 50开始向右查询，最后一个小于 60 60 60的节点就是 50 50 50，停止。

最终停止的节点是level1的 50 50 50。

注意：

  1. 最终一定停止在level1
  2. 每一层都是在最后一个严格小于target的节点停止并移动到下层(如有)
  3. 所查询节点就是最终停止到的节点的右边相邻节点
cpp 复制代码 
bool search(int target) {
	SkiplistNode* p = head;  // 从头节点开始
    for (int i = level - 1; i >= 0; i--) {  // 从上层到下层
        while (p->next[i] && p->next[i]->value < target) {  // 每一层找到最后一个严格小于target的节点
            p = p->next[i];
        }
    }
    p = p->next[0];  // 最终停止到了level1的50，50在level1的next就是待查找的60
    return p && p->value == target;
}

插入

新增一个节点，这个节点都要在哪些层出现呢？直接rand呗。每个节点都要在最下层出现，可以定义一个全局概率 P P P，表示这个节点有 P P P的概率在上一层再出现一次。

对于本题，要求复杂度 log ⁡ 2 n \log_2 n log2n所以可取 P = 1 2 P=\frac12 P=21；最多50000次操作， log ⁡ 2 50000 ≈ 15.6 \log_2 50000\approx 15.6 log250000≈15.6，因此可取最大层数 15 15 15。

cpp 复制代码 
int randLevel() {
    int ans = 1;
    while (ans < MAX_LEVEL && rand() < p) {
        ans++;
    }
    return ans;
}

对于新增节点 n u m num num，假设随机出来确定它要在 l e v e l 1 level_1 level1到 l e v e l n e w L e v e l level_{newLevel} levelnewLevel层出现，那么就可以创建一个大小为 n e w L e v e l newLevel newLevel的 u p d a t e update update数组，其中 u p d a t e [ i ] = p update[i]=p update[i]=p代表 l e v e l i + 1 level_{i+1} leveli+1层 p p p元素的 n e x t next next需要修改为指向新节点。

确定 u p d a t e update update数组的方法和查询类似，每层找到最后一个严格小于 n u m num num的节点即可。

cpp 复制代码 
void add(int num) {
    int newLevel = randLevel();
    vector<SkiplistNode*> update(newLevel, head);  // 默认值为head
    SkiplistNode* p = head;
    for (int i = level - 1; i >= 0; i--) {
        while (p->next[i] && p->next[i]->value < num) {  // 每层找最后一个严格小于num的节点
            p = p->next[i];
        }
        if (i < newLevel) {  // 只有低newLevel层需要插入p节点
            update[i] = p;
        }
    }

    level = max(level, newLevel);  // 更新跳表最大层数
    SkiplistNode* newNode = new SkiplistNode(num, newLevel);
    for (int i = 0; i < newLevel; i++) {  // 低newLevel层每层插入新节点
        newNode->next[i] = update[i]->next[i];
        update[i]->next[i] = newNode;
    }
}

删除

删除和新增类似，找到每层需要更新next的节点，更新next并更新层数。

与插入不同的是，在开始遍历前不知道 n u m num num一共有几层，所以我们可以初始化 u p d a t e update update大小为当前跳表的总层数。在真正删除节点时从最下层往最上层删除，一旦update[i]的next不是目标节点了就直接break。

注意，若 n u m num num本身就不再跳表中就不要误删其他元素了。

删除完目标节点后，从上到下遍历确定是否有空层（head的next直接为null）需要删除即可。

cpp 复制代码 
bool erase(int num) {
    vector<SkiplistNode*> update(level);  // 其实并不需要初始值
    SkiplistNode* p = head;
    for (int i = level - 1; i >= 0; i--) {
        while (p->next[i] && p->next[i]->value < num) {  // 每层找最后一个严格小于num的节点
            p = p->next[i];
        }
        update[i] = p;
    }
    
    p = p->next[0];  // 目标节点
    if (!p || p->value != num) {  // num在跳表中根本不存在
        return false;
    }
    
    for (int i = 0; i < level; i++) {  // 从下往上开始删除目标节点
        if (update[i]->next[i] != p) {
            break;
        }
        update[i]->next[i] = p->next[i];
    }
    delete p;

    while (level > 0 && !head->next[level - 1]) {  // "移除"空层
        level--;
    }
    return true;
}

时空复杂度

  • 时间复杂度：单次操作 O ( log ⁡ n ) O(\log n) O(logn)
  • 空间复杂度 O ( n ) O(n) O(n)

AC代码

C++

cpp 复制代码 
const int MAX_LEVEL = 15;
const double p = 0.5;

class SkiplistNode {
public:
    int value;
    vector<SkiplistNode*> next;

    SkiplistNode(int val, int level): value(val), next(level) {}  // 一个节点一旦生成，level就是固定的
};

class Skiplist {
private:
    SkiplistNode* head;
    int level;

    int randLevel() {
        int ans = 1;
        while (ans < MAX_LEVEL && rand() < p) {
            ans++;
        }
        return ans;
    }
public:
    Skiplist() {
        head = new SkiplistNode(-1, MAX_LEVEL);  // 每层一旦出现，就一定需要head节点
        level = 0;
    }
    
    bool search(int target) {
        SkiplistNode* p = head;
        for (int i = level - 1; i >= 0; i--) {
            while (p->next[i] && p->next[i]->value < target) {
                p = p->next[i];
            }
        }
        p = p->next[0];
        return p && p->value == target;
    }
    
    void add(int num) {
        int newLevel = randLevel();
        vector<SkiplistNode*> update(newLevel, head);
        SkiplistNode* p = head;
        for (int i = level - 1; i >= 0; i--) {
            while (p->next[i] && p->next[i]->value < num) {
                p = p->next[i];
            }
            if (i < newLevel) {
                update[i] = p;
            }
        }

        level = max(level, newLevel);
        SkiplistNode* newNode = new SkiplistNode(num, newLevel);
        for (int i = 0; i < newLevel; i++) {
            newNode->next[i] = update[i]->next[i];
            update[i]->next[i] = newNode;
        }
    }
    
    bool erase(int num) {
        vector<SkiplistNode*> update(level);
        SkiplistNode* p = head;
        for (int i = level - 1; i >= 0; i--) {
            while (p->next[i] && p->next[i]->value < num) {
                p = p->next[i];
            }
            update[i] = p;
        }
        
        p = p->next[0];
        if (!p || p->value != num) {
            return false;
        }
        
        for (int i = 0; i < level; i++) {
            if (update[i]->next[i] != p) {
                break;
            }
            update[i]->next[i] = p->next[i];
        }
        delete p;

        while (level > 0 && !head->next[level - 1]) {
            level--;
        }
        return true;
    }
};

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist* obj = new Skiplist();
 * bool param_1 = obj->search(target);
 * obj->add(num);
 * bool param_3 = obj->erase(num);
 */

Python

python 复制代码 
from typing import List, Any
import random


MAX_LEVEL = 15
P = 0.5

class SkiplistNode:
    def __init__(self, v: int, level: int):
        self.value = v
        self.next: List[SkiplistNode] = [None] * level

class Skiplist:
    def __init__(self):
        self.head = SkiplistNode(-1, MAX_LEVEL)
        self.level = 0
    
    def __randLevel(self):
        ans = 1
        while ans < MAX_LEVEL and random.random() < P:
            ans += 1
        return ans

    def search(self, target: int) -> bool:
        p = self.head
        for i in range(self.level - 1, -1, -1):
            while p.next[i] and p.next[i].value < target:
                p = p.next[i]
        p = p.next[0]
        # return p and p.value == target  # 不可！p为None的化这一行会return None而不是False！
        return p is not None and p.value == target

    def add(self, num: int) -> None:
        newLevel = self.__randLevel()
        update = [self.head] * newLevel
        p = self.head
        for i in range(self.level - 1, -1, -1):
            while p.next[i] and p.next[i].value < num:
                p = p.next[i]
            if i < newLevel:
                update[i] = p
        
        self.level = max(self.level, newLevel)
        newNode = SkiplistNode(num, newLevel)
        for i in range(newLevel):
            newNode.next[i] = update[i].next[i]
            update[i].next[i] = newNode

    def erase(self, num: int) -> bool:
        update: List[SkiplistNode | Any] = [None] * self.level
        p = self.head
        for i in range(self.level - 1, -1, -1):
            while p.next[i] and p.next[i].value < num:
                p = p.next[i]
            update[i] = p
        
        p = p.next[0]
        if not p or p.value != num:
            return False
        
        for i in range(self.level):
            if update[i].next[i] != p:
                break
            update[i].next[i] = p.next[i]
        while self.level > 0 and not self.head.next[self.level - 1]:
            self.level -= 1
        return True


# Your Skiplist object will be instantiated and called as such:
# obj = Skiplist()
# param_1 = obj.search(target)
# obj.add(num)
# param_3 = obj.erase(num)

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源

相关推荐
Liu_Meihao17 分钟前
【算法】798. 差分矩阵
线性代数·算法·矩阵
楼台的春风1 小时前
【图像的读写与基本操作】
图像处理·人工智能·深度学习·opencv·算法·计算机视觉·嵌入式
FeiCat Henry1 小时前
KGG转MP3工具|非KGM文件|解密音频
科技·算法·音视频·软件工程·视频编解码
小喵要摸鱼2 小时前
【Python LeetCode】面试经典 150 题
python·leetcode·面试
因兹菜2 小时前
[LeetCode]day29 232.用栈实现队列
redis·算法·leetcode
tianmu_sama2 小时前
[Linux高性能服务器编程] 多线程编程
linux·服务器·c++·算法
JKHaaa3 小时前
单链表的排序（C++）
数据结构·c++·算法
nqqcat~3 小时前
C语言机试编程题
c语言·开发语言·考研·算法
阳光男孩014 小时前
力扣2454. 下一个更大元素 IV
算法·leetcode·职场和发展
热门推荐
01DeepSeek各版本说明与优缺点分析02本地部署DeepSeek教程（Mac版本）03如何在WPS和Word/Excel中直接使用DeepSeek功能04DeepSeek R1本地化部署 Ollama + Chatbox 打造最强 AI 工具05太炸裂了！清华大学deepseek从入门到精通使用手册又出第三版了，《普通人如何抓住DeepSeek红利》（无套路，直接下载）06DeepSeek本地部署详细指南07本地化部署AI知识库：基于Ollama+DeepSeek+AnythingLLM保姆级教程08保姆级教程：利用Ollama与Open-WebUI本地部署 DeedSeek-R1大模型09DeepSeek r1本地安装全指南10从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑