- 十大排序算法
-
- [比较类排序(Comparison Sort)](#比较类排序(Comparison Sort))
-
- [快速排序(Quick Sort)](#快速排序(Quick Sort))
- [归并排序(Merge Sort)](#归并排序(Merge Sort))
- [堆排序(Heap Sort)](#堆排序(Heap Sort))
- [希尔排序(Shell Sort)](#希尔排序(Shell Sort))
- [插入排序(Insertion Sort)](#插入排序(Insertion Sort))
- [冒泡排序(Bubble Sort)](#冒泡排序(Bubble Sort))
- [选择排序(Selection Sort)](#选择排序(Selection Sort))
- [2. 非比较类排序(Non-Comparison Sort)](#2. 非比较类排序(Non-Comparison Sort))
十大排序算法
虽然 sorted() 函数可以完成排序任务,但学习 十大经典排序算法 仍然很有价值。
- 深入理解排序原理
sorted()只是 Python 提供的工具,本质上它使用的是Timsort(归并 + 插入排序) 。学习排序算法可以帮助理解 不同算法的时间复杂度、空间复杂度和适用场景 ,能根据需求选择合适的排序方法。如果不了解排序算法的原理,在面对不同场景时,可能会做出低效或错误的选择。例如:
- 为什么 Python 选择 Timsort?
- 为什么快速排序在大多数情况下比归并排序更快?
- 为什么插入排序在数据基本有序时反而更高效?
- 处理特殊需求
有些情况下,内置sorted()并不能满足所有需求,而自定义排序算法可以提供更好的优化。例如:
- 大数据排序(外部排序):在数据量超大,无法全部放入内存时,可能需要归并排序或堆排序。
- 稳定排序 vs. 不稳定排序 :
sorted()是稳定排序,但如果不需要稳定性,可以用更快的不稳定排序(如快速排序)。- 多关键字排序:需要按照多个字段进行排序时,可能需要定制化的比较规则。
参考:十大经典排序算法 动图、Sorting Algorithms
简单理解:
-
比较排序:靠元素间 "比大小" 排序
-
非比较排序:靠 "特征" 直接定位
-
稳定排序(Stable Sorting):排序后 相等的元素 仍然 保持它们原本的相对顺序,则称该排序算法是稳定的。
-
不稳定排序(Unstable Sorting):排序后 相等的元素相对位置可能发生变化,则该算法是不稳定的。
-
内部排序(Internal Sorting) :如果 排序完全在内存中完成,不涉及外部存储(如磁盘、数据库等),则称为内部排序。
-
外部排序(External Sorting) :如果数据量太大,无法一次性放入内存,需要 借助磁盘、数据库等存储来进行排序,则称为外部排序。
比较类排序(Comparison Sort)
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 快速排序 | O(n log n) | O(n log n) | O(n²) | O(log n) | 内部排序 | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 外部排序 | 稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 内部排序 | 不稳定 |
| 希尔排序 | O(n log n) | O(n log² n) | O(n²) | O(1) | 内部排序 | 不稳定 |
| 插入排序 | O(n²) | O(n) | O(n²) | O(1) | 内部排序 | 稳定 |
| 冒泡排序 | O(n²) | O(n) | O(n²) | O(1) | 内部排序 | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 内部排序 | 不稳定 |
特点:
- 必须通过元素之间的比较进行排序(不能"直接确定"元素的位置)。
- 无法突破 O(n log n) 的时间复杂度下界 (基于 决策树模型 的理论下界)。
- 适用于所有数据类型(不论是整数、字符串还是对象,只要支持比较操作)。
快速排序(Quick Sort)
快速排序通常是处理 大规模数据排序 时的 首选算法之一,尤其是在数组数据结构中。通过合理选择基准元素和优化递归过程,快速排序可以非常高效。
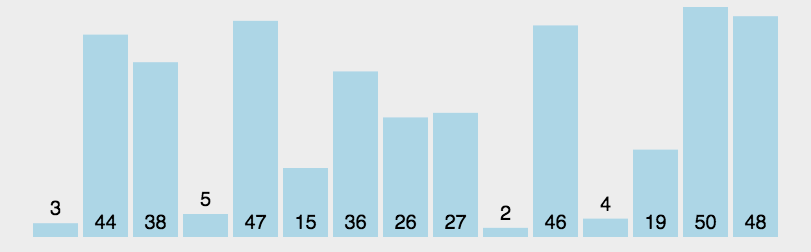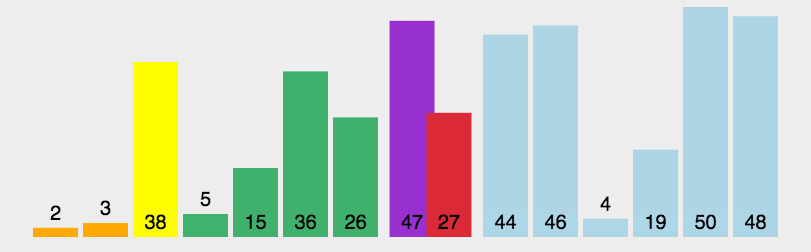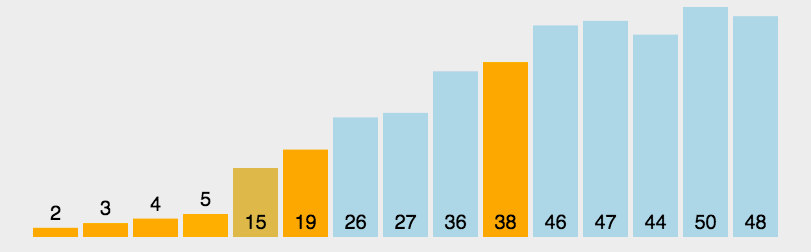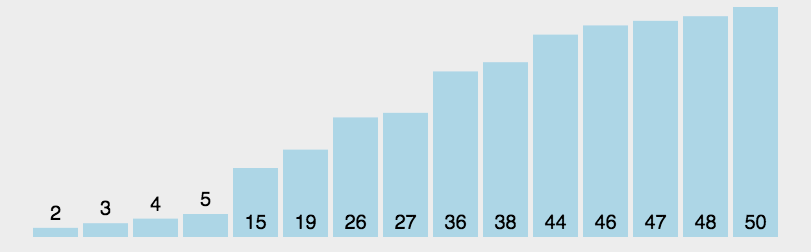
快速排序是一种基于 分治法(Divide and Conquer) 的排序算法,
- 从数列中挑出一个元素,称为 "基准"(
pivot); - 重新排序数列,比基准值小的放在基准前面,比基准值大的放在基准后面 (相同的数可以到任一边)。在这个分区退出之后,该 基准就处于数列的中间位置 。这个称为 分区(
partition)操作; - 递归地(
recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
python
def quick_sort(arr):
# 基本情况:数组长度为0或1时,已经有序
if len(arr) <= 1:
return arr
# 选择基准元素,通常选择第一个元素作为基准
pivot = arr[0]
# 分割数组:小于等于基准元素的部分,和大于基准元素的部分
left = [x for x in arr[1:] if x <= pivot]
right = [x for x in arr[1:] if x > pivot]
# 递归排序并合并结果
return quick_sort(left) + [pivot] + quick_sort(right)
nums = [5, 3, 8, 4, 2]
sorted_nums = quick_sort(nums)
print("排序后:", sorted_nums) # [2, 3, 4, 5, 8]归并排序(Merge Sort)
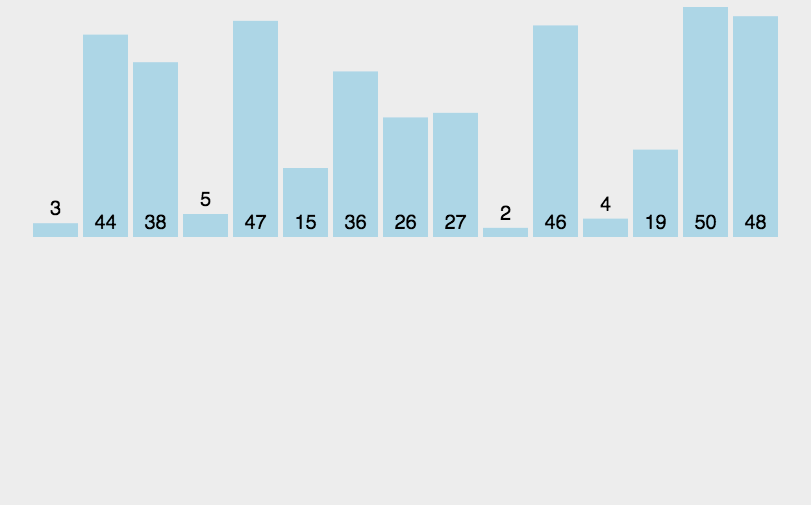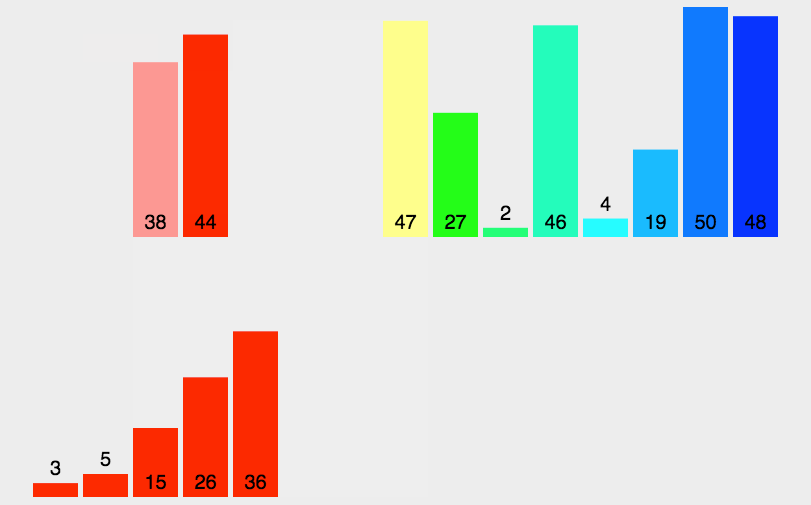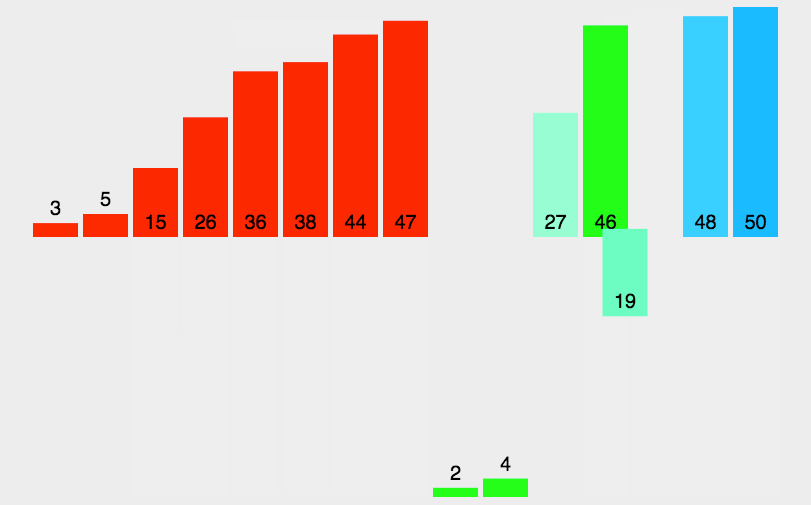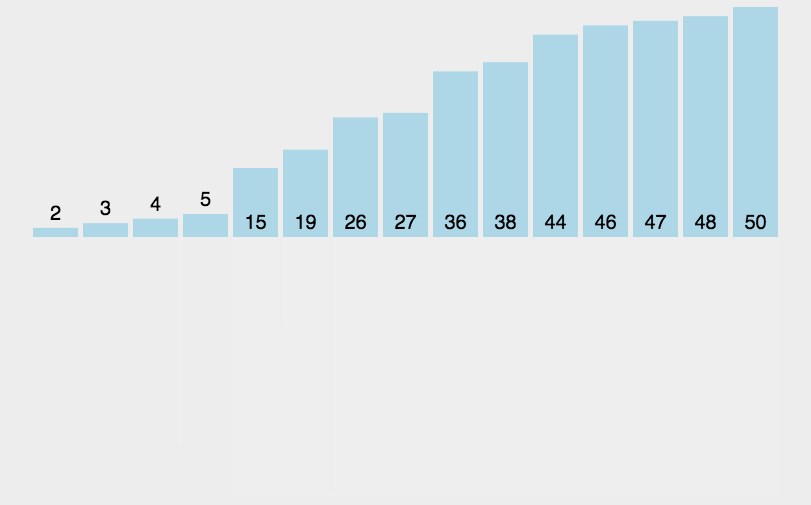
归并排序是一种 **分治法(Divide and Conquer)**的排序算法。
核心思想是:将大问题 分解 成小问题,递归 地解决小问题,再将小问题的解决方案 合并 起来。
python
def merge_sort(arr):
if len(arr) <= 1:
return arr # 基本情况:数组长度小于等于1时已经有序
# 将数组从中间分割成两半
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
# 递归排序两半
left_sorted = merge_sort(left_half)
right_sorted = merge_sort(right_half)
# 合并两半有序数组
return merge(left_sorted, right_sorted)
def merge(left, right):
result = []
i = j = 0
# 比较左右两个数组的元素,按顺序放入 result 中
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# 将剩余的元素加入 result 中
result.extend(left[i:])
result.extend(right[j:])
return result
nums = [5, 3, 8, 4, 2]
sorted_nums = merge_sort(nums)
print("排序后:", sorted_nums) # [2, 3, 4, 5, 8]堆排序(Heap Sort)
堆排序是一种基于 堆数据结构 的排序算法。堆是一种 完全二叉树,其中满足特定的顺序性质:
- 大根堆(Max Heap):每个父节点的值都大于或等于其子节点的值。
- 小根堆(Min Heap):每个父节点的值都小于或等于其子节点的值。
堆排序的核心思想是:
- 构建堆:将待排序的数组转换成一个堆结构。
- 堆化:将堆顶元素(最大值或最小值)和堆底元素交换,然后对剩下的堆进行调整(维护堆的性质)。
- 递归调整堆:重复上一步骤,直到堆的大小为 1,即数组已经排好序。
希尔排序(Shell Sort)
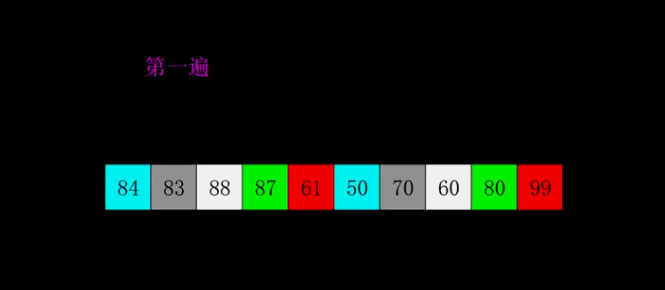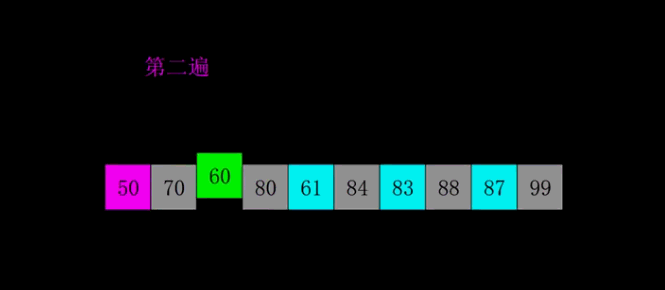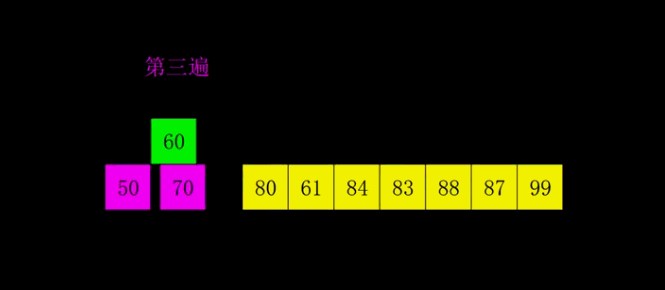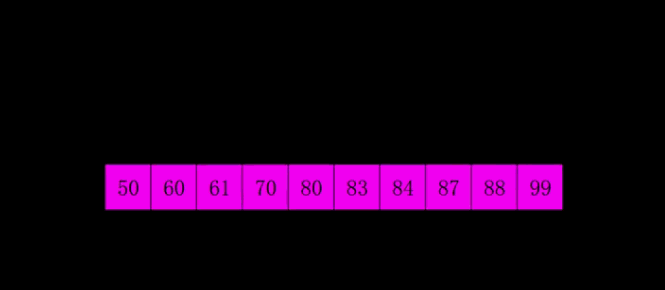
希尔排序是 插入排序的一种改进版本 ,它通过将数据 分为多个子序列 来减少元素的移动次数。具体来说,希尔排序会使用一个称为 "增量" 的参数,首先 将数据按增量分组 进行插入排序,然后 逐渐减小增量,直到增量为 1,此时的插入排序会更加高效。
希尔排序的核心思想是:通过 分组 来减少元素的移动,改进插入排序的效率。
python
def shell_sort(array):
n = len(array)
gap = n // 2 # 增量
while gap > 0:
for i in range(gap, n):
for j in range(i, gap-1, -gap):
if array[j] < array[j-gap]:
array[j], array[j-gap] = array[j-gap], array[j]
else:
break
gap //= 2 # 减小增量
return array
nums = [5, 3, 8, 4, 2]
sorted_nums = shell_sort(nums)
print("排序后:", sorted_nums) # [2, 3, 4, 5, 8]插入排序(Insertion Sort)
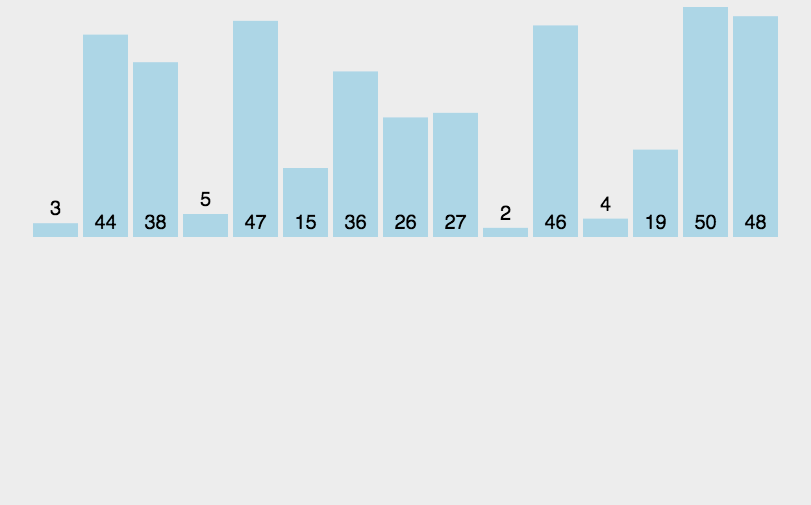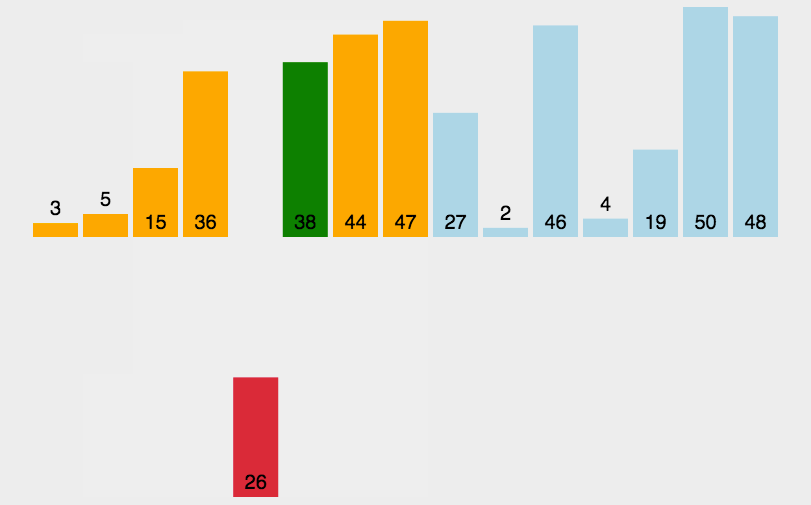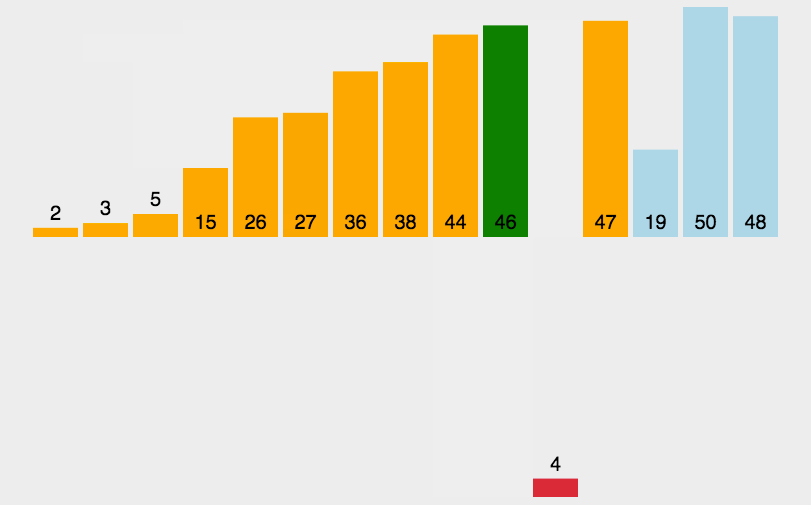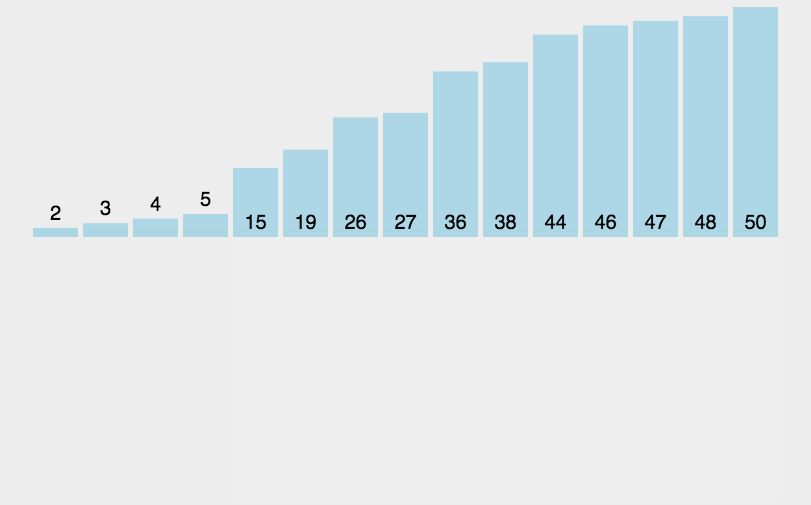
插入排序的思想,就像 打扑克牌理牌 的过程。你手上的牌 从左往右插入,让它们逐步保持有序。
每次从 未排序的元素中取出一个 ,插入到前面已排好序的位置中。
python
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i] # 当前待插入的元素
j = i - 1
# 向前查找合适的位置
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j] # 元素右移
j -= 1
arr[j + 1] = key # 插入到正确位置
return arr
nums = [5, 3, 8, 4, 2]
sorted_nums = insertion_sort(nums)
print("排序后:", sorted_nums) # [2, 3, 4, 5, 8]冒泡排序(Bubble Sort)
正如图中所示,重复地 比较相邻的两个元素 (绿色),如果它们的顺序错误就把它们交换 过来。大的元素会像"泡泡"一样一步步"冒"到最后(黄色)。
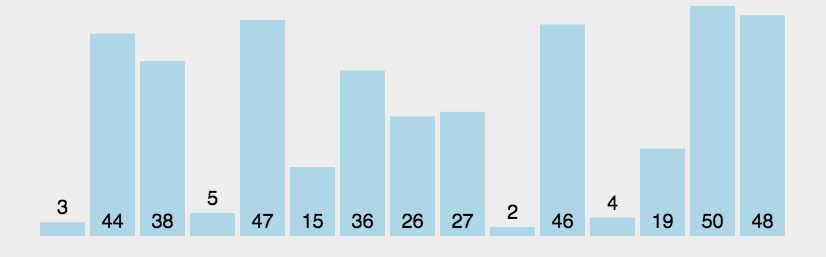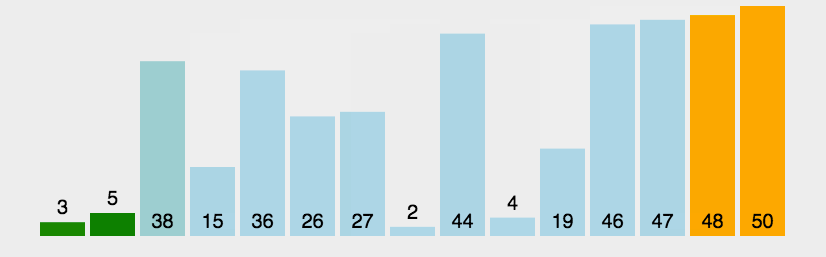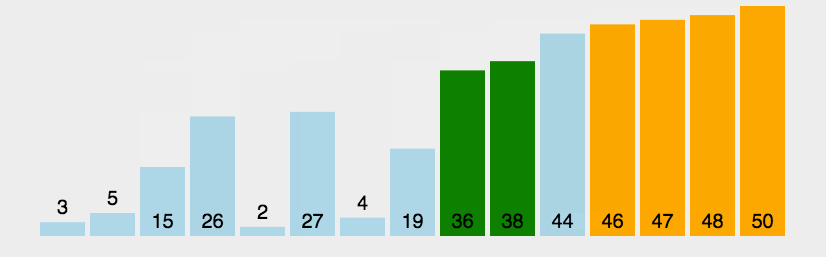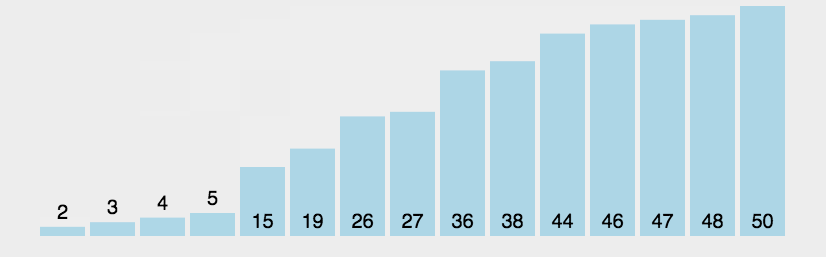
python
def bubble_sort(arr):
n = len(arr)
for i in range(n): # 总共需要进行 n 次遍历
for j in range(0, n - 1 - i): # 每次减少已排好的元素
if arr[j] > arr[j + 1]: # 相邻元素比较
arr[j], arr[j + 1] = arr[j + 1], arr[j] # 交换位置
return arr
nums = [5, 3, 8, 4, 2]
sorted_nums = bubble_sort(nums)
print("排序后:", sorted_nums) # [2, 3, 4, 5, 8]【优化】可以加一个标志变量 swapped,如果 某一轮没有发生交换,说明已经有序了,提前结束排序:
python
def bubble_sort_optimized(arr):
n = len(arr)
for i in range(n):
swapped = False
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
if not swapped: # 没有交换,提前 return
break
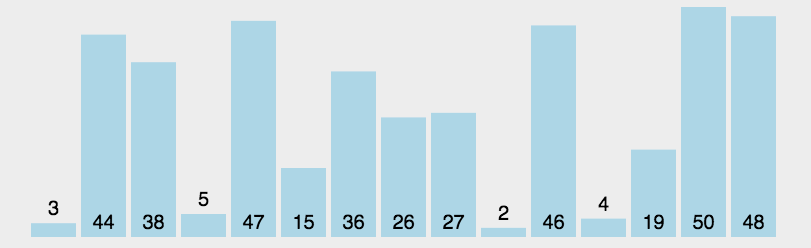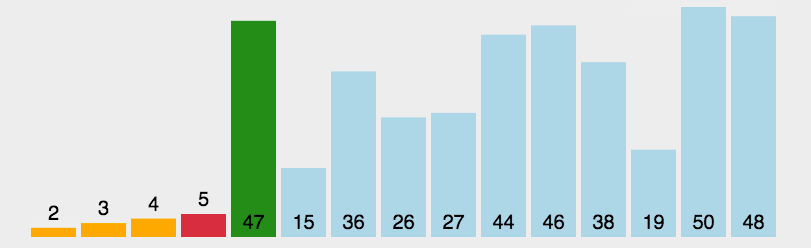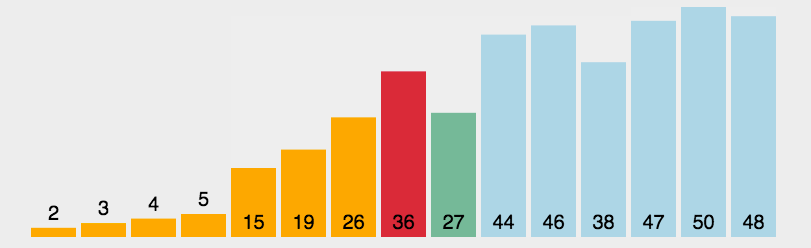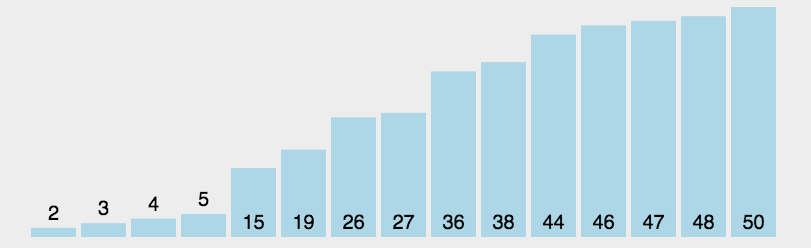
return arr选择排序(Selection Sort)
简单直观:每一轮从 未排序 的元素中 "选择"一个最小的(或最大的) ,然后 放到已排序序列的末尾。
python
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_index = i # 假设当前位置 i 是最小值
for j in range(i + 1, n):
if arr[j] < arr[min_index]:
min_index = j # 找到更小的元素索引
arr[i], arr[min_index] = arr[min_index], arr[i] # 交换位置
return arr
nums = [5, 3, 8, 4, 2]
sorted_nums = selection_sort(nums)
print("排序后:", sorted_nums) # [2, 3, 4, 5, 8]2. 非比较类排序(Non-Comparison Sort)
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(k) | 外部排序 | 稳定 |
| 桶排序 | O(n + k) | O(n + k) | O(n²) | O(n + k) | 外部排序 | 稳定 |
| 基数排序 | O(n × k) | O(n × k) | O(n × k) | O(n + k) | 外部排序 | 稳定 |
特点:
- 不依赖元素的比较,而是利用元素的某些特征(如数值范围、位数等)进行排序。
- 有可能突破 O(n log n) 的时间复杂度,但通常会占用额外的存储空间。
- 数据有特定要求 ,通常仅适用于整数、字符串等可进行"直接定位"的数据。