引言
今天的每日一题原题是2278. 字母在字符串中的百分比,直接模拟,逐个匹配,统计letter在原始字符串s中出现的次数,然后再计算所占百分比即可。更换成前几天遇到的更有意思的一题来写这个每日一题。
题目
给你一个下标从 0 开始的整数数组 nums 。对于每个下标 i(1 <= i <= nums.length - 2),nums[i] 的 美丽值 等于:
2,对于所有0 <= j < i且i < k <= nums.length - 1,满足nums[j] < nums[i] < nums[k]1,如果满足nums[i - 1] < nums[i] < nums[i + 1],且不满足前面的条件0,如果上述条件全部不满足
返回符合 1 <= i <= nums.length - 2 的所有 nums[i] 的 美丽值的总和 。
示例 1:
输入:nums = [1,2,3]
输出:2
解释:对于每个符合范围 1 <= i <= 1 的下标 i :
- nums[1] 的美丽值等于 2示例 2:
输入:nums = [2,4,6,4]
输出:1
解释:对于每个符合范围 1 <= i <= 2 的下标 i :
- nums[1] 的美丽值等于 1
- nums[2] 的美丽值等于 0示例 3:
输入:nums = [3,2,1]
输出:0
解释:对于每个符合范围 1 <= i <= 1 的下标 i :
- nums[1] 的美丽值等于 0提示:
3 <= nums.length <= 1051 <= nums[i] <= 105
思路
首先还是读懂题目,对于符合1 <= i <= nums.length - 2的下标i,美丽值可能有3种情况:
- 美丽值 = 2,对于在i位置前面的数,都严格小于
nums[i];且在i位置后面的数,都严格大于nums[i] - 美丽值 = 1,无法满足第1种情况下,且可以满足
nums[i]前面的1个数严格小于它,后面的1个数严格大于它 - 美丽值 = 0,排除上述2种情况的其他情况
那么对于每个在范围内的i,我们要逐个判断美丽值:对于情况1,如果每个都去比较,判断单个i需要的时间复杂度是O(n),整体的时间复杂度就是O(n^2);对于情况2,只要判断前后,判断单个i的时间复杂度是O(1);对于情况3,在上述2种情况都判断后,不再需要单独判断。
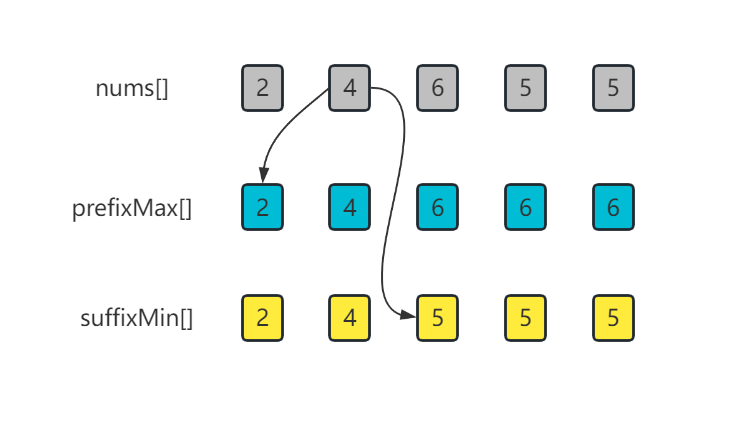
由此可见,我们主要优化点在于如何快速判断情况1。构造2个辅助数组,prefixMax[]和suffixMin[],prefixMax[i]表示下标[0, i]范围内的最大值,suffixMin[i]表示下标[i, n-1]范围内的最小值。有了这2个辅助数组后,对于位置i我们在判断是否满足情况1的时间,只要判断条件 prefixMax[i-1] < nums[i] && nums[i] < suffixMin[i+1] 即可,这样每次判断的时间复杂度会缩减到O(1),判断范围内的i的时间复杂度是O(n)。而构建这2个辅助数组,需要分别从前往后和从后往前遍历原始数组,时间复杂度也是O(n)。这样,我们就避免了O(n^2)的时间复杂度。
进一步来看,如果我们从前往后处理i的话,prefixMax[]数组不需要被创建,只要滚动维护一个prefixMax的变量,表示[0, i]范围内的最大值即可,这样,可以省下一个大小为n的数组的空间开销。同理,如果从后往前处理i的话,可以省下suffixMin[]的空间。不过,这2者不可兼得。
图解
代码
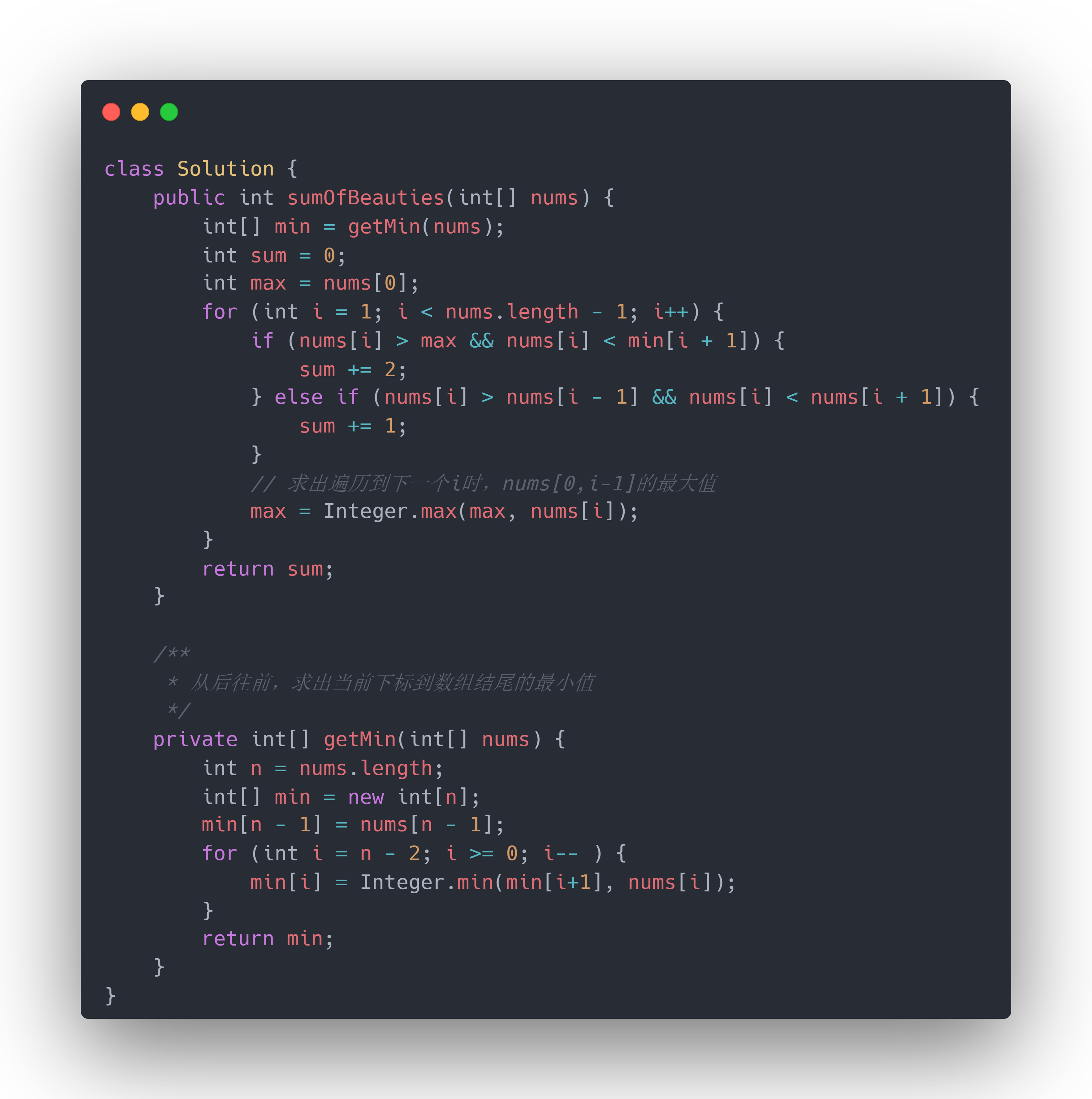
java
class Solution {
public int sumOfBeauties(int[] nums) {
int[] min = getMin(nums);
int sum = 0;
int max = nums[0];
for (int i = 1; i < nums.length - 1; i++) {
if (nums[i] > max && nums[i] < min[i + 1]) {
sum += 2;
} else if (nums[i] > nums[i - 1] && nums[i] < nums[i + 1]) {
sum += 1;
}
// 求出遍历到下一个i时,nums[0,i-1]的最大值
max = Integer.max(max, nums[i]);
}
return sum;
}
/**
* 从后往前,求出当前下标到数组结尾的最小值
*/
private int[] getMin(int[] nums) {
int n = nums.length;
int[] min = new int[n];
min[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; i-- ) {
min[i] = Integer.min(min[i+1], nums[i]);
}
return min;
}
}耗时