『Plotly实战指南』--散点图绘制进阶篇

在数据分析的世界里，散点图 是一种极为重要的可视化工具。

它能够直观地展示两个或多个变量之间的关系，帮助我们快速发现数据中的模式、趋势和异常点。

无论是探索变量之间的相关性，还是寻找数据中的潜在规律，散点图都扮演着不可或缺的角色。

与传统的静态图表不同，Plotly 绘制的散点图可以通过鼠标悬停、缩放和拖动等交互操作，让用户更深入地探索数据细节。

本文旨在探讨使用 Plotly 绘制散点图的高级技巧，包括多变量散点图的绘制、趋势分析方法的应用，以及如何通过这些技巧提升数据分析与可视化的能力。

1. 多变量散点图

1.1. 气泡图

气泡图是一种扩展的散点图，通过引入第三个维度（通常是气泡的大小或颜色）来表示额外的信息，适用于展示三个或更多变量之间的关系。

绘制气泡图 时，除了基本的 x、y 轴数据外，还需要定义气泡的大小（通常通过 size 参数）和颜色（通过 color 参数）。

这样，气泡图可以在二维图表中同时表达4个属性。

import plotly.express as px
import pandas as pd

# 示例数据
data = pd.DataFrame(
    {
        "x": [1, 2, 3, 4, 5],
        "y": [10, 11, 12, 13, 14],
        "size": [10, 20, 30, 40, 50],
        "color": ["A", "B", "A", "B", "A"],
    }
)

fig = px.scatter(
    data,
    x="x",
    y="y",
    size="size",
    color="color",
    hover_name="color",
    log_x=True,
    size_max=60,
)
fig.show()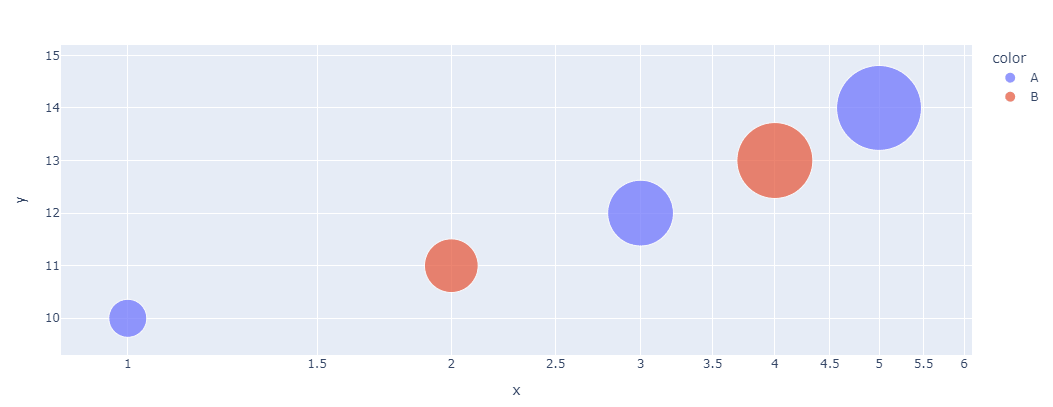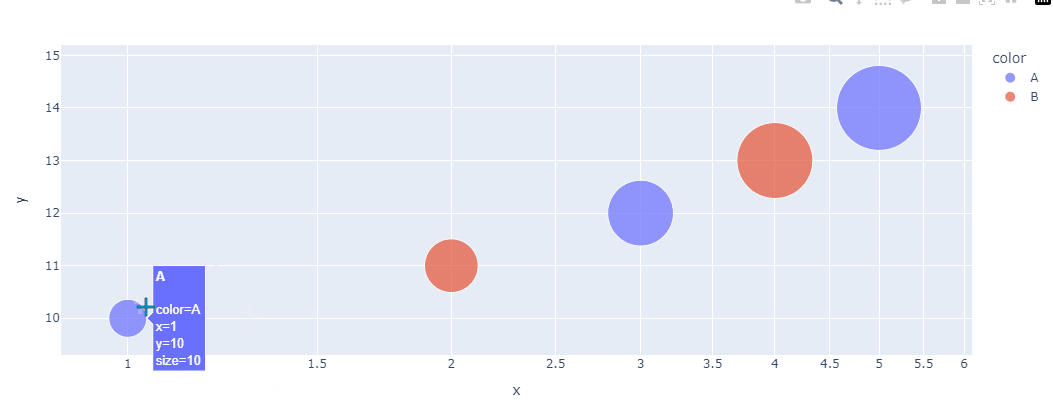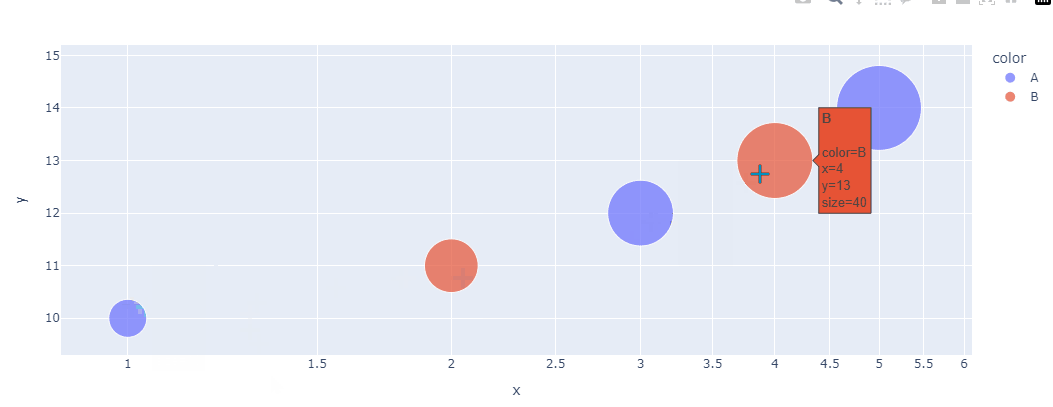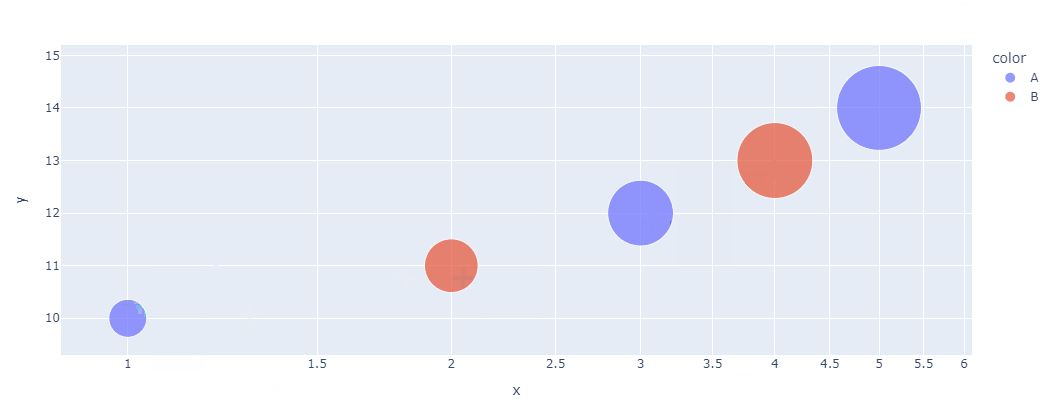

还可以通过调整颜色映射、气泡大小范围、添加标签等方式来美化气泡图，使其更加直观易懂。

1.2. 散点矩阵图

散点矩阵图是一种同时展示多个变量之间两两关系的图表，它将多个散点图排列成矩阵形式，每个单元格展示一对变量之间的散点图。

这种图表非常适合探索多变量数据之间的相关性，帮助我们快速发现变量之间的线性或非线性关系。

下面的示例中我们使用Plotly中自带的鸢尾花数据集，通过散点矩阵图可同时观察：

• 花瓣长度与宽度的相关性
• 不同花种在各维度的分布差异

import plotly.express as px
import plotly.figure_factory as ff

df = px.data.iris()
fig = ff.create_scatterplotmatrix(
    df,
    diag="histogram",
    colormap="Viridis",  # 对角线显示直方图
    width=800,
    height=800,
)
fig.update_layout(title="鸢尾花特征矩阵图")
fig.show()

通过这个图，我们可以分析鸢尾花不同属性之间的关联关系。

散点矩阵图的优点在于能够同时展示多个变量之间的关系，信息量大，并且有助于快速发现变量之间的相关性。

不过，当变量数量较多时，图表可能会显得过于复杂，难以解读，这点需要注意。

而且它对于非线性关系的展示效果也有限。

2. 散点图趋势分析法

2.1. 回归分析

回归线 是散点图中用于展示变量之间趋势关系的重要工具，

回归线通常是指线性回归模型的拟合线，用于量化变量之间的线性关系。

下面通过生成一些测试数据，通过线性模型训练之后，根据训练结果绘制散点数据的回归线。

import pandas as pd
import numpy as np
import plotly.graph_objects as go
from sklearn.linear_model import LinearRegression

# 生成示例数据
data = pd.DataFrame({
    'x': np.linspace(0, 10, 100),
    'y': 2 * np.linspace(0, 10, 100) + 3 + np.random.normal(0, 1, 100)
})

# 线性回归
# 拟合线性模型
model = LinearRegression()
model.fit(data[['x']], data['y'])
data['y_pred_linear'] = model.predict(data[['x']])

# 创建散点图
fig = go.Figure()
fig.add_trace(go.Scatter(x=data['x'], y=data['y'], mode='markers', name='原始数据'))
fig.add_trace(go.Scatter(x=data['x'], y=data['y_pred_linear'], mode='lines', name='线性回归线'))

# 显示图形
fig.show()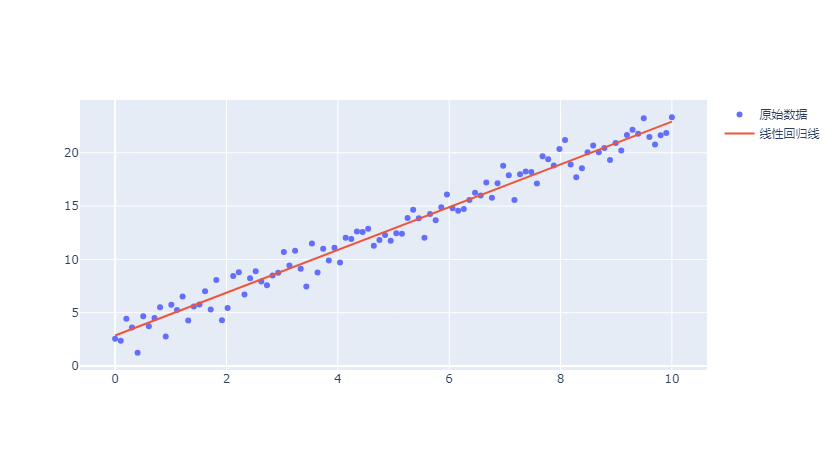

回归线可以很好的表达数据的变化趋势。

对于非线性的模型，也可以绘制对应的回归线，比如下面示例中采用的多项式回归模型训练，训练结果也可以绘制回归线。

import plotly.graph_objects as go
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# 多项式回归
# 多项式特征转换
poly = PolynomialFeatures(degree=3)
X_poly = poly.fit_transform(data[['x']])
model_poly = LinearRegression()
model_poly.fit(X_poly, data['y'])
data['y_pred_poly'] = model_poly.predict(X_poly)

fig = go.Figure()
fig.add_trace(go.Scatter(x=data['x'], y=data['y'], mode='markers', name='原始数据'))
fig.add_trace(go.Scatter(x=data['x'], y=data['y_pred_linear'], mode='lines', name='线性回归线'))
fig.add_trace(go.Scatter(x=data['x'], y=data['y_pred_poly'], mode='lines', name='多项式回归线'))

# 显示图形
fig.show()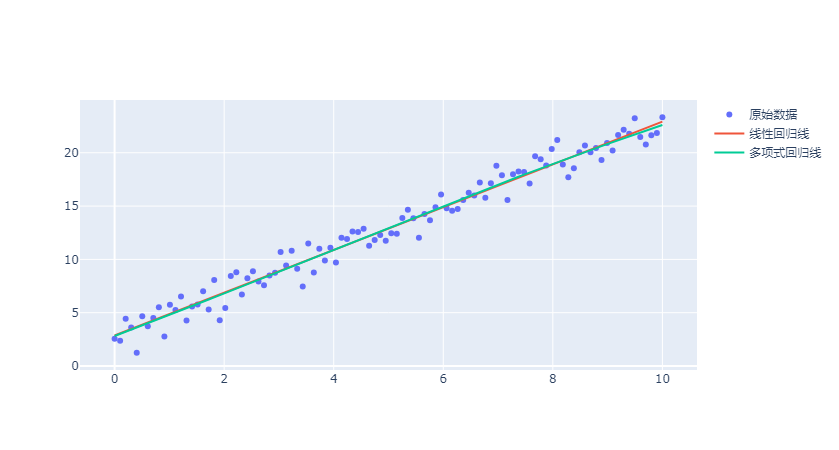

两条回归线差不多重合了。（红色是线性回归 ，青色的是多项式回归）

2.2. 平滑处理

平滑算法用于处理散点图中的噪声数据，使数据的趋势更加清晰，通过平滑处理，可以更好地观察数据的长期趋势，而忽略短期的波动。

常见平滑算法有移动平均 （通过计算一定窗口内的平均值来平滑数据）和Savitzky-Golay 滤波（一种基于多项式拟合的平滑算法）

在Plotly中，可以通过自定义函数或利用现有库（如 SciPy）来实现平滑处理并绘制曲线。

import plotly.express as px
import numpy as np
from scipy.signal import savgol_filter

# 示例数据
data = px.data.gapminder().query("country=='Canada'")
y = data["gdpPercap"]
x = np.arange(len(y))
y_smooth = savgol_filter(y, window_length=7, polyorder=2)

fig = px.scatter(data, x=x, y=y)
fig.add_scatter(x=x, y=y_smooth, mode="lines", name="平滑曲线")
fig.show()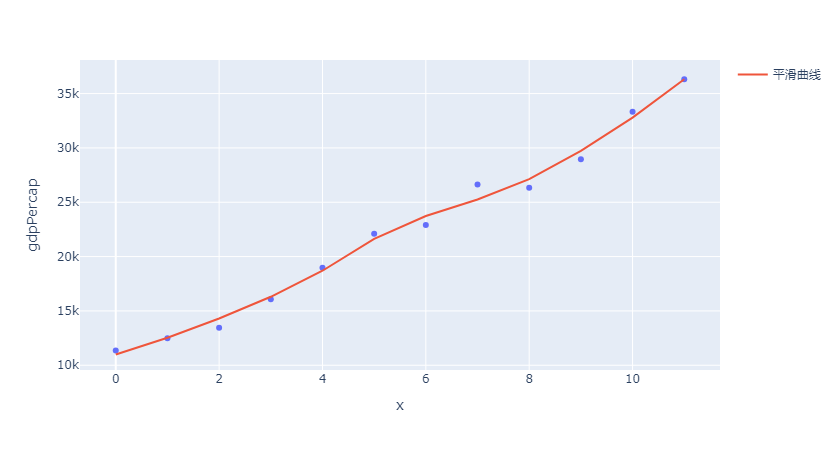

3. 总结

本文主要介绍如何使用 Plotly 绘制散点图的高级技巧，包括多变量散点图的绘制（如气泡图、散点矩阵图）和趋势分析方法（如拟合曲线、回归线、平滑算法）。

这些技巧不仅提升了数据分析的维度和深度，还通过交互式可视化增强了数据探索的效率和乐趣。