目录
[4.凸组合(Convex Combination)](#4.凸组合(Convex Combination))
[6.In-Triangle test](#6.In-Triangle test)
[8.极边(Extream Edges)](#8.极边(Extream Edges))
1.凸包

凸包就是上面蓝色皮筋围出来的范围
这些钉子可以转换到坐标轴中,横纵坐标表示颜色的比例
2.调色问题

上述问题可以进行一个抽象,抽象为一个color space

结论
- 如果有1种颜料可以被2种颜料勾兑出来,它必然位于二者之间的那条连线上
- 如果有1种颜料可以被3种颜料勾兑出来,它必然位于三角形内
- 勾兑比例与距离成反比
3.极性(Extrem)

蓝色的为极点
极点上存在一条直线,使得所有的点落在它的一侧
4.凸组合(Convex Combination)

为什么最小值必须>=0 ?
因为这种颜色大不了不用,但也不可能是负的
5.问题转化(Strategy)

如果是极点那么久不可能在一个三角形的内部,所以采用排除法,剩下的就是极点
6.In-Triangle test

遍历所有可能的三角线组合,排除非极点
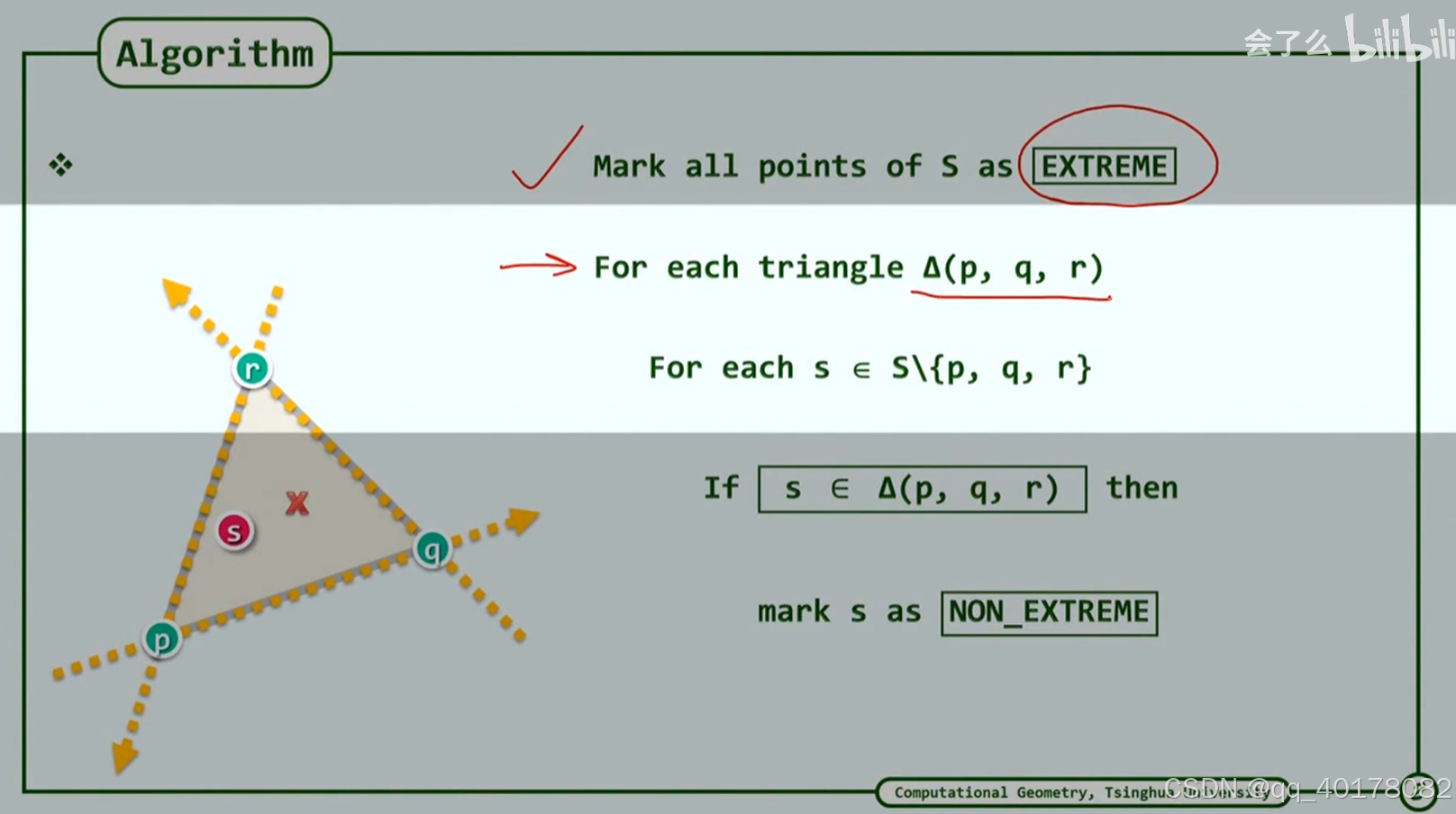
低效做法

7.To-Left-test
更加聪明的做法,如果一个点位于三条直线的left,那么它一定位于三角形内

实现(海伦公式)

只有s位于pq这条线段左侧才会取正。
8.极边(Extream Edges)
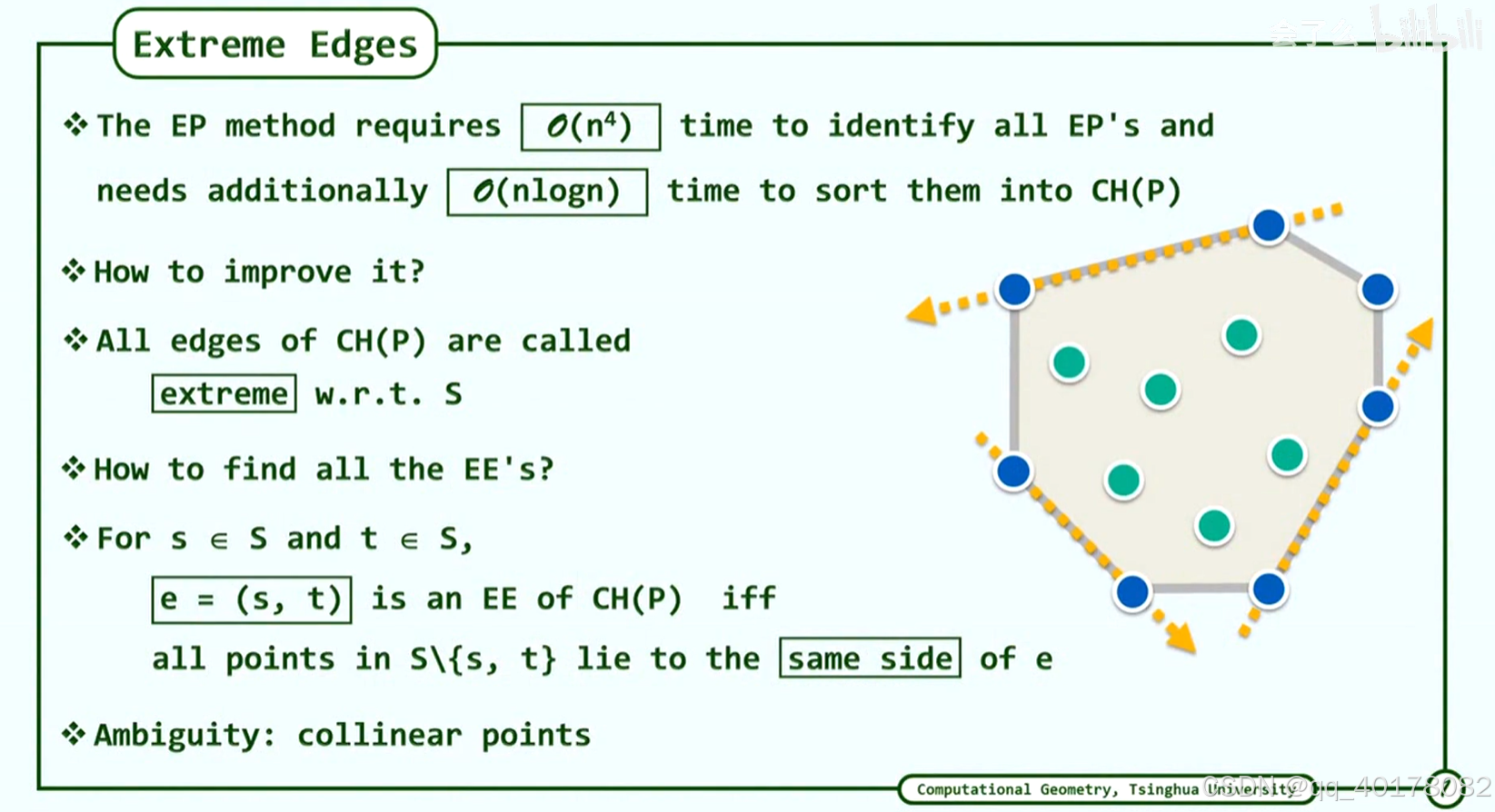
极边:所有的点落在同一侧,就是极边
算法实现



极边的算法效率高于极点的算法效率