其实是强化学习入门第一部分~
从问题定义到 Q-Learning 算法的提出。
1 任务背景
强化学习是一种学习如何从状态映射到动作 以最大化最终奖励的学习机制。智能体需要不断地在环境中进行实验,通过环境给予的反馈(奖励)来不断优化状态-行为的对应关系。
其中提及了四个要素,我们分别加以解释:
- 状态(State) :环境当前的情况,是智能体做决策的依据。
- 动作(Action) :智能体在某个状态下可以执行的操作。
- 奖励(Reward) :环境对智能体动作的即时反馈,决定行为的好坏。
- 策略(Policy) :智能体在特定状态下选择动作的规则,决定如何行动。
以 Breakout(打砖块) 为例,强化学习的任务可以概括为:让智能体通过不断试错,学习控制挡板击球,最大化清除砖块的得分,最终掌握高效连击和精准反弹的策略。
在打砖块游戏中,强化学习的四要素具体表现为:
| 要素 | Breakout示例 |
|---|---|
| 状态(State) | 历史游戏截图和操作序列 |
| 动作(Action) | 离散动作:左移、右移、不动 |
| 奖励(Reward) | 击碎砖块:+1,漏球:0,回合结束 |
| 策略(Policy) | 从当前状态到动作的映射函数 |
由此可以发现,与有监督学习和无监督学习相比,强化学习的任务具有以下特点:
- 从无标注的原始数据(视频、音频等)中学习。
- 奖励稀疏、嘈杂、延时。
- 数据间并不相互独立,而是具有时序性。
- 智能体的行为会影响后续的数据。
2 形式化问题定义
想要用算法解决问题,我们需要从具体问题中抽象出数学描述。
在强化学习框架中,智能体与环境的交互被建模为离散时间的马尔可夫决策过程(MDP),由元组 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( S , A , R , P , γ ) (\mathcal{S}, \mathcal{A}, \mathcal{R}, \mathcal{P}, \gamma) </math>(S,A,R,P,γ) 构成。
2.1 变量定义
| 变量符号 | 定义 | 说明 |
|---|---|---|
| <math xmlns="http://www.w3.org/1998/Math/MathML"> x t ∈ R x_t \in \mathcal{R} </math>xt∈R | 当前时刻 <math xmlns="http://www.w3.org/1998/Math/MathML"> t t </math>t的原始像素观测(RGB图像) | 单帧游戏画面,未经过预处理 |
| <math xmlns="http://www.w3.org/1998/Math/MathML"> a t ∈ A a_t \in \mathcal{A} </math>at∈A | 离散动作空间(如{NOOP, FIRE, RIGHT, LEFT...}) | 对应游戏手柄的18种可能操作 |
| <math xmlns="http://www.w3.org/1998/Math/MathML"> s t ∈ S s_t\in \mathcal{S} </math>st∈S | 状态空间,历史帧画面和动作的序列: <math xmlns="http://www.w3.org/1998/Math/MathML"> s t = ( x 1 , a 1 , x 2 , ... , x t ) s_t=(x_1,a_1,x_2,\dots,x_t) </math>st=(x1,a1,x2,...,xt) | 过去游戏画面和执行操作依时序拼接形成的序列 |
| <math xmlns="http://www.w3.org/1998/Math/MathML"> r t ∈ R r_t \in \mathcal{R} </math>rt∈R | 游戏引擎返回的即时奖励 | 得分变化量(可能被裁剪到[-1,1]范围) |
| <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( s ′ , r ∣ s , a ) \mathcal{P}(s′,r∣s,a) </math>P(s′,r∣s,a) | 在状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s s </math>s 执行动作 <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a 后转移到状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s ′ s′ </math>s′ 的概率并获得收益 <math xmlns="http://www.w3.org/1998/Math/MathML"> r r </math>r 的概率 | 状态转移概率函数,描述游戏环境 |
| <math xmlns="http://www.w3.org/1998/Math/MathML"> γ \gamma </math>γ | 折扣因子(论文中 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ = 0.99 \gamma=0.99 </math>γ=0.99) | 确保无限时域累计奖励收敛 |
2.2 强化学习的离散时间步过程
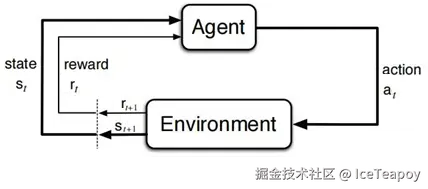
(1)状态观测
- 环境向智能体呈现当前状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s t ∈ S s_t \in \mathcal{S} </math>st∈S
- 状态是环境内部情况的完全或部分可观测表示
(2)动作选择
- 智能体根据内部策略生成动作 <math xmlns="http://www.w3.org/1998/Math/MathML"> a t ∈ A ( s t ) a_t \in \mathcal{A}(s_t) </math>at∈A(st)
- <math xmlns="http://www.w3.org/1998/Math/MathML"> A ( s t ) \mathcal{A}(s_t) </math>A(st) 表示状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s t s_t </math>st 下的可用动作集
(3)环境交互
- 动作 <math xmlns="http://www.w3.org/1998/Math/MathML"> a t a_t </math>at 被传递至环境
- 环境根据内部动态特性产生:
- 新状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s t + 1 ∼ P ( ⋅ ∣ s t , a t ) s_{t+1} \sim P(\cdot|s_t,a_t) </math>st+1∼P(⋅∣st,at)
- 即时标量奖励 <math xmlns="http://www.w3.org/1998/Math/MathML"> r t + 1 ∈ R r_{t+1} \in \mathbb{R} </math>rt+1∈R
(4)信息传递
- 环境向智能体返回:
- 下一状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s t + 1 s_{t+1} </math>st+1
- 奖励信号 <math xmlns="http://www.w3.org/1998/Math/MathML"> r t + 1 r_{t+1} </math>rt+1
- 终止标志 <math xmlns="http://www.w3.org/1998/Math/MathML"> d t + 1 ∈ { T r u e , F a l s e } d_{t+1} \in \{True, False\} </math>dt+1∈{True,False}
(5)时间步推进
- 系统时钟从 t 递进到 t+1
- 若 <math xmlns="http://www.w3.org/1998/Math/MathML"> d t + 1 = T r u e d_{t+1}=True </math>dt+1=True,当前回合终止并重置环境
- 否则继续新一轮状态观测
3 Q-Learning 算法
智能体的决策是怎样产生的呢?
传统方法是提前制定固定规则(如棋类套路),或者将整个环境建模预处理最优解。像考试前背下所有题目答案,但遇到新题就会失败。
Q-Learning的突破在于:放弃对环境的完美认知,转而从实际经验中学习。这种设计让它能应对现实世界中的不确定性,但也需要更多试错数据(类似人类需要多次练习才能掌握技能)。
3.1 评价函数
我们在面临一个状态 <math xmlns="http://www.w3.org/1998/Math/MathML"> s s </math>s 的时候,怎样评价在该状态下执行操作 <math xmlns="http://www.w3.org/1998/Math/MathML"> a a </math>a 的好坏呢?要回答这个问题,我们需要建立一个能够同时考虑即时收益和长期影响的评价标准。由于强化学习任务中奖励的稀疏性和延时性,这个标准不仅要反映当前动作带来的直接回报,还要包含这个动作对未来可能状态的潜在影响。
比如《打砖块》游戏中,当球从右侧飞来时,智能体需要决定是将球拍向左移动还是向右移动。单次操作使球拍移动的距离可能很小,无法带来任何收益。此外,还应该考虑这个动作会导致球飞向哪个方向,进而影响后续能否连续击碎更多砖块。
为此,首先定义累计回报 <math xmlns="http://www.w3.org/1998/Math/MathML"> G t G_t </math>Gt ------ 它表示从时刻 <math xmlns="http://www.w3.org/1998/Math/MathML"> t t </math>t 开始,未来所有奖励经过时间衰减后的总和:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + ⋯ = ∑ k = 0 ∞ γ k r t + k + 1 = r t + 1 + γ G t + 1 \begin{aligned} G_t &= r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots \\ &= \sum_{k=0}^\infty \gamma^k r_{t+k+1}\\ &= r_{t+1} + \gamma G_{t+1} \end{aligned} </math>Gt=rt+1+γrt+2+γ2rt+3+⋯=k=0∑∞γkrt+k+1=rt+1+γGt+1
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ ∈ [ 0 , 1 ) \gamma \in [0,1) </math>γ∈[0,1) 是折扣因子。这个设计既保证无穷级数收敛(当 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ < 1 \gamma<1 </math>γ<1时),又体现"近期奖励比远期更重要"的决策直觉。
首先考虑一个固定策略 π 的情况。假设我们有一个固定的行为规则,那么可以定义策略 π 下的动作价值函数:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Q π ( s , a ) = E π [ G t ∣ s t = s , a t = a ] Q^π(s,a) = \mathbb{E}_π \left[ G_t \mid s_t=s, a_t=a \right] </math>Qπ(s,a)=Eπ[Gt∣st=s,at=a]
这个函数表示在状态 s 下执行动作 a 后,继续按照策略 π 行动所能获得的期望累计回报。这里的期望是对策略 π 下所有可能轨迹的平均,就像记录一个固定打法的玩家千万次游戏的平均得分。
强化学习的目标是找到最优策略 π*,即在每个状态都能做出最佳决策的策略。这就引出了最优动作价值函数的概念:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Q ∗ ( s , a ) = max π Q π ( s , a ) Q^*(s,a) = \max_π Q^π(s,a) </math>Q∗(s,a)=πmaxQπ(s,a)
这个函数表示在所有可能的策略中,能够获得最大期望回报的那个策略对应的价值。理解这个区别很关键: <math xmlns="http://www.w3.org/1998/Math/MathML"> Q π Q^π </math>Qπ 反映的是特定策略的表现,而 <math xmlns="http://www.w3.org/1998/Math/MathML"> Q ∗ Q^* </math>Q∗ 反映的是潜在的最佳表现。
最优 <math xmlns="http://www.w3.org/1998/Math/MathML"> Q Q </math>Q 函数满足贝尔曼最优方程:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Q ∗ ( s , a ) = E [ r + γ max a ′ Q ∗ ( s ′ , a ′ ) ] Q^*(s,a) = \mathbb{E} \left[ r + \gamma \max_{a'} Q^*(s',a') \right] </math>Q∗(s,a)=E[r+γa′maxQ∗(s′,a′)]
该方程将一个全局优化问题转化为局部递归关系。右边的 <math xmlns="http://www.w3.org/1998/Math/MathML"> m a x max </math>max 操作确保了我们在每个后续状态都会选择最优动作,从而保证整个策略的最优性。方程本质反映了动态规划的最优子结构特性:当前最优决策必须包含后续所有最优决策。
如果我们对贝尔曼方程进行递归预处理,提前求出 <math xmlns="http://www.w3.org/1998/Math/MathML"> Q Q </math>Q 表,就回归到了传统方法。面临着状态空间巨大、需要提前得知环境信息和无法应对环境改变等问题。
3.2 迭代规则
实践中,我们无法遍历所有可能的未来路径,于是通过采样单次转移 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( s , a , r , s ′ ) (s,a,r,s') </math>(s,a,r,s′) 构造迭代规则:
Q-Learning 的迭代规则是:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Q ( s , a ) ← Q ( s , a ) + α ( r + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ) Q(s,a) \leftarrow Q(s,a) + \alpha \left( r + \gamma \max_{a'} Q(s',a') - Q(s,a) \right) </math>Q(s,a)←Q(s,a)+α(r+γa′maxQ(s′,a′)−Q(s,a))
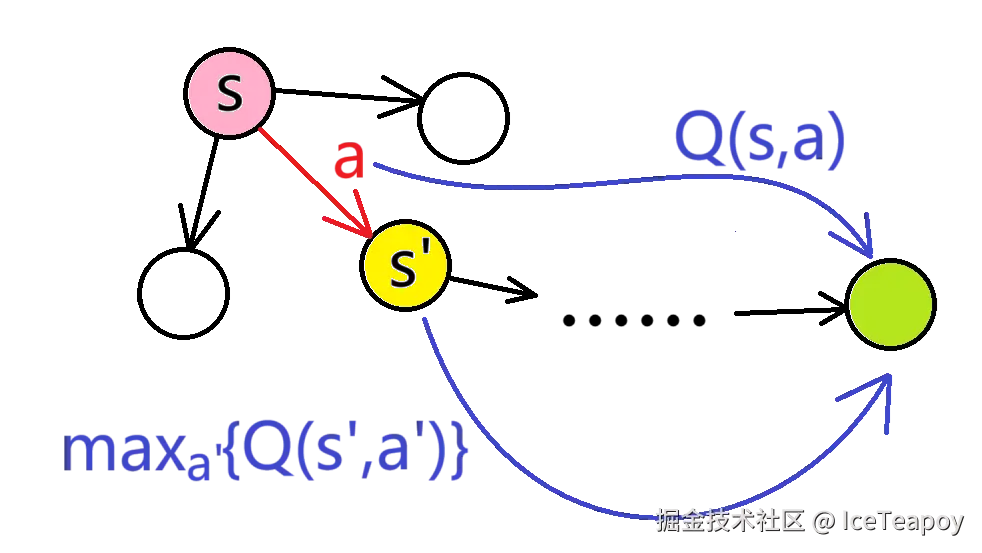
即将 <math xmlns="http://www.w3.org/1998/Math/MathML"> Q ( s , a ) Q(s,a) </math>Q(s,a) 更新为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Q ( s , a ) Q(s,a) </math>Q(s,a) 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> r + γ max a ′ Q ( s ′ , a ′ ) r + \gamma \max_{a'} Q(s',a') </math>r+γmaxa′Q(s′,a′) 的加权平均数。
经过充分迭代后, <math xmlns="http://www.w3.org/1998/Math/MathML"> Q Q </math>Q 函数最终收敛到真实的最优价值评估。
这为后续 DQN 的发展奠定基础------用深度网络拟合 Q 函数。这种"从试错中建立价值认知"的范式,成为现代强化学习的核心方法论。