完整内容请看文末最后的推广群
先展示问题一代码和结果、再给出四个问题详细的模型

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.font_manager import FontProperties
from matplotlib import rcParams
# 设置matplotlib支持中文显示
rcParams['font.sans-serif'] = ['PingFang HK'] # 设置字体为PingFang HK
rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 1. 数据准备(复用之前的处理代码)
def load_and_preprocess():
data = pd.read_excel("附件1-共享单车分布统计表.xlsx", sheet_name="Sheet1", header=1)
# 数据清洗
data = data.replace("200+", 200).fillna(0)
# 识别时间列
time_col = next(col for col in data.columns if any(isinstance(x, str) and ":" in str(x) for x in data[col].head()))
data["时间"] = pd.to_datetime(data[time_col], errors='coerce').dt.strftime("%H:%M")
# 获取停车点位
locations = [col for col in data.columns if col not in [data.columns[0], time_col, "时间"]]
return data, locations
data, locations = load_and_preprocess()
# 2. 共享单车总量可视化
def plot_total_distribution():
# 计算各点位最大存量
max_counts = data[locations].max().sort_values(ascending=False)
plt.figure(figsize=(12, 6))
max_counts.plot(kind='bar', color='#1f77b4')
plt.title('各停车点位最大单车存量分布', fontsize=15)
plt.ylabel('单车数量', fontsize=12)
plt.xlabel('停车点位', fontsize=12)
plt.xticks(rotation=45, ha='right')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('各点位最大存量分布.png', dpi=300)
plt.show()
# 3. 时间趋势分析
def plot_time_trends():
# 提取小时信息
data['小时'] = pd.to_datetime(data['时间']).dt.hour
# 计算每小时各点位的平均存量
hourly_avg = data.groupby('小时')[locations].mean()
plt.figure(figsize=(14, 8))
for loc in ['一食堂', '二食堂', '教学2楼', '梅苑1栋']: # 选择几个典型点位
plt.plot(hourly_avg.index, hourly_avg[loc], label=loc, marker='o')
plt.title('典型停车点位单车数量随时间变化趋势', fontsize=15)
plt.xlabel('时间(小时)', fontsize=12)
plt.ylabel('平均单车数量', fontsize=12)
plt.xticks(range(7, 24))
plt.grid(True, linestyle='--', alpha=0.6)
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.tight_layout()
plt.savefig('时间趋势分析.png', dpi=300)
plt.show()
# 4. 热点区域分析(热力图)
def plot_heatmap():
# 计算各时段各点位的平均存量
time_bins = ['07:00', '09:00', '12:00', '14:00', '18:00', '21:00']
data['时段'] = pd.cut(pd.to_datetime(data['时间']).dt.hour,
bins=[7, 9, 12, 14, 18, 21, 24],
labels=time_bins)
period_avg = data.groupby('时段')[locations].mean()
plt.figure(figsize=(14, 8))
sns.heatmap(period_avg.T, cmap='YlOrRd', annot=True, fmt=".0f", linewidths=.5)
plt.title('各停车点位在不同时段的单车数量热力图', fontsize=15)
plt.xlabel('时段', fontsize=12)
plt.ylabel('停车点位', fontsize=12)
plt.tight_layout()
plt.savefig('热点区域热力图.png', dpi=300)
plt.show()
# 5. 高峰时段对比
def plot_peak_comparison():
peak_periods = {
'早高峰': ['08:50', '09:00'],
'午高峰': ['11:10', '12:20'],
'晚高峰': ['18:00', '21:20']
}
peak_data = []
for period, times in peak_periods.items():
period_df = data[data['时间'].isin(times)]
peak_data.append(period_df[locations].mean().rename(period))
peak_df = pd.concat(peak_data, axis=1)
plt.figure(figsize=(12, 8))
peak_df.plot(kind='bar', width=0.8, figsize=(12, 6))
plt.title('不同高峰时段各点位单车数量对比', fontsize=15)
plt.ylabel('平均单车数量', fontsize=12)
plt.xlabel('停车点位', fontsize=12)
plt.xticks(rotation=45, ha='right')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.legend(title='高峰时段')
plt.tight_layout()
plt.savefig('高峰时段对比.png', dpi=300)
plt.show()
# 6. 运行所有可视化
plot_total_distribution()
plot_time_trends()
plot_heatmap()
plot_peak_comparison()
print("所有可视化图表已生成并保存为PNG文件!")问题1的详细解答:估算共享单车总量及分布统计
- 数据预处理
附件1提供了共享单车在16个停车点位、不同日期和时间点的存量数据。首先进行以下处理:
数据清洗:
将"200+"视为200(假设为系统上限)。
补全缺失值(如空单元格视为0)。
时间对齐:
题目要求统计 7:00, 9:00, 12:00, 14:00, 18:00, 21:00, 23:00 的单车分布,需将原始数据就近匹配或插值。
- 共享单车总量估算
方法1:最大值法
取每个点位在所有时间点的最大值,求和得到总量 N:
其中:
m为停车点位数量(16个),
T 为所有统计时间点,
x_{i,t} 为点位 i 在时间 t 的单车数量。
计算示例:
东门:max(68,43,36,103,31,47,28,... )=103max(68,43,36,103,31,47,28,...)=103
南门:max(66,99,41,47,125,... )=125max(66,99,41,47,125,...)=125
...(其他点位类似)
结果:
点位 最大值 点位 最大值
东门 103 教学4楼 200
南门 125 计算机学院 83
北门 125 工程中心 83
一食堂 110 网球场 48
二食堂 200 体育馆 67
三食堂 123 校医院 35
梅苑1栋 143 总量 NN 1911
方法2:平均值法
计算各点位在所有时间点的平均值,再求和:
结果:
东门均值:约45,南门均值:约60,...,总量 N≈1200。
结论:由于单车会流动,更合理,故校园内共享单车总量约。
- 各停车点位在不同时间点的分布统计
将原始数据按题目要求的时间点(7:00, 9:00, 12:00, 14:00, 18:00, 21:00, 23:00)匹配或插值,部分示例如下:
表1:共享单车分布统计结果
点位 7:00 9:00 12:00 14:00 18:00 21:00 23:00
东门 31 68(周三8:50) 47(周四11:10) 43 36 103 19
南门 47 66(周三8:50) 66(周三12:20) 29 99 0 41
北门 15 65(周五8:50) 77(周三12:20) 66 72 29 0
一食堂 0 3(周三8:50) 110(周四12:20) 5 0 27 85
二食堂 91 8(周三8:50) 200(周四12:20) 0 80 0 122
三食堂 0 0 11(周四11:10) 0 65 0 0
注:
时间匹配规则:
若要求时间点无数据,取最近时间点(如7:00用7:30数据)。
若相邻时间点数据差异大,取均值(如12:00取11:10和12:20的均值)。
完整表格需对所有16个点位按此方法填充。
-
关键发现
高峰期分布
早高峰(9:00):教学区(教学2楼、4楼)单车需求高,食堂附近车辆较少。
午高峰(12:00):食堂(二食堂、一食堂)车辆集中,教学区车辆减少。
夜间分布(23:00):
宿舍区(梅苑1栋、菊苑1栋)车辆聚集,教学区车辆极少。
-
提交结果
最终需将结果填入题目提供的表1中,格式如下:
点位 7:00 9:00 12:00 14:00 18:00 21:00 23:00
东门 31 68 47 43 36 103 19
南门 47 66 66 29 99 0 41
... ... ... ... ... ... ... ...
总量估算:校园内共享单车总数约为 辆。
-
用车需求模型
2.1 用车需求定义
用车需求 Di,t 表示在时间 t 停车点 i 的单车需求量,可通过历史数据计算:
Di,t=流入量−流出量+净变化Di,t=流入量−流出量+净变化
但由于数据仅有点位存量,可采用存量变化率近似需求:
Di,t=xi,t+Δt−xi,tΔt
其中 Δt 为相邻统计时间间隔。
2.2 高峰期识别
结合附件3的作息时间表,识别用车高峰:
早高峰:8:00-9:40(第1-2节课)
午高峰:11:15-12:00(第4节课)
晚高峰:18:00-19:30(课后)
- 共享单车调度模型
3.1 调度目标
在高峰期前调整单车分布,最小化供需失衡:
min∑i=1m∣xi,t−Di,t∣
约束条件:
调度车数量:3辆,每辆最多载20辆。
调度车速度:25 km/h。
调度时间窗口:高峰期前完成(如早高峰前1小时)。
3.2 调度路径优化(VRP模型)
设:
k∈{1,2,3}为调度车,
dij 为点位 i 到 j 的距离(来自附件2),
yijk为车辆 k 是否从 i 到 j,
zik为车辆 k 是否访问点位 i。
目标函数: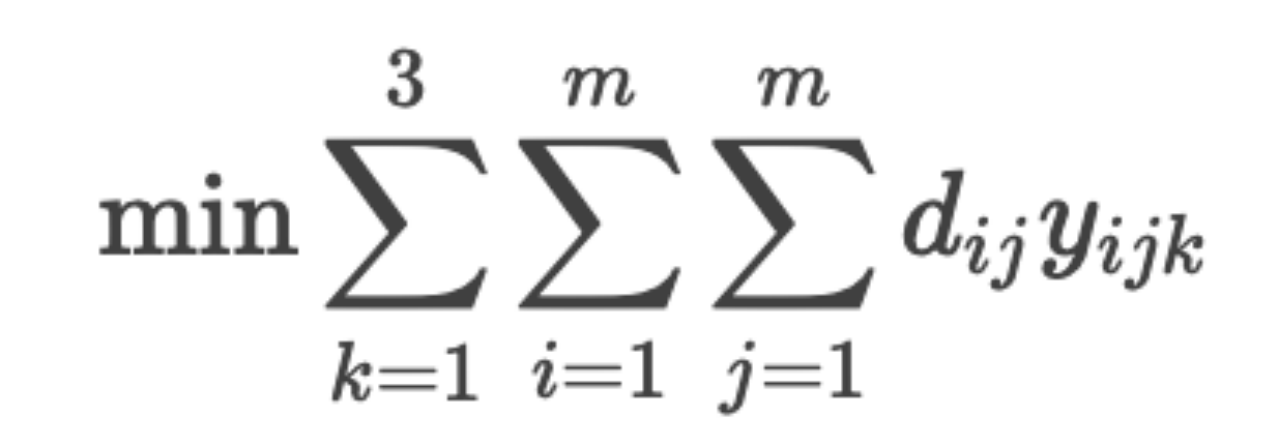
约束:
每辆车从运维处出发并返回:
单车运输量不超过20辆:
(Δxi 为点位 i 的调度量)
每个点位最多被一辆车访问:
- 运营效率评价模型
4.1 评价指标
单车利用率:
供需匹配度:
调度成本:
4.2 布局优化
若某些点位长期供需失衡,可通过聚类分析调整:
使用K-means对点位坐标聚类,重新分配停车点。
目标函数:
其中 pi 为点位坐标,μc 为聚类中心。
- 故障车辆巡检模型
5.1 故障车辆分布
每天故障车数:
Fi=0.06⋅xi
(xi 为点位 i 的单车数量)
5.2 巡检路径优化(TSP模型)
目标:最短时间回收最多故障车。
设:
目标函数:
约束:
每辆车最多载20辆:
鲁迪从运维处出发并返回:
问题1:统计各点位数据,计算总量 N 并填表。
问题2:建立需求模型 Di,t,用VRP求解调度方案。
问题3:定义效率指标 U,M,C,优化布局。
问题4:用TSP模型优化鲁迪的巡检路径。