数据结构--AVL树

1、基本概念

AVL 树是一种自平衡二叉搜索树。

• 定义：AVL 树是一种高度平衡的二叉搜索树，它在满足二叉搜索树性质的基础上，通过自动调整树的结构，确保树的高度在任何时候都保持在对数级别，从而保证了高效的查找、插入和删除操作。AVL 树得名于其发明者 G. M. Adelson - Velsky 和 E. M. Landis。

• 平衡因子：这是 AVL 树的一个关键概念。对于树中的每个节点，其平衡因子定义为该节点的右子树高度减去左子树高度（左子树减去右子树也可以）。在 AVL 树中，所有节点的平衡因子只能是 - 1、0 或 1。如果某个节点的平衡因子超出了这个范围，就说明树失去了平衡，需要进行调整。

• 调整操作：当插入或删除节点导致 AVL 树失去平衡时，需要通过特定的旋转操作来恢复平衡。主要有四种旋转操作，分别是左旋、右旋、先左旋后右旋、先右旋后左旋。这些旋转操作会改变节点之间的连接关系，以调整树的高度和结构，使树重新达到平衡状态。

• 其基本结构如下：

  struct AVLTreeNode
  {
  	AVLTreeNode(const T& data = T())
  		: _pLeft(nullptr)
  		, _pRight(nullptr)
  		, _pParent(nullptr)
  		, _data(data)
  		, _bf(0)
  	{}
  
  	AVLTreeNode<T>* _pLeft;
  	AVLTreeNode<T>* _pRight;
  	AVLTreeNode<T>* _pParent;
  	T _data;
  	int _bf;   // 节点的平衡因子
  };

  图示如下：

• 

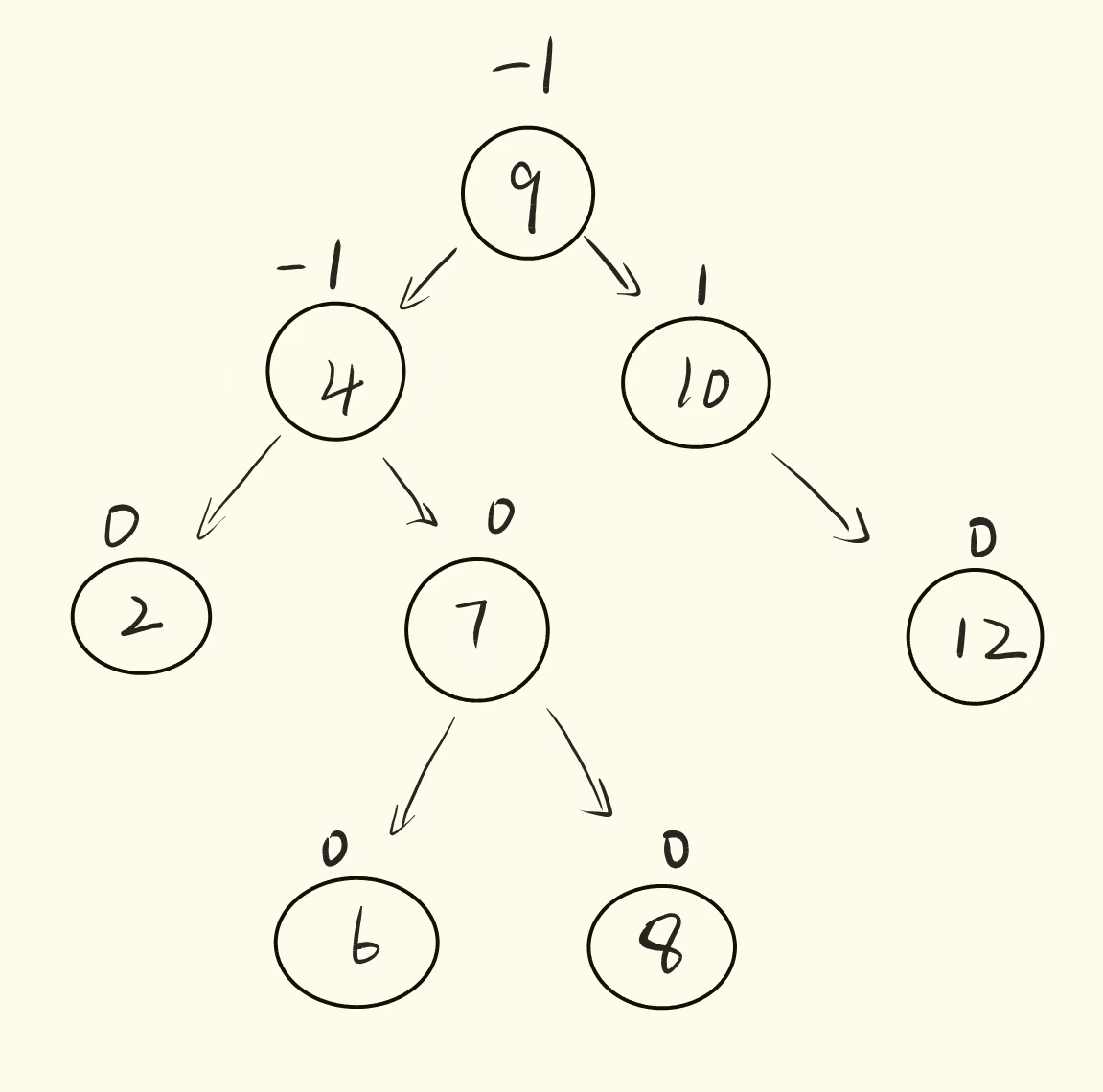
2、AVL树的插入（不允许重复插入）

AVL树的插入可以分作三个步骤:

步骤 1：按二叉搜索树规则插入新节点

• 从根节点开始，将新节点的值与当前节点的值进行比较。
• 如果新节点的值小于当前节点的值，则在当前节点的左子树中继续查找插入位置；如果新节点的值大于当前节点的值，则在当前节点的右子树中继续查找。
• 重复上述比较过程，直到找到一个空位置，将新节点插入该位置。

图示：

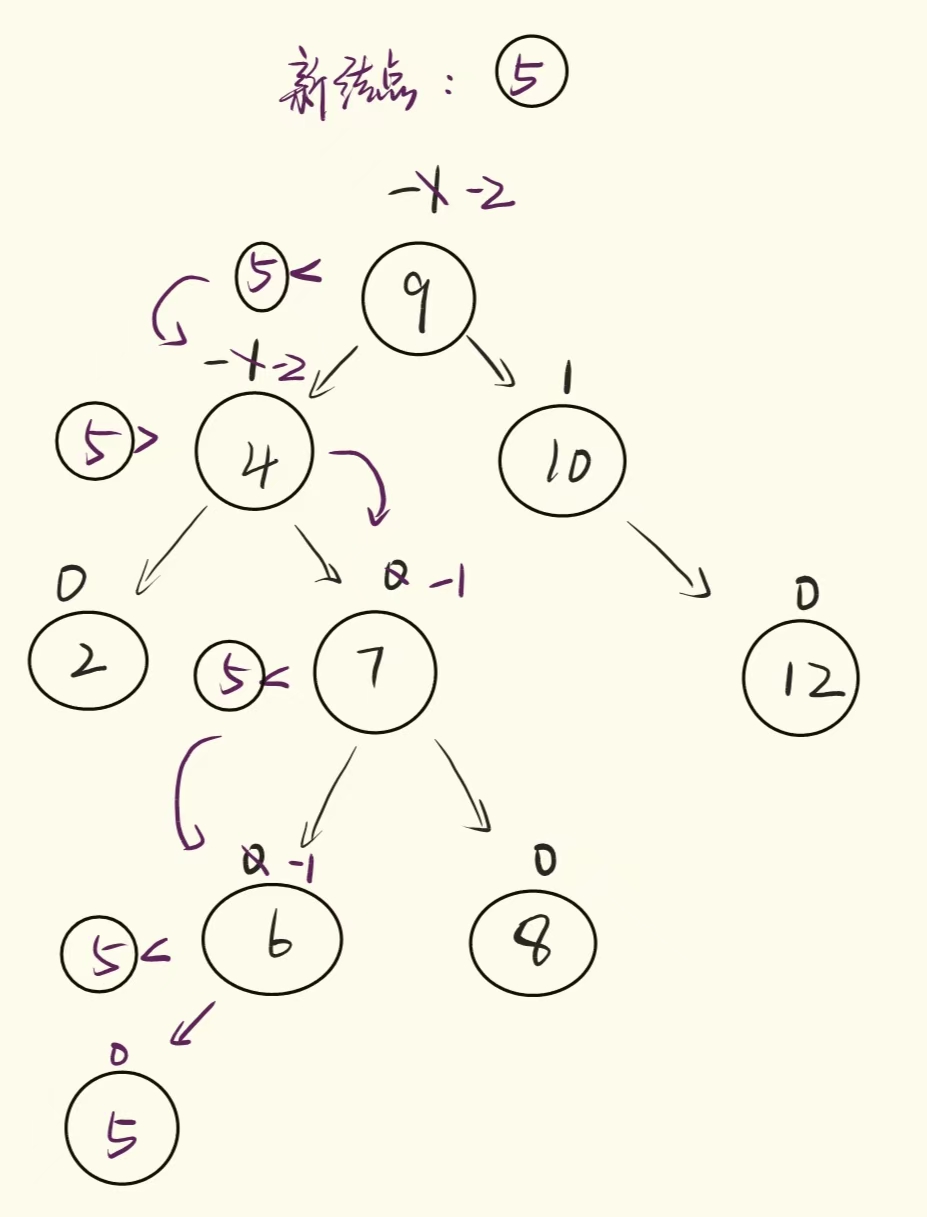
步骤 2：更新平衡因子并检查平衡

• 从插入的新节点开始，向上更新其所有祖先节点平衡因子。节点的平衡因子是该节点的右子树高度减去左子树高度。
• 如果某个节点的平衡因子的绝对值大于 1，说明 AVL 树的平衡被破坏，需要进行旋转操作来恢复平衡。

步骤 3：旋转操作恢复平衡

根据不平衡的情况，AVL 树有四种旋转操作：

其中需要注意的是，在左右双旋和右左双旋时，需要进行分类讨论，由于第一次单旋中其左/右子树平衡因子的不同，会导致最后平衡因子更新不同，有兴趣的可以动手试验一下。

LL（左左）旋转（右旋）：当某个节点的平衡因子为 2，且其左子节点的平衡因子为 1 时，需要进行右旋操作。

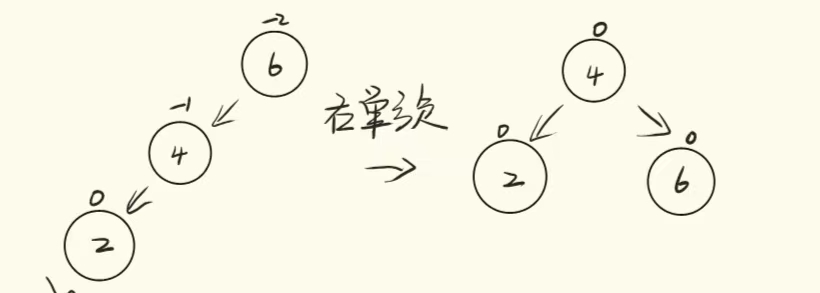
简单示例代码：

// 右单旋
void RotateR(Node* pParent)
{
//记录非法平衡因子节点的左子树及其左子树的右子树
	Node* subL = pParent->_pLeft;
	Node* subLR = subL->_pRight;

	pParent->_pLeft = subLR;
	if (subLR)
		subLR->_pParent = pParent;

	Node* p_parent = pParent->_pParent;
	subL->_pRight = pParent;
	pParent->_pParent = subL;
//不平衡节点为根节点
	if (p_parent  == nullptr)
	{
		_pRoot = subL;
		subL->_pParent = nullptr;
	}
	else
	{
		if (pParent == p_parent->_pLeft)
		{
			p_parent->_pLeft = subL;
		}
		else
		{
			p_parent->_pRight = subL;
		}
		subL->_pParent = p_parent;
	}
//更新平衡因子
	subL->_bf = 0;
	pParent->_bf = 0;
}

RR（右右）旋转（左旋）：当某个节点的平衡因子为 -2，且其右子节点的平衡因子为 -1 时，需要进行左旋操作。

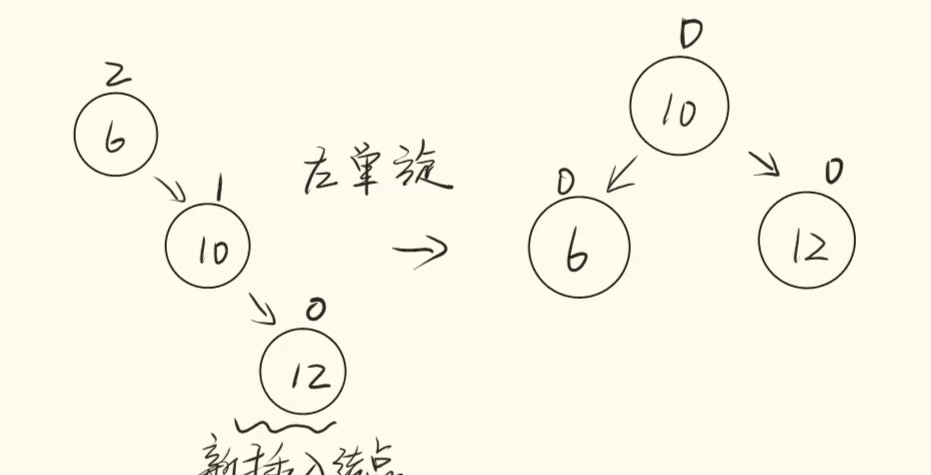
简单示例代码:

// 左单旋
void RotateL(Node* pParent)
{
	Node* subR = pParent->_pRight;
	Node* subRL = subR->_pLeft;

	pParent->_pRight = subRL;
	if (subRL)
		subRL->_pParent = pParent;

	Node* p_parent = pParent->_pParent;
	subR->_pLeft = pParent;
	pParent->_pParent = subR;
//不平衡节点为根节点
	if (p_parent == nullptr)
	{
		_pRoot = subR;
		subR->_pParent = nullptr;
	}
	else
	{
		if (pParent == p_parent->_pLeft)
		{
			p_parent->_pLeft = subR;
		}
		else
		{
			p_parent->_pRight = subR;
		}
		subR->_pParent = p_parent;
	}
//更新平衡因子
	subR->_bf = 0;
	pParent->_bf = 0;
}

LR（左右）旋转：当某个节点的平衡因子为 2，且其左子节点的平衡因子为 -1 时，先对左子节点进行左旋，再对该节点进行右旋。

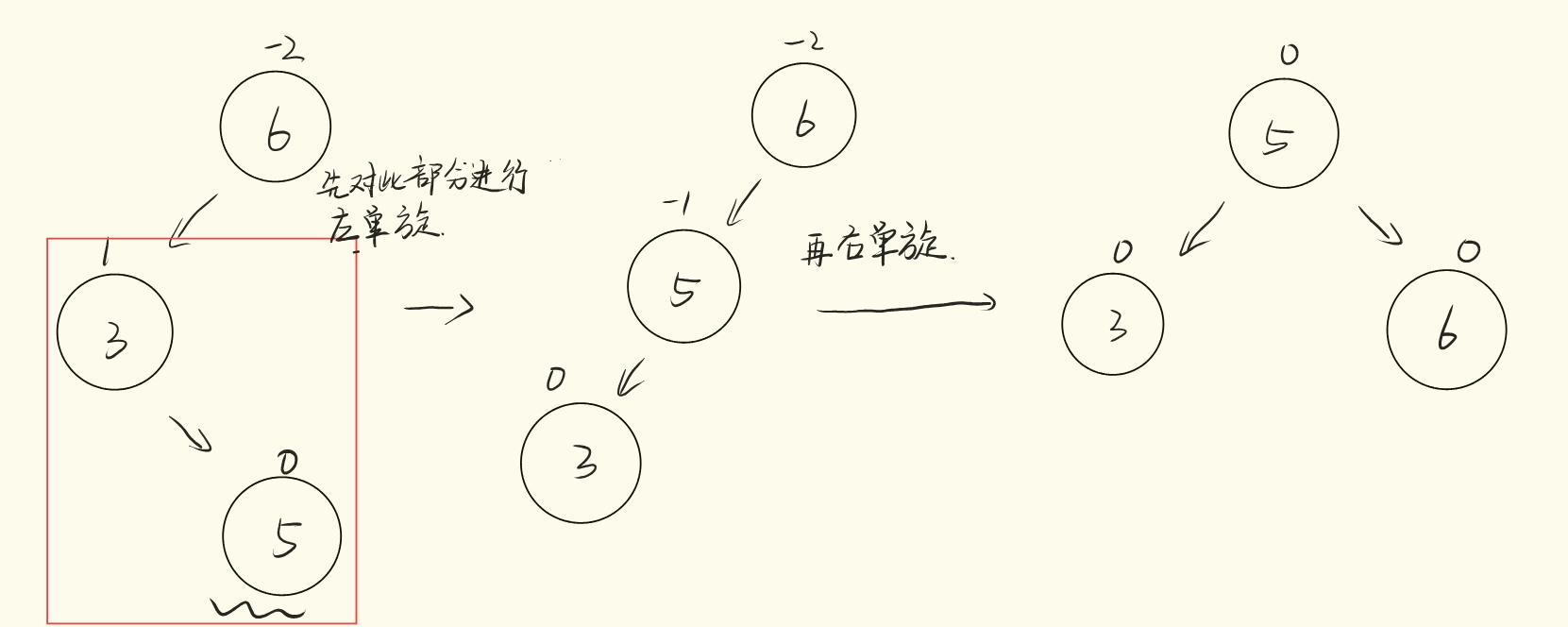
简单示例代码：

// 左右双旋
void RotateLR(Node* pParent)
{
	Node* subL = pParent->_pLeft;
	Node* subLR = subL->_pRight;

	int bf = subLR->_bf;
	RotateL(pParent->_pLeft);
	RotateR(pParent);
	//旋转后也有三种情况，需要分类讨论
	if (bf == 0)
	{
		subL->_bf = 0;
		subLR->_bf = 0;
		pParent->_bf = 0;
	}
	else if (bf == 1)
	{
		subL->_bf = -1;
		subLR->_bf = 0;
		pParent->_bf = 0;
	}
	else if (bf == -1)
	{
		subL->_bf = 0;
		subLR->_bf = 0;
		pParent->_bf = 1;
	}
	else
	{
		cout << "4" << endl;
		assert(false);
	}
}

RL（右左）旋转：当某个节点的平衡因子为 -2，且其右子节点的平衡因子为 1 时，先对右子节点进行右旋，再对该节点进行左旋。

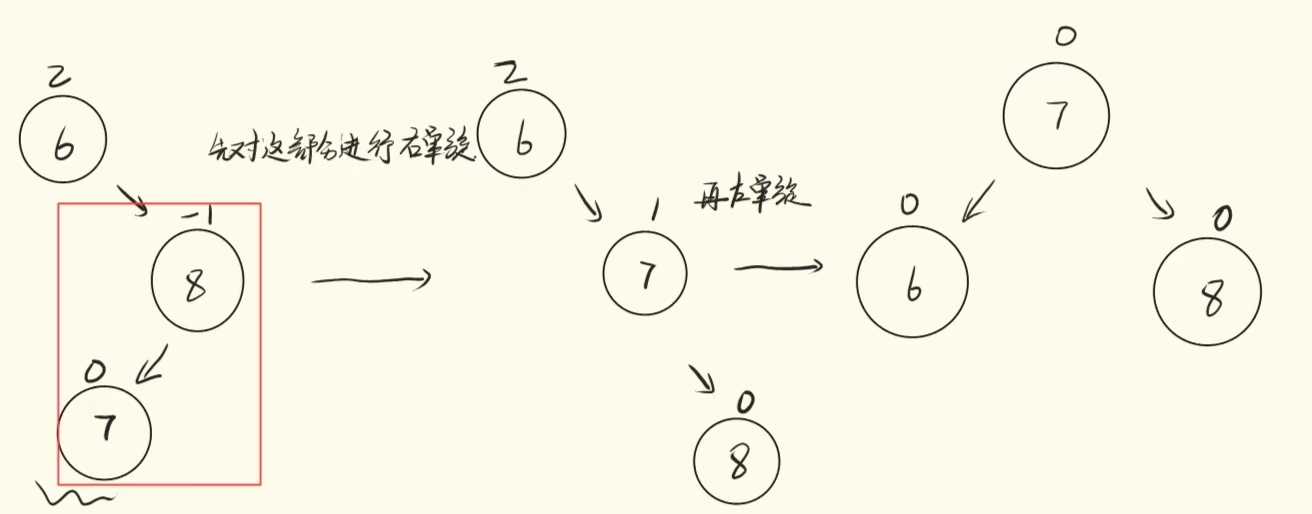
简单示例代码：

// 右左双旋
void RotateRL(Node* pParent)
{
	Node* subR = pParent->_pRight;
	Node* subRL = subR->_pLeft;

	int bf = subRL->_bf;
	RotateR(pParent->_pRight);
	RotateL(pParent);

	//一共有三种情况
	//bf = 1 -1 0
	//这三种情况旋转后的subR subRL pParent的bf会有变化
	if (bf == 0)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		pParent->_bf = 0;
	}
	else if (bf == 1)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		pParent->_bf = -1;
	}
	else if(bf == -1)
	{
		subR->_bf = 1;
		subRL->_bf = 0;
		pParent->_bf = 0;
	}
	else
	{
		cout << "3" << endl;
		assert(false);
	}
}

3.AVL树的查找

AVL 树本质上是一种二叉搜索树，所以其查找操作和普通二叉搜索树的查找操作基本一致。查找的核心思想是利用二叉搜索树的特性，即左子树所有节点的值小于根节点的值，右子树所有节点的值大于根节点的值，通过不断比较和递归或迭代的方式缩小查找范围，直到找到目标节点或者确定目标节点不存在。

查找步骤

1. 从根节点开始：将目标值与根节点的值进行比较。
2. 比较判断 ：
   • 如果目标值等于根节点的值，那么查找成功，返回该节点。
   • 如果目标值小于根节点的值，由于二叉搜索树的性质，目标节点只可能在左子树中，因此进入左子树继续查找。
   • 如果目标值大于根节点的值，目标节点只可能在右子树中，进入右子树继续查找。
3. 重复步骤 2：在子树中继续进行比较，不断缩小查找范围，直到找到目标节点或者到达空节点。
4. 查找失败：如果到达空节点还未找到目标值，说明目标值不在 AVL 树中，查找失败。

简单代码实现：

bool Find(const T& key)
{
	Node* cur = _pRoot;
	while (cur)
	{
		if (cur->_data < key)
		{
			cur = cur->_pRight;
		}
		else if (cur->_data > key)
		{
			cur = cur->_pLeft;
		}
		else
		{
			return true;
		}
	}

	return false;
}

4.AVL树的平衡检测

AVL 树的平衡性是其高效性能的保障，平衡性检查的目的是确保树中每个节点的平衡因子都在 -1 到 1 的范围内。如果某个节点的平衡因子超出这个范围，就需要通过旋转操作来恢复树的平衡。

平衡性检查步骤

1. 计算平衡因子：对于树中的每个节点，计算其平衡因子，平衡因子定义为左子树的高度减去右子树的高度。
2. 检查平衡因子范围：检查每个节点的平衡因子是否在 -1 到 1 的范围内。
3. 递归检查：对每个节点的左右子树也进行同样的平衡性检查。
4. 处理不平衡情况 ：如果发现某个节点的平衡因子超出了 -1 到 1 的范围，根据不平衡的类型（LL、RR、LR、RL）进行相应的旋转操作来恢复平衡。

简单代码示例：

// 根据AVL树的概念验证pRoot是否为有效的AVL树
bool _IsAVLTree(Node* pRoot)
{
	if (pRoot == nullptr)
		return true;
	int lh = _Height(pRoot->_pLeft);
	int rh = _Height(pRoot->_pRight);
	int diff = rh - lh;
	//左右子树高度差超过2
	if (abs(diff) >= 2)
	{
		cout << "高度差异常" << endl;
		return false;
	}
	//平衡因子与计算出的不同
	if (pRoot->_bf != diff)
	{
		cout << "平衡因子错误" << endl;
		return false;
	}
	//左右子树都是avl树，则该树是avl树
	return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
}