Three.js-硬要自学系列16 (贝塞尔曲线应用、组合曲线、路径管道、旋转成型、轮廓填充)

本章主要学习知识点

学习如何操作贝塞尔曲线控制点
掌握组合曲线CurvePath的使用
学习如何通过曲线路径创建管道
了解什么是旋转成型概念，并练习巩固
掌握如何通过轮廓填充一个面

贝塞尔曲线应用

通过上一章的学习，我们摘到二次贝塞尔曲线拥有一个控制点，三次则拥有两个控制点，在上一章中我们是直接将控制点写死，这一章中我们将通过代码来控制该控制点的变化

创建2个固定的坐标点，计算2点间的中心坐标点，然后将其作为控制点给到曲线

js 复制代码

const p1 = new THREE.Vector3(-10, 0, -10);
const p3 = new THREE.Vector3(10, 0, 10);
// 计算p1和p2的中点坐标
const x2 = (p1.x + p3.x)/2;
const z2 = (p1.z + p3.z)/2;
const p2 = new THREE.Vector3(x2, 15, z2);
const curve = new THREE.QuadraticBezierCurve3(p1, p2, p3);
const geometry = new THREE.BufferGeometry().setFromPoints(curve.getPoints(50))
const material = new THREE.LineBasicMaterial({color: 'deepskyblue'})
const curveObject = new THREE.Line(geometry,material)
scene.add(curveObject)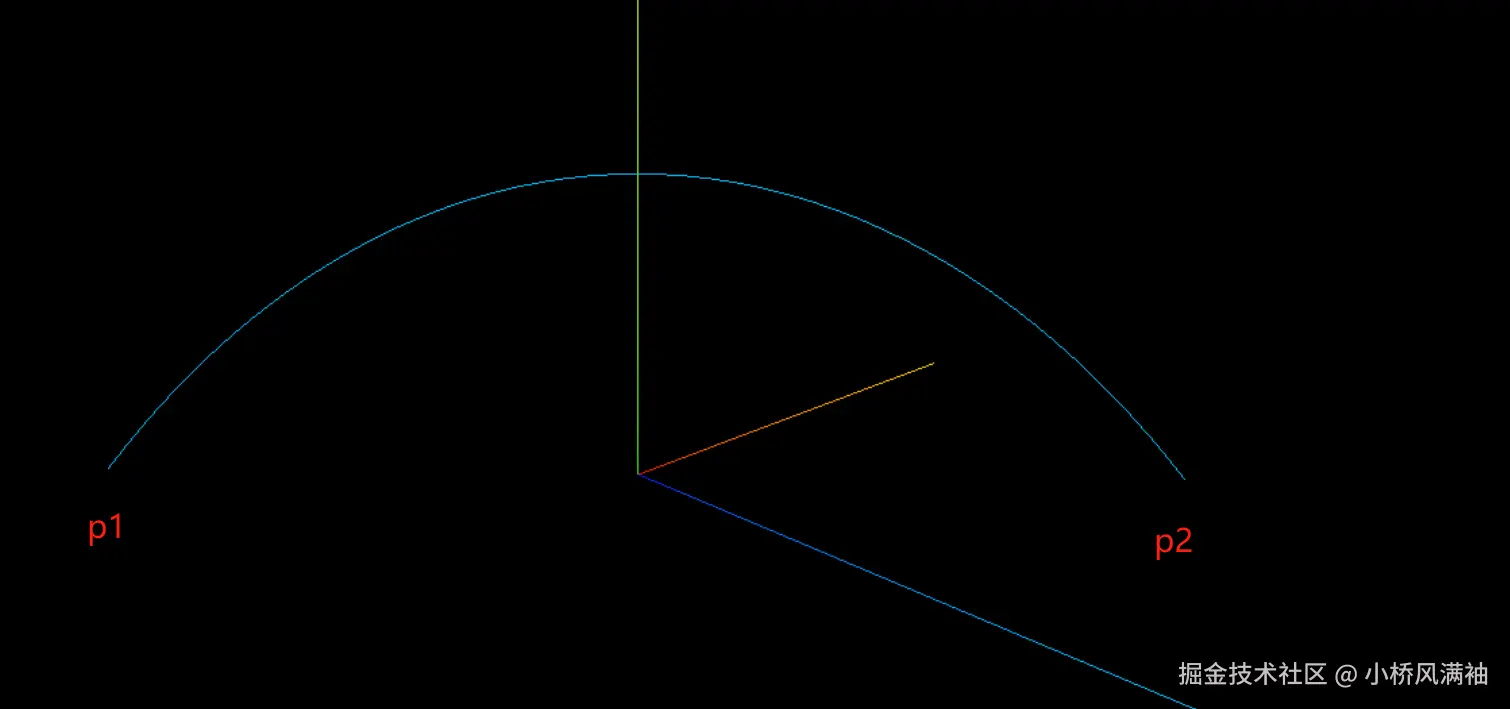

组合曲线 CurvePath

组合曲线就像用不同形状的积木拼出一条完整路径，我们可以把直线、圆弧、贝塞尔曲线等不同线段无缝连接成一个复杂的形状。

使用过程中需要注意每条曲线的终点必须是下一条曲线的起点，否则会出现断裂现象。

构建一个U型

要构建一个U型需要使用到两条直线和一条圆弧

js 复制代码

const R = 8;  // 圆弧半径
const H = 20; // 直线部分高度
const line1 = new THREE.LineCurve(new THREE.Vector2(R,H),new THREE.Vector2(R,0))
const line2 = new THREE.LineCurve(new THREE.Vector2(-R,0),new THREE.Vector2(-R,H))
const arc = new THREE.ArcCurve(0,0,R,0,Math.PI, true)

要组合管理这些线条需要使用到three.js中的 CurvePathAPI

js 复制代码

// 创建一个曲线路径
const curvePath = new THREE.CurvePath()
// 将直线1、弧线和直线2添加到曲线路径中
curvePath.curves.push(line1, arc, line2)
const geometry = new THREE.BufferGeometry().setFromPoints(curvePath.getPoints(50))
const material = new THREE.LineBasicMaterial({ color: 'skyblue' })
const curveObject = new THREE.Line(geometry, material)
// 将模型添加至场景中
scene.add(curveObject)

最终效果如下

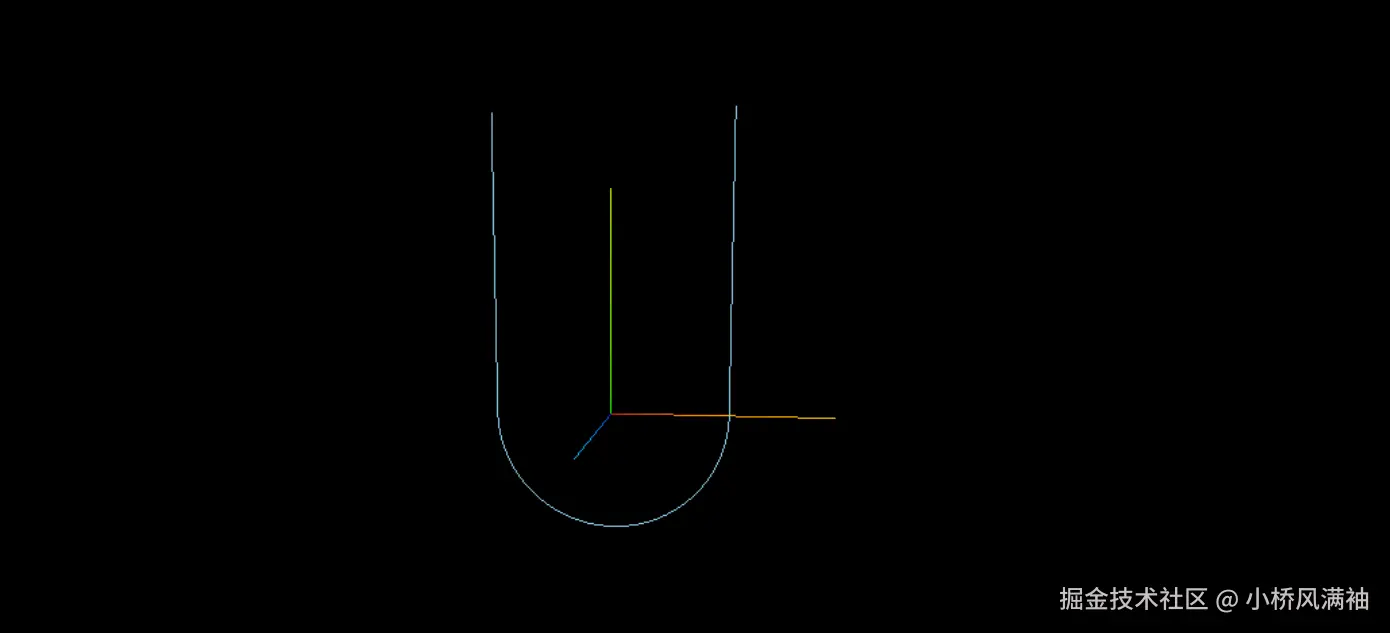
路径管道

路径管道是一种沿着自定义路径生成3D管状模型的技术，就像"用一根铁丝弯成任意形状，再裹上一层橡胶管"。

常见问题

管道内壁不可见 ：设置材质为双面渲染material.side = THREE.DoubleSide
管道断裂：检查路径控制点是否过于密集或间距过大
动画卡顿 ：减少动态管道的分段数或使用缓冲几何体（BufferGeometry)

使用场景

游戏场景：创建弯曲的隧道、滑梯轨道
数据可视化：模拟流体在管道中的流动（如血液、石油）
工业设计：展示机械管路的3D结构

实现一个简单的管道

通过组合曲线先实现线条的连接，然后调用TubeGeometry方法创建管道，该方法的第一个参数为曲线路径

js 复制代码

const p1 = new THREE.Vector3(0,0,10);
const p2 = new THREE.Vector3(0,0,3);
const p3 = new THREE.Vector3(0,0,0);
const p4 = new THREE.Vector3(3,0,0);
const p5 = new THREE.Vector3(10,0,0);
const line1 = new THREE.LineCurve3(p1,p2)
const curve = new THREE.QuadraticBezierCurve3(p2,p3,p4)
const line2 = new THREE.LineCurve3(p4,p5)

// 创建一个曲线路径
const CurvePath = new THREE.CurvePath();
// 将三条线添加到曲线路径中
CurvePath.curves.push(line1, curve, line2)

// 创建一个TubeGeometry对象，参数分别为CurvePath（曲线路径）、50（分段数）、1（半径）、30（径向分段数）
const geometry = new THREE.TubeGeometry(CurvePath, 50, 1, 30)
const material = new THREE.MeshLambertMaterial({color: 'deepskyblue',side: THREE.DoubleSide})
const mesh = new THREE.Mesh(geometry,material)
scene.add(mesh)

旋转成型

旋转成型（Lathe Geometry） 是一种通过二维轮廓线绕轴旋转生成三维模型的技术，类似于陶艺中的「拉坯」工艺。

你可以想象用剪刀剪出一个花瓶的侧面轮廓（如半圆形），然后让这个轮廓围绕中心轴快速旋转，最终形成一个立体的花瓶模型。

实践一下

js 复制代码

const pointsArr = [
    new THREE.Vector2(5,6),
    new THREE.Vector2(2.5,0),
    new THREE.Vector2(5,-6)
]

const geometry = new THREE.LatheGeometry(
    pointsArr,   // 轮廓线点数组
    50,  // 分段数（数值越大表面越平滑）
    0,   // 起始角度（默认0，即从正X轴开始）
    Math.PI*2)  // 结束角度（2π表示完整旋转一周）
const material = new THREE.MeshLambertMaterial({color: 'deepskyblue'})
const mesh = new THREE.Mesh(geometry,material)
scene.add(mesh)

这里使用了LatheGeometry,它用于将轮廓线绕Y轴旋转生成几何体

轮廓填充

轮廓填充可以理解为"用一组顶点坐标自动生成封闭区域的平面几何体"，就像用笔勾画一个多边形后，自动填充颜色使其变成实心图形。

定义轮廓顶点

将多边形的顶点坐标按顺序排列（顺时针或逆时针）

js 复制代码

const pointsArr = [
    new THREE.Vector2(-5,-5),
    new THREE.Vector2(-6,0),
    new THREE.Vector2(0,5),
    new THREE.Vector2(6,0),
    new THREE.Vector2(5,-5)
]

创建Shape对象

将这些顶点传入THREE.Shape，它会自动识别为一个封闭轮廓

js 复制代码

const shape = new THREE.Shape(pointsArr);

生成填充几何体

使用ShapeGeometry将轮廓转化为3D平面，内部自动计算三角形面片填充区域

js 复制代码

const geometry = new THREE.ShapeGeometry(shape);
const material = new THREE.MeshBasicMaterial({color: 'deepskyblue',side: THREE.DoubleSide})
const mesh = new THREE.Mesh(geometry,material)
scene.add(mesh)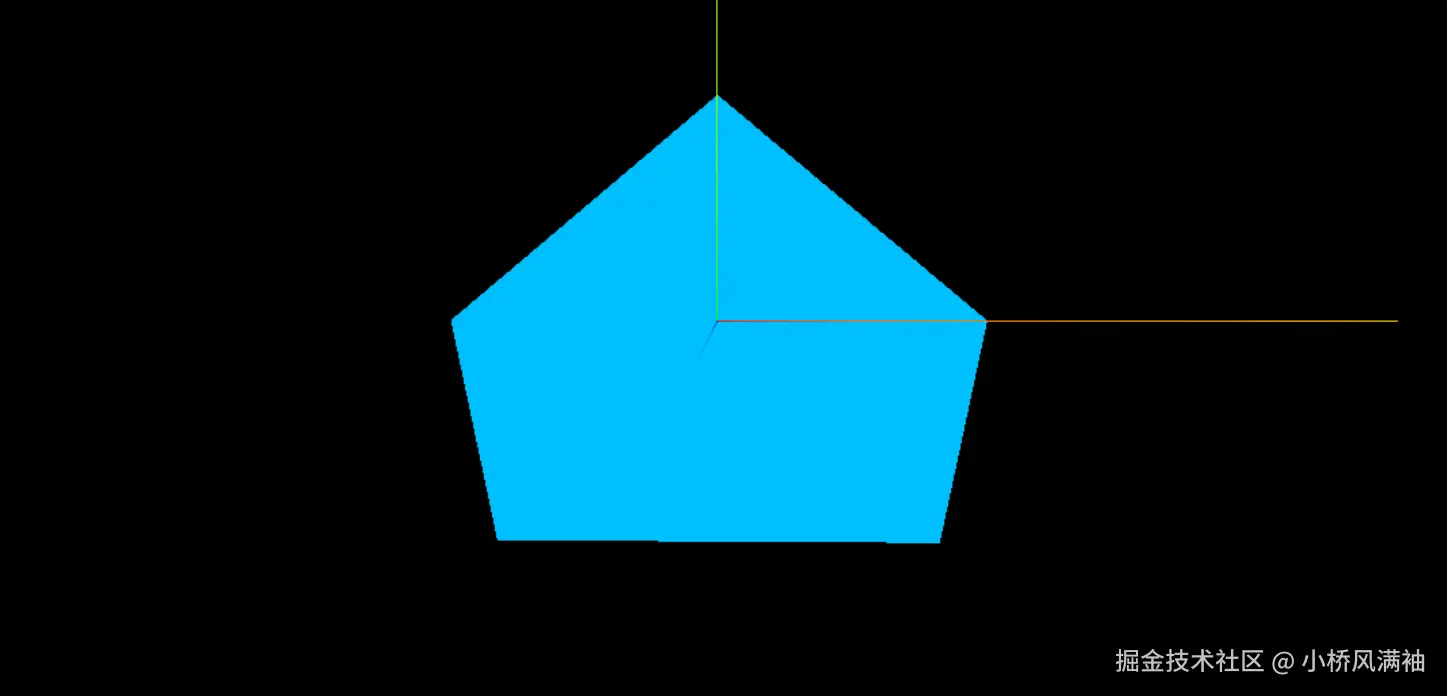

以上案例均可在案例中心查看体验

THREE 案例中心