机器学习-入门-决策树(1)

机器学习-入门-决策树(1)

4.1决策树的基本流程

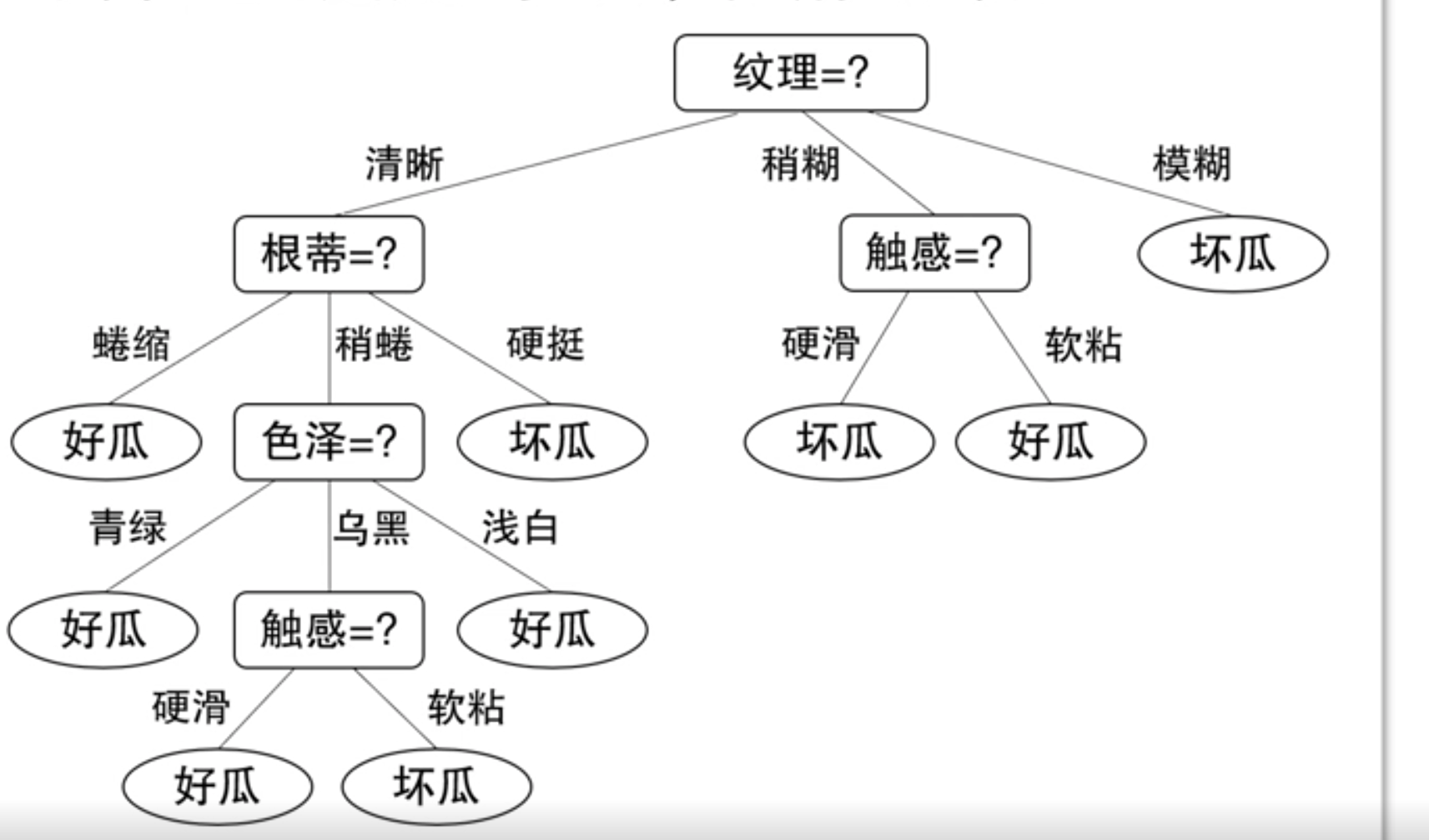
决策树基于"树"结构进行决策

• 每个"内部结点"对应于某个属性上的"测试"(test)
• 每个分支对应于该测试的一种可能结果（即该属性的某个取值）
• 每个"叶结点"对应于一个"预测结果"

学习过程：通过对训练样本的分析来确定"划分属性"（即内部结点所对应的属性）

预测过程：将测试示例从根结点开始，沿着划分属性所构成的"判定测试序列"下行，直到叶结点

策略："分而治之" (divide-and-conquer)

• 自根至叶的递归过程
• 在每个中间结点寻找一个"划分" (split or test) 属性

三种停止条件：

1. 当前结点包含的样本全属于同一类别，无需划分；
2. 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；
3. 当前结点包含的样本集合为空，不能划分。

基本算法

输入：

• 训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ... , ( x m , y m ) } D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_m, y_m)\} D={(x1,y1),(x2,y2),...,(xm,ym)}
• 属性集 A = { a 1 , a 2 , ... , a d } A = \{a_1, a_2, \ldots, a_d\} A={a1,a2,...,ad}

过程 ：函数 TreeGenerate ( D , A ) \text{TreeGenerate}(D, A) TreeGenerate(D,A)

1. 生成结点 node \text{node} node；
2. if D D D 中样本全属于同一类别 C C C then
   • 将 node \text{node} node 标记为 C C C 类叶结点；
   • return
3. end if
4. if A = ∅ A = \emptyset A=∅ OR D D D 中样本在 A A A 上取值相同 then
   • 将 node \text{node} node 标记为叶结点，其类别标记为 D D D 中样本数最多的类；
   • return
5. end if
6. 从 A A A 中选择最优划分属性 a ∗ a_{*} a∗；
7. for a ∗ a_{*} a∗ 的每一个值 a ∗ v a_{*}^v a∗v do
   • 为 node \text{node} node 生成一个分支；
   • 令 D v D_v Dv 表示 D D D 中在 a ∗ a_{*} a∗ 上取值为 a ∗ v a_{*}^v a∗v 的样本子集；
   • if D v D_v Dv 为空 then
     • 将分支结点标记为叶结点，其类别标记为 D D D 中样本最多的类；
     • return
   • else
     • 以 TreeGenerate ( D v , A ∖ { a ∗ } ) \text{TreeGenerate}(D_v, A \setminus \{a_{*}\}) TreeGenerate(Dv,A∖{a∗}) 为分支结点；
   • end if
8. end for

输出 ：以 node \text{node} node 为根结点的一棵决策树

4.2信息增益划分

信息熵 (Entropy)

信息熵是度量样本集合"纯度"最常用的指标。

定义 ：

对于样本集合 D D D，其中第 k k k 类样本所占比例为 p k p_k pk，信息熵定义为：
E n t ( D ) = − ∑ k = 1 ∣ Y ∣ p k log ⁡ 2 p k Ent(D) = -\sum_{k=1}^{|\mathcal{Y}|} p_k \log_2 p_k Ent(D)=−k=1∑∣Y∣pklog2pk

约定：

• 若 p k = 0 p_k = 0 pk=0，则 p k log ⁡ 2 p k = 0 p_k \log_2 p_k = 0 pklog2pk=0
• E n t ( D ) Ent(D) Ent(D) 的最小值为 0 0 0（完全纯净），最大值为 log ⁡ 2 ∣ Y ∣ \log_2 |\mathcal{Y}| log2∣Y∣（完全混乱）

性质：

• E n t ( D ) Ent(D) Ent(D) 值越小，集合 D D D 的纯度越高

信息增益 ：

基于信息熵计算当前划分对信息熵的变化，用于选择最优划分属性。

信息增益 (Information Gain)

定义 ：

对于离散属性 a a a 有 V V V 个取值 { a 1 , a 2 , ... , a V } \{a^1, a^2, \ldots, a^V\} {a1,a2,...,aV}，其信息增益公式为：
Gain ( D , a ) = Ent ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) \text{Gain}(D, a) = \text{Ent}(D) - \sum_{v=1}^V \frac{|D^v|}{|D|} \text{Ent}(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)

符号说明：

• D v D^v Dv： D D D 中在属性 a a a 上取值为 a v a^v av 的样本子集
• Ent ( D ) \text{Ent}(D) Ent(D)：划分前的信息熵（原始数据集纯度）
• ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) \sum_{v=1}^V \frac{|D^v|}{|D|} \text{Ent}(D^v) ∑v=1V∣D∣∣Dv∣Ent(Dv)：划分后的加权信息熵

关键点：

1. ∣ D v ∣ ∣ D ∣ \frac{|D^v|}{|D|} ∣D∣∣Dv∣ 是第 v v v 个分支的权重（样本越多，分支影响越大）
2. 直接采用信息增益作为属性划分标准
3. 信息增益越大，表示该属性划分带来的纯度提升越显著

4.3其他属性划分准则

信息增益的缺陷

• 对多值属性存在偏好：倾向于选择取值数目多的属性（如"编号"这类无意义属性）
• 示例：若将"编号"作为属性，因其唯一性会导致信息增益最大化，但实际无分类意义

增益率 (Gain Ratio)

定义 ：
Gain_ratio ( D , a ) = Gain ( D , a ) IV ( a ) \text{Gain\_ratio}(D,a) = \frac{\text{Gain}(D,a)}{\text{IV}(a)} Gain_ratio(D,a)=IV(a)Gain(D,a)

其中 固有值 (Intrinsic Value) 为：
IV ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log ⁡ 2 ∣ D v ∣ ∣ D ∣ \text{IV}(a) = -\sum_{v=1}^{V} \frac{|D^v|}{|D|} \log_2 \frac{|D^v|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣

关键性质：

1. IV ( a ) \text{IV}(a) IV(a) 反映属性 a a a 的取值分散程度：
   • 取值数目 V V V 越大， IV ( a ) \text{IV}(a) IV(a) 通常越大
2. 作用 ：通过除以 IV ( a ) \text{IV}(a) IV(a) 惩罚多值属性，缓解信息增益的偏好问题
3. C4.5算法：采用增益率作为属性划分标准

注意：增益率可能对取值较少的属性有偏好，实践中常先筛选信息增益高于平均的属性，再从中选增益率最大的。

基尼指数 (Gini Index)

基尼值的定义

数据集 D D D 的基尼值衡量从 D D D 中随机抽取两个样本其类别标记不一致的概率：
Gini ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 \text{Gini}(D) = \sum_{k=1}^{|\mathcal{Y}|} \sum_{k' \neq k} p_k p_{k'} = 1 - \sum_{k=1}^{|\mathcal{Y}|} p_k^2 Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2

性质：

• Gini ( D ) \text{Gini}(D) Gini(D) 越小，数据集 D D D 的纯度越高
• 取值范围： 0 0 0（完全纯净）到 1 − 1 ∣ Y ∣ 1-\frac{1}{|\mathcal{Y}|} 1−∣Y∣1（最大混乱）

属性 a a a 的基尼指数定义为各子集基尼值的加权和：
Gini_index ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Gini ( D v ) \text{Gini\index}(D,a) = \sum{v=1}^V \frac{|D^v|}{|D|} \text{Gini}(D^v) Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)

其中 D v D^v Dv 是 D D D 中属性 a a a 取值为 a v a^v av 的子集。

划分准则：

• 选择使划分后基尼指数最小的属性：
  a ∗ = a r g m i n a ∈ A Gini_index ( D , a ) a_* = argmin_{a \in A} \text{Gini\_index}(D,a) a∗=argmina∈AGini_index(D,a)

应用：

• CART算法（Classification and Regression Trees）采用基尼指数作为属性划分标准
• 对比信息增益/增益率：基尼指数计算更高效，且对多值属性敏感度较低

示例 ：

若属性 a a a 将 D D D 划分为 D 1 D_1 D1 和 D 2 D_2 D2，则基尼指数为：
Gini_index ( D , a ) = ∣ D 1 ∣ ∣ D ∣ Gini ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ Gini ( D 2 ) \text{Gini\_index}(D,a) = \frac{|D_1|}{|D|} \text{Gini}(D_1) + \frac{|D_2|}{|D|} \text{Gini}(D_2) Gini_index(D,a)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)

决策树泛化性能的关键因素

划分准则的影响

1. 对树结构的作用

   • 信息增益、增益率、基尼指数等划分标准会显著影响决策树的尺寸（深度、节点数）
   • 实际差异 ：不同准则产生的树仅在约 2% 的情况下存在划分差异

2. 对泛化性能的局限性

   • 划分准则的选择对模型最终泛化能力影响有限
   • 不同准则（如信息增益 vs 基尼指数）的泛化性能差异通常可忽略

剪枝的核心作用

1. 决定性影响

   • 剪枝方法（预剪枝/后剪枝）及剪枝程度对泛化性能的贡献远大于划分准则
   • 数据带噪时 ：合理剪枝可能将泛化性能提升高达 25%

2. 噪声数据的适应性

   • 剪枝能有效抑制过拟合，尤其在噪声较多或训练数据不足的场景中

实践建议

• 优先优化剪枝策略：而非过度纠结划分准则的选择
• 鲁棒性设计：在噪声环境中应强制启用剪枝机制