数据结构——树（中篇）

今日名言：

人生碌碌，竞短论长，却不道枯荣有数，得失难量

---

上次我们讲了树的相关知识，接下来就进一步了解二叉树吧。本文为个人学习笔记，如有侵权，请

联系删除，如有错误，欢迎批评指正！！！

上次讲到了建堆的做法，这次我们来讲讲有关堆的应用吧

堆排序

堆排序就是利用堆的思想来排序，总共分为两个步骤

---

1.建堆

• 升序：建大堆
• 降序：建小堆

这里可能有人有疑问，为什么升序是建大堆，而降序是建小堆呢？以小堆为例，我们建完小堆后，第一个元素就是最小的，那么为了得到第二小的元素我们就得继续建小堆，这样时间你复杂度就比较高；而如果我们利用堆删除的方法来排序，将第一个元素和最后一个元素交换，取最后一个元素，然后采用向下调整的方法调整，这样依次进行，就可以得到一个降序序列。

2.利用堆删除的方法进行排序

代码实现

for (int i = (n - 2) / 2;i >= 0;i--) {
	AdjustDown(a, n, i);
	int end = n - 1;//找到最后一个元素
	while (end > 0) {
		swap(&a[0], &a[end]);//交换第一个与最后一个
		AdjustDown(a, n, i);//向下调整
		end--;//排除最后一个继续调整
	}
}

图解：

Top-K问题

什么是TOP-K问题呢？

即是求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大，其实这类问题在我们的日常生活中十分常见，例如专业前十名，世界五百强等等。

对于这类问题，我们一般的方法就是排序，但是数据量大，排序可能就不适合了。

---

如果用堆来解决，我们有两种方法

• 方法一：在大堆中pop k次就能找到最大的前K个，在小队中pop k次就能找到最小的前K个。但是这种方法会有弊端，数据量大的时候就需要非常多的空间，这样内存可能不够用
• 方法二：如果是查找前K个最大的元素，我们就用前K个元素建小堆， 再用剩余的元素与堆顶元素比较，如果比堆顶元素大，就如替换堆顶元素；如果是查找前K个最小的元素，我们就用前K个元素见大堆，再用剩余的元素与堆顶元素比较，如果比堆顶元素小，则替换堆顶元素。

下面我们通过一道具体的题来体会一下

题目来源：面试题 17.14. 最小K个数 - 力扣（LeetCode）

题目描述：

代码解答：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
void AdjustDown(int*arr,int n,int root){
    int parent=root;
    int child=2*root+1;
    while(child<n){
        if(child+1<n&&arr[child]<arr[child+1]){//防止越界
            child++;//如果左孩子小于右孩子，那么就交换二者的值
        }
    if(arr[parent]<arr[child]){
        int t=arr[parent];
        arr[parent]=arr[child];
        arr[child]=t;//交换二者的值
    }
    parent=child;
    child=2*parent+1;//更新二者的值
    }
 }
int* smallestK(int* arr, int arrSize, int k, int* returnSize) {
    if(arrSize==0||k<=0){//如果数组大小为0或者前k个数小于等于0，那么返回的是空数组，且大小为0
        return NULL;
        *returnSize=0;
    }
    int *returnarr=(int*)malloc(sizeof(int)*k);
    int i=0;
    for(i=0;i<k;i++){
        returnarr[i]=arr[i];//将前K个数存入返回数组中
    }
    for(i=(k-2);i>=0;i--){
        AdjustDown(returnarr,k,i);//建大堆
    }
    for(i=k;i<arrSize;i++){//如果数组中剩余的值比堆顶元素小，则替换堆顶元素
        if(arr[i]<returnarr[0]){
            returnarr[0]=arr[i];
            AdjustDown(returnarr,k,0);
        }
    }
    *returnSize=k;
    return returnarr;

}

图解：

二叉树的遍历

学习二叉树结构，最简单的方式就是遍历，所谓二叉树的遍历就是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

---

按照规则，二叉树的遍历有：前序，中序，后序的递归结构遍历（这三种遍历是根据访问根的先后顺序进行划分的）

• 前序遍历（也叫做先序遍历）------访问根节点的操作发生在遍历其左右子树之前（根---左子树---右子树）
• 中序遍历------访问根节点的操作发生在遍历其左右子树之中（左子树---根---右子树）
• 后序遍历------访问根节点的操作发生在遍历其左右子树之后（左子树---右子树---根）

下面我们来看一个具体的例子，当然，在写他们的遍历时，可以省去NULL

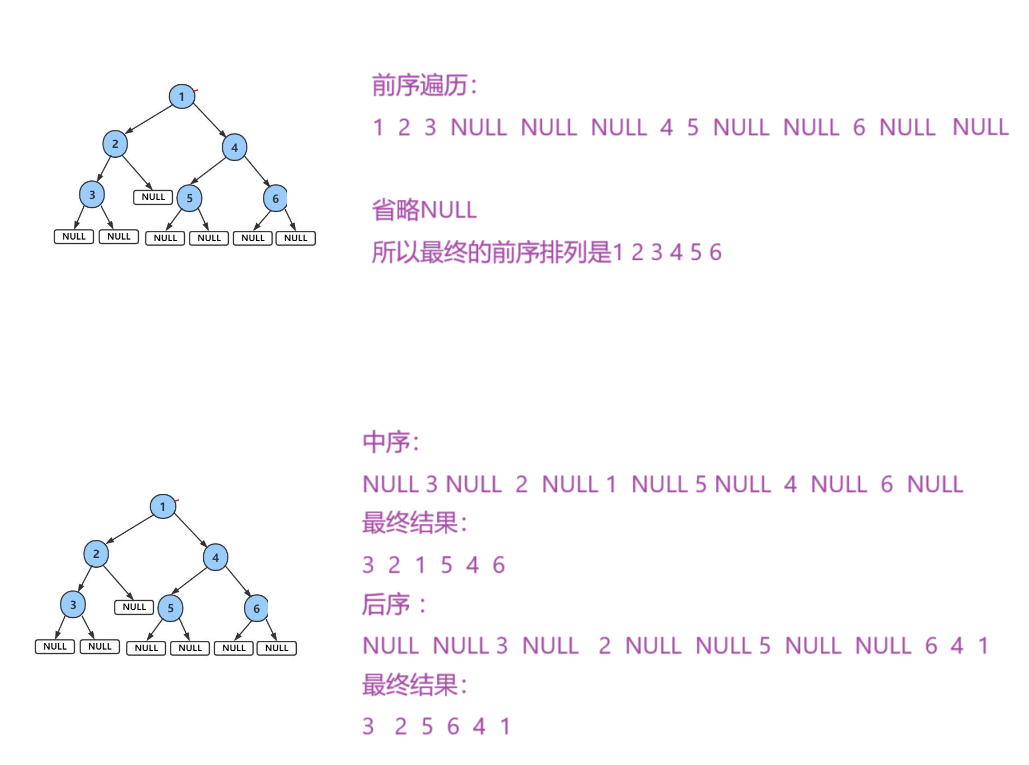
前序遍历的代码实现

void preorderTraversal(TreeNode* root) {
    if (root == NULL) {
        printf("NULL ");
    }
    if (root != NULL) {
        printf("%d ", root->val);
        preorderTraversal(root->left);
        preorderTraversal(root->right);
    }
}

后序遍历的代码实现

void postorderTraversal(TreeNode* root) {
    if (root == NULL) {
        printf("NULL ");
    }
    if (root != NULL) {
        postorderTraversal(root->left);
        postorderTraversal(root->right);
        printf("%d ", root->val);
    }
}

中序遍历的代码实现

void inorderTraversal(TreeNode* root) {
    if (root == NULL) {
        printf("NULL ");
    }
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->val);
        inorderTraversal(root->right);
    }
}

最终效果

层序排列：

除了以上三种遍历方法之外，还可以对二叉树进行层序遍历。假设二叉树根节点所在层数是1，那么层序遍历就是从根节点出发，首先访问第一层的节点，然后从左到右访问第二层上的节点，以此类推从上至下，从左往右逐层访问树的节点的过程就是层序遍历，也就是一层层遍历

当给定前序/后序+中序就能确定唯一的二叉树，而当给定前序+后序的话是不能确定唯一的二叉树的。

1.已知前序和后序

前序（根左右）：EFHIGJK、中序（左右根）：HFIEJKG

那么我们现在来判断二叉树

2.已知后序和中序

后序:bdeca,中序：badce;

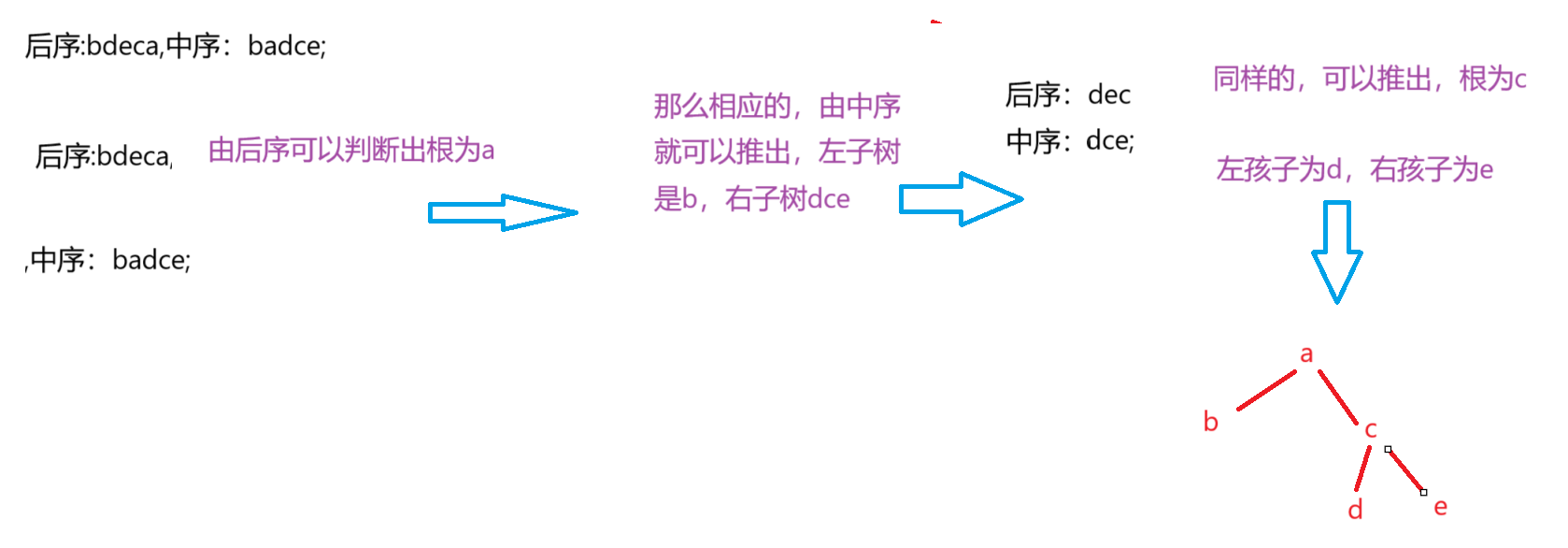
有关二叉树的一些题目

1.求二叉树中得的节点个数

代码实现

//方法一：与前中后序的遍历原理相同
int size = 0;//用全局变量来记录节点的个数
void BTreeSize1(BTNode* node) {
	if (node == NULL) {
		return;如果为空则直接返回
	}
	size++;
	BTreeSize1(node->left);//分别遍历左右子树，每次遍历加一就可以计算出节点的个数
	BTreeSize1(node->right);
}
//方法二：递归调用,返回自身的节点个数和左子树的所有节点以及右子树的所有节点
int BTreeSize2(BTNode* node) {
	if (node == NULL) {
		return 0;//如果为空就返回0
	}
	return 1 + BTreeSize2(node->left) + BTreeSize2(node->right);

}

下面分析一下递归的方法（在初学二叉树的时候，画图真的是一个很友好的方式啦）

2，计算二叉树的高度

思路分析

递归思路，每个节点记录自己左右子树返回来的值，判断左右孩子哪边返回的值最大，最终用自身的加上大的那一边

代码实现

int BTreeHeight(BTreeNode* node) {
	if (node == NULL) {//如果为空，则返回0
		return 0;
	}
	int left = BTreeHeight(node->left);//计算左子树的高度
	int right = BTreeHeight(npde->right);//计算右子树的高度
	return left > right ? left + 1 : right + 1;//返回高度大的一遍，并且加上自身高度
}

3. 求二叉树中 第K层的节点个数

思路：

• 当k=1时，表示我们已经到达目标层级

• 当前非空节点就是我们要计数的节点，返回1

• 如果k>1，我们需要向下一层探索

• 分别计算左子树和右子树中第k-1层的节点数

• 将左右子树的结果相加返回

代码描述

int BTreeLevelKSize(BTNode* node,int k) {
	aseert(k > 0);//防止遇到不合法的k
	if (node == NULL) {
		return 0;
	}
	if (k == 1) {//第K层，节点数肯定为1
		return 1;
	}

	return BTreeLevelKSize(node->left, k - 1) + BTreeLevelKSize(node->right, k - 1);//加上左右子树的节点个数
}

4.查找节点中的值

思路：

• 如果节点为空，则不满足条件
• 分别在左右子树中查找
• 如果节点中的值与所要查找的值相等，就返回该节点的位置

代码描述

BTNode* BTreeFind(BTNode* root, BTDataType x) {
	if (root == NULL) {
		return NULL;
	}
	if (root->data == x) {
		return root;
	}
	BTNode* left = BTreeFind(root->left, x);
	BTNode* right = BTreeFind(root->right, x);
	if (left != NULL) {
		return left;
	}
	if (right != NULL) {
		return right;
	}
}

---

更多内容，敬请期待。