顺序查找
概念
暴力穷举,从头遍历,用if 将当前值与带查找值进行比较。
时间复杂度
查找成功的平均长度ASL
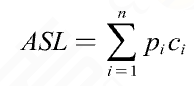
如果每个查找每个值的概率相等,pi = 1/n,那么 ASL = (n+1) / 2
所以时间复杂度为O(n)
代码实现
实例:
c
#include <stdio.h>
void search(char *arr, int length, int key) {
for(int i = 0; i < length; i++) {
if(arr[i] == key) {
printf("%d found at index %d\n", key, i);
return;
}
}
printf("%d not found\n", key);
}
int main(){
char arr[] = {8,12,5,16,55,24,20,18,36,6,50};
search(arr,sizeof(arr)/sizeof(arr[0]), 55);
return 0;
}折半查找(二分查找)
问题引入:给定一个长度为 n 的数组
nums,元素按从小到大的顺序排列且不重复,请查找并返回元素target在该数组中的索引。若数组不包含该元素,则返回 −1 。
概念
必须是已经排好序的有序数组,每次和中间的元素比较,如果比中间元素小,就在前半部分查找;否则在后半部分查找。
步骤:
-
初始化 i=0 和 j=n−1 ,分别指向数组首元素和尾元素,代表搜索区间 [0,n−1]
-
while( i <= j )
-
计算中点索引 m=⌊(i+j)/2⌋ ,其中 ⌊⌋ 表示向下取整操作。
-
判断
nums[m]和target的大小关系,分为以下三种情况。- 当
nums[m] < target时,说明target在区间 [m+1,j] 中,因此执行 i=m+1 。 - 当
nums[m] > target时,说明target在区间 [i,m−1] 中,因此执行 j=m−1 。 - else 当
nums[m] = target时,说明找到target,因此返回索引 m 。
- 当
-
-
若数组不包含目标元素,搜索区间最终会缩小为空。也就是循环结束还没有返回m,那么此时返回 −1 。
可视化过程 (具体可看《Hello算法》二分查找):
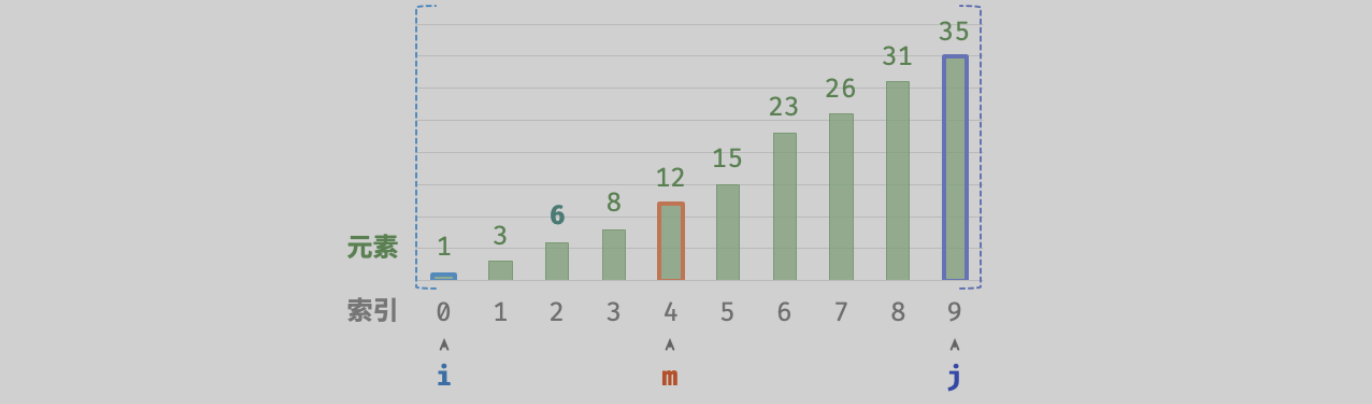
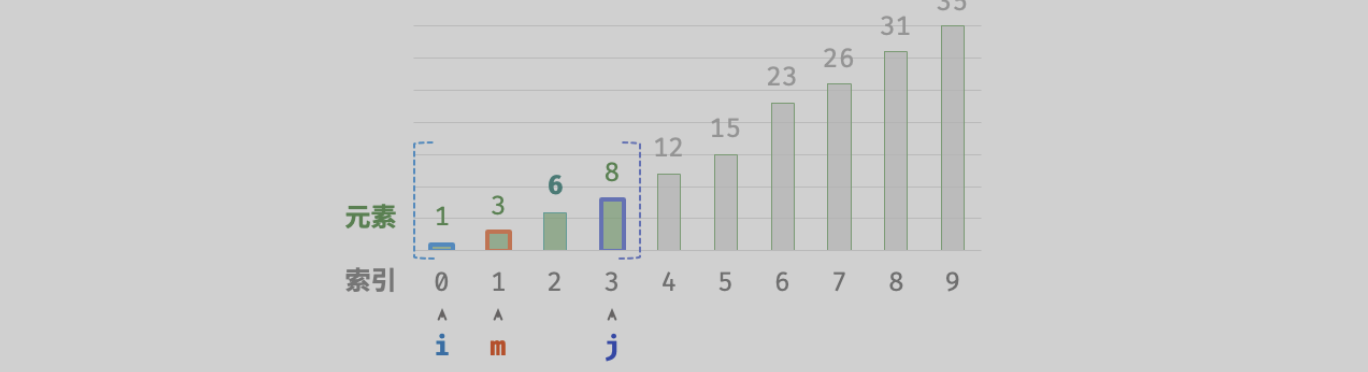
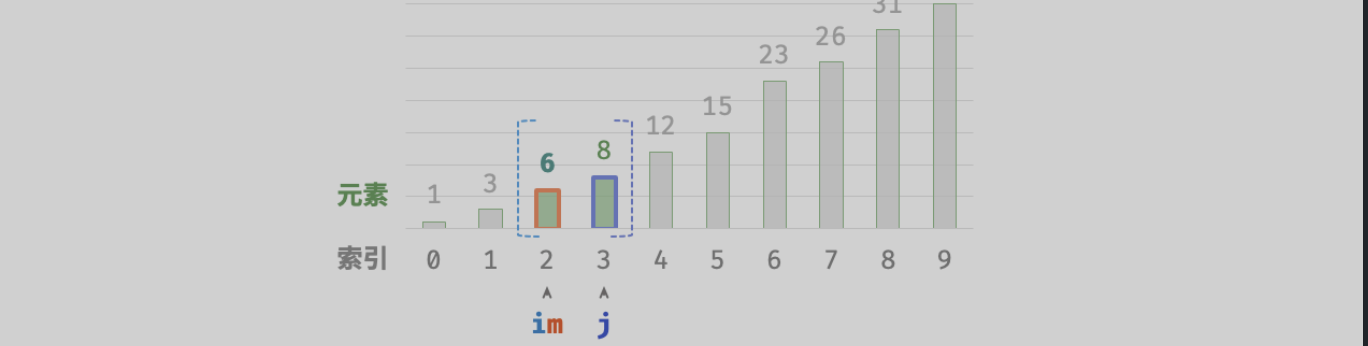
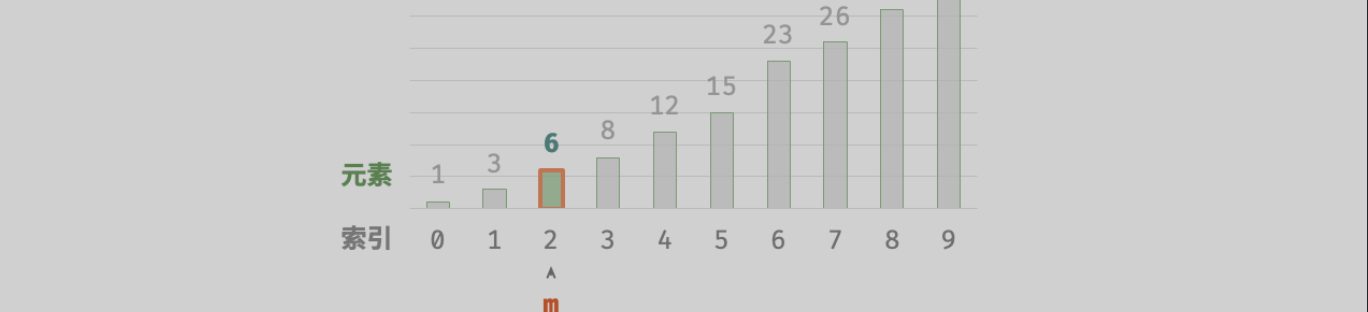
值得注意的是,由于 i 和 j 都是
int类型, 因此 i+j 可能会超出int类型的取值范围 。为了避免大数越界,我们通常采用公式 m=⌊i+(j−i)/2⌋ 来计算中点。
代码实现
实例:
非递归实现:
c
int binarySearch(int *arr, int length, int target) {
//初始化左右边界
int i = 0, j = length - 1, mid;
//区间[i,j]存在
while(i <= j){
mid = i + (j - i) / 2;
//目标在右半部分,也就是[mid+1,j]
if(arr[mid] < target){
i = mid+1;
}
//目标在左半部分,也就是[i,mid-1]
else if(arr[mid] > target){
j = mid-1;
}
//找到目标元素,arr[mid] == target
else{
return mid;
}
}
//没找到目标元素
return -1;
}递归实现:
c
int binarySearch_Recursive(int *arr, int target, int low, int high) {
//递归结束条件
if(low > high) return -1;
int mid = low + (high - low) / 2;
//目标在右半部分,也就是[mid+1,high]
if(arr[mid] < target){
return binarySearch_Recursive(arr, target, mid+1, high);
}
//目标在左半部分,也就是[low,mid-1]
else if(arr[mid] > target){
return binarySearch_Recursive(arr, target, low, mid-1);
}
//找到目标元素,arr[mid] == target
else{
return mid;
}
}二分查找的优缺点
下面直接照搬了《Hello算法》二分查找 的总结:
二分查找在时间和空间方面都有较好的性能。
- 二分查找的时间效率高。在大数据量下,对数阶的时间复杂度具有显著优势。例如,当数据大小 n=220 时,线性查找需要 220=1048576 轮循环,而二分查找仅需 log2220=20 轮循环。
- 二分查找无须额外空间。相较于需要借助额外空间的搜索算法(例如哈希查找),二分查找更加节省空间。
然而,二分查找并非适用于所有情况,主要有以下原因。
- 二分查找仅适用于有序数据。若输入数据无序,为了使用二分查找而专门进行排序,得不偿失。因为排序算法的时间复杂度通常为 O(nlogn) ,比线性查找和二分查找都更高。对于频繁插入元素的场景,为保持数组有序性,需要将元素插入到特定位置,时间复杂度为 O(n) ,也是非常昂贵的。
- 二分查找仅适用于数组。二分查找需要跳跃式(非连续地)访问元素,而在链表中执行跳跃式访问的效率较低,因此不适合应用在链表或基于链表实现的数据结构。
- 小数据量下,线性查找性能更佳。在线性查找中,每轮只需 1 次判断操作;而在二分查找中,需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法(减法),共 4 ~ 6 个单元操作;因此,当数据量 n 较小时,线性查找反而比二分查找更快。
二叉树查找
二叉排序树
左 < 根 < 右,除非左右子树是空
- 如果左子树非空,那么就要满足: 左子树上所有结点的值 < 根结点的值
- 如果右子树非空,那么就要满足: 右子树上所有结点的值 > 根结点的值
- 左右子树本身各自也是一颗二叉排序树
举例
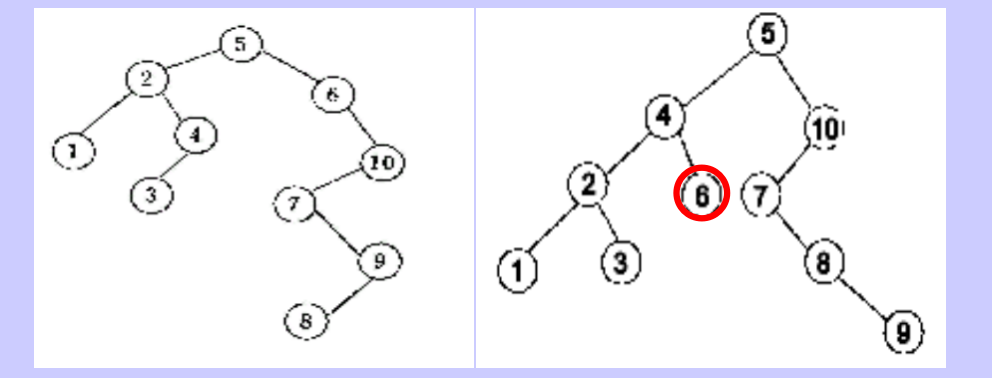
第二个图不是二叉排序树
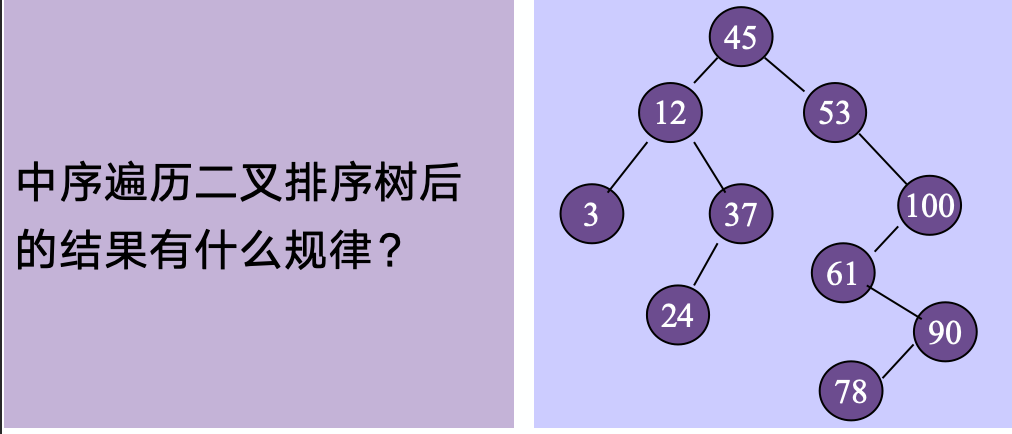
中序遍历:3 12 24 37 45 53 61 78 90 100
二叉排序树的特性:中序遍历二叉排序树,可以得到key的递增有序序列
二叉排序树的查找
左 < 根 < 右
- key == 根结点 ,返回
- 否则:
- key < 根结点,去这个结点的左子树找
- key > 根结点,去这个结点的右子树找
比较的是key和T->data.key (根结点的key)
代码实现
递归实现:
c
BSTree SearchBST(BSTree T,KeyType key)
{
if((!T) || key==T->data.key)
return T;
else if (key<T->data.key)
return SearchBST(T->lchild,key); //在左子树中继续查找
else
return SearchBST(T->rchild,key); //在右子树中继续查找
}非递归实现:
c
TreeNode *search(BinarySearchTree *bst, int num) {
TreeNode *cur = bst->root;
// 循环查找,越过叶节点后跳出
while (cur != NULL) {
if (cur->val < num) {
// 目标节点在 cur 的右子树中
cur = cur->right;
} else if (cur->val > num) {
// 目标节点在 cur 的左子树中
cur = cur->left;
} else {
// 找到目标节点,跳出循环
break;
}
}
// 返回目标节点
return cur;
}二叉排序树的插入
- 树中已有,不再插入
- 树中没有,查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应为该叶子结点的左孩子或右孩子
插入的元素一定在叶结点上
举例说明:插入20
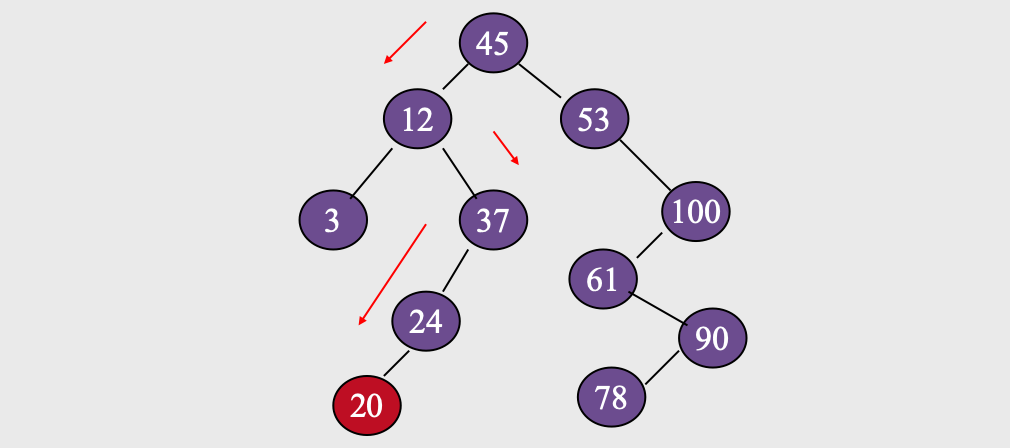
代码实现
递归实现:
c
void InsertBST(BSTree &T,ElemType e ) {
//当二叉排序树T中不存在关键字等于e.key的数据元素时,则插入该元素
if(!T) { //找到插入位置,递归结束
BSTree S = new BSTNode; //生成新结点*S
S->data = e; //新结点*S的数据域置为e
S->lchild = S->rchild = NULL; //新结点*S作为叶子结点
T =S; //把新结点*S链接到已找到的插入位置
}
else if (e.key< T->data.key)
InsertBST(T->lchild, e ); //将*S插入左子树
else if (e.key> T->data.key)
InsertBST(T->rchild, e); //将*S插入右子树
}非递归实现:
c
/* 插入节点 */
void insert(BinarySearchTree *bst, int num) {
// 若树为空,则初始化根节点
if (bst->root == NULL) {
bst->root = newTreeNode(num);
return;
}
TreeNode *cur = bst->root, *pre = NULL;
// 循环查找,越过叶节点后跳出
while (cur != NULL) {
// 找到重复节点,直接返回
if (cur->val == num) {
return;
}
pre = cur;
if (cur->val < num) {
// 插入位置在 cur 的右子树中
cur = cur->right;
} else {
// 插入位置在 cur 的左子树中
cur = cur->left;
}
}
// 插入节点
TreeNode *node = newTreeNode(num);
if (pre->val < num) {
pre->right = node;
} else {
pre->left = node;
}
}经过查找和插入,可以生成一颗二叉排序树
习题

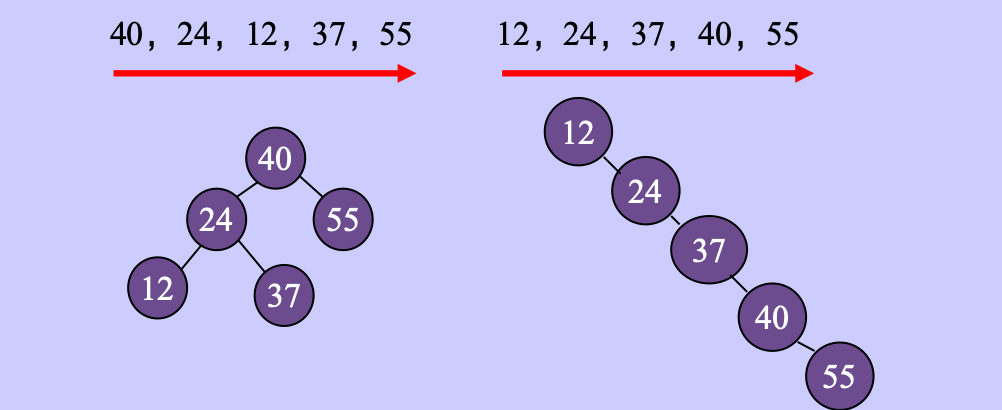
结果
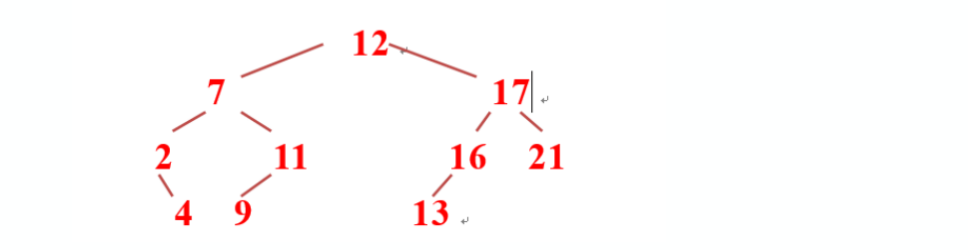
不同插入次序的序列生成不同形态的二叉排序树
二叉排序树的删除
-
删除叶结点,只需将其双亲结点指向它的指针清零,再释放它即可。

-
被删结点只有左子树,可以拿它的左子结点顶替它的位置,再释放它。
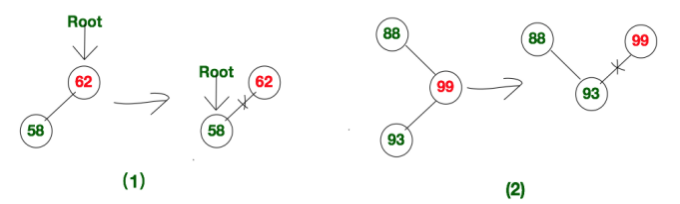
-
被删结点只有右子树,可以拿它的右子结点顶替它的位置,再释放它。
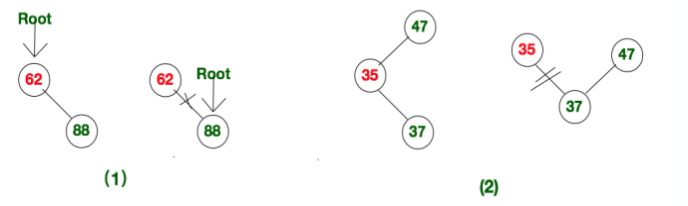
-
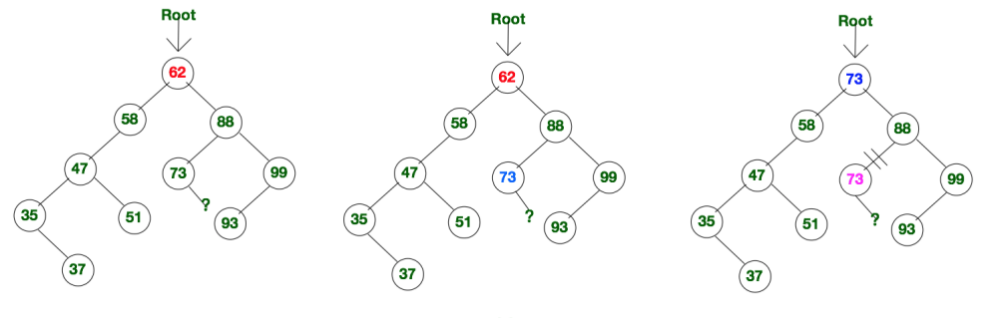
被删结点左、右子树都存在,可以在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删结点中,再来处理这个最小结点的删除问题。
二叉排序树的性能分析
第i层的结点,需要比较i次
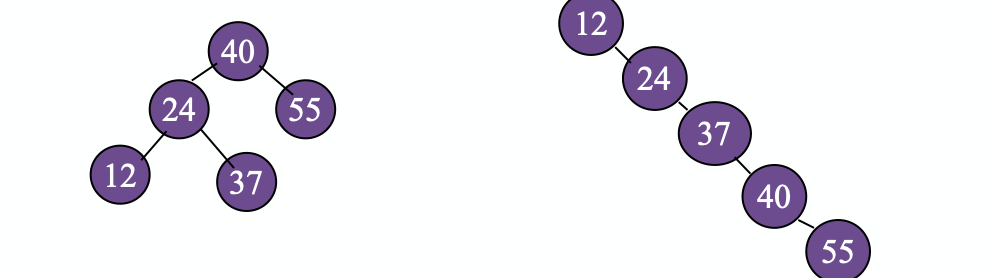
平均:
- ASL = (1 + 2 * 2 + 2 * 3) * (1/5) = 2.2
- ASL = (1 + 2 + 3 + 4 +5) / 5 = 3
最好:log2(n)
最坏:(n+1)/2
二叉排序树的优点
适合需要经常进行插入、删除和查找运算的表
平衡二叉树
怎么提高二叉排序树的查找效率呢?
尽量让二叉树的形状均衡 ------ 平衡二叉树
(所有结点的左、右子树深度之差的绝对值≤ 1)
平衡因子:该结点左子树与右子树的高度差
平衡二叉树的平衡因子只能是0、-1、1
性质:对于一棵有n个结点的AVL树,其高度保持在O(log2n)数量级,ASL也保持在O(log2n)量级。
哈希表查找
哈希表(hash table)又称散列表,它通过建立键 key 与值 value 之间的映射,实现高效的元素查询。具体而言,我们向哈希表中输入一个键 key ,则可以在 O(1) 时间内获取对应的值 value。

比如上面的图,只要键入一个key(学号)就能在O(1)内查找到value(姓名)。
哈希函数
将关键字 key 映射到存储地址的函数,记为hash(key) = Addr
设计哈希函数:
- 直接定址法:取key的某个线性函数作为哈希函数,hash(key) = a * key + b
- 除留余数法(最常用):取一个不大于表长的最大素数p,hash(key) = key % p
解决哈希冲突
哈希冲突:多个输入对应同一输出
建立哈希表的步骤:
- hash(key)
- 判断是否解决冲突
- 根据选择的冲突处理方法计算H',H'就是冲突key的存储地址
链式地址法
链式地址的基本概念:
- 相同哈希地址的key 链成一个单链表,m个哈希地址就设m个单链表
- 然后用一个数组存储每个单链表的头指针,形成一个动态的结构
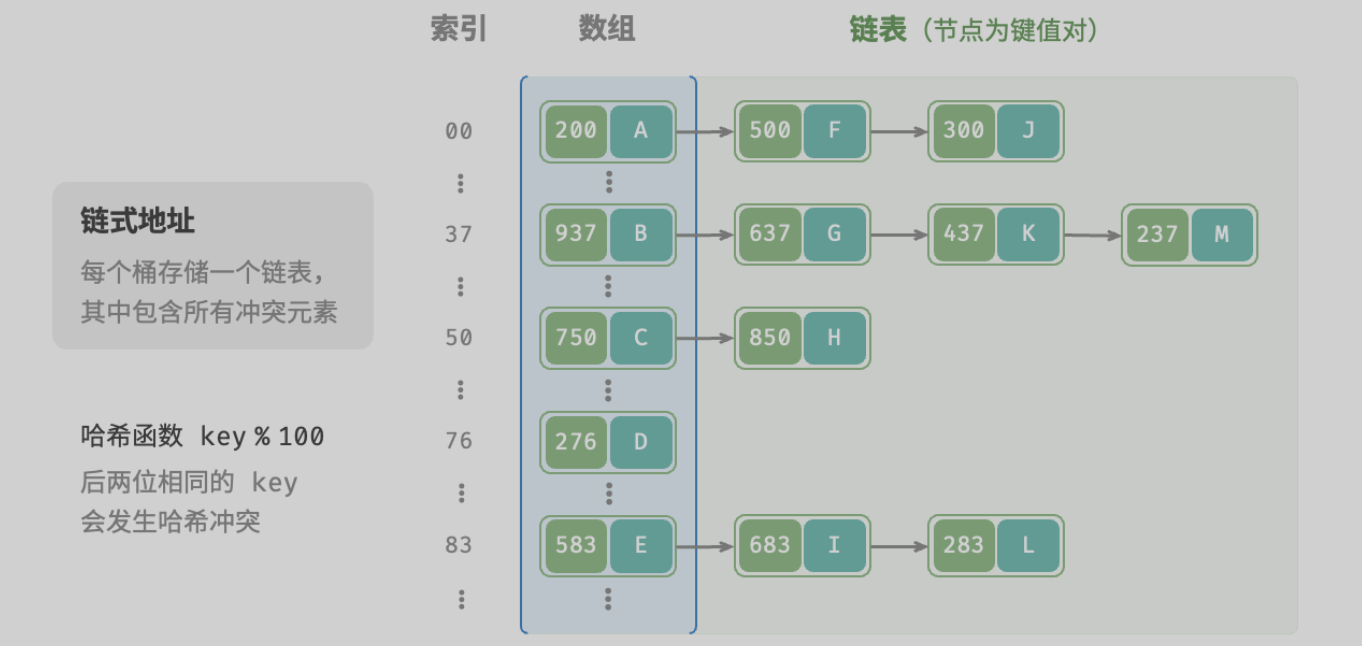
链式地址的优点:
- 非同义词不会冲突,无"聚集"现象
- 链表上结点空间动态申请,更适合于表长不确定的情况
开放寻址法
di 为增量序列,m是表长
1. 线性探测¶
Hi = ( hash(key) + di) % m
di = i ,(i = 1,2,...)
线性探测采用固定步长 的线性搜索来进行探测。若发现哈希冲突,则使用相同步长向后进行线性遍历,直到找到对应元素,返回 value 即可;如果遇到空桶,说明目标元素不在哈希表中,返回 None 。
删除一个key后要打上删除标记。
习题
第一题

解题步骤:

第二题

注意这里表长m = 15
Hi = (hash(key)+di) % 15
比较次数要加上第一次判断是否冲突的一次
解题步骤:

2. 二次探测(平方探测)¶
Hi=( Hash(key) ± di ) % m
di = i^2
平方探测与线性探测类似,都是开放寻址的常见策略之一。当发生冲突时,平方探测不是简单地跳过一个固定的步数,而是跳过"探测次数的平方"的步数,即 1,4,9,... 步。
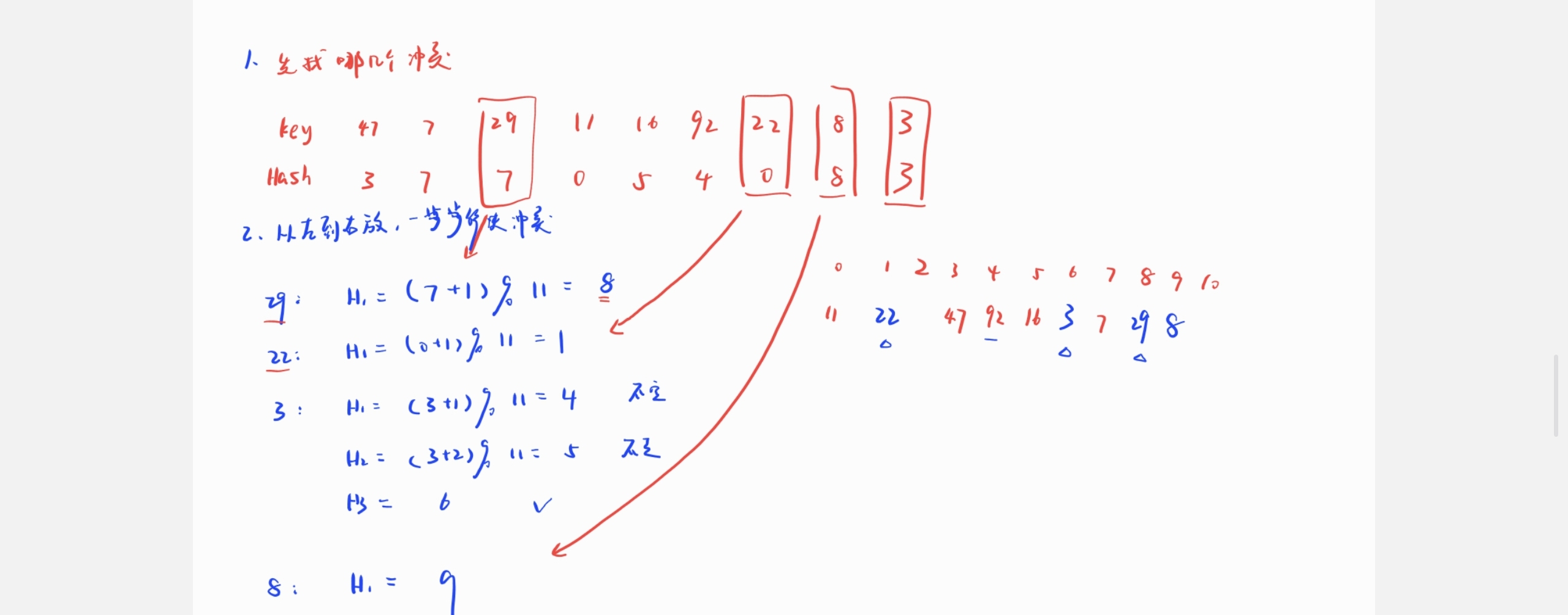
习题
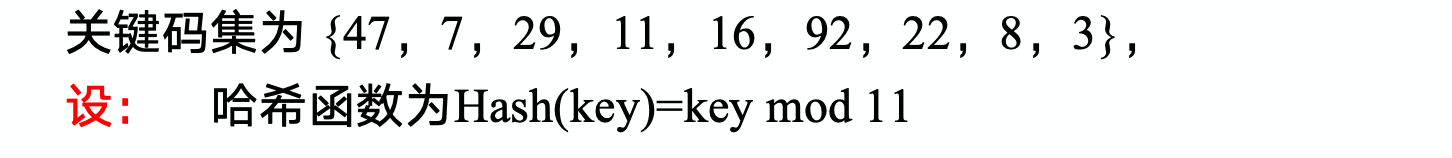
解题步骤:
3.伪随机探测
Hi = ( Hash(key) + di ) % m
di为随机数
和线性探测一样,删除一个key后也要打上删除标记
4. 多次哈希¶
多次哈希方法使用多个哈希函数 f1(x)、f2(x)、f3(x)、... 进行探测。
这个方法一般不用