【数据结构与算法】数据结构初阶：详解排序（二）——交换排序中的快速排序

艾莉丝努力练剑2025-07-28 22:17

🔥个人主页：艾莉丝努力练剑

❄专栏传送门：《C语言》、《数据结构与算法》、C语言刷题12天IO强训、LeetCode代码强化刷题

🍉学习方向：C/C++方向

⭐️人生格言：为天地立心，为生民立命，为往圣继绝学，为万世开太平

**重要提醒：**为什么我们要学那么多的数据结构？这是因为没有一种数据结构能够去应对所有场景。我们在不同的场景需要选择不同的数据结构，所以数据结构没有谁好谁坏之分，而评估数据结构的好坏要针对场景，如果在一种场景下我们需要频繁地对头部进行插入删除操作，那么这个时候我们用链表；但是如果对尾部进行插入删除操作比较频繁，那我们用顺序表比较好。

因此，不同的场景我们选择不同的数据结构。

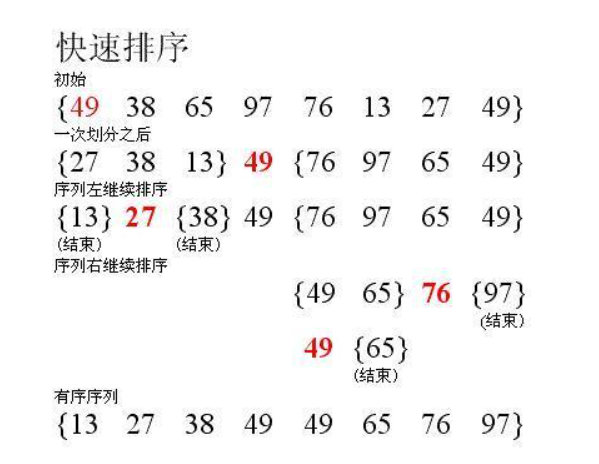
**前言：**本篇文章，我们继续来介绍排序相关的知识点，在初阶的数据结构与算法阶段，我们把知识点分成三部分，复杂度作为第一部分，顺序表和链表、栈和队列、二叉树为第二部分，排序为第二部分，我们之前已经介绍完了第一部分：算法复杂度和第二部分：顺序表和链表、栈和队列、二叉树。本文我们继续开始学习第三部分中的排序的内容啦。

这个用来测试代码的对比排序性能的代码博主还是放在下面，大家可以对比一下各种排序算法的运行时间，从而对不同排序方法的时间复杂度有更加直观地认识：

代码演示：

cpp 复制代码 
//测试排序的性能对比  
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	//begin和end的时间差就是
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

大家可以用一用，如果是直接选择排序、冒泡排序这种大家耐心一点，可能要多等一会儿，毕竟时间复杂度**O(n^2)**这一块，哈哈。

目录

正文

[一. 比较排序](#一. 比较排序)

三、交换排序

（二）快速排序

1、递归版本

（1）Hoare版本

1) 找基准值 找基准值)

2) 代码实现 代码实现)

3) 时间复杂度分析 时间复杂度分析)

​编辑

（2）挖坑法

1) 找基准值 找基准值)

2) 代码实现 代码实现)

（3）Lomuto双指针版本

1) 找基准值 找基准值)

2) 代码实现 代码实现)

（4）快速排序的时间复杂度分析

2、非递归版本------栈

1) 找基准值 找基准值)

2) 代码实现 代码实现)

3、快速排序的特性

结尾

正文

一. 比较排序

三、交换排序

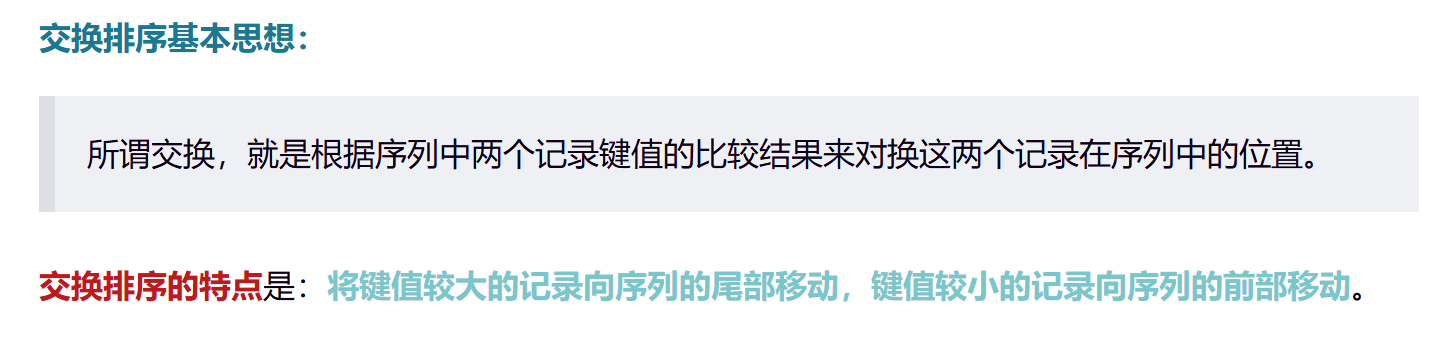
交换排序的概念在上一篇文章，博主直接截图，大家看一看：

（二）快速排序

重头戏来了，前面的几种排序算法大家可能没什么感觉，但从这个开始，那真是一个赛一个带派。

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

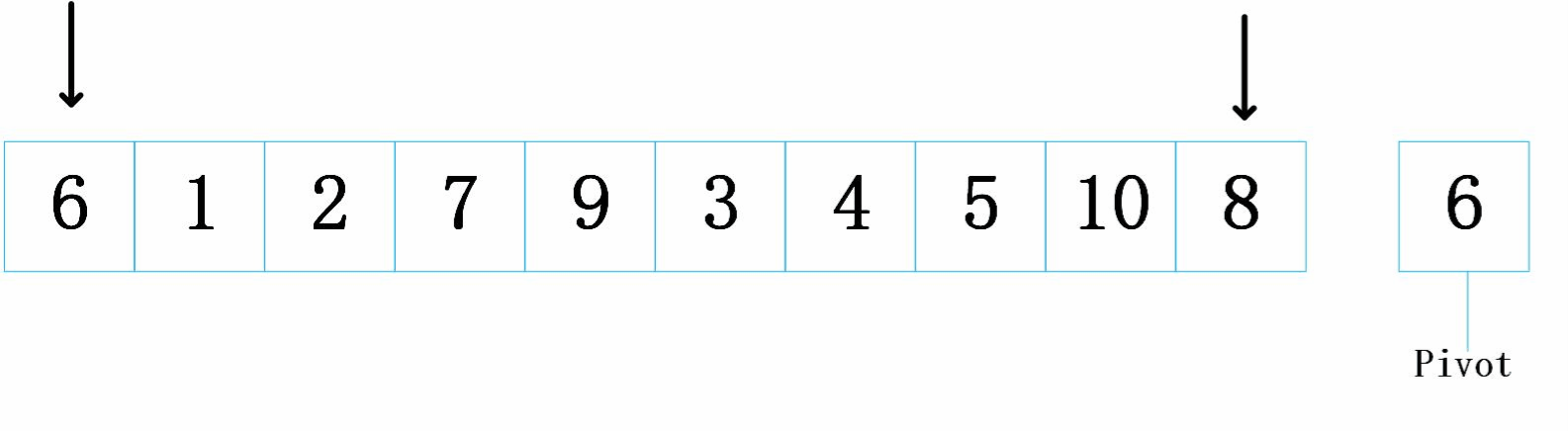
这个就是我们会介绍的快排找基准值的第一种方法------Hoare版本的思路。

首先，我们实现一下快速排序的主体框架的代码------

代码实现：

cpp 复制代码 
//快速排序
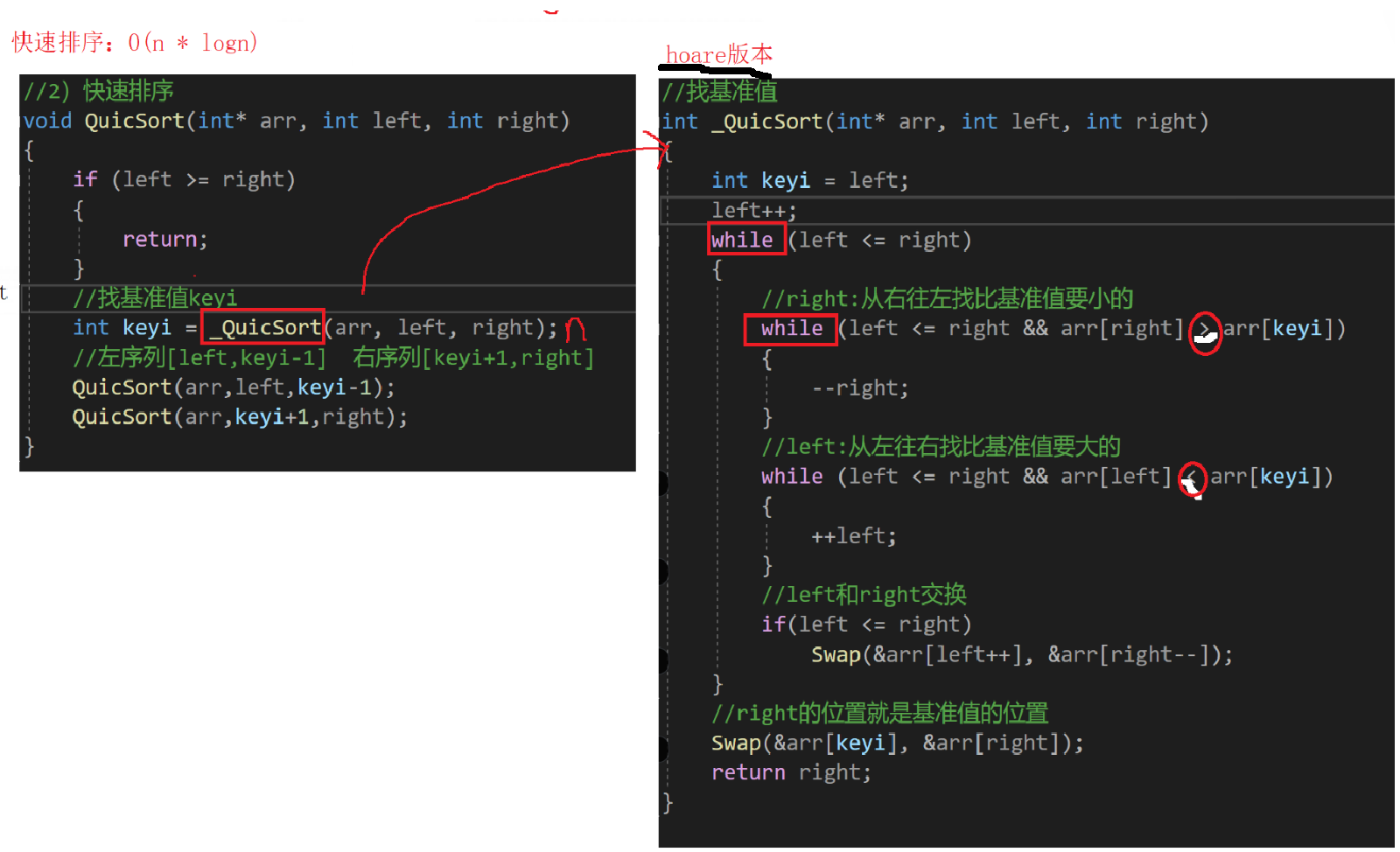
void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	//找基准值keyi
	int keyi = _QuickSort(arr, left, right);
	//左序列[left,keyi-1]  右序列[keyi+1,right]
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

我们根据是否递归，分为递归版本和非递归版本，递归版本又因为找基准值方法的不同，我们分成了Hoare版本、挖坑法以及Lomuto双指针法。

1、递归版本
（1）Hoare版本

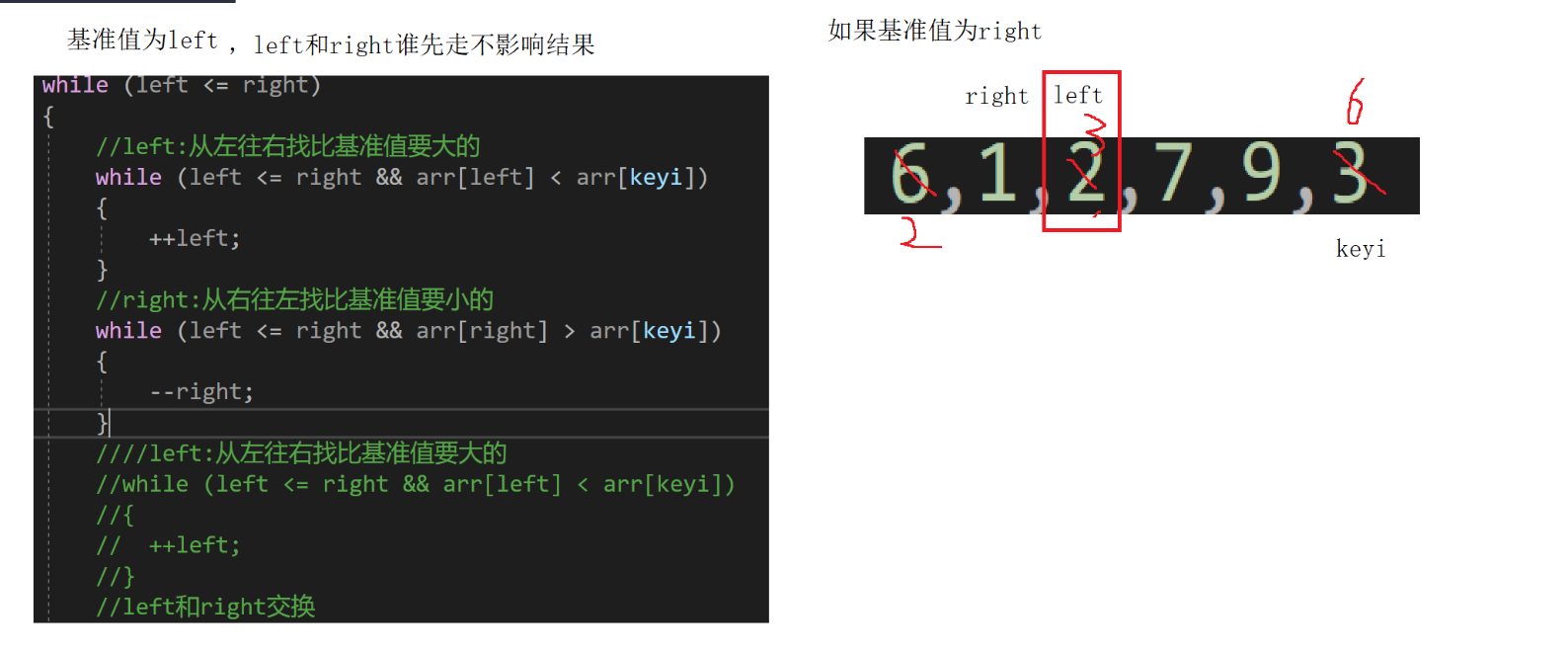
Hoare版本算法思路：

1）创建左右指针，确定基准值；

2）从右向左找出比基准值小的数据，从左向右找出比基准值大的数据，左右指针数据交换，进入下一次循环。

1) 找基准值

如果基准值找的不好，时间复杂度就会出问题，变成O(N^2)：

我们观察一下找基准值时候会遇到的一些问题------

为什么跳出循环后right位置的值⼀定不大于key？

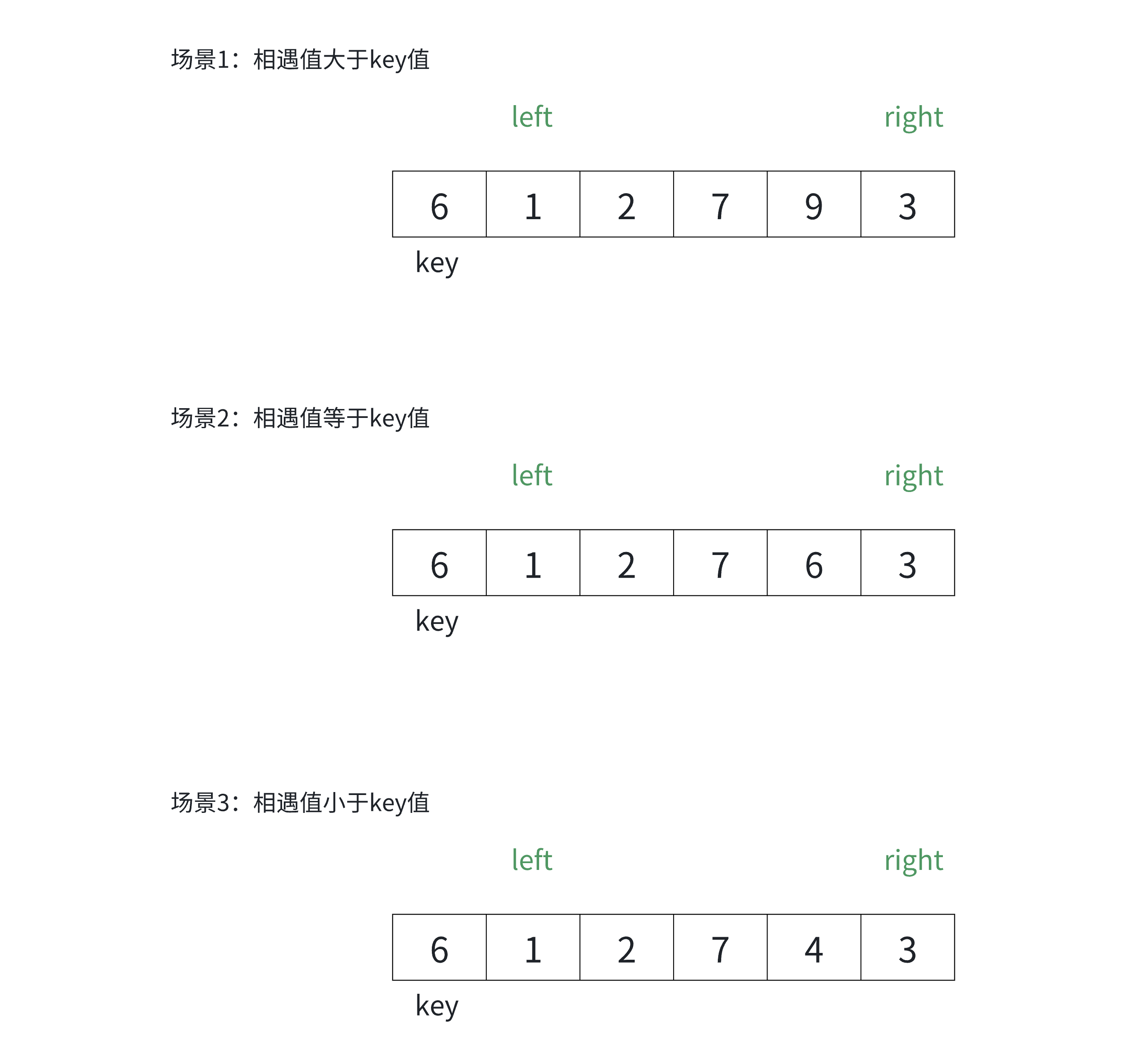
原因：

为什么left和right指定的数据和key值相等时也要交换？

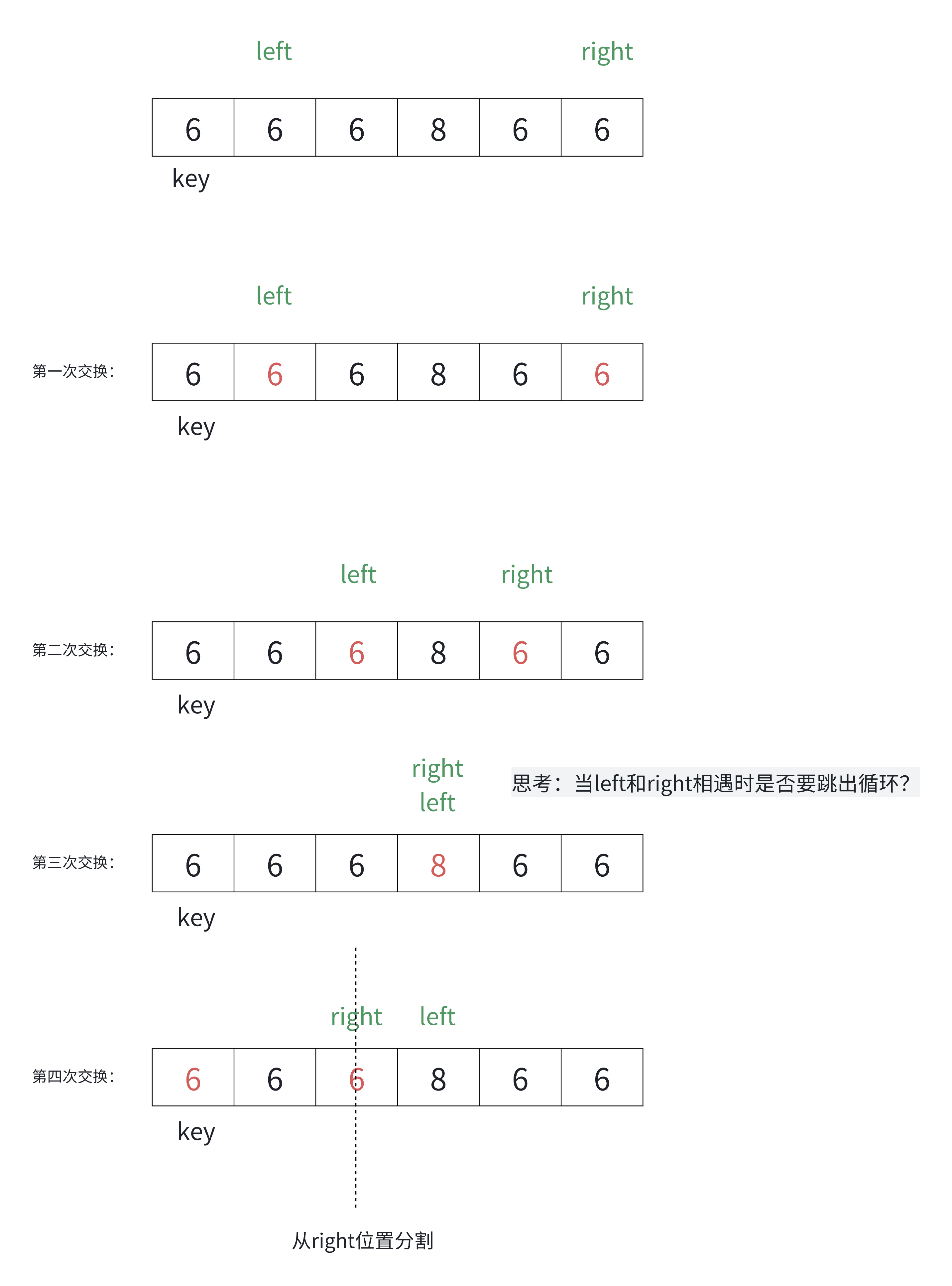
原因：

相等的值参与交换确实有一些额外消耗。实际还有各种复杂的场景，假设数组中的数据大量重复时，无法进行有效的分割排序。

**在这里，我们能不能让left先走，right后走呢？**不可以------

我们用一些用例测试的时候很多情况下能过，但我们不能这么做。

2) 代码实现
cpp 复制代码 
//找基准值  hoare版本
int _QuickSort1(int* arr, int left,int right)
{
	int keyi = left;
	left++;
	while (left <= right)
	{
		//right：从右往左找比基准值小的
		while (left <= right && arr[right] > arr[keyi])
		{
			--right;
		}
		//left：从右往左找比基准值大的
		while (left <= right && arr[left] < arr[keyi])
		{
			++left;
		}
		//left和right交换
		if (left <= right)
			Swap(&arr[left++], &arr[right--]);
	}
	//right的位置就是基准值的位置
	Swap(&arr[keyi], &arr[right]);
	return right;
}

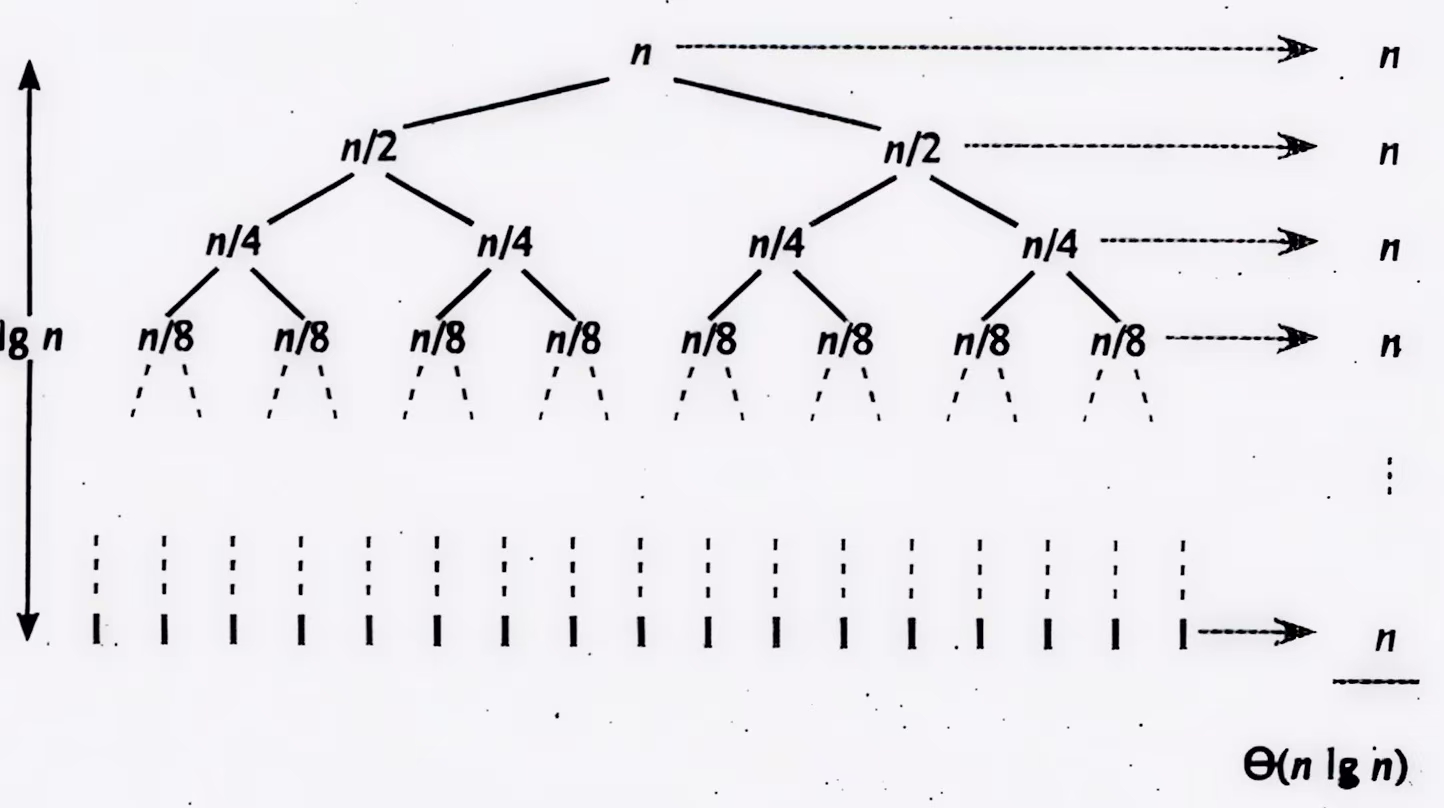
**时间复杂度：**O(n*logn)。

3) 时间复杂度分析

我们回忆一下，递归的时间复杂度是怎么求的：

如果基准值找的不好怎么办？

有友友可能会问：内层循环的while循环这里可不可以等于？不可以。

理由如下：

right位置一定会是基准值的位置吗？为什么？

（2）挖坑法

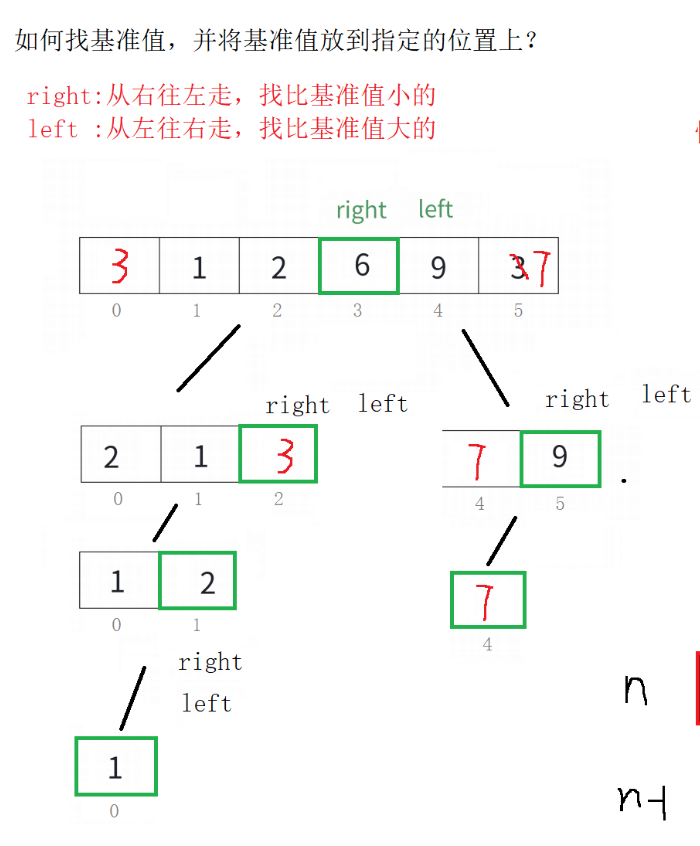
我们的思路：创建左右指针。⾸先从右向左找出比基准小的数据，找到后立即放入左边坑中，当前位置变为新的"坑"，然后从左向右找出比基准大的数据，找到后立即放入右边坑中，当前位置变为新的"坑"，结束循环后将最开始存储的分界值放入当前的"坑"中，返回当前"坑"下标（即分界值下标）。

1) 找基准值

我们的思路是：

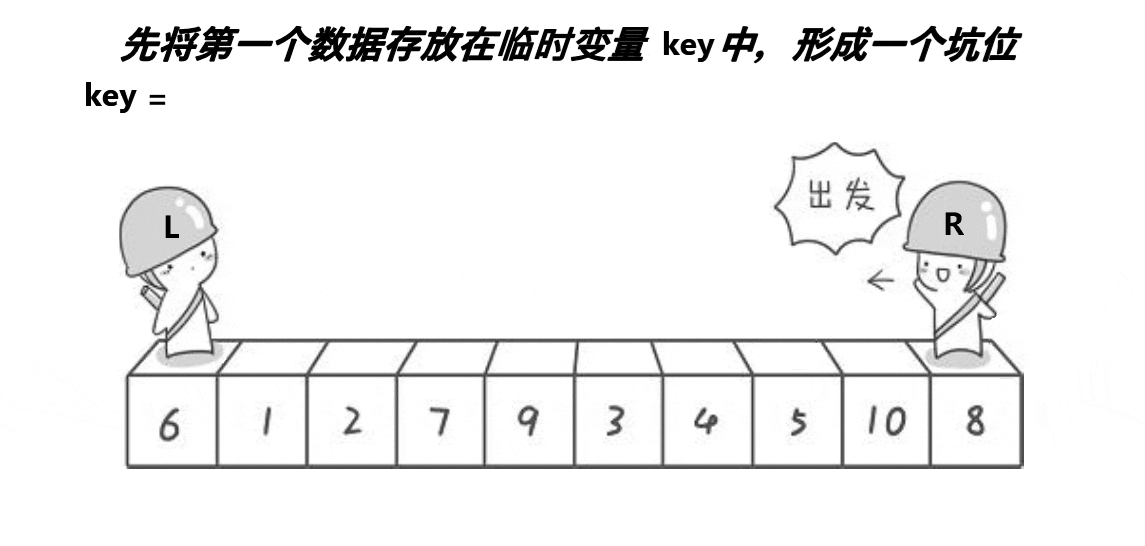
我们在上图的基础上进一步分析------

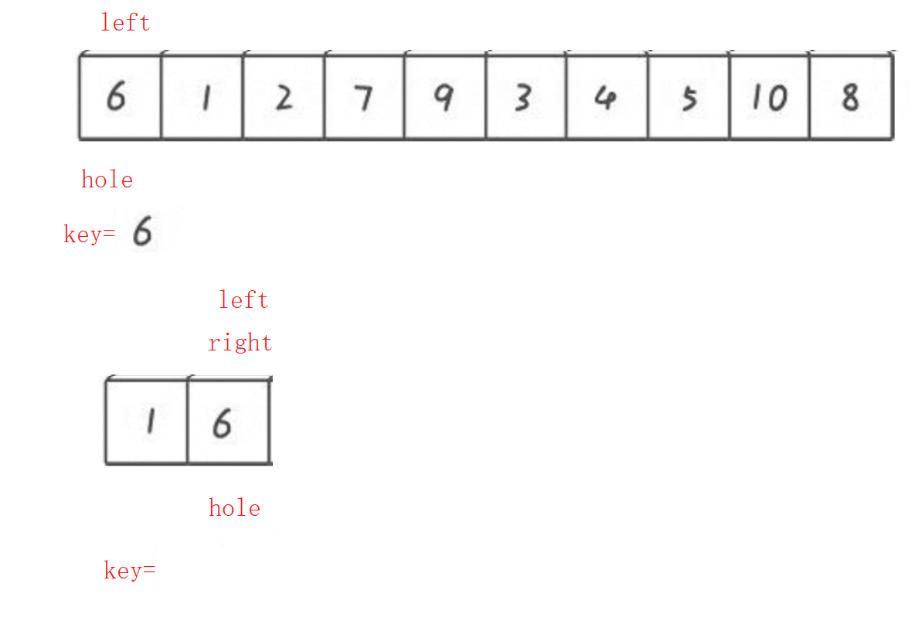
2) 代码实现
cpp 复制代码 
//找基准值  挖坑法
int _QuickSort2(int* arr, int left,int right)
{
	int hole = left;
	int key = arr[hole];
	while (left < right)
	{
		while (left < right && arr[right] > key)
		{
			right--;
		}
		arr[hole] = arr[right];
		hole = right;

		while (left < right && arr[left < key])
		{
			++left;
		}
		arr[hole] = arr[left];
		hole = left;
	}
	arr[hole] = key;
	return hole;
}

**时间复杂度：**O(n*logn)。

（3）Lomuto双指针版本

这是博主觉得最带派的找基准值的方法。

**思路：**创建前后指针，从左往右找比基准值小的进行交换，使得小的都排在基准值的左边。

1) 找基准值

根据上图，我们进一步分析，详见下图------

2) 代码实现
cpp 复制代码 
//找基准值 lomuto双指针方法
int _QuickSort(int* arr, int left,int right)
{
	int prev = left, cur = prev + 1;
	int keyi = left;
	while (cur <= right)
	{
		//cur数据和基准值比较
		if (arr[cur] < arr[keyi] && ++prev != cur)
		{
			Swap(&arr[cur], & arr[prev]);
		}
		++cur;
	}
	Swap(&arr[keyi], &arr[prev]);
	return prev;
}

**时间复杂度：**O(n*logn)。

（4）快速排序的时间复杂度分析

快速排序特性总结：

1、时间复杂度：O(nlogn)；

2、空间复杂度：O(logn)。

2、非递归版本------栈

要用非递归版本的快速排序，我们需要借助之前学过的数据结构------栈。

要用栈，我们之前已经介绍堆排序的时候就已经介绍过了类似的处理方法，这里不再赘述，

1) 找基准值
2) 代码实现

要用栈，栈这种数据结构我们在之前就已经实现过了，这里可以直接调用------

Stack.h：

cpp 复制代码 
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int STDataType;
typedef struct Stack
{
	STDataType* arr;
	int top;//定义栈中有效的数据个数
	int capacity;//栈的空间大小
}ST;

//初始化
void STInit(ST* ps);

//销毁
void STDestory(ST* ps);

//入栈------栈顶
void STPush(ST* ps, STDataType x);

//出栈------栈顶
void STPop(ST* ps);

//取栈顶元素
STDataType STTop(ST* ps);

//栈是否为空
bool STEmpty(ST* ps);

//获取栈中有效元素个数
int STSize(ST* ps);

Stack.c：

cpp 复制代码 
#define  _CRT_SECURE_NO_WARNINGS  1

#include"Stack.h"

//初始化
void STInit(ST* ps)
{
	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

//销毁
void STDestory(ST* ps)
{
	if (ps->arr)
		free(ps->arr);

	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

//入栈------栈顶
void STPush(ST* ps, STDataType x)
{
	assert(ps);
	//判断空间是否足够
	if (ps->top == ps->capacity)
	{
		//增容
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
	//空间足够
	ps->arr[ps->top++] = x;
}

//栈是否为空
bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

//出栈------栈顶
void STPop(ST* ps)
{
	assert(!STEmpty(ps));
	ps->top--;
}

//取栈顶元素
STDataType STTop(ST* ps)
{
	assert(!STEmpty(ps));
	return ps->arr[ps->top - 1];
}

//获取栈中有效元素个数
int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

sort.c：

cpp 复制代码 
//非递归版本快速排序------栈：栈+lomuto双指针
void QuickSortNorR(int* arr, int left,int right)
{
	ST st;
	STInit(&st);
	STPush(&st, right);
	STPush(&st, left);
	while (!STEmpty(&st))
	{
		//取栈顶两次
		int begin = STTop(&st);
		STPop(&st);
		int end = STTop(&st);
		STPop(&st);
		//[begin,end]------------找基准值
		int keyi = begin;
		int prev = begin, cur = prev + 1;
		while (cur <= end)
		{
			if (arr[cur] < arr[keyi] && ++prev != cur)
			{
				Swap(&arr[prev], &arr[cur]);
			}
			++cur;
		}
		Swap(&arr[prev], &arr[keyi]);
		keyi = prev;
		//begin  keyi  end
		//左序列[begin,keyi-1]
		//右序列[keyi+1,end]
		if (keyi + 1 < end)
		{
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, begin);
		}
	}
	STDestory(&st);
}

**时间复杂度：**O(n*logn)。

3、快速排序的特性

1、快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序；

2、时间复杂度：O(N*logN)------

3、空间复杂度：O(logN)；

4、稳定性：不稳定。

结尾

快速排序还有一些内容难度是加深的，如三路划分、自省排序，博主都整理到另一篇文章作为加餐了。后面归并排序出了递归、非递归版本，也会有加餐内容，敬请期待！

往期回顾：

【数据结构与算法】数据结构初阶：详解排序（一）------插入排序、选择排序以及交换排序中的冒泡排序

本期内容需要回顾的C语言知识如下面的截图中所示（指针博主写了6篇，列出来有水字数嫌疑了，就只放指针第六篇的网址，博主在指针（六）把指针部分的前五篇的网址都放在【往期回顾】了，点击【传送门】就可以看了）。

大家如果对前面部分的知识点印象不深，可以去上一篇文章的结尾部分看看，博主把需要回顾的知识点相关的博客的链接都放在上一篇文章了，上一篇文章的链接博主放在下面了：

【数据结构与算法】数据结构初阶：详解顺序表和链表（三）------单链表（上）

**结语：**本篇文章到这里就结束了，对数据结构的排序知识感兴趣的友友们可以在评论区留言，博主创作时可能存在笔误，或者知识点不严谨的地方，大家多担待，如果大家在阅读的时候发现了行文有什么错误欢迎在评论区斧正，再次感谢友友们的关注和支持！

相关推荐
草莓熊Lotso1 小时前
【数据结构初阶】--二叉树(二)
c语言·数据结构·经验分享·其他
Villiam_AY2 小时前
Redis 缓存机制详解：原理、问题与最佳实践
开发语言·redis·后端
UQWRJ3 小时前
菜鸟教程R语言一二章阅读笔记
开发语言·笔记·r语言
岁忧4 小时前
macOS配置 GO语言环境
开发语言·macos·golang
朝朝又沐沐5 小时前
算法竞赛阶段二-数据结构（36）数据结构双向链表模拟实现
开发语言·数据结构·c++·算法·链表
魔尔助理顾问5 小时前
系统整理Python的循环语句和常用方法
开发语言·后端·python
Ares-Wang6 小时前
JavaScript》》JS》 Var、Let、Const 大总结
开发语言·前端·javascript
薰衣草23336 小时前
一天两道力扣（6）
算法·leetcode
剪一朵云爱着6 小时前
力扣946. 验证栈序列
算法·栈
遇见尚硅谷6 小时前
C语言:*p++与p++有何区别
c语言·开发语言·笔记·学习·算法
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02扣子开源本地部署教程 丨Coze智能体小白喂饭级指南03Coze 开源了，送上保姆级私有化部署方案【建议收藏】04全球最强模型Grok4，国内已可免费使用！（附教程）05KGG转MP3工具|非KGM文件|解密音频06腾讯还是太全面了，限时免费！超全CodeBuddy IDE保姆级教程！（附案例）0701-开源版COZE-字节 Coze Studio 重磅开源！保姆级本地安装教程，手把手带你体验08vue数据变化但页面不变09干翻 Typora！MilkUp：完全免费的桌面端 Markdown 编辑器！10【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致