力扣热题100之搜索二维矩阵 II

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。

每列的元素从上到下升序排列。

代码

方法一：直接全体遍历

这个方法很直接，但是居然没有超时，很震惊

bash 复制代码

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        for row in matrix:
            for element in row:
                if element==target:
                    return True
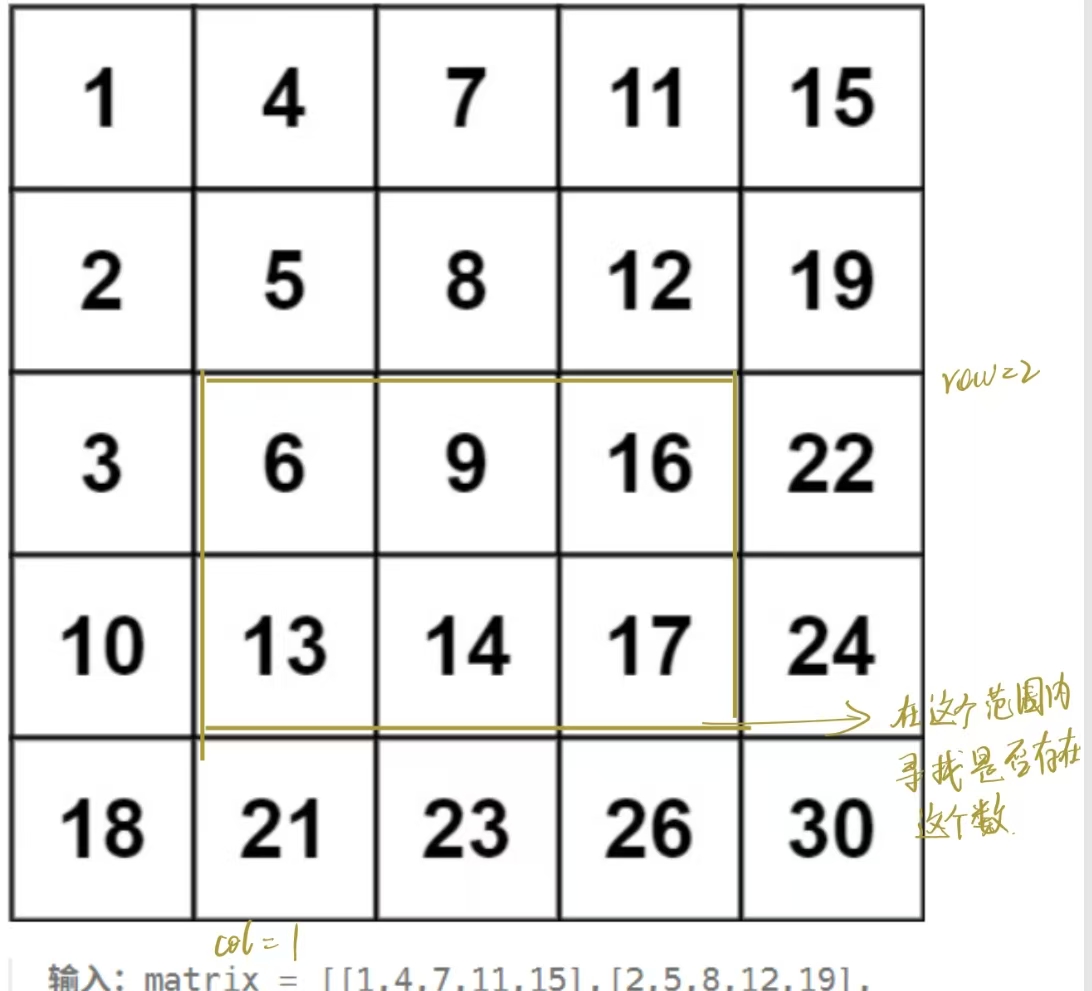
        return False

方法一：缩小搜索范围（自己想方法）

这个方法是通过边界缩小搜索的范围

bash 复制代码

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m=len(matrix)
        n=len(matrix[0])
        row=0
        col=0
        for i in range(m):
            if matrix[i][n-1]>target:
                row=i
                break
            elif matrix[i][n-1]==target:
                return True
        for j in range(n):
            if matrix[m-1][j]>target:
                col=j
                break
            elif matrix[m-1][j]==target:
                return True
        for i in range(row,m-1):
            for j in range(col,n-1):
                if matrix[i][j]==target:
                    return True
        return False

方法三：二分法

在矩阵的每一行中使用二分法查找target的应该插入的位置索引，代码中是使用的bisect中的bisect_left函数实现的

bisect_left是返回第一个大于等于目标值的位置（即插入后目标值位于所有相同值左侧）

bisect_left是返回第一个严格大于目标值的位置（即插入后目标值位于所有相同值右侧）

bash 复制代码

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        for row in matrix:
            idx=bisect.bisect_left(row, target)
            if idx<len(row) and row[idx]==target:
                return True
        return False

方法四：Z字形搜索

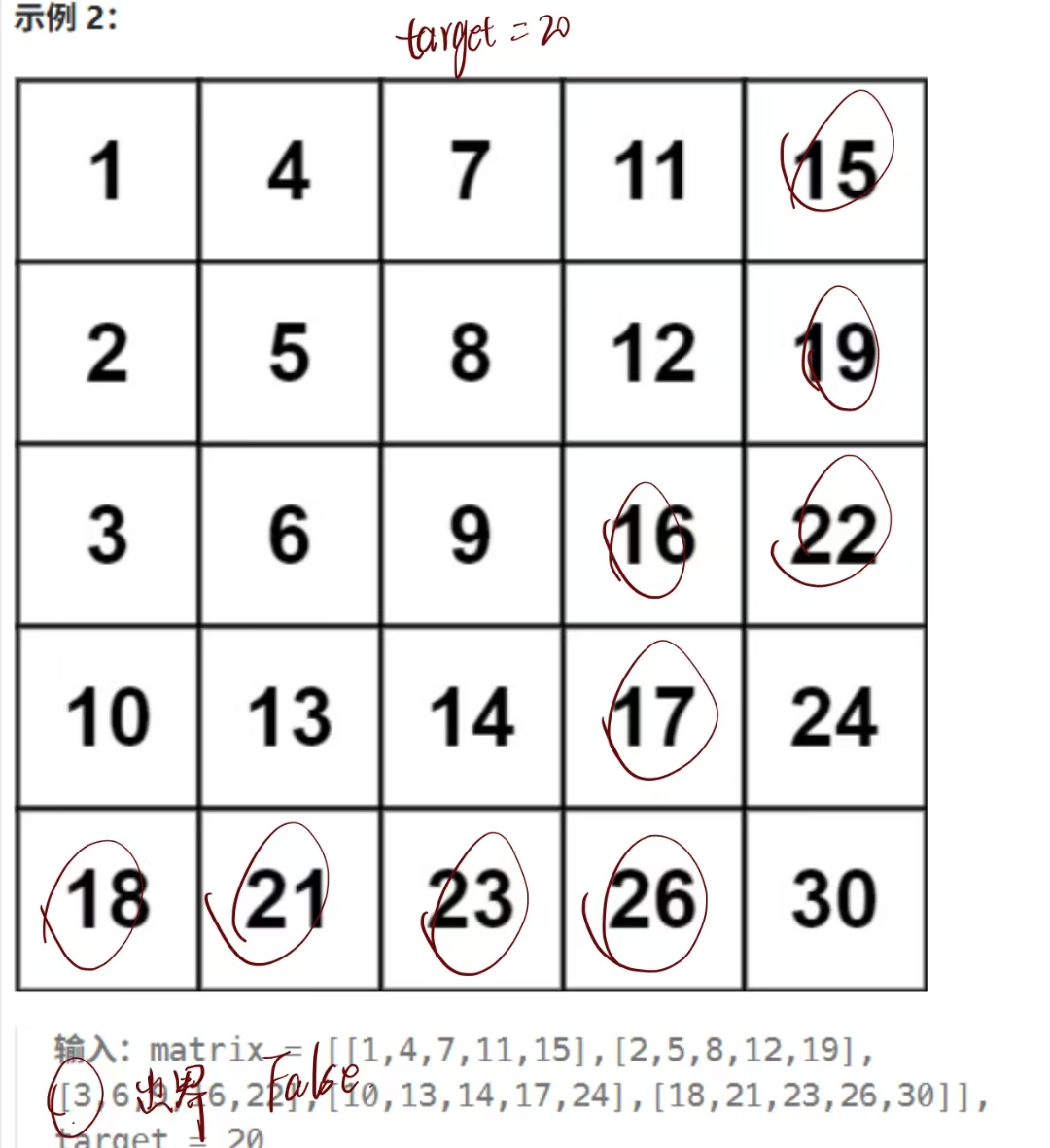
该方法就是从矩阵的右上角开始往矩阵的右下角搜索，如果当前值大于target，列标减一；如果当前值小于target，行标加一。很巧妙很有意思的一种方法

bash 复制代码

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m,n=len(matrix),len(matrix[0])
        x,y=0,n-1
        while x<m and y>=0:
            if matrix[x][y]==target:
                return True
            if matrix[x][y]>target:
                y-=1
            else:
                x+=1
        return False