数据结构*二叉树

树

树是一种非线性数据结构。

这就是抽象的树的结构。

对于一棵树来说，有N个结点，就有N-1条边

其中有许多概念：

根结点：对于上图来说就是A

子树：就是结点下面分开的部分。例如：A的子树就是以B为根结点的树和以C为根结点的树。

结点的度：就是这个节点含有子树的个数称为该节点的度。

树的度：就是这棵树所有节点的度的最大值。上图的树的度为3

叶子结点或终端结点：度为0的结点。例如：D、E、I、G、H

层次：根节点为第一层。

树的高度或深度：树的最大层次。例如：上图就是4

当然还有许多概念，可以自行查找

树的表示方法

对于树的表示方法有很多种，如：双亲表示法，孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。下面是孩子兄弟表示法。

二叉树

什么是二叉树

二叉树就是特殊的一种树，其每个结点最多有两棵子树 ，即结点的度最大为 2 。对于二叉树来说，左子树和右子树有严格顺序之分 ，次序不能颠倒 。如下图所示：

当然还有一些特殊的二叉树：满二叉树、完全二叉树。

满二叉树通俗来讲就是每一层的结点都是满的二叉树，如下图所示：

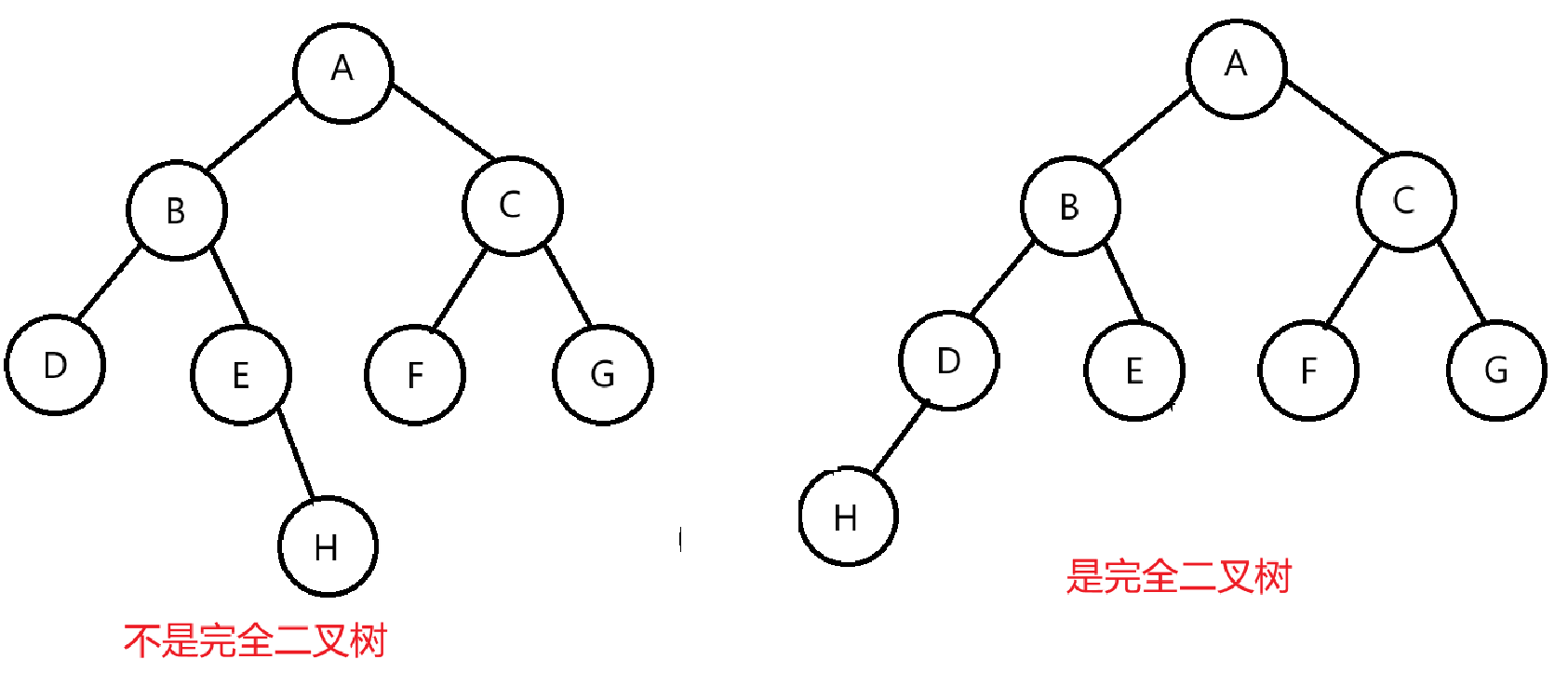
完全二叉树通俗来讲就是只有最后一层不是满的，其余层都是满的。但是最后一层的节点都是从最左边开始排 ，不会在中间空着 。如下图所示：

二叉树的一些性质

1、 一颗非空二叉树的第i层上最多有2^(i-1)个结点。
2、 一颗深度为k的二叉树，其树的最大结点为2^k-1
3、 由第二条性质推出，具有n个结点的完全二叉树的深度k = log(n+1) [以2为底的log] 向上取整。
4、 对于任意一颗二叉树，其叶子结点为n0(结点度为0)，度为2的结点个数为n2，则n0 = n2 + 1 。
5、 对于具有n个结点的完全二叉树，按照从上到下、从左到右的顺序从0开始编号，则对于序号i的结点：

左孩子结点下标为2i + 1，当2 i + 1 > n 时，就不存在左孩子结点。

右孩子结点下标为2i + 2，当2 i + 2 > n 时，就不存在右孩子结点。

其父亲结点的下标为(i - 1) / 2。i == 0时，其结点为根节点，没有父亲结点。

二叉树的存储

二叉树的存储方式主要有两种，分别是顺序存储和链式存储。顺序存储是把二叉树的节点按照层次依次存于数组中。链式存储是通过节点类来构建二叉树。

下面是用孩子表示法来构建二叉树

static class TreeNode{
    public char val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(char val) {
        this.val = val;
    }
}

二叉树的遍历

对于二叉树的遍历有四种：前序遍历、中序遍历、后序遍历、层序遍历。

下面遍历一这棵二叉树为例：

层序遍历

1、层序遍历就是从上到下从左到右开始访问结点。

输出为：A B C D E F G H
下面我们重点来说明前中后序遍历！ 对于这三种遍历的过程就好像递归一样，始终重复完成某一操作。

前序遍历

2、前序遍历就是按照先访问根，再访问左子树，最后访问右子树。在访问根的时候输出。

对应的流程如上图所示：按照根 -> 左子树 -> 右子树的访问顺序

输出为：A B D E H C F G

代码展示：

public void preOrder(TreeNode root) {
    if(root == null) {
        return;
    }
    System.out.print(root.val + " ");
    preOrder(root.left);
    preOrder(root.right);
}

代码解释：

代码采用递归的方式，将问题化成子问题，就是访问根，打印根，访问左树(root.left)，访问右树(root.right)。结束条件就是当root为空时，直接返回，说明已经访问到底了（这颗树已经访问完了）。

中序遍历

3、中序遍历就是按照先访问左子树，再访问根，最后访问右子树。在访问根的时候输出。

对应的流程如上图所示：按照左子树 -> 根 -> 右子树的访问顺序

输出为：D B E H A F C G

代码展示：

public void inOrder(TreeNode root){
    if(root == null) {
        return;
    }
    inOrder(root.left);
    System.out.print(root.val + " ");
    inOrder(root.right);
}

代码解释：

代码采用递归的方式，将问题化成子问题，就是访问左树(root.left)，访问根，打印根，访问右树(root.right)。结束条件就是当root为空时，直接返回，说明已经访问到底了（这颗树已经访问完了）。

后序遍历

4、后序遍历就是按照先访问左子树，再访问右子树，最后访问根。在访问根的时候输出。

对应的流程如上图所示：按照左子树 -> 右子树 -> 根的访问顺序

输出为：D H E B F G C A

代码展示：

public void postOrder(TreeNode root){
    if(root == null) {
        return;
    }
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.val + " ");
}

代码解释：

代码采用递归的方式，将问题化成子问题，就是访问左树(root.left)，访问右树(root.right)，访问根，打印根。结束条件就是当root为空时，直接返回，说明已经访问到底了（这颗树已经访问完了）。

二叉树的一些简单操作

求结点个数

代码展示：

// 获取树中节点的个数
private static int size= 0;
public int size1(TreeNode root) {//用计数的方式 -> 遍历
    if(root == null) {
        return 0;
    }
    size++;
    size1(root.left);
    size1(root.right);
    return size;
}
public int size(TreeNode root) {//子问题 -> 树的结点 = 左子树的结点 + 右子树的结点 + 1（root）
    if(root == null) {
        return 0;
    }
    return size(root.left) + size(root.right) + 1;
}

代码解释：

有两种思路：

1、用遍历思路，访问一个结点就size++

2、子问题思路：利用递归，将问题变成了"树的结点 = 左子树的结点 + 右子树的结点 + 1"

求叶子结点个数

代码展示：

// 获取叶⼦节点的个数
private static int count = 0;
public int getLeafNodeCount1(TreeNode root){//遍历思路 -> 左右子树都为null
    if(root == null) {
        return 0;
    }
    if(root.left == null && root.right == null) {
        count++;
    }
    getLeafNodeCount1(root.left);
    getLeafNodeCount1(root.right);
    return count;
}
public int getLeafNodeCount(TreeNode root){//子问题 -> 树的叶子结点 = 左子树的叶子节点 + 右子树的叶子节点
    if(root == null) {
        return 0;
    }
    if(root.left == null && root.right == null) {
        return 1;
    }
    return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}

代码解释：

有两种思路：

1、用遍历思路，访问一个结点当满足条件是就count++。当root == null时，也就说明了这棵树为空，没有结点。

2、子问题思路：利用递归，将问题变成了"树的叶子结点 = 左子树的叶子节点 + 右子树的叶子节点"，当满足条件时就说明是一个叶子结点。

求第K层节点的个数

代码展示：

public int getKLevelNodeCount(TreeNode root,int k){
	//当root为null时，说明这棵树提前走完了，还没有到第k层，也就没有第k层的结点
    if(root == null) {
        return 0;
    }
    //递归结束条件，当k==1时，说明已经走到了第k层
    if(k == 1) {
        return 1;
    }
    return getKLevelNodeCount(root.left,k - 1) + getKLevelNodeCount(root.right,k - 1);
}

代码解释：

将问题转换为左子树第k层的个数+右子树第k层的个数。此时层数逐次递减（k-1）。遍历到第k层就结束遍历了。

求二叉树的高度

代码展示：

public int getHeight(TreeNode root){//子问题 -> 左子树与右子树深度的最大值 + 1（root）
    if(root == null) {
        return 0;
    }
    return Math.max(getHeight(root.left),getHeight(root.right)) + 1;
}

代码解释：

将问题转换为"左子树与右子树深度的最大值 + 1（根结点本身高度1）"

检测值为val的元素是否存在

代码展示：

public TreeNode find(TreeNode root, int val){
    //当root为null时，也就没有val，返回null
    if(root == null) {
        return null;
    }
    //当匹配成功，就返回当前结点
    if(root.val == val) {
        return root;
    }
    //到这里说明没有匹配成功，访问左子树有没有
    TreeNode ret = find(root.left,val);//如果没有匹配成功，则ret为null
    //ret不为null，则返回找到的结点
    if(ret != null) {
        return ret;
    }
    //到这里说明左子树也都没有匹配成功
    ret = find(root.right,val);//开始在右子树找
    return ret;//找到了ret就是匹配的结点，没有就是null
}

代码解释：

也是利用递归，将问题换成"左子树找，再在右子树找"。

层序遍历

代码展示：

1、使用队列

public void levelOrder(TreeNode root){
    //当root为null时，就没有结点，直接返回
    if(root == null) {
        return;
    }
    Queue<TreeNode> queue = new LinkedList<>();//创建队列，将结点存储到队列中
    //从父亲结点开始，放入队列中
    queue.offer(root);
    while (!queue.isEmpty()) {//当将二叉树中的元素全部pop，此时queue为空，层序遍历完了
        TreeNode cur = queue.poll();//将队列中最上面的元素取出
        System.out.print(cur.val+" ");//打印
        //将其输出的左边的结点存入队列中（不为空）
        if(cur.left != null){
            queue.offer(cur.left);
        }
        //将其输出的右边的结点存入队列中（不为空）
        if(cur.right != null){
            queue.offer(cur.right);
        }
        //最后再通过循环将所有的结点的左右依次存入队列中，输出。
        //A -> B C(A的左右) -> D E(B的左右) F G(C的左右) -> H(E的右)
    }
}

2、使用嵌套列表+队列

public List<List<Character>> levelOrderPlus(TreeNode root) {
    List<List<Character>> ret = new ArrayList<>();
    if(root == null) {
        return ret;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {//当将二叉树中的元素全部pop，此时queue为空，层序遍历完了
        List<Character> curRow = new ArrayList<>();//每层创建一个新的列表

        //用来判断每层的个数。从父亲结点A一个 -> 经过while(size != 0)循环，列表中存入B D两个元素，列表中个数也就是2 -> 同理依次类推
        int size = queue.size();//进行分行处理，

        while (size != 0){
            TreeNode cur = queue.poll();//将队列中最上面的元素取出
            curRow.add(cur.val);//将这一层的元素存入当前列表中
            //将其输出的左边的结点存入队列中（不为空）
            if(cur.left != null){
                queue.offer(cur.left);
            }
            //将其输出的右边的结点存入队列中（不为空）
            if(cur.right != null){
                queue.offer(cur.right);
            }
            size--;
        }
        ret.add(curRow);//将这一层的列表存入列表中
    }
    return ret;//返回这个二维列表
}

代码解释：

方法一是使用队列，利用队列先进先出的特点，先将父亲结点放进去，然后就开始向队列存放元素。（具体过程：首先从队列出元素并打印，存放出来元素的左结点和右结点）如下图所示：

方法二是多使用了嵌套列表，是为了更好的区分每层的元素。利用每次队列中的size，来创建列表，再存入列表中。如下图所示：

判断是否为完全二叉树

完全二叉树和层序遍历有关，思路和层序遍历差不多，但使用队列时候，是需要存入null值的，这样好判断在中间是不是空着的。

代码展示：

public boolean isCompleteTree(TreeNode root){
    if(root == null) {
        return true;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode cur = queue.poll();
        if(cur == null){
            break;
        }else {
            queue.offer(cur.left);
            queue.offer(cur.right);
        }
    }
    while (!queue.isEmpty()) {
        if(queue.poll() != null) {
            return false;
        }
    }
    return true;
}

代码解释：

这里不需要判断cur的左右是否为空，直接进队列即可。当出队列的为null，说明层序遍历到了null。如果这是一棵完全二叉树，则剩下的结点都为null，也就是队列中的元素全为null；当不是一棵完全二叉树，队列中的元素中必然有结点。后面的while循环就是用来判断队列中是否全为null。