文化水平：初二
文章只介绍反比例函数的基础知识及其透彻的理解。文章需要掌握的前置知识：
- 初二上学期及以前学龄段的所有知识。
- 对函数和一次函数有透彻的理解。
- 对反比例函数知道且有一定的了解（不需要太多）。
文章需要用到的基本命题：
- 对于平面内的三个点\(A\)、\(B\)、\(C\)，如果满足\(AB+BC=AC\)或\(AB-BC=AC\)或\(BC-AB=AC\)，那么这三个点共线。反之也成立。
- 平面直角坐标系中存在的两个点\(A(x_a, y_a)\)、\(B(x_b, y_b)\)，有\(AB=\sqrt {(x_a-x_b)^2+(y_a-y_b)^2}\)。
- 对于平面内的三个点\(A\)、\(B\)、\(C\)，如果满足\(\angle {ABC}或\angle {BAC}或\angle {ACB}=180\degree\)，那么这三个点共线。反之也成立。
- 在平面直角坐标系中若存在两点\(A\)、\(B\)，则有：\(k_{AB}=\frac {y_A-y_B} {x_A-x_B}\)。式中，\(k_{AB}\)是一条过\(A\)、\(B\)两点的直线的斜率（或其一次函数解析式的\(k\)值）。
- 一个点\(P(x, y)\)关于原点对称的点\(P'\)坐标为\((-x, -y)\)。大家可以感性证明一下。提供定理：成中心对称的图形对应点与对称中心共线且对应点到对称中心的距离相等（对称中心为对应点连线的中点）。
- 成轴对称的两个图形对应点的连线被对称轴垂直平分。
- 线段垂直平分线上的点到线段两端的距离相等。
- 一个点\(P(x,y)\)关于直线\(y=x\)的对称点\(P'\)坐标设为\((y,x)\)。大家可以感性证明一下。由于比命题⑤难，这里提供一种证明：如图，点\(P\)和点\(P'\)关于直线\(y=x\)对称，立得\(y=x\)垂直平分\(PP'\)（⑥）。又得\(OP=OP'\)（⑦）。此时易证\(\triangle OPH≌\triangle OP'H'\)。由图可知\(PH=x, OH=y\)，由全等可得\(PH=P'H'=x, OH=OH'=y\)，则\(P'(y,x)\)。此证明可以类比延拓到第二、三、四象限的任意点\(P\)。命题得证。
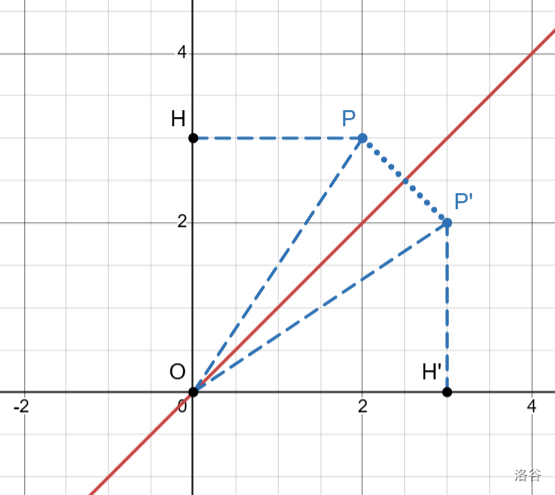
- 一个点\(P(x,y)\)关于直线\(y=-x\)的对称点\(P'\)坐标设为\((-y,-x)\)。可类比命题⑧证明。
- 对于一个正实数\(a\)，\(\sqrt a\)随\(a\)的增大而增大。（证明：函数\(y=\sqrt x\)值随\(x\)的增大而增大。）
来源和定义
课本上是这么给出反比例函数的来源的：
在小学里，我们已经知道，如果两个量的乘积一定，那么这两个量成反比例。
成反比例两个量之间的关系，怎样用函数表达式来描述呢？
定义：
一般地，形如\(y=\frac k x（k为常数，k\neq 0）\)的函数叫做反比例函数（inverse proportional function） ，其中\(x\)是自变量，\(y\)是\(x\)的函数。
没有什么问题，但是想要指出一点：
反比例函数写作\(y=\frac k x\)而不写作\(xy=k\)的原因在于\(x\)是自变量，一般放在等式的右边。
另外课本提出：
反比例函数的自变量\(x\)的取值范围是不等于\(0\)的一切实数（非\(0\)全体实数）。
以后写反比例函数时，不再强调\(k为常数，k\neq 0\)，也不强调\(x\neq 0\)。
图像
不得不承认，课本对反比例函数图像的探索十分肤浅（苏科版为例）：
列表：恰当地选取自变量\(x\)的几个值，计算函数\(y\)对应的值。
描点：以表中各对\(x\)、\(y\)的值为点的坐标，在平面直角坐标系中描出相应的点。
连线：用平滑的曲线顺次连接第一象限内的各点，得到图像的一支；顺次连接第三象限内的各点，得到图像的另一支。两支合在一起这就是反比例函数\(y=\frac k x\)的图像。
"列表"和"描点"步骤没有问题，毕竟是仿照一次函数探索。但是这个"连线"的理论过于突兀，现对此做出补充。
为什么是"平滑的曲线"？
以反比例函数\(y=\frac 6 x\)为例，我们找到了一些自变量\(x\)的值和对应的函数\(y\)的值：
| \(x\) | \(1\) | \(2\) | \(3\) | \(6\) |
|---|---|---|---|---|
| \(y\) | \(6\) | \(3\) | \(2\) | \(1\) |
并在平面直角坐标系中描出了点：
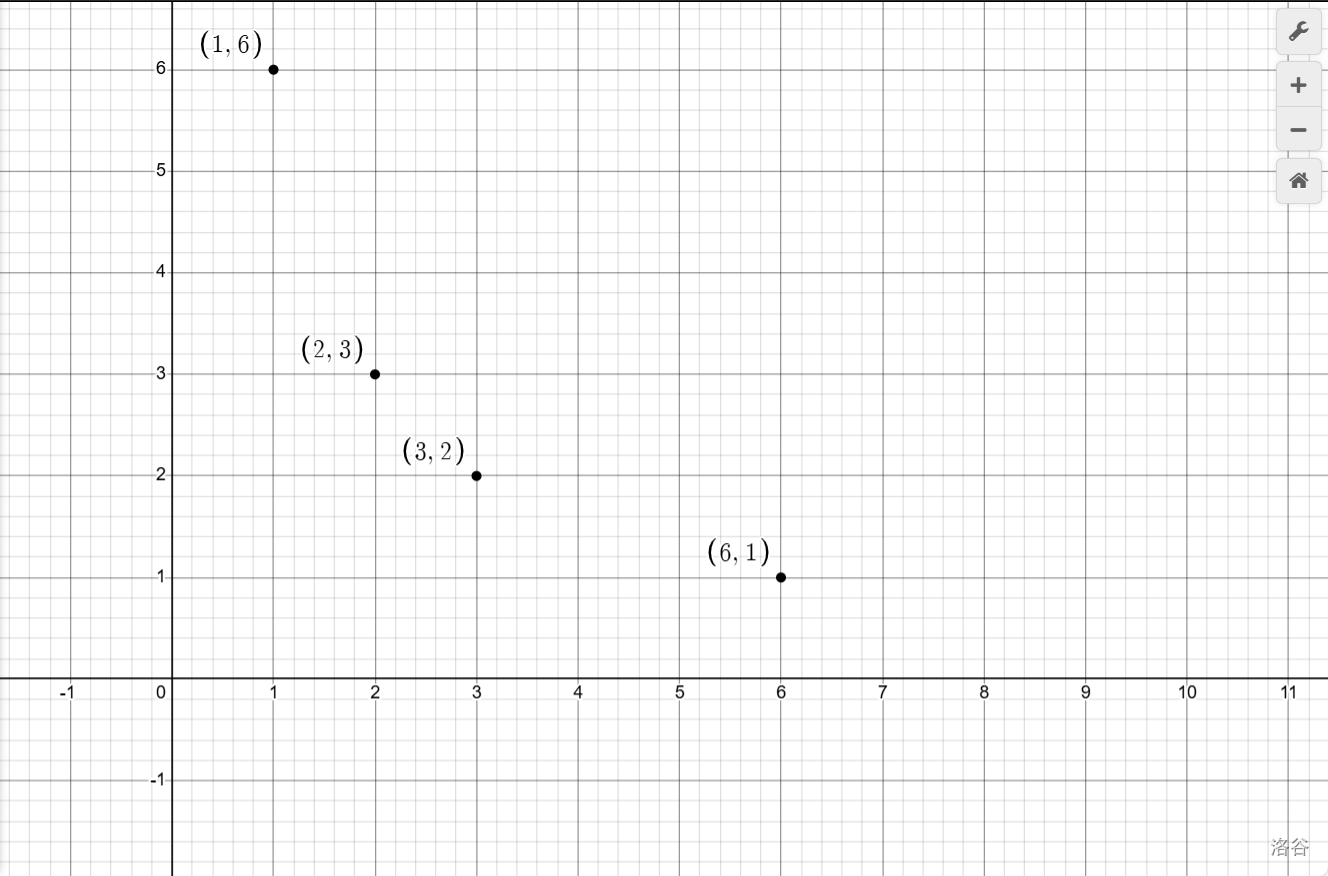
那问题来了：我为什么一定要认为该函数图像是一条平滑的曲线呢？为什么图像不能是这样：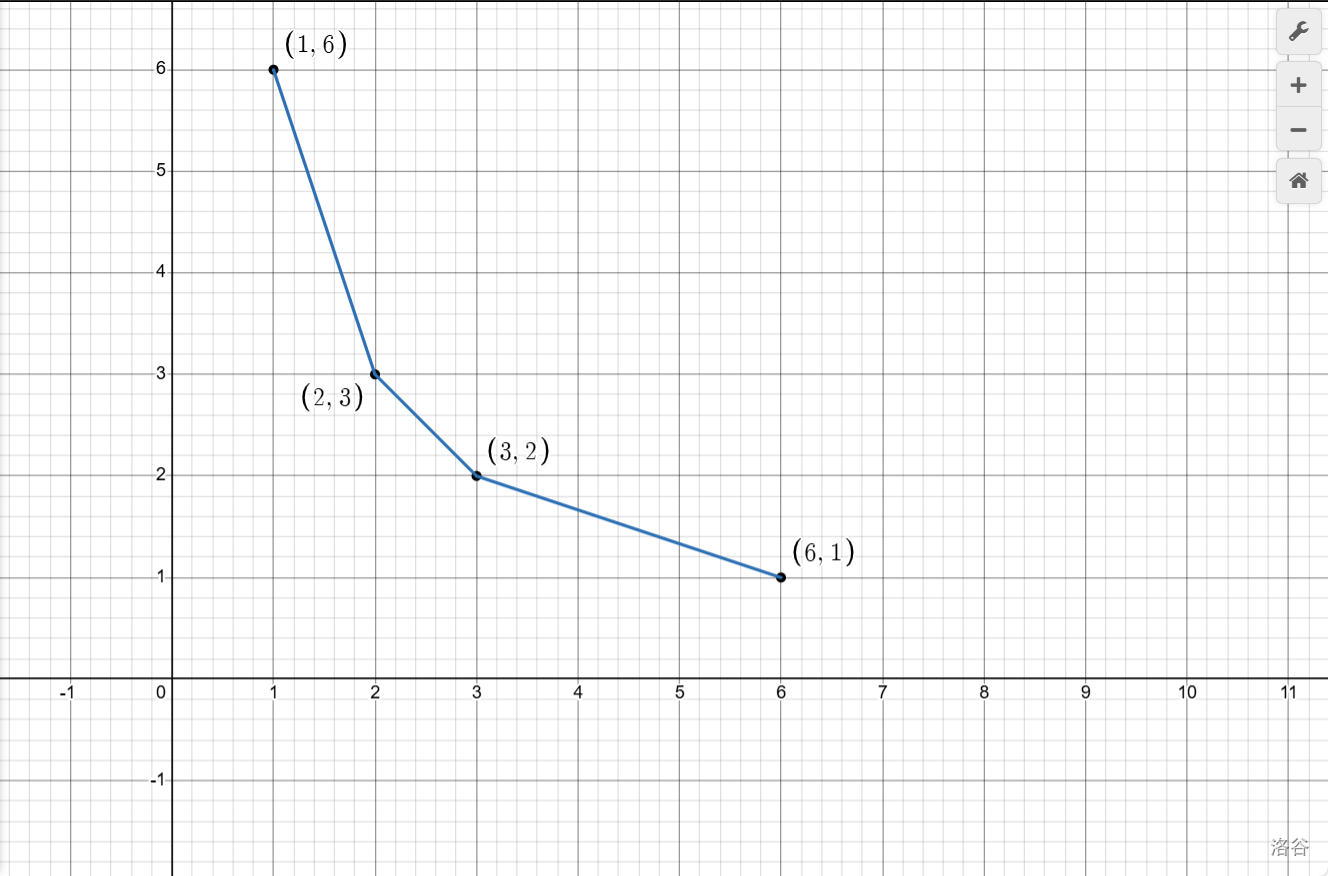
这样：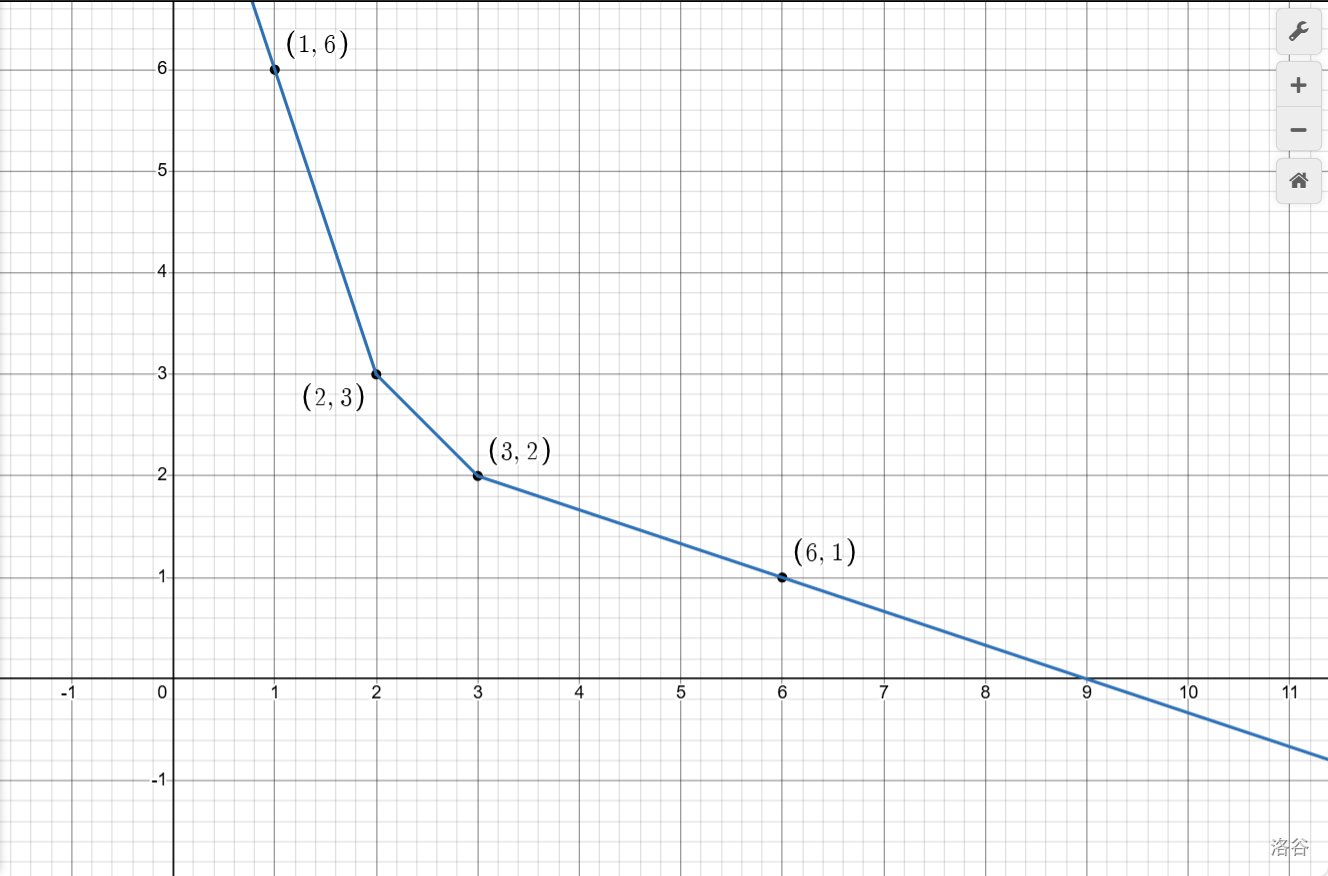
抑或是这样？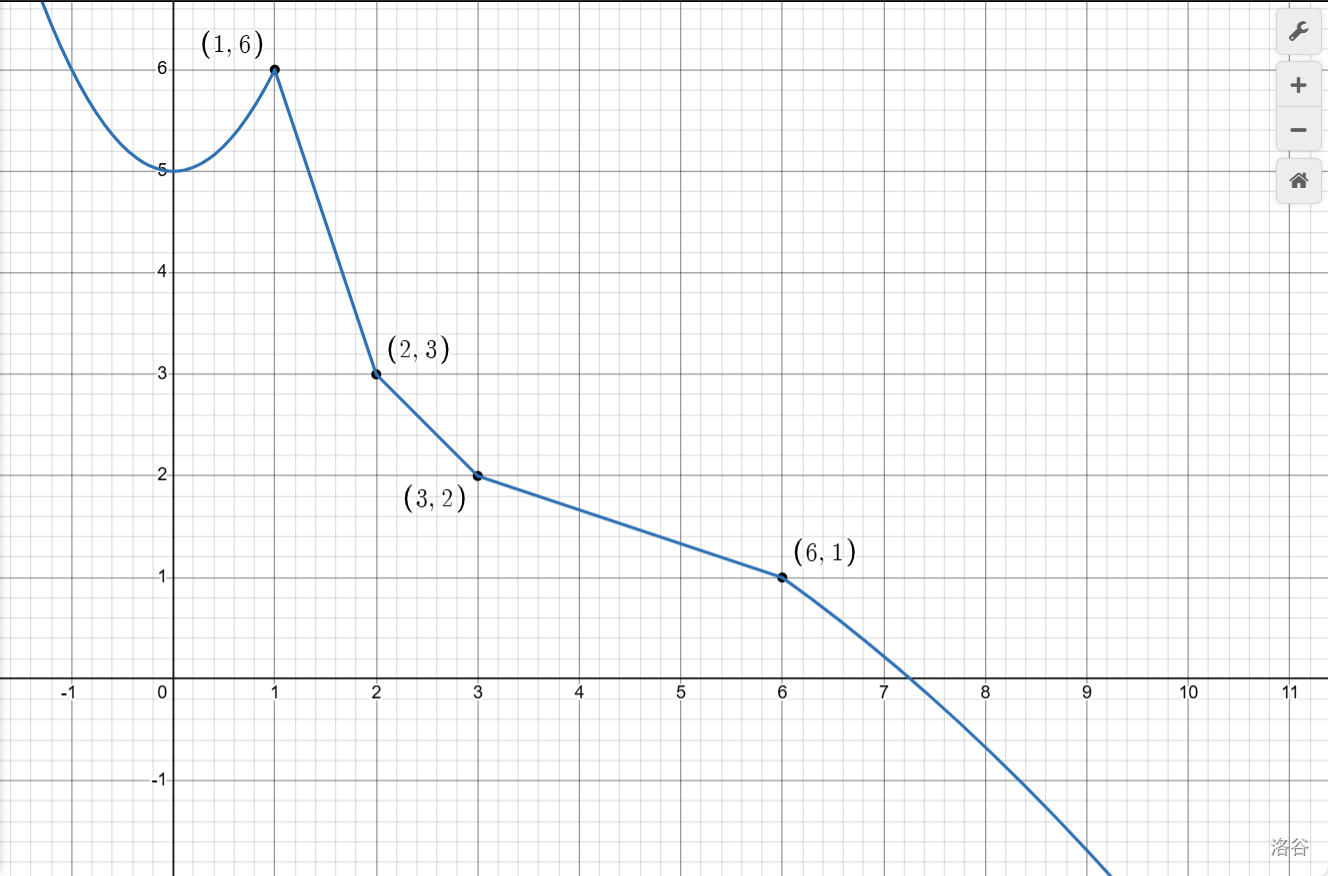
其中，函数\(x<1\)的部分是\(y=x^2+5 \{x<1\}\)，函数\(x>6\)的部分是\(y=\frac {114514} {1919810}x+\frac {6042314} {1919810}\{x>6\}\)，正好经过\((6,1)\)呢？
好了好了，我们不玩梗，认真探讨一下反比例函数的图像为什么是平滑的曲线？
关联：一次函数
应该没有人不知道一次函数的图像是一条直线 吧？那我们是如何证明的呢？
我们可以从证明一次函数上任意的三点共线 切入。
设在一次函数\(y=kx+b\)的图像上存在三个点\(A(x_1, kx_1+b)\)，\(B(x_2, kx_2+b)\)，\(C(x_3, kx_3+b)\)，且规定\(x_1<x_2<x_3\)。
方法1：证明\(AB+BC=AC\)。（命题①）
（命题②）
\[{AB}^2=(x_1-x_2)^2+[(kx_1+b)-(kx_2+b)]^2=(x_1-x_2)^2+(kx_1-kx_2)^2=(x_1-x_2)^2+k^2(x_1-x_2)^2=(k^2+1)(x_1-x_2)^2 \]
\[\therefore AB=(x_1-x_2)\sqrt{k^2+1} \]
\[{BC}^2=(x_2-x_3)^2+[(kx_2+b)-(kx_3+b)]^2=(x_2-x_3)^2+(kx_2-kx_3)^2=(x_2-x_3)^2+k^2(x_2-x_3)^2=(k^2+1)(x_2-x_3)^2 \]
\[\therefore BC=(x_2-x_3)\sqrt{k^2+1} \]
\[{AC}^2=(x_1-x_3)^2+[(kx_1+b)-(kx_3+b)]^2=(x_1-x_3)^2+(kx_1-kx_3)^2=(x_1-x_3)^2+k^2(x_1-x_3)^2=(k^2+1)(x_1-x_3)^2 \]
\[\therefore AC=(x_1-x_3)\sqrt{k^2+1} \]
\[\because AB+BC=(x_1-x_2)\sqrt{k^2+1}+(x_2-x_3)\sqrt{k^2+1}=(x_1-x_3)\sqrt{k^2+1} \]
\[AC=(x_1-x_3)\sqrt{k^2+1} \]
\[\therefore AB+BC=AC \]
命题得证。
方法2：证明\(\angle{ABC}=180 \degree\)。（命题③）
如图所示。图中的坐标仅供参考。根据我们所设，易得\(BM=kx_2-kx_1\)，\(AM=x_2-x_1\)；\(CN=kx_3-kx_2\)，\(BN=x_3-x_2\)。
\[在\triangle ABM和\triangle BCN中 \]
\[\left\{ \begin{aligned} &\frac {AM} {BN}=\frac {x_2-x_1} {x_3-x_2} \\ &\angle AMB= \angle BNC\\ &\frac {BM} {CN}=\frac {kx_2-kx_1} {kx_3-kx_2}=\frac {x_2-x_1}{x_3-x_2} \end{aligned} \right. \]
\[\therefore \triangle ABM ∽ \triangle BCN(SAS) \]
\[\therefore \angle ABM=\angle BCN \]
\[\because \angle BCN + \angle CBN=90\degree \]
\[\therefore \angle ABM+\angle CBN=90\degree \]
\[又\because \angle MBN=90\degree \]
\[\therefore \angle ABC=\angle ABM+\angle CBN+\angle MBN=180\degree \]
命题得证。
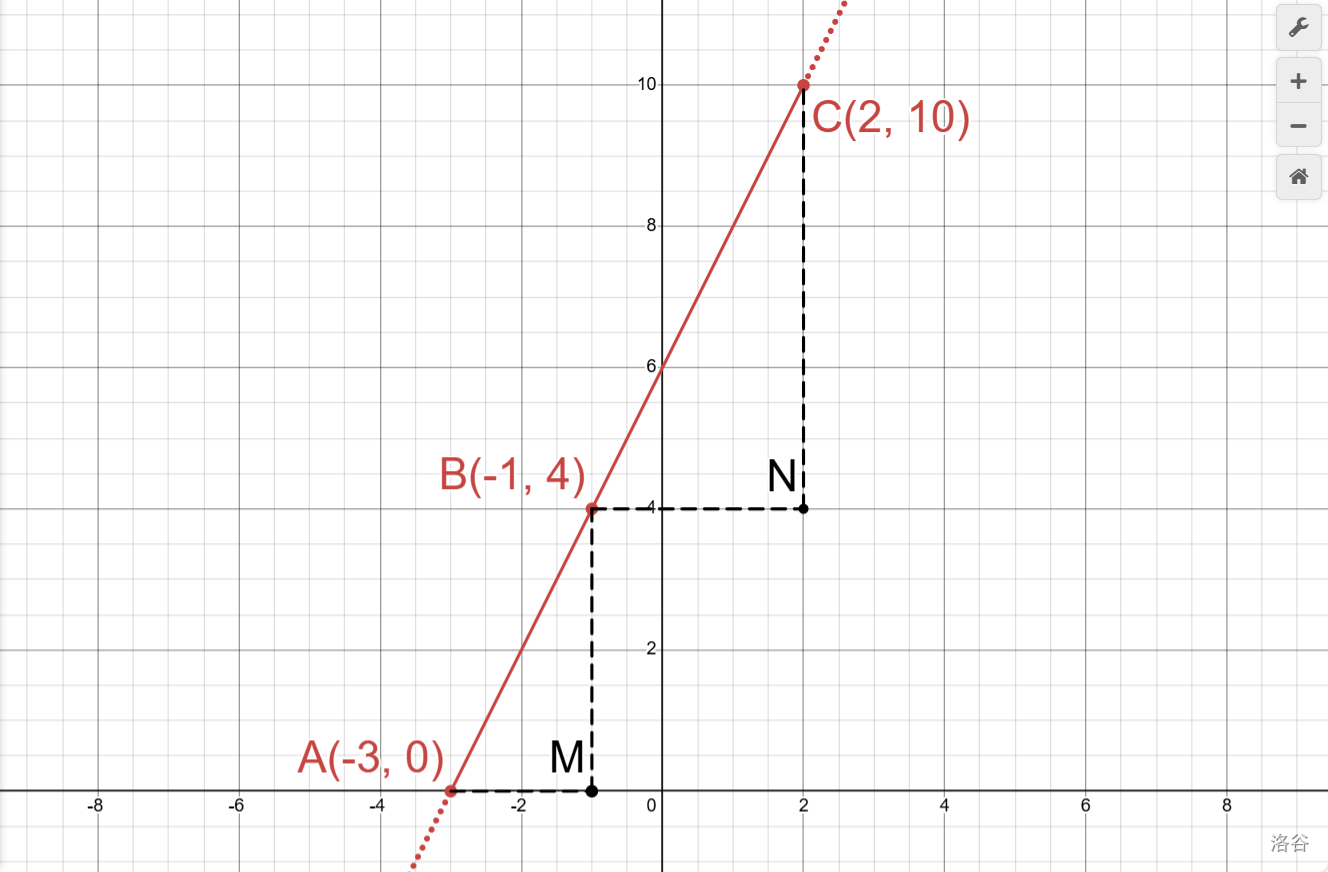
方法3：在一次函数不可用。会导致循环论证。
真正的证明
关联结束。现在，让我们用一次函数的方法来证明反比例函数图像是曲线（反比例函数图像上的任意三个点不共线）。
设在反比例函数\(y=\frac k x\)的图像上存在三个点\(A(a, \frac k a)\)，\(B(b, \frac k b)\)，\(C(c, \frac k c)\)，且规定\(a<b<c\)。
方法1：证明\(AB+BC\neq AC\)。（命题①）
这个方法超出初二年级可以理解的知识范围，感兴趣的朋友可以自证一下，这里不做展示。如果要写全过程的话我都要寄了。
方法2：证明\(\angle ABC \neq 180\degree\)。（命题③）
其实很简单，还按照刚刚的方法建立模型：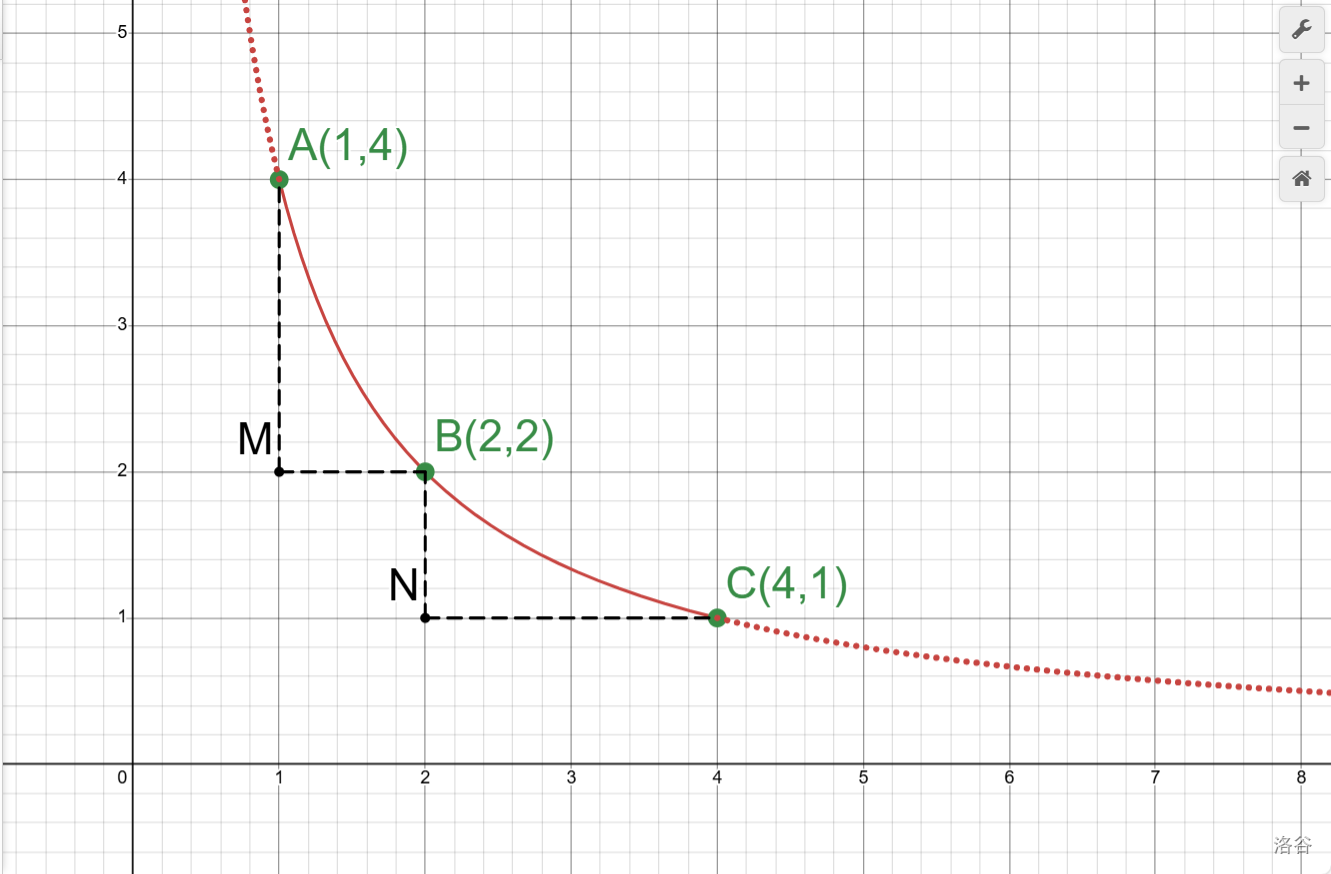
假设\(\angle ABC = 180\degree\)。根据刚刚的过程反推出：\(\angle ABM=\angle BCN\)。
\[在\triangle ABM和\triangle BCN中 \]
\[\left\{ \begin{aligned} &\angle ABM=\angle BCN \\ &\angle AMB= \angle BNC\\ \end{aligned} \right. \]
\[\therefore \triangle ABM ∽ \triangle BCN(AA) \]
\[\therefore \frac {AM} {BN}=\frac{BM}{CN} \]
\[\therefore \frac {\frac k a-\frac k b}{\frac k b-\frac k c}=\frac {b-a}{c-b} \]
\[\therefore \frac {\frac k {ab}\cdot (b-a)}{\frac k {bc}\cdot (c-b)}=\frac {(b-a)}{(c-b)} \]
\[\therefore \frac {\frac k {ab}}{\frac k {bc}}=1 \]
\[\therefore \frac k {ab}=\frac k {bc} \]
\[\therefore ab=bc, a=c \]
\[这与已知条件a<c矛盾 \]
\[\therefore 假设不成立 \]
命题得证。
方法3：证明\(k_{AB}\neq k_{AC}\)。（命题④）
这个方法在一次函数中确实不能用，因为计算\(k_{AB}\)就代表已经默认了一次函数图像是一条直线。但是这在反比例函数中就很好用：
令存在一条直线同时过\(A\)、\(B\)两点，则有：
\[k_{AB} = \frac {y_A-y_B} {x_A-x_B} = \frac {\frac k a - \frac k b} {a - b}=\frac {-\frac {(a-b)k} {ab}} {a-b}=-\frac k {ab} \]
又存在一条直线同时过\(A\)、\(C\)两点，则有：
\[k_{AC} = \frac {y_A-y_C} {x_A-x_C} = \frac {\frac k a - \frac k c} {a - c}=\frac {-\frac {(a-c)k} {ac}} {a-c}=-\frac k {ac} \]
\[\because b \neq c \]
\[\therefore ab \neq ac \]
\[\therefore -\frac k {ab} \neq -\frac k {ac} \]
\[\therefore k_{AB} \neq k_{AC} \]
命题得证。
需要说明的是，教材上只要求大家观察发现，但是证明的过程其实非常重要，因为这可以帮助理解反比例函数的各个基本结论，锻炼数形结合的能力，同时在应用方面也有很大的功效。
为什么有两支？
其实这个问题在课本中有暗示。
思考： 以反比例函数表达式\(y=\frac k x\)为例：
（1）\(x\)、\(y\)的值可以为\(0\)吗？这个函数的图像与\(x\)轴、\(y\)轴有交点吗？
（2）\(x\)、\(y\)所取值的符号有什么关系？这个函数的图像会在哪几个象限？
（3）......
那我们就逐一回答这些问题。
\(x\)、\(y\)的值不能为\(0\)。这个函数的图像与\(x\)轴、\(y\)轴没有交点。
\(x\)、\(y\)在\(k>0\)时同号，在\(k<0\)时异号。这个函数的图像在\(k>0\)时位于第一（三）象限，在\(k<0\)时位于第二（四）象限。
因此，你明白反比例函数的图像为什么有两支了吗？
首先，不经过相邻的象限，就已经将图像限定为了两种情况。 第一是这样：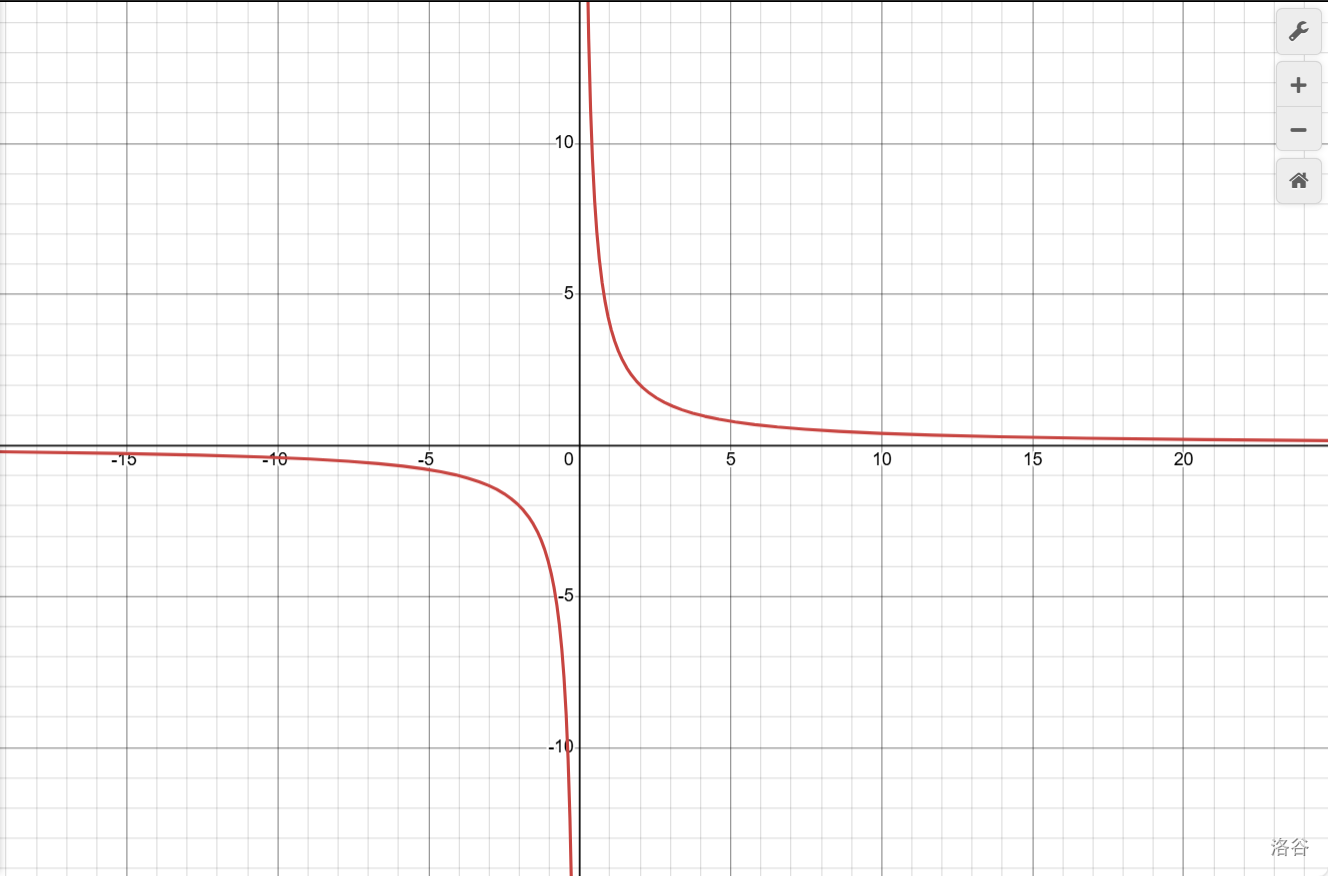
第二是这样：
有点像两个人牵手
但是，第二个条件限制图像不能与\(x\)、\(y\)轴有交点，排除了牵手第二种情况。那么，这两支图像根本没法牵手就只能分为两支了。
补充：反比例函数图像的每一支在\(x\)趋向于\(\infty\)时趋向于\(0\)，在\(x\)趋向于\(0\)时趋向于\(\infty\)。但\(x\)、\(y\)都无法到达\(0\)，这也是极限思想所强调的（无限逼近但无法到达）。即：
\[\lim_{x \to 0}y=\infty, \lim_{x \to \infty}y=0 \]
图像性质
研究一次函数图像的性质时，我们研究：
\[\left\{ \begin{aligned} &增减性（又称单调性）； \\ &对称性；\\ &最值（函数的最高点和最低点，又称值域）。\\ \end{aligned} \right. \]
那么，我们类比研究一下反比例函数。
增减性（单调性）
有一个反比例函数\(y=\frac k x\)前来买瓜。
提醒：在解题时，应该注意问题的多解性和多种情况。
情况\(1\)：\(k>0\)
设在反比例函数\(y=\frac k x\{ k>0 \}\)的任一半支上存在两个点\(A(a, \frac k a)\)、\(B(b, \frac k b)\)，且\(a< b\)。
则：
\[\frac k a - \frac k b = \frac {bk-ak} {ab} = -(a-b) \cdot \frac k {ab} \]
\[\because a、b位于反比例函数图像的同一支 \]
\[\therefore ab>0 \]
\[\because a-b<0, ab>0, k>0 \]
\[\therefore -(a-b) \cdot \frac k {ab}>0 \]
\[\therefore \frac k a > \frac k b \]
\[又\because a<b \]
因此，反比例函数\(y=\frac k x\{k>0\}\)的每一支上，都有\(y\)随\(x\)的增大而减小。
情况\(2\)：\(k<0\)
设在反比例函数\(y=\frac k x\{ k>0 \}\)的任一半支上存在两个点\(A(a, \frac k a)\)、\(B(b, \frac k b)\)，且\(a< b\)。
则：
\[\frac k a - \frac k b = \frac {bk-ak} {ab} = -(a-b) \cdot \frac k {ab} \]
\[\because a、b位于反比例函数图像的同一支 \]
\[\therefore ab>0 \]
\[\because a-b<0, ab>0, k<0 \]
\[\therefore -(a-b) \cdot \frac k {ab}<0 \]
\[\therefore \frac k a < \frac k b \]
\[又\because a<b \]
因此，反比例函数\(y=\frac k x\{k<0\}\)的每一支上，都有\(y\)随\(x\)的增大而增大。
综上所述：
对于一个反比例函数\(y=\frac k x\)：
- 当\(k>0\)，\(y\)随\(x\)的增大而减小；
- 当\(k<0\)，\(y\)随\(x\)的增大而增大。
对称性
再次提醒：在解题时，应该注意问题的多解性和多种情况。
\(I)\) 中心对称性
课本上让大家尝试得出结果：
在图中，画点\(A(4, -2)\)，点\(A\)在函数\(y=-\frac 8x\)的图像上吗？写出点\(A\)关于原点\(O\)对称的点\(A'\)的坐标，点\(A'\)在函数\(y=-\frac 8x\)的图像上吗？在函数\(y=-\frac 8x\)的图像上任取一点\(B\)，点\(B\)关于原点\(O\)的对称点\(B'\)在这个图像上吗？
反比例函数的两支图像关于原点对称。
虽然够随机，够普遍，但我们仍然证明一把：
证明：反比例函数的两支图像关于原点对称。
设在反比例函数\(y=\frac k x\)的图像上有一点\(P(t, \frac k t)\)。由命题⑤可得，点\(P\)关于原点的对称点\(P'\)坐标为\((-t, -\frac k t)\)。此时我们需要证明\(P'\)在反比例函数图像的另一支上。
很简单：当\(x=-t\)时，\(y=\frac k {-t}=-\frac k t\)。
\[\because -\frac k t = -\frac k t \]
\[\therefore 点P'在反比例函数y=\frac k x图像的另一支上。 \]
位于反比例函数图像的两支上的两个对应点\(P\)和\(P'\)关于原点对称。
同理可证其它点。
命题得证。
\(II)\) 轴对称性
嗯？课本上没讲？
我们可不管，没讲我们要自己探索。
几何最重要的是"形感"。其实，那些"注意力惊人"的人靠的就是"数感"和"形感"。有了形感，你才能发现结论，从而才能从另一方向证明。有的时候，证明远比得出结论简单。
证明\(1\)：反比例函数图像关于直线\(y=x\)对称。
设在反比例函数\(y=\frac k x\)的图像上有一点\(P(t, \frac k t)\)。由命题⑧可得，点\(P\)关于直线\(y=x\)的对称点\(P'\)坐标为\((\frac k t, t)\)。 类比中心对称性，证明\(P'\)在反比例函数图像上。
当\(x=\frac k t\)时，\(y=\frac k {\frac k t}=t\)。
\[\because t=t \]
\[\therefore 点P'在反比例函数y=\frac k x图像上。 \]
因此位于反比例函数图像上的两个对应点\(P\)和\(P'\)关于直线\(y=x\)对称。
同理可证其它点。
命题得证。
证明\(2\)：反比例函数图像关于直线\(y=-x\)对称。
设在反比例函数\(y=\frac k x\)的图像上有一点\(P(t, \frac k t)\)。由命题⑨可得，点\(P\)关于直线\(y=-x\)的对称点\(P'\)坐标为\((-\frac k t, -t)\)。 类比中心对称性，证明\(P'\)在反比例函数图像上。
当\(x=-\frac k t\)时，\(y=\frac k {-\frac k t}=-t\)。
\[\because -t=-t \]
\[\therefore 点P'在反比例函数y=\frac k x图像上。 \]
因此位于反比例函数图像上的两个对应点\(P\)和\(P'\)关于直线\(y=-x\)对称。
同理可证其它点。
命题得证。
综上所述：
对于一个反比例函数\(y=\frac k x\)的图像，
- 它关于原点对称。
- 它关于直线\(y=x\)和\(y=-x\)对称。
最值（值域）
这个反而最简单？
对于一个反比例函数\(y=\frac k x\)，
- \(x\)的值域为\((-\infty, 0) \& (0, +\infty)\)
- \(y\)的值域为\((-\infty, 0) \& (0, +\infty)\)
即：
- \(x\)的最大值为\(+\infty\)（不取），最小值为\(-\infty\)（不取）且\(x\neq 0\)。
- \(y\)的最大值为\(+\infty\)（不取），最小值为\(-\infty\)（不取）且\(y\neq 0\)。
图像随\(k\)的变化情况
让函数动起来通常是考试区分中优等生的方法。而最简单的途径就是------加参数。
幸好，反比例函数有且只有一个参数：\(k\)。那让我们研究反比例函数图像随\(k\)的变化情况吧。
（参见苏科版八年级下册教材\(P133-134\)）打开计算机函数软件，在左侧的表达式框中输入\(y=\frac k x\)（依次按下\(y=k/x\)）。单击弹出的"添加滑块"后的"\(k\)"键。单击弹出的滑块的"播放"键，观察右侧函数图像随\(k\)的变化。
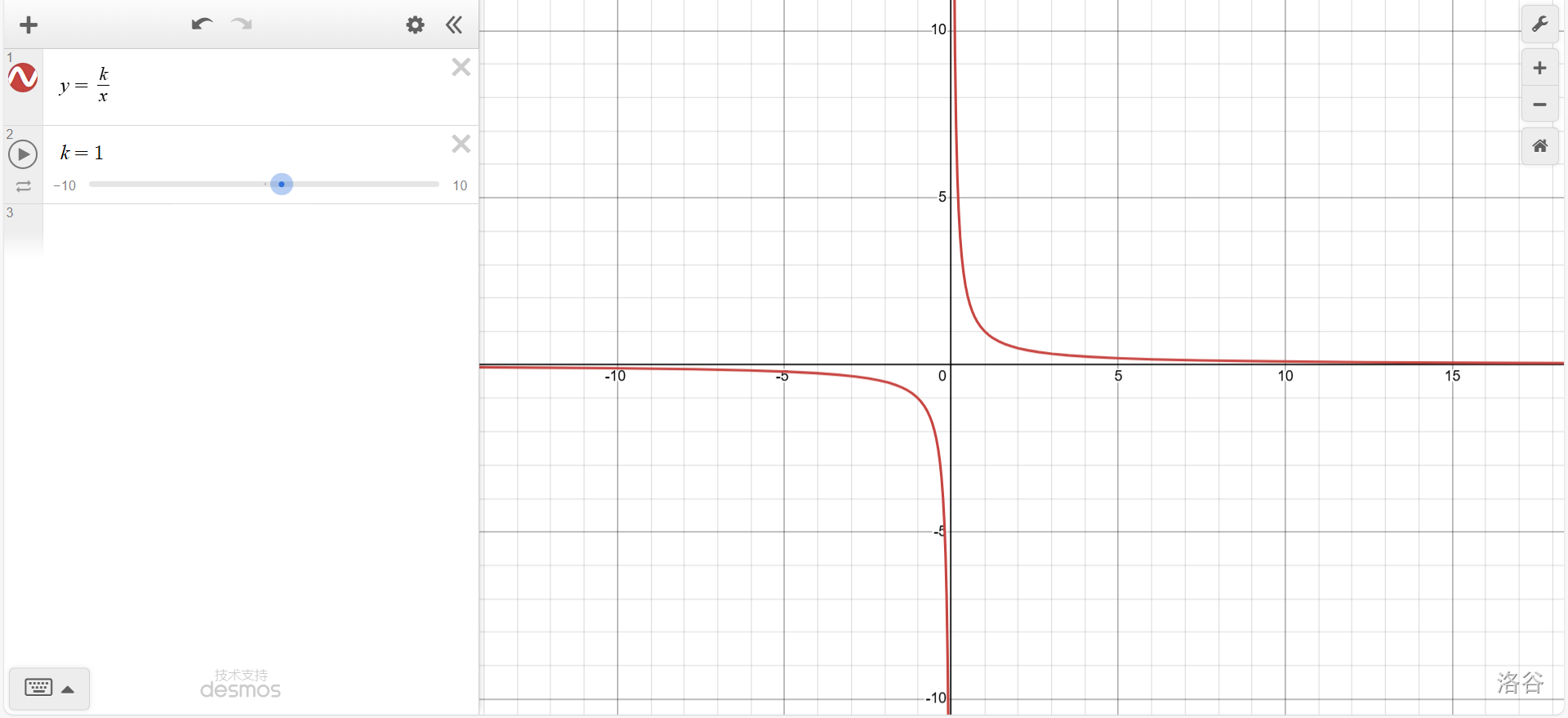
可以看出，\(|k|\)越大，双曲线上与原点距离最近的一点（即反比例函数\(y=\frac k x\)与正比例函数\(y=x\)的交点）与原点的距离越远。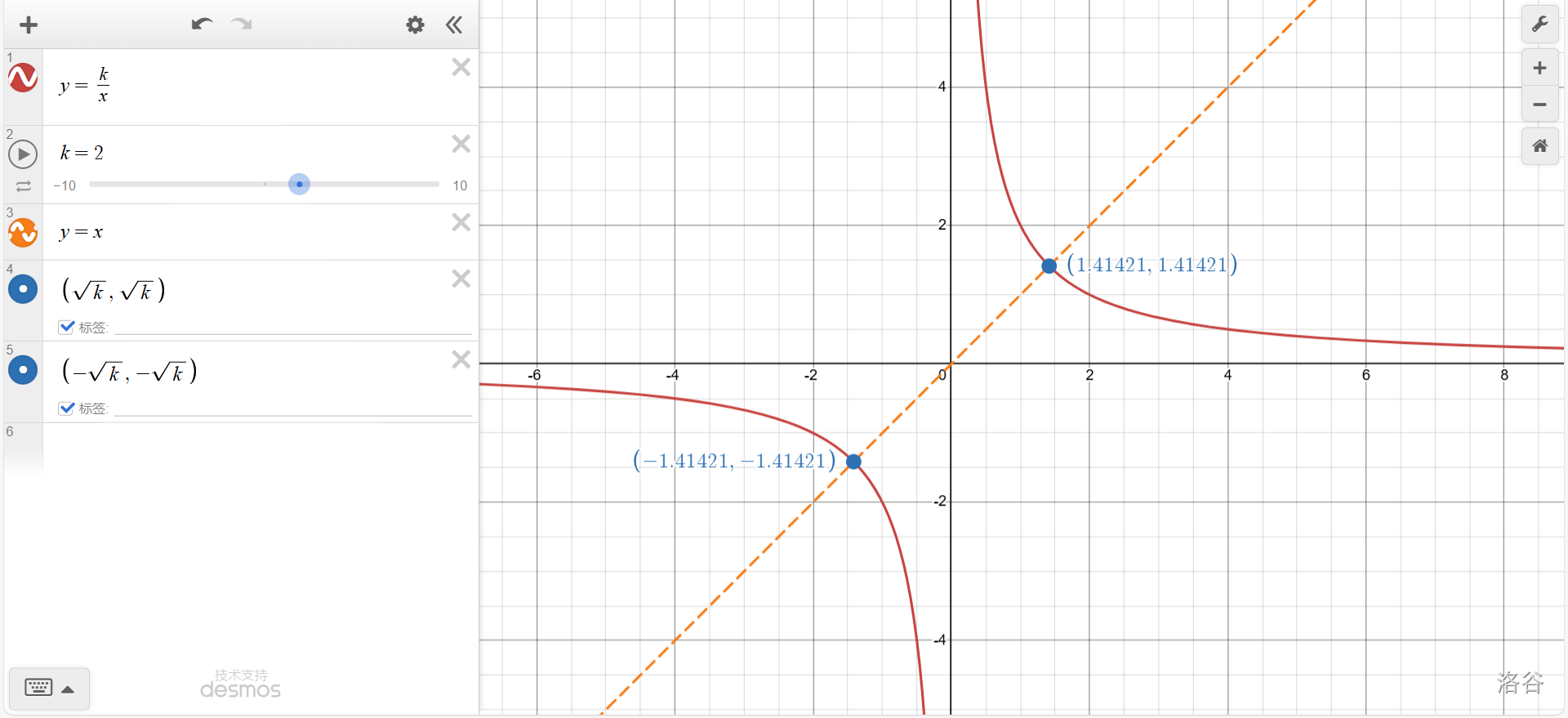
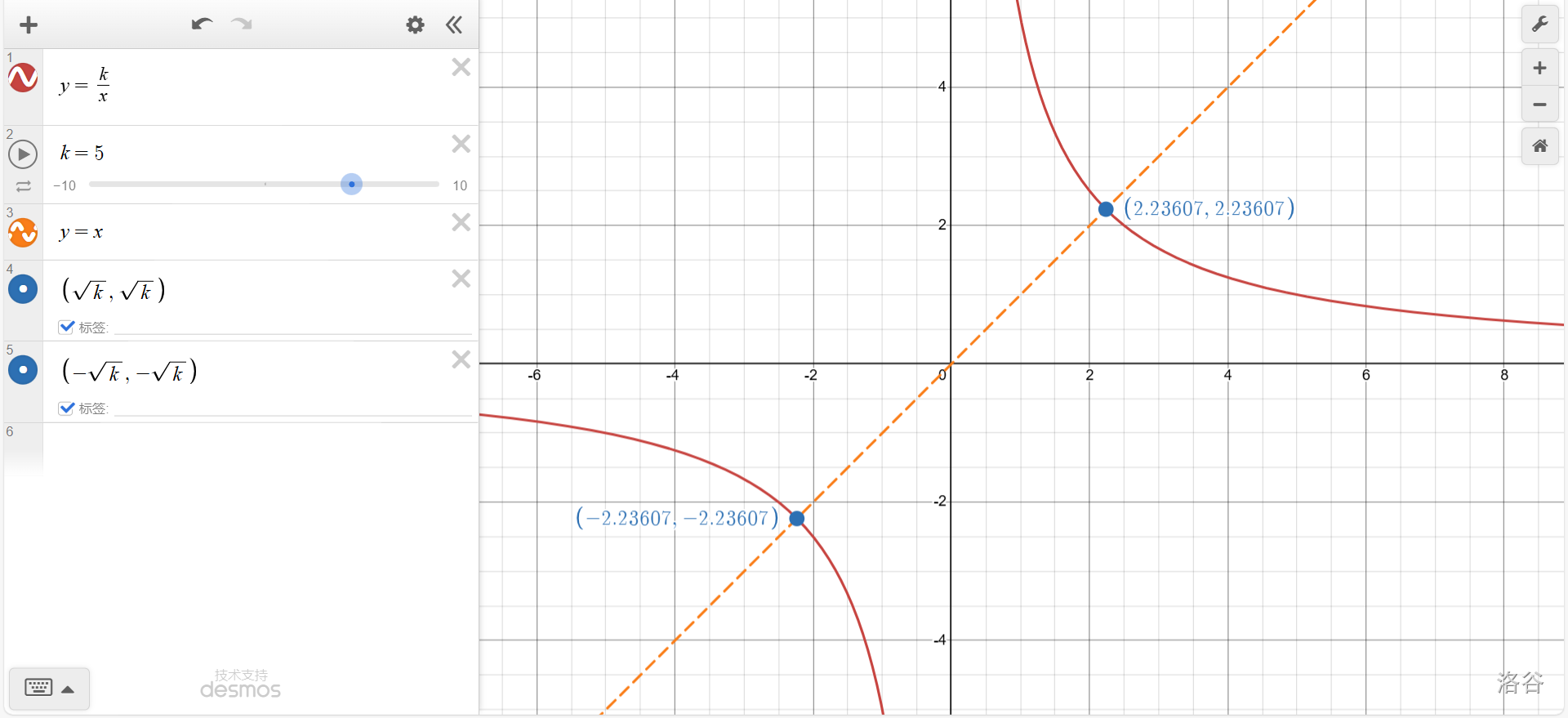
证明非常简单，只需要求出交点坐标到原点的距离就行了。已知交点\(P\)坐标为二元方程组\(\left\{ \begin{aligned} &y=\frac k x\\ &y=x \end{aligned}\right.\)的解\(\left\{ \begin{aligned} &x=±\sqrt k\\ &y=±\sqrt k \end{aligned}\right.\)。其到原点的距离\(d_{OP}=\sqrt {(±\sqrt k)^2+(±\sqrt k)^2}=\sqrt {2k}\)。（命题②）很明显，\(d_{OP}=\sqrt {2k}\)是一个根式函数，其值随\(k\)的增大而增大。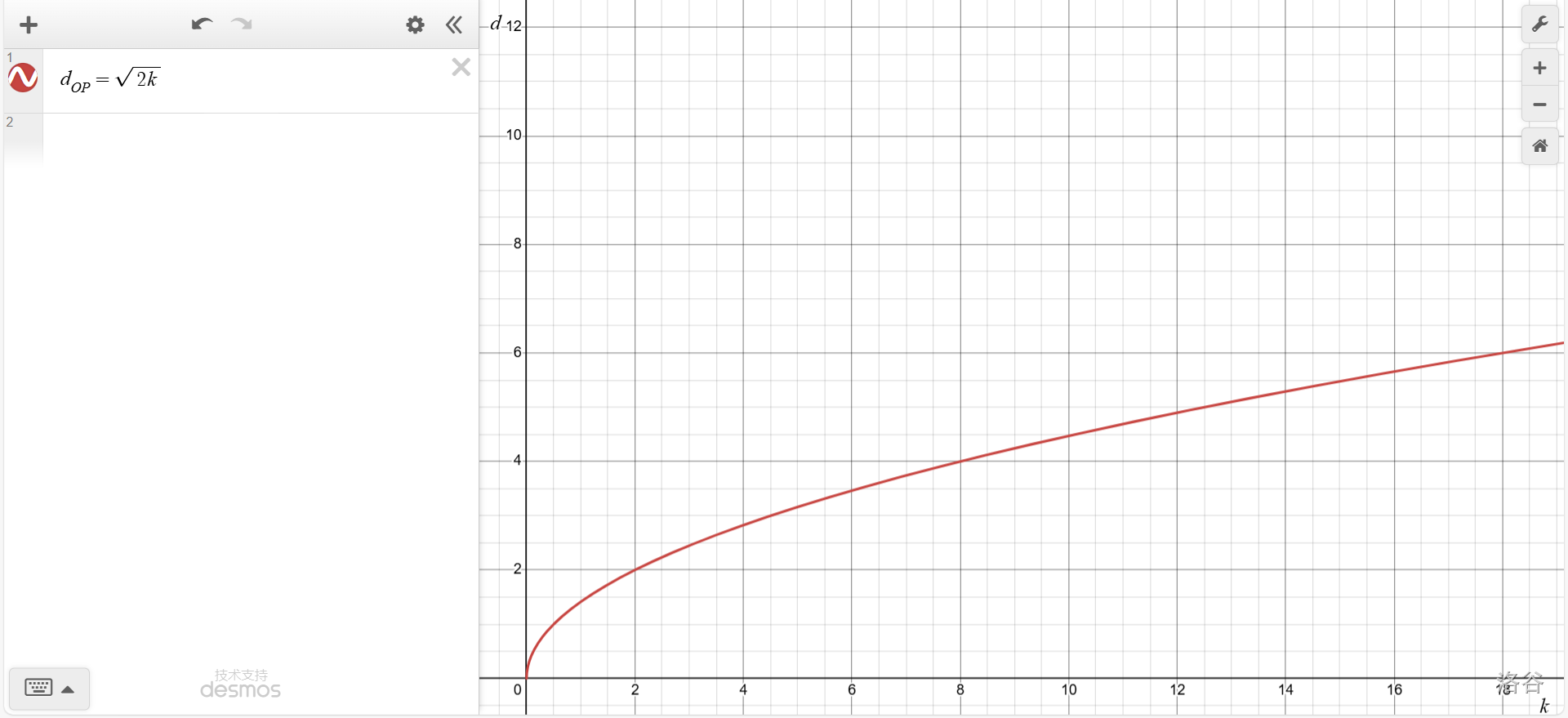
附上证明：\((±\sqrt k, ±\sqrt k)\)为反比例函数图像上距离原点最近的一点。
设在反比例函数\(y=\frac k x\)的图像上有一点\(P(t, \frac k t)\)，\(t>0\)。已知：
\[d_{OP}^2=t^2+(\frac k t)^2 \]
\[\begin{aligned} 注意到(t+\frac k t)^2&=t^2+(\frac k t)^2+2t\cdot \frac k t\\ &=d_{OP}^2+2k \end{aligned}\]
\[\begin{aligned} \therefore (d_{OP}^2){min}&=[(t+\frac k t)^2]{min}-2k \\ &=[(t+\frac k t)_{min}]^2-2k （命题⑩）\end{aligned} \]
\[由基本不等式（均值定理）得： \]
\[\begin {aligned}\frac {t+\frac k t} 2 &\geq \sqrt{t\cdot \frac k t}=\sqrt k\\t+\frac k t &\geq 2\sqrt k \\当且仅当t&=\frac k t时，\\ (t+\frac k t)_{min}&=2\sqrt k \\ t&=\frac k t=\sqrt k\end {aligned} \]
\[因此，当且仅当t=\frac k t =\sqrt k时， \]
\[(t+\frac k t){min}=2\sqrt k，(d{OP}^2)_{min}=2k \]
\[\begin {aligned} \therefore 当且仅当t=\frac k t&=\sqrt k时，\\(d_{OP}){min}=\sqrt {(d{OP}^2)_{min}}&=\sqrt {2k}（命题⑩） \end {aligned} \]
\[同理在t<0时也成立。 \]
命题得证。
以上就是反比例函数的所有基础内容及其证明了，希望这篇文章对你学习反比例函数有所帮助。下期预告：反比例函数的深层理解和应用。