如同正整数的截是有限集的样本那样，所有正整数的集合\(\mathbb{Z}_+\)就是可数无限集的样板。本节将研究这种集合，还要构造一些既不是有限集也不是可数无限集的集合。这种研究将引导我们去讨论"归纳定义"过程的含义。
定义 一个集合\(A\)称为无限的 （infinite），如果它不是有限集。一个无限集\(A\)称为可数无限的（countably infinite），如果存在一个一一对应
\[f:A\longrightarrow \mathbb{Z}_+ \]
定义 一个集合称为可数的 （countable），如果它是有限集或者可数无限集。一个集合不是可数的，就称为不可数的（uncountable）。
以下定理为我们提供了一个判定集合可数性的常规方法。
定理 7.1 设\(B\)是一个非空集，则下列条件等价：
(1) \(B\)是可数集；
(2) 存在一个满射\(f:\mathbb{Z}_+\rightarrow B\)；
(3) 存在一个单射\(g:B\rightarrow\mathbb{Z}_+\)。
证明 (1)\(\Rightarrow\)(2)。设\(B\)是一个可数集，如果\(B\)是可数无限集，则根据定义存在一个一一对应\(f:\mathbb{Z}+\rightarrow B\)，从而结论成立。如果\(B\)是一个有限集，则对于某一个\(n\ge 1\)，存在一个一一对应\(h:\{1,\cdots,n\}\rightarrow B\)（注意\(B\ne \varnothing\)），可以把\(h\)扩张为一个满射\(f:\mathbb{Z}+\rightarrow B\)，其定义为
\[f(i)= \begin{cases} h(i),&1\leqslant i \leqslant n,\\ h(1),&i>n. \end{cases} \]
从而结论成立。
(2)\(\Rightarrow\)(3)。设\(f:\mathbb{Z}+\rightarrow B\)是一个满射。\(g:B\rightarrow \mathbb{Z}+\)定义为：
\[g(b)=f^{-1}(\{b\})\text{的最小元} \]
因为\(f\)是一个满射，\(f^{-1}(\{b\})\)非空，所以\(g\)的定义是确切的。如果\(b\ne b'\)，集合\(f^{-1}(\{b\})\)与\(f^{-1}(\{b'\})\)无交，它们的最小元不同，因此\(g\)是一个单射。
(3)\(\Rightarrow\)(1)。设\(g:B\rightarrow \mathbb{Z}+\)是一个单射，我们要证明\(B\)是一个可数集。通过改变\(g\)的值域可以得到\(B\)与\(\mathbb{Z}+\)的一个子集之间的一个一一对应。因此只要证明\(\mathbb{Z}+\)的任意子集是可数的，便可以证明结论。令\(C\)为\(\mathbb{Z}+\)的一个子集。
如果\(C\)是一个有限集，根据定义它是可数的。因此，我们只需证明\(\mathbb{Z}+\)的无限子集\(C\)是一个可数无限集。这个论断是容易理解的。事实上，我们可以将\(C\)的元素排列成一个无穷序列，这只需将\(\mathbb{Z}+\)的元素先按通常的顺序排列，然后再"删除"\(\mathbb{Z}_+\)中所有不在\(C\)中的元素。
以上陈述仅是对证明的轮廓的一个直观说明，严格的证明还须细致的推理分析。我们将作为一个引理予以陈述。
\\square
引理 7.2 设\(C\)是\(\mathbb{Z}_+\)的一个无限子集，那么\(C\)是一个可数无限集。
证明 我们将构造一个一一对应\(h:\mathbb{Z}+\rightarrow C\)。采用归纳法。定义\(h(1)\)为\(C\)的最小元，由于\(\mathbb{Z}+\)的任意非空子集\(C\)有最小元，所以\(h(1)\)是存在的。假定\(h(1),\cdots,h(n-1)\)已有定义，我们定义
\[h(n)=[C-h(\{1,\cdots,n-1\})]\text{的最小元} \]
集合\(C-h(\{1,\cdots,n-1\})\)是非空的，这是因为：如果它是空集的话，\(h:\{1,\cdots,n-1\}\rightarrow C\)便是一个满射，（根据推论 6.7）\(C\)就是一个有限集了。所以\(h(n)\)的定义是确切的。根据归纳法，对于所有\(n\in\mathbb{Z}_+\)，\(h(n)\)有定义。
容易证明\(h\)是一个单射，当\(m<n\)时，注意\(h(m)\)属于集合\(h(\{1,\cdots,n-1\})\)，根据定义\(h(n)\)不属于这个集合。因此\(h(n)\ne h(m)\)。
为了证明\(h\)是一个满射，令\(c\)为\(C\)的任意一个元素，我们证明\(c\)在\(h\)的像集中。首先注意到\(h(\mathbb{Z}+)\)不可能被包括在有限集\(\{1,\cdots,c\}\)中，这是由于\(h(\mathbb{Z}+)\)是无限集（\(h\)是单射）。因此在\(\mathbb{Z}+\)中有一个元素\(n\)，使得\(h(n)>c\)。令\(m\)是\(\mathbb{Z}+\)中满足\(h(m)\geqslant c\)的最小元，于是对于所有\(i<m\)，总有\(h(i)<c\)。所以\(c\)不属于集合\(h(\{1,\cdots,m-1\})\)。由于\(h(m)\)定义为集合\(C-h(\{1,\cdots,m-1\})\)的最小元，从而\(h(m)\leqslant c\)。两个不等式合起来就得到要证明的\(h(m)=c\)。
\\square
在上述定理的证明中，有一处用到了逻辑学的一个原理。当时我们说"根据归纳法"对所有正整数\(n\)定义了函数\(h\)。你可能以前见过这样的论证，并且当时不曾对它的合法性有所怀疑。
但这里有一个问题，毕竟归纳原理只表明：当\(A\)是包含正整数集的一个归纳集时，\(A=\mathbb{Z}+\)。在使用这个原理"根据归纳法"证明一个定理的时候，在一开始就说"设\(A\)是使得定理成立的所有正整数\(n\)的集合"，然后回过头来证明\(A\)为归纳集，从而\(A\)等于\(\mathbb{Z}+\)。可是，在上面的定理中，我们并没有真正用归纳法证明一个定理，而只是用它定义了一些东西。那么我们应该如何着手证明呢？能不能在开始时就说"令\(A\)是使函数\(h\)有定义的所有正整数\(n\)的集合"呢？那是不妥当的，因为在证明之初，符号\(h\)并没有意义。它的意义只是在证明的过程中才出现。因此，先定义一些东西就十分必要了。
这样我们就需要有另一个原理，称之为归纳定义原理（principle of recursive definition）。在前面一个定理的证明中，我们希望肯定下面的事实：
给定\(\mathbb{Z}+\)的无限子集\(C\)，存在唯一的函数\(h:\mathbb{Z}+\rightarrow C\)，满足条件：
\[\begin{aligned} &h(1)=C\text{的最小元}\\ &h(i)=[C-h(\{1,\cdots,i-1\})]\text{的最小元},\text{对于所有}i>1 \end{aligned} \]
该公式称为\(h\)的一个归纳公式 （recursion formula），它定义了函数\(h\)。根据这样的公式给出的定义称为归纳定义（recursive definition）。
在我们试图定义某件事的时候，就会遇到逻辑上的困难。并不是所有归纳公式都是有意义的。例如，归纳公式
\[h(i)=h(i)=[C-h(\{1,\cdots,i+1\})]\text{的最小元} \]
就自相矛盾。虽然\(h(i)\)必须属于集合\(h(\{1,\cdots,i+1\})\)，公式却说它不属于这个集合。下面这个例子也是经典的悖论：
塞尔维亚的理发师给塞尔维亚的每一个不给自己剃胡子的人剃胡子。那么谁给理发师剃胡子呢？
在这句话中，"理发师"出现了两次，一次在短语"塞尔维亚的理发师"中，另一次是作为"塞尔维亚人"集合中的一个成员，被理发师剃胡子的人的定义是归纳的。但这个定义是自相矛盾的。
然而，有些归纳公式是有意义的。特别地，有以下原理：
归纳定义原理 （principle of recursive definition） 设\(A\)是一个集合。给出一个公式：定义\(h(1)\)为\(A\)的唯一一个的元素。对于\(i>1\)定义\(h(i)\)为\(A\)的这样唯一一个的元素，它仅与\(h\)在小于\(i\)的正整数时的值有关，这个公式便决定了唯一的一个函数\(h:\mathbb{Z}_+\rightarrow A\)。
这就是我们在证明引理 7.2时实际用到的原理。如果读者愿意的话，可以直接相信它是对的。当然它也能用归纳原理加以严格证明。下节将给出精确的描述，并且指出如何予以证明。数学家们很少专门援引这个原理。他们更愿意像在引理 7.2的证明中那样，当确实要用到归纳定义原理时，再设法用"归纳原理"来定义一个函数。为了避免过于迂腐，本系列也遵从这个惯例。
推论 7.3 可数集的子集也是可数的。
证明 假定\(A\subset B\)，其中\(B\)是一个可数集。那么，存在一个从\(B\)到\(\mathbb{Z}+\)的单射\(f\)，而\(f\)在\(A\)上的限制即为从\(A\)到\(\mathbb{Z}+\)的一个单射。
\\square
推论 7.4 集合\(\mathbb{Z}+\times\mathbb{Z}+\)是可数无限的。
证明 根据定理 7.1，只要构造一个单射\(f:\mathbb{Z}+\times\mathbb{Z}+\rightarrow \mathbb{Z}_+\)，将\(f\)定义为
\[f(n,m)=2^n3^m \]
容易验证\(f\)是一个单射。假定\(2^n3^m=2^p3^q\)，当\(n<p\)时，有\(3^m=2^{p-n}3^q\)，这与\(3^m\)对于所有\(m\)都是奇数这一事实相矛盾，因此\(n=p\)，从而\(3^m=3^q\)。如果\(m<q\)，则\(1=3^{q-m}\)，又导致矛盾，因此\(m=q\)。
\\square
定理 7.5 可数集的可数并是可数的。
证明 设\(\{A_n\}{n\in J}\)为可数集的一个加标族，其指标集\(J\)为\(\{1,\cdots,N\}\)或\(\mathbb{Z}+\)。为方便起见，还假定每一个集合\(A_n\)非空------这种假定并不影响结论的一般性。
因为每一个\(A_n\)是可数的，故对每一个\(n\)可以选取一个满射\(f_n:\mathbb{Z}+\rightarrow A_n\)。类似地，可以选取一个满射\(g:\mathbb{Z}+\rightarrow J\)。用
\[h(k,m)=f_{g(k)}(m) \]
定义函数
\[h:\mathbb{Z}+\times\mathbb{Z}+\longrightarrow \bigcup_{n\in J}A_n \]
容易验证\(h\)是一个满射。因为\(\mathbb{Z}+\times\mathbb{Z}+\)与\(\mathbb{Z}_+\)之间有一个一一对应，根据定理 7.1即得出并的可数性。
\\square
定理 7.6 可数集的有限积是可数的。
证明 我们首先证明两个可数集\(A\)和\(B\)的积是一个可数集。若\(A\)或\(B\)是空集，结论显然成立。若\(A\)和\(B\)都不是空集，可选取两个满射\(f:\mathbb{Z}+\rightarrow A\)和\(g:\mathbb{Z}+\rightarrow B\)。于是用\(h(n,m)=(f(n),f(m))\)定义的函数\(h:\mathbb{Z}+\times\mathbb{Z}+\rightarrow A\times B\)是一个满射，因此\(A\times B\)是可数的。
以下对一般情形进行归纳。假定当每一个\(A_i\)可数时，\(A_1\times\cdots\times A_{n-1}\)可数，证明对于积\(A_1\times\cdots\times A_n\)同样的结论成立。
首先注意，存在一个用
\[g(x_1,\cdots,x_n)=((x_1,\cdots,x_{n-1}),x_n) \]
定义的一一对应
\[g:A_1\times\cdots\times A_n\longrightarrow (A_1\times\cdots\times A_{n-1})\times A_n \]
因为根据归纳假定\(A_1\times\cdots\times A_{n-1}\)是可数集，根据假定\(A_n\)是可数的，上段已经证明这样两个集合的积是可数集，所以\(A_1\times\cdots\times A_n\)也是可数的。
如果能论断可数集的可数积是可数的，那就太好了，可惜这个结论并不成立。
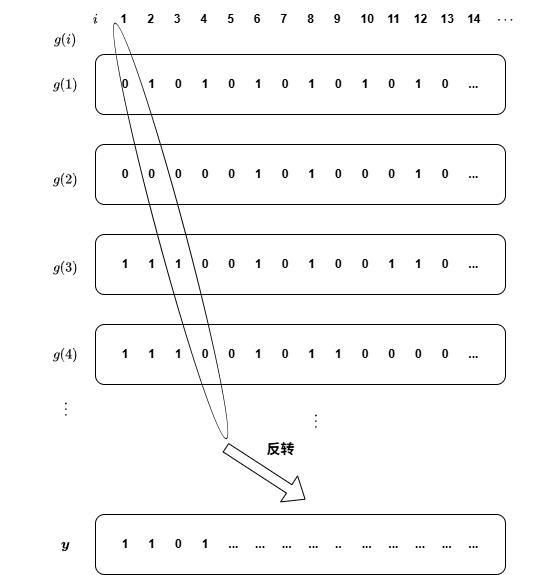
定理 7.7 设\(X\)表示二元素集\(\{0,1\}\)。那么集合\(X^{\omega}\)不可数。
证明 我们证明，任何函数
\[g:\mathbb{Z}\rightarrow X^{\omega} \]
都不是满射。为此，将\(g(n)\)表示成
\[g(n)=(x_{n1},x_{n2},x_{n3},\cdots,x_{nn},\cdots) \]
其中每一个\(x_{ij}\)为0或1。然后定义\(X_{\omega}\)的元素\(\bm{y}=(y_1,y_2,\cdots,y_n,\cdots)\)，使得
\[y_n=\begin{cases} 0,&x_{nn}=1,\\ 1,&x_{nn}=0. \end{cases} \]
（如果我们把数\(x_n\)排列成一个矩形方阵，那么其中元素\(x_{nn}\)总在这个方阵的对角线上，我们选取\(\bm{y}\)使其第\(n\)个坐标不同于对角线上的\(x_{nn}\)。）
于是，\(\bm{y}\)是\(X_{\omega}\)的一个元素，并且\(\bm{y}\)不在\(g\)的像中。对于给定的\(n\)，点\(g(n)\)与点\(\bm{y}\)至少有一个坐标（如第\(n\)个坐标）不相同。这证明\(g\)不是满射。
\\square
笛卡尔积\(\{0,1\}^{\omega}\)是不可数集的一个例子。下面的定理说明\(\mathcal{P}(\mathbb{Z}_+)\)是不可数集的另一个例子。
定理 7.8 设\(A\)是一个集合，那么不存在单射\(f:\mathcal{P}(A)\rightarrow A\)，也不存在满射\(g:A\rightarrow \mathcal{P}(A)\)。
证明 一般来说，若\(B\)非空，则单射\(f:B\rightarrow C\)的存在性蕴含着\(g:C\rightarrow B\)的存在性。我们可以对\(f\)像集中的每一个\(c\)定义\(g(c)=f^{-1}(c)\)，而对于\(C\)的其余点随意定义它在\(g\)下的像。
因此，我们只要证明对于任何一个给定的映射\(g:A\rightarrow\mathcal{P}(A)\)，\(g\)不是满射。对于任何一个点\(a\in A\)，\(a\)的像\(g(a)\)为\(A\)的子集，它可能包含\(a\)，也可能不包含\(a\)。令\(B\)为\(A\)中所有使\(g(a)\)不包含\(a\)的点\(a\)组成的子集，即
\[B=\{a|a\in A-g(a)\} \]
\(B\)可能为空集，也可能为整个\(A\)，这是没有关系的。可以认定\(B\)是\(A\)的一个子集，它不在\(g\)的像中。假定对于某个\(a_0\in A\)，\(B=g(a_0)\)。试问，\(a_0\)是不是一定属于\(B\)呢？根据\(B\)的定义，
\[a_0\in B\iff a_0\in A-g(a_0)\iff a_0\in A-B \]
在任何情况下都导致矛盾。
\\square
现在已经证明了不可数集的存在性。但是还没有提到我们最熟悉的一个不可数集------实数集。你可能以为\(\mathbb{R}\)的不可数性已经证明过了，如果假定任意实数可以用一个无限十进制数来表示的话（规定在表达式的最后不允许有无限个9，以避免\(0.\dot{9}=1\)这种两种表达式对应同一个数的情况。），那么改变以下定理 7.7证明中用过的对角线程序，就可以证明实数的不可数性。但是，这个证明在有些方面不十分完善，一个原因是实数的无限十进制表示并不是公理的简单推论，它需要费大力气去证明。另一个原因是实数的不可数性实际上并不依赖于\(\mathbb{R}\)无限十进制展开，也不依赖于\(\mathbb{R}\)的任何代数性质，它仅与\(\mathbb{R}\)的序性质有关。我们将在晚些时候（第27节）用\(\mathbb{R}\)的序性质来证明\(\mathbb{R}\)的不可数性。
需要指出的是，定理 7.7和定理 7.8的证明都使用了同一种方法------康托尔对角线法。读者可能会奇怪，定理 7.7的对角线方法比较明显，定理 7.8怎么就使用了对角线方法？事实上，我们将定理 7.8证明中集合\(A\)的元素对应定理 7.7证明中的下标\(1,2,\cdots\)，将\(A\)的子集对应无穷序列，将某元素是否在子集中分别对应无穷序列某分量的0和1。那么，定理 7.8证明中构造的子集\(B\)实际上就是定理 7.7证明中构造的\(\bm{y}\)。读者可以参考下面的示意图进行理解：
|-------------------------------------------------------------------------------------------------------------|-------------------------------------------------------------------------------------------------------------|
| 
定理 7.7证明 |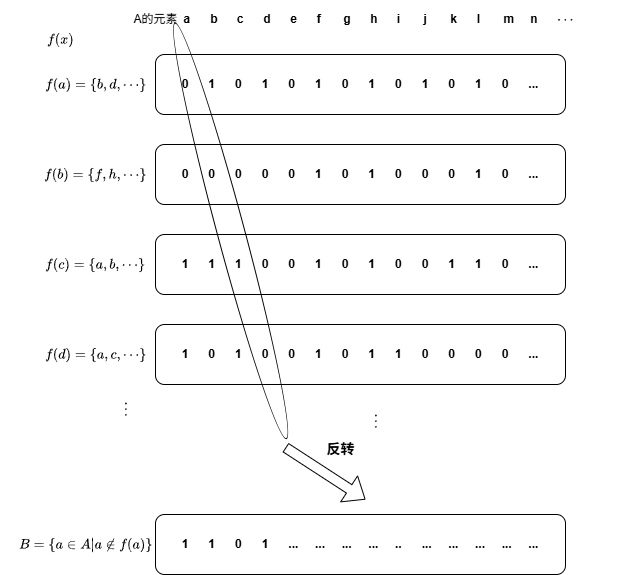 
定理 7.8证明 |
康托尔对角线法在集合论和数理逻辑、计算理论等诸多领域中都有应用。
观察推论 6.7与定理 7.1，我们会隐隐感觉到，似乎两个集合之间的单射和满射反映了两者之间的"大小关系"。事实上，数学将集合的大小抽象为基数 这个概念。对于有限集的情况，基数可以对应正整数或零，也可以定义相关的运算和大小关系。与之类比，我们设集合\(A\)的基数为\(\aleph_A\)，集合\(B\)的基数为\(\aleph_B\)。那么有
\[\begin{gathered} \aleph_A \leqslant \aleph_B\iff \text{存在单射}f:A\rightarrow B\\ \aleph_A \geqslant \aleph_B\iff \text{存在满射}f:A\rightarrow B\\ \aleph_A = \aleph_B\iff \text{存在一一对应}f:A\rightarrow B\\ \aleph_A+\aleph_B=A\times\{0\}\cup B\times\{1\}\text{的基数}\\ \aleph_A\times \aleph_B=A\times B\text{的基数}\\ {\aleph_B}^{\aleph_A}= [B^A=\{f|f:A\rightarrow B\}]\text{的基数} \end{gathered} \]
这些基数运算或关系的性质与非负整数的运算和关系性质基本一致。借助此，我们可以方便地证明某些集合的基数。例如，设\(\mathbb{Z}+\)的基数为\(\aleph_0\)，那么\(A=\{f|f:\{0,1\}\rightarrow \mathbb{Z}+\}\)的基数为\({\aleph_0}^2=\aleph_0\times \aleph_0=\aleph_0\)（最后一个等号成立的原因参考推论 7.4）。又对于\(D=\{f|f:\mathbb{Z}+\rightarrow\mathbb{Z}+\}\)，\(E=\{f|f:\mathbb{Z}_+\rightarrow\{0,1\}\}\)。前者基数为\({\aleph_0}^{\aleph_0}\)，后者基数为\(2^{\aleph_0}\)。由\(2<\aleph_0\)可知\(2^{\aleph_0}\leqslant{\aleph_0}^{\aleph_0}\)。又\(2^{\aleph_0}=2^{\aleph_0\times\aleph_0} = (2^{\aleph_0})^{\aleph_0} \geqslant {\aleph_0}^{\aleph_0}\)（最后的不等式成立的原因参考定理 7.7）。故\(2^{\aleph_0}={\aleph_0}^{\aleph_0}\)，集合\(D\)和\(E\)具有相同的基数。
需要指出的是，定理 7.8中\(\mathcal{P}(A)\)的基数显然严格大于\(A\)的基数（存在单射\(f:A\rightarrow \mathcal{P}(A),f(a)=\{a\}\)，但不存在满射\(g:A \rightarrow \mathcal{P}(A)\)）。这说明没有最大的基数。如果有，只需取对应集合的幂集即可获得更大的基数，矛盾。