文化水平:初二
文章只介绍反比例函数的深层理解、题目技巧与应用。文章需要掌握的前置知识:
对\(k\)的理解
众所周知,反比例函数有且只有一个参数\(k\),这导致它相对于一次函数来说变数更小。那么,让我们深入理解\(k\)的意义。
在函数\(y=\frac k x\)中,\(k\)又被称为比例系数。它的绝对值在几何上,经常被阐述为:从反比例函数图像上引出的两条垂直于横纵坐标轴的线段与坐标轴所围成的矩形的面积 。嗯?很懵?看不懂?那就用"形"的方法直观理解一下吧。
主播也是用上几何画板了好吧awa
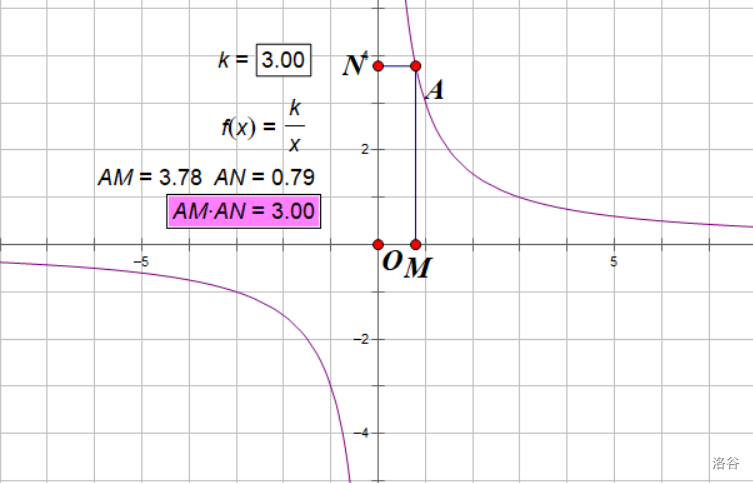
在计算机绘图软件中,新建参数\(k\)并新建函数\(y=\frac k x\)。在函数图像上任取一点\(A\),作\(AM⊥x, AN⊥y\)。然后度量\(AM\)、\(AN\)的坐标距离,并计算\(AM\cdot AN\)(即\(S_{矩形AMON}\))。拖拽点\(A\),观察\(AM\cdot AN\)的变化情况。右击参数\(k\),选择"生成参数的动画",观察\(AM\cdot AN\)随\(k\)的变化情况。
可以看出,\(AM\cdot AN≡|k|\),且不随\(A\)点位置变化而变化。因此,我们说,\(|k|\)表示从反比例函数图像上引出的两条垂直于横纵坐标轴的线段与坐标轴所围成的矩形的面积。
接下来,用"数"的方法证明一下吧。
已知反比例函数\(y=\frac k x\)可变形为\(xy=k\)。在平面直角坐标系中,\(x\)、\(y\)的几何含义是坐标系中任意一点的横坐标(\(x\))和纵坐标(\(y\)) 。又已知坐标系中任意一点向\(x\)轴作垂线段长为其纵坐标的绝对值,向\(y\)轴作垂线段长为其横坐标的绝对值 ,因此有:
反比例函数图像上任意一点横纵坐标的乘积等于\(k\)。
命题得证。
也正是这个原因,反比例函数的题目通常和坐标系中求面积结合起来考查。
待定系数法确定反比例函数
已知反比例函数只有一个参数,因此在使用待定系数法求解时只需要\(1\)个方程即可。这是基本操作。
例题:已知反比例函数图像过\(A(-2, -3)\),求反比例函数表达式。
\[解:设y=\frac k x(k为常数,k\neq 0),则有: \]
\[\frac k {-2} = -3 \]
\[k = 6 \]
\[\therefore 反比例函数表达式为y=\frac 6 x。 \]
反比例函数与一次函数
在上一章中我们已经证明了反比例函数\(y=\frac k x\)与正比例函数\(y=x\)的交点为\((±\sqrt k, ±\sqrt k)\),显然它们关于原点对称。那么,能否证明\(y=\frac a x\)和\(y=bx\)的交点也关于原点对称呢?
\[解:设交点坐标为P(m,n),则有: \]
\[\left\{ \begin{aligned} &mn=a&(1)\\ &bm=n&(2)\\ \end{aligned} \right. \]
\[(2)式代入(1)式,得: \]
\[bm^2=a, m=±\sqrt \frac a b \]
\[代入(1)式,得: \]
\[n=±\frac a m=±\frac a {\sqrt \frac a b}=±\sqrt {a^2 \cdot \frac b a}=±\sqrt {ab} \]
\[\therefore P点坐标为(±\sqrt \frac a b, ±\sqrt {ab}),显然它们关于原点对称。 \]
命题得证。
于是,我们得到如下真命题:
反比例函数\(y=\frac {k_1} x\)与正比例函数\(y=k_2x\)(\(k_1\)、\(k_2\)同号)有两个交点,这两个交点关于原点对称。
其实,题目中很多时候会将反比例函数与一次函数结合起来,用图像进行考察。请看下题:
13.一次函数\(y=kx\)与反比例函数\(y=-\frac 4 x\)的图像相交于\(A、B\)两点,点\(A\)的坐标为\((a,2)\)。
\((1)\)求\(a\)、\(k\)的值。
\((2)\)将直线\(y=kx\)向上平移\(m\)(\(m>0\))个单位长度,与双曲线\(y=-\frac 4 x\)在第二象限的一支交于点\(C\),与\(x\)轴交于点\(E\),与\(y\)轴交于点\(P\)。若\(PE=PC\),求\(m\)的值。
整体思路:
\((1)\)题先代入反比例函数解出\(a\),然后用一次函数待定系数法解出\(k\)。
\((2)\)题稍难,需要用\(m\)表示\(C\)点的坐标。向上平移\(m\)个单位长度,因此平移后得\(y=-x+m\)。把\(P\)、\(E\)的坐标用\(m\)算出来,然后用平行---中点---"\(8\)"字全等 表示\(C\)点坐标再代入反比例函数可以解出\(m\)。
答案:

反比例函数的动点问题
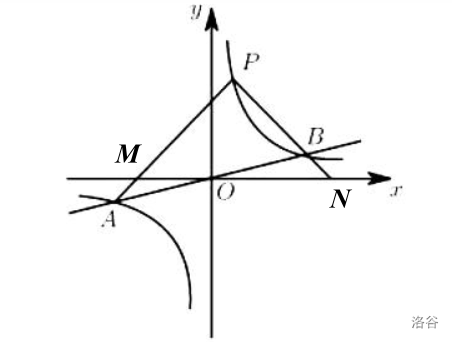
如图,反比例函数\(y=\frac k x\)的图像与一次函数\(y=\frac 1 4 x\)的图像交于点\(A\)、\(B\),点\(B\)的横坐标是\(4\)。点\(P\)是第一象限内反比例函数图像上的动点,且在直线\(AB\)的上方。
\((1)\)若点\(P\)的坐标是\((1,4)\),直接写出\(k\)的值和\(\triangle PAB\)的面积。
\((2)\)设直线\(PA\)、\(PB\)与\(x\)轴分别交于点\(M\)、\(N\),求证:\(\triangle PMN\)是等腰三角形 。
我们先进行一些前置操作。
\(y_B=\frac 1 4 x_B=1\),\(B(1,4)\)。
\(k=x_B\cdot y_B=1\times 4=4\)。
计算一下交点\(A: \left\{ \begin{aligned} &y_A=\frac 4 {x_A} \\ &y_A=\frac 1 4 x_A\\ \end{aligned} \right. \)可解得\(A(-4, -1)\)。
第一题很简单,\(k=4\);
\(S_{\triangle PAB}\)可用割补法得到结果\(15\)。
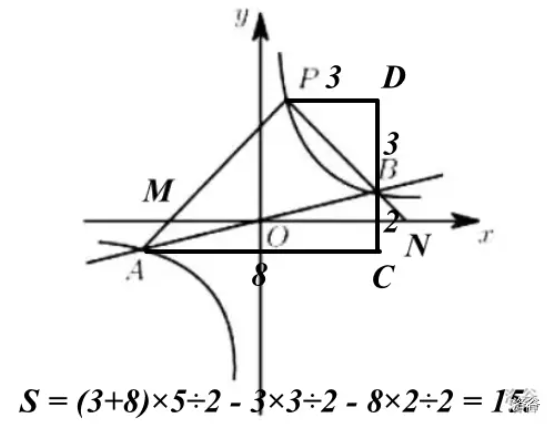
第二题的话,我们需要理清一下思路。
对于坐标系内证明等腰三角形 的"流派"主要有以下\(2\)个:
- 证明\(PM=PN\)(通过距离公式实现)。
- 过\(P\)向\(x\)轴引一条垂线\(PH\),只需证明\(MH=NH\)即可,后续需要完善一下。
那么,在这题我们选择哪种方法呢?其实,两种都可以 。
不管使用哪种方法,\(P(1,4)\)是没法再用了,我们便只能设\(P(t, \frac 4 t)\)(请出祖传设\(t\)技能),明确\(0<t<4\)。这个\(4\)是因为题目规定\(P\)在\(AB\)上方,即在\(B\)点左侧。
表示出\(PM\)和\(PN\)的表达式,有\(PM: y=\frac 1 tx-\frac {t-4} t\);\(PN: y=-\frac 1 tx+\frac {t+4} t\)。它们与\(x\)轴的交点分别为\(M(t-4, 0)\)、\(N(t+4, 0)\)。
这样,选哪种方法都不为过了。考虑方法\(1\):\(PM=\sqrt {(\frac k t)^2+4^2}\),\(PN=\sqrt {(\frac k t)^2+4^2}\),无需多证,\(PM=PN\)。再考虑方法\(2\),那就更为简单:\(MH=NH=4\),直接由\(PH垂直平分MN\)证\(PM=PN\)。
反比例函数大题总结
现在,你知道这类函数大题一般如何考察了吗?
一般地,函数大题具有以下特征:
- 结合反比例函数和一次函数(正比例函数)。
- 在函数表达式中设出多个参数。
- 分多个小问。
- \((1)\)题一般要求通过已知条件解出参数。
- \((2)\)题一般在坐标系中证明或添加条件求解,通常需要数形结合。
- \((3)\)题更为进阶,可能需要探究新函数的图像和性质,以及更为复杂的数形结合问题。
现在,我们就可以轻松地应对中等或更难的函数大题了。
反比例函数的解析问题
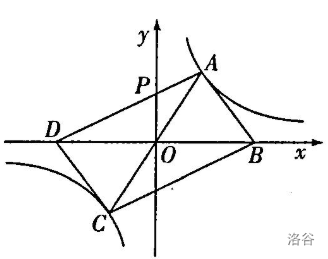
(株洲)平行四边形\(ABCD\)的两个顶点\(A\)、\(C\)在反比例函数\(y=\frac k x\)的图像上,点\(B\)、\(D\)在\(x\)轴上,且\(B\)、\(D\)两点关于原点对称,\(AD\)交\(y\)轴于点\(P\)。
\((1)\)已知点\(A\)的坐标为\((2,3)\),求\(k\)的值及\(C\)点的坐标。
\((2)\)在\((1)\)的条件下,若\(S_{\triangle APO}=2\),求点\(D\)到直线\(AC\)的距离。
怎么样?有没有一种"坐标系几乎退出舞台"的感觉?
这种具有频繁或强烈的数形结合、需要几何与代数知识几乎\(1:1\)运用的题目,我们称之为解析问题。
做解析问题其实不需要太慌张,让我们先按部就班把第\((1)\)题做完。
\(k=x_A\cdot y_A=2\times 3=6\)。已知\(▱ABCD\),则\(A\)、\(C\)关于\(O\)成中心对称,易知\(C(-2, -3)\)。
\((2)\)题就有点麻烦了。要求点\(D\)到直线\(AC\)的距离,有两种主流方法。
- 结合面积法,将其转换为几何问题。
- 通过"平行线之间距离处处相等"进行转换。
- 爆肝\(DH\)解析式,然后用距离公式。
显然,第一种更为简单,因为本题已经出现了面积。
首先,因为\(A(2,3)\),我们可以根据\(S_{\triangle APO}=OP\cdot x_A\times \frac 1 2=OP=2\)求得\(OP=2\)。
接下来,既然用面积法解题,我们就要把\(DH\)放到\(\triangle OCD\)中解。那么,应该用另一种方法求出\(S_{\triangle OCD}\),显然我们选择\(OD\cdot |y_C|\times \frac 1 2\)。\(OD\)可以选择求出\(AP: y=\frac 1 2x+2\),然后计算交点即为\(D(-4,0)\)。\(S_{\triangle OCD}=4\cdot |-3|\times \frac 1 2=6\)。
\(OC\)可用勾股定理推出\(\sqrt {2^2+3^2}=\sqrt {13}\),即得\(DH\cdot OC\times \frac 1 2=6\),代入并解得\(DH=\frac {12} {\sqrt {13}}=\frac {12}{13}\sqrt {13}\)。
即:\(D\)到直线\(AC\)的距离为\(\frac {12}{13}\sqrt {13}\)。
在做解析问题时,需要时刻牢记数形结合 。就像此题,如果你只记得代数,爆肝\(DH\)解析式然后用距离公式进行计算,不仅会超纲,计算量还很大。如果可以用面积法秒解的话,就可以节省计算量。但是,如果你只记得几何,那么\(OD\)的长度就想不到用表达式法代入,这是大忌。因为,如果不用表达式法,你能且只能用相似三角形,而这在初二是超纲的。
因此,数形结合是解析问题的致胜法宝。这样,它与普通的函数题便别无两样。
反比例函数的拓展问题
学一次函数的时候,老师告诉你:
一次函数的\(k\)值如果变化,函数图像会绕某一定点转转 。
一次函数的\(b\)值如果变化,函数图像会沿上下方向移移 。(具体平移\(\Delta b\)个单位。)
那么, 学了反比例函数的你,有没有想过:
反比例函数为什么没有"转转"和"移移"呢?
哈哈,不是没有,而是你还没学。这就来了。
研究函数\(y=\frac 6 {x+2}+3\)。
(学生\(OS\))啊不是,这是什么函数?四不像?
没事,我们先画出它的图像看看。
(列表描点过程略。)
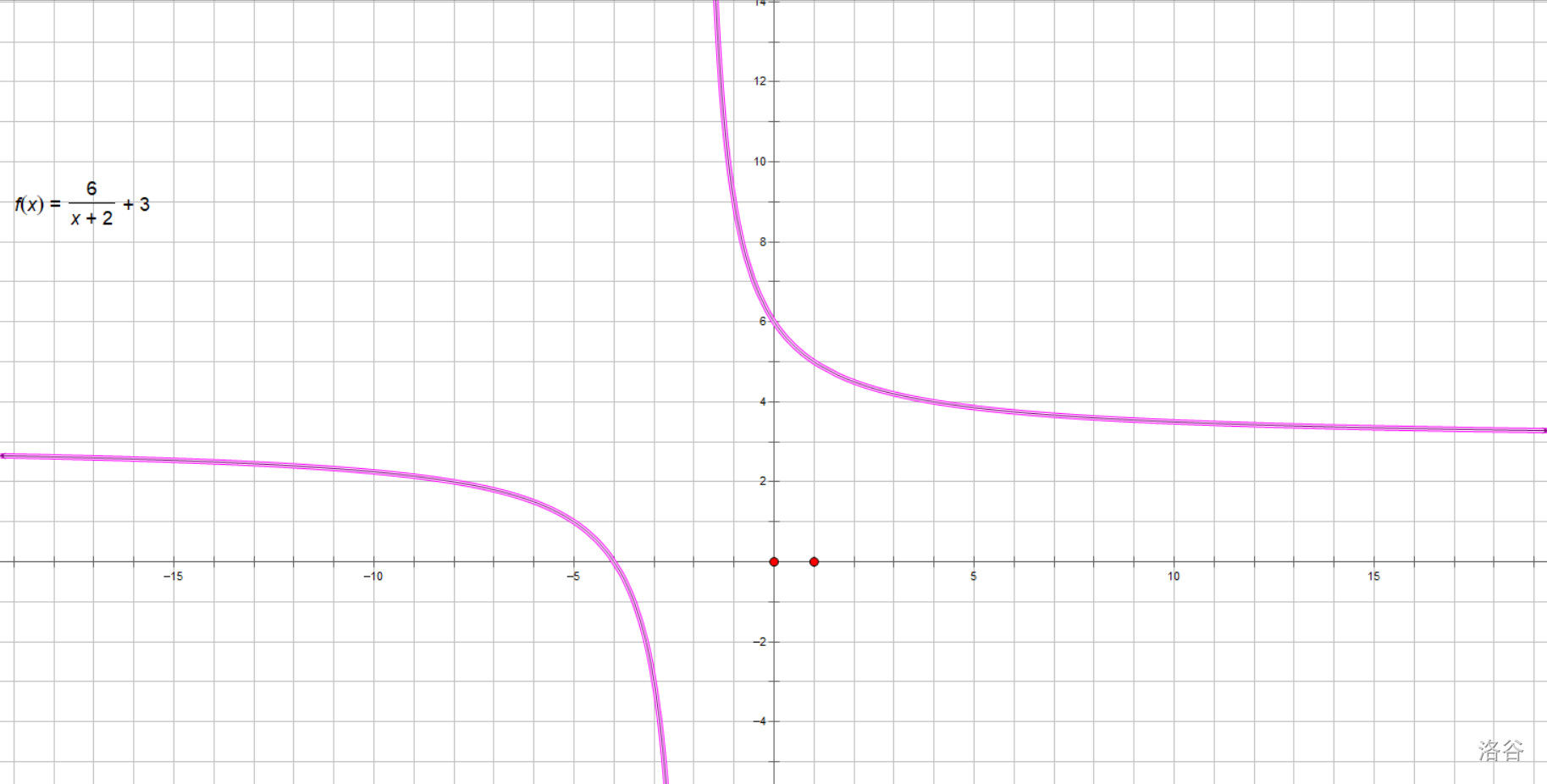
看!像不像反比例函数!
但是,它好像相比于反比例函数看来,有了一定变换,看着像是平移变换。
等下!根据一次函数万能平移解析式变换口诀 ("左加右减,上加下减"),那反比例函数是否也适用呢?
事实上,只要是个函数,它都适用。
根据我们的口诀,我们发现,这个函数就是在反比例函数\(y=\frac 6 x\)的基础上,向左平移\(2\)个单位 ,然后向上平移\(3\)个单位。再一看图像,还真是!
这下,它的所有性质应该都继承了反比例函数\(y=\frac 6 x\)。其实,只不过是所谓的"临界线"变成了直线\(x=-2\)和直线\(y=3\)。
增减性:当\(x>-2\)和\(x<-2\)时,都有\(y\)随\(x\)的增大而减小。
对称性:关于\((-2,3)\)对称,关于直线\(y=x+5\)和\(y=-x+5\)对称。
最值:\(x∈(-∞, -2)\&(-2, +∞), y∈(-∞, 3)\&(3, +∞)\)。
另外有几点需要你掌握:
- 函数\(y=\frac k {x+a}+b\)的图像与\(x\)、\(y\)两轴最多各有\(1\)个交点 。当\(a=0\)时,图像与\(y\)轴无交点;当\(b=0\)时,图像与\(x\)轴无交点。
- 函数\(y=\frac k {x+a}+b\)的图像随\(k\)的变化情况与反比例函数的基本一致。
那么,考试可能会考察哪些类型的题目呢?下面,我们暂且将函数\(y=\frac k {x+a}+b(k, a, b为常数,k\neq 0)\)称为反比例拓展函数。
反比例拓展函数与一次函数的交点
给一道我们苏科版数学《学习与评价》单元练习的一道题目。

看似都是让我们探索所谓的"奇点",其实是考察这类反比例拓展函数的。因为,第\((2)\)题的第I. 小问的答案是这样的:
\[由题意得对于奇点坐标(x, y),xy=2x+2y \]
\[整理得y=\frac {2x} {x-2} (学生OS:这算什么函数?) \]
\["分离常数",得y=\frac 4 {x-2}+2 \]
哦哦哦!是反比例拓展函数啊!
那么, 我们就可以用反比例拓展函数的结论了。来!解II. \\(小问! !\[\](https://cdn.luogu.com.cn/upload/image_hosting/8wa6t856.png) \\)①\\(图像与坐标轴没有交点,正确。\\)a\\(、\\)b都不为\(0\),因此与\(x\)、\(y\)轴各有\(1\)个交点。但是由于原题中\(x\)有取值范围为\(x>2\),所以这一支与坐标轴没有交点。
\(②\)在第一象限内\(y\)随\(x\)的增大而减小。正确。容易看出,在第一象限 ,只有一支图像经过,而满足增减性要求。
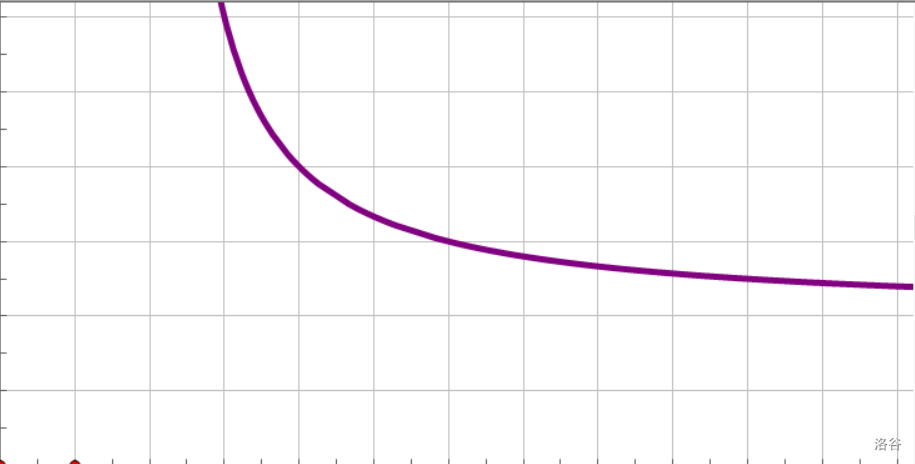
\(③\)对于图像上任意一点\((x, y)\),\((x-2)(y-2)\)为定值。正确。已知\(y=\frac 4 {x-2}+2\),有\(y-2=\frac 4 {x-2}\),因此\(x-2\)与\(y-2\)成反比例。
那么,第\((3)\)小题呢?
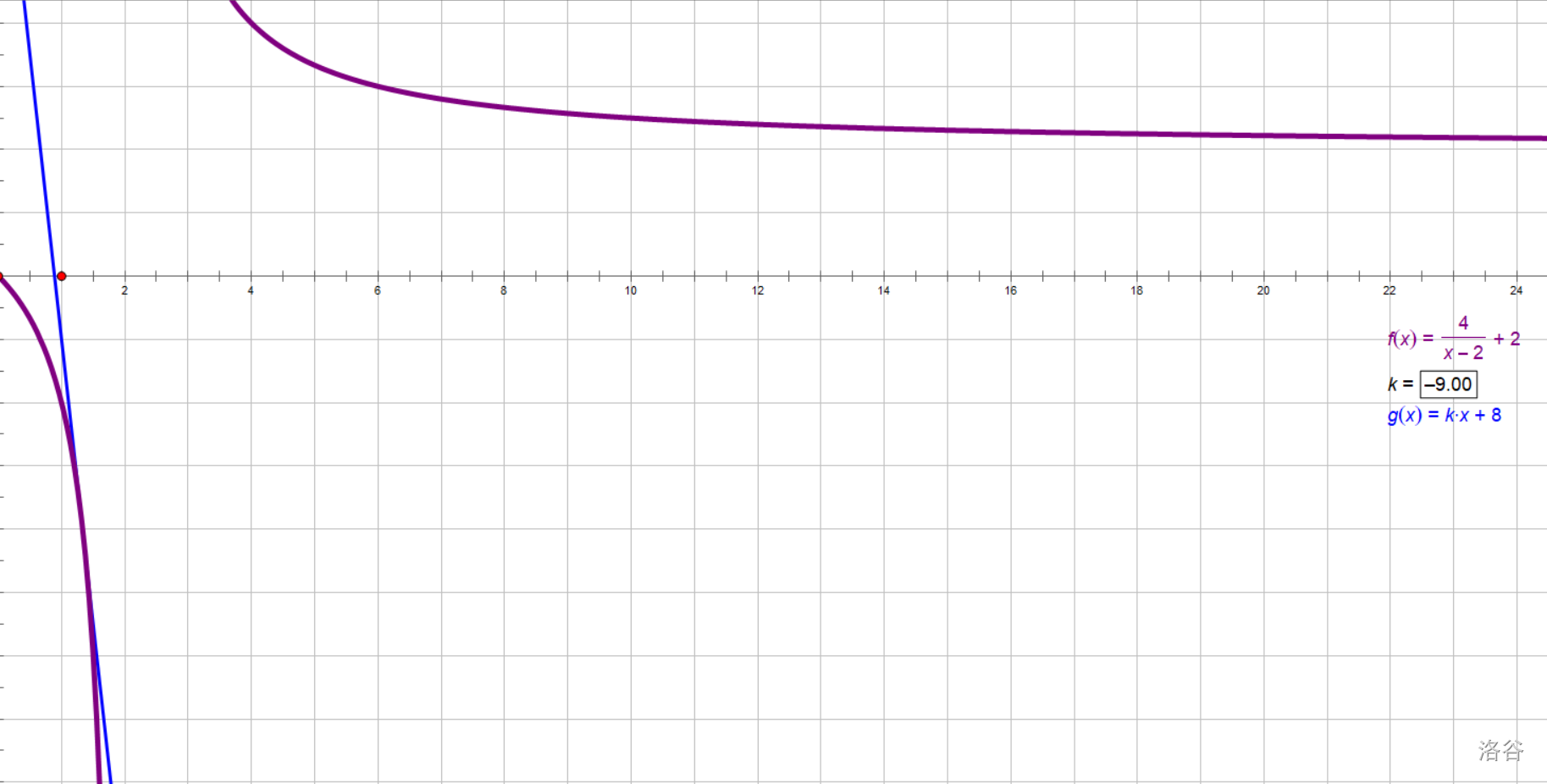
在第一象限内,一次函数\(y=kx+8\)的图像上奇点的个数随\(k\)值的变化而变化,直接写出奇点的个数及对应的\(k\)的取值范围。
这就是题型\(A\):反比例拓展函数与一次函数的交点。这题还是比较难的,带上了一次函数的"转转"变换。
解出这类题目的关键是画图。那么,让我们加上函数\(y=kx+8\),看一看函数转动时,交点的个数有什么关系吧。
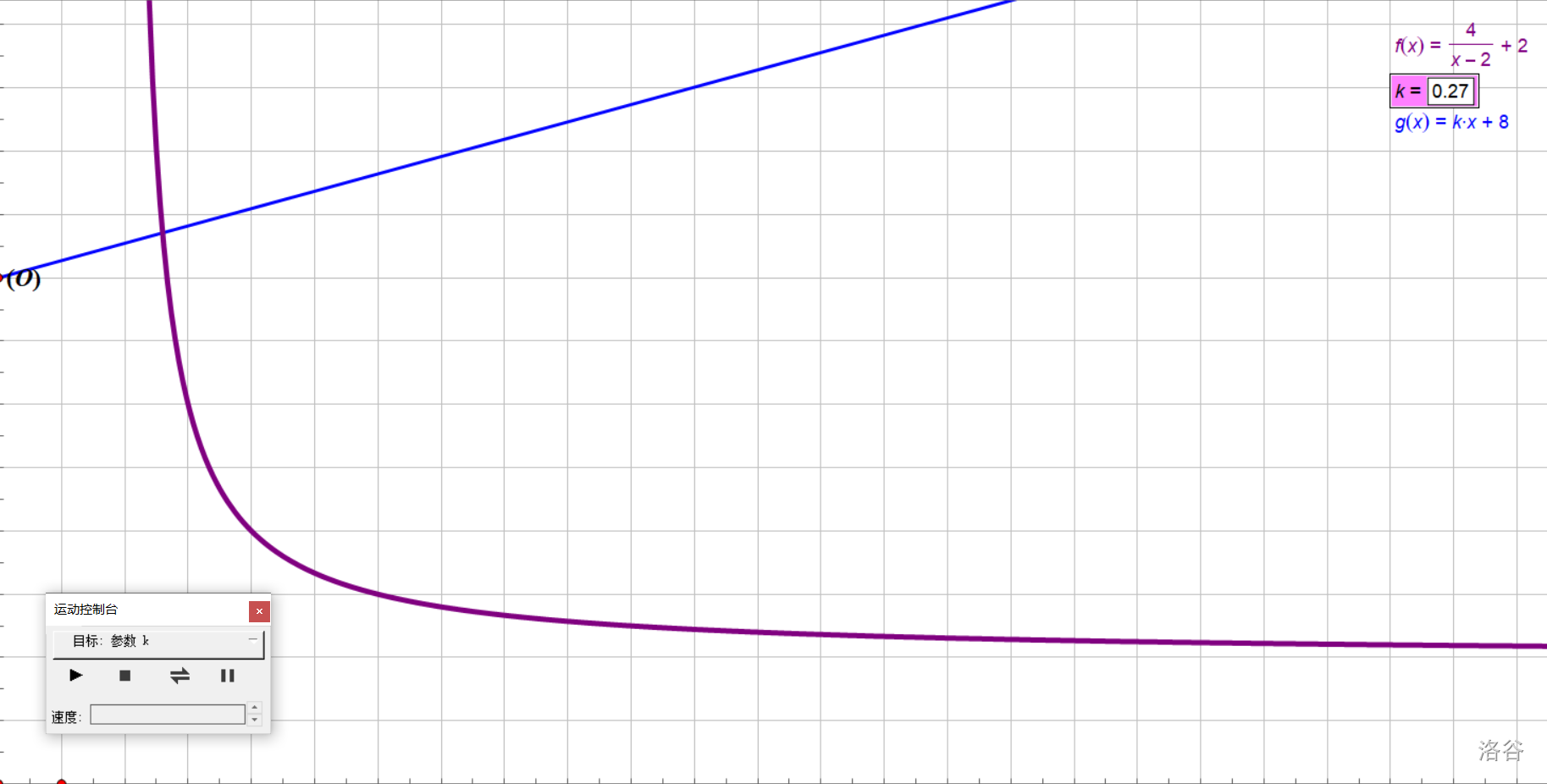
先研究\(k>0\)时的情况。可以发现,当\(k∈\{0<k<∞\}\)时,直线与反比例拓展函数永远有且只有一个交点。当\(k\)很大时,两者在很远的地方也会有一个交点。
当\(k<0\)时,又会分一些情况。首先,当\(k\)刚刚比\(0\)小一点 时,会发现它与拓展函数有两个交点。但是,好像在某一个分界处,两图像相切,只有一个交点。再往下就没有交点了。
这个特殊点就是\(k=-1\)时。
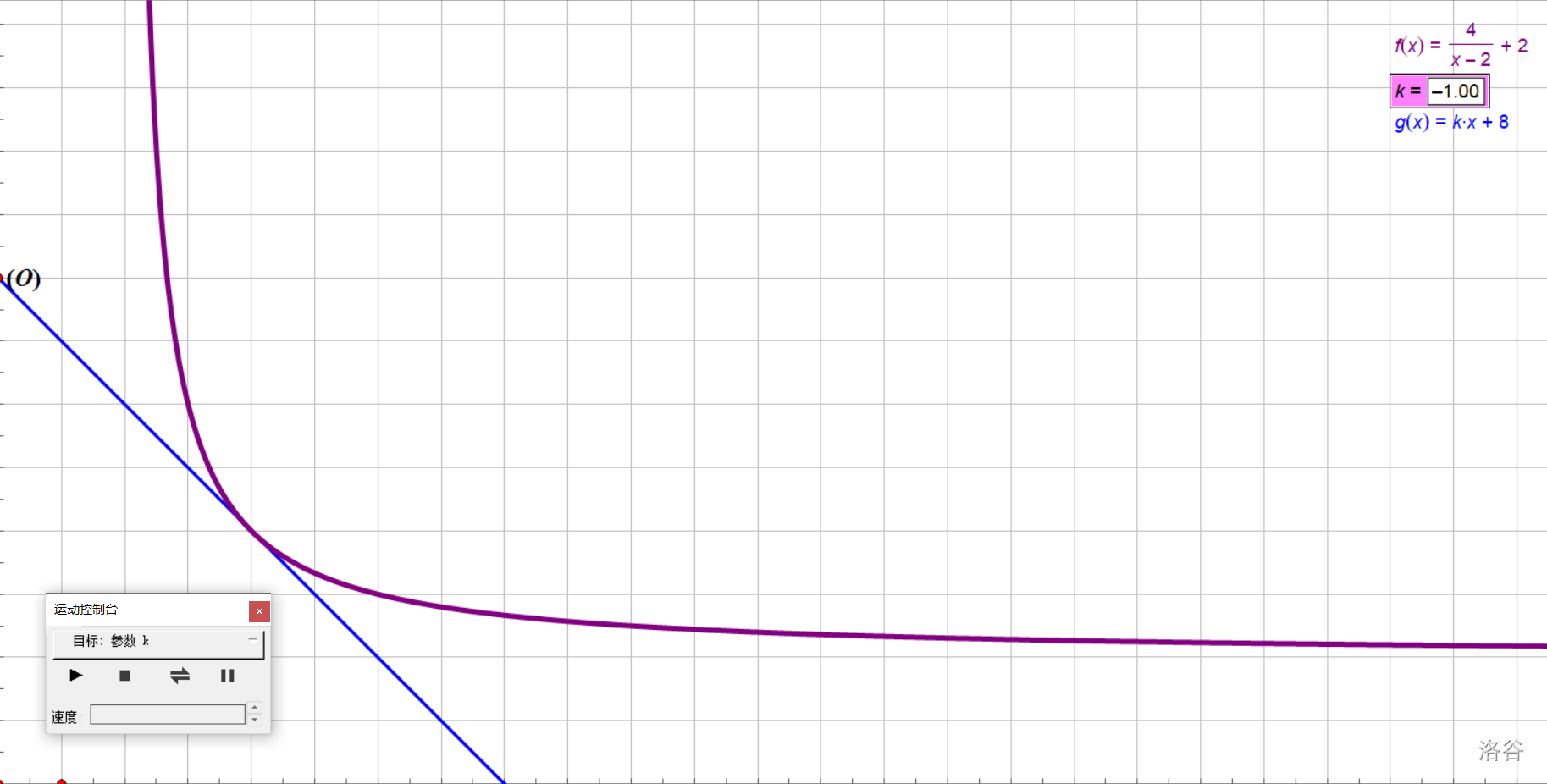
你问我是怎么知道的?首先,这题是直接写出答案,你完全可以画图然后感受出来。
那如果非要证明的话,就要用到一元二次方程了,这里简述证明过程。
已知两函数交点的横坐标是方程组\(\left\{ \begin{aligned} &y=kx+8\\ &y=\frac 4 {x-2}+2\\ \end{aligned} \right.\)的解。
联立两方程组右侧,得\(kx+8=\frac 4 {x-2}+2\)。
等式两边同时乘\(x-2\),由于\(x\neq 2\),因此一些增根的情况不用考虑。\((kx+6)(x-2)=4\)。
展开并整理,得\(kx^2+(6-2k)x-16=0\)。
这是一个一元二次方程,若其有\(1\)个解,则相应的,直线与拓展函数将有且只有\(1\)个交点。而一元二次方程只有\(1\)个解的条件就是\(\Delta =b^2-4ac=0\)。
代入,\((6-2k)^2+64k=0\);展开,\(4k^2+40k+36=0\),还是一个一元二次方程。
套入求根公式,\(k=\frac {-40±\sqrt {40^2-4\times 4\times 36}} {2\times 4}\),\(k_1=-1\),\(k_2=-9(舍)\)。
你猜,那个\(-9\)是怎么来的?
原来交点跑到第四象限了呀,怪不得要舍掉呢。
综上,交点个数与\(k\)取值范围之间的关系为:
| 交点个数 | \(k\)的取值范围 |
|---|---|
| 0 | \(k<-1\) |
| 1 | \(k=-1\)或\(k>0\) |
| 2 | \(-1<k<0\) |
反比例拓展函数与方程
这个快速过一下。
解方程:\((x-3)^2=4\)(利用函数)。
这道题放在平时,想必大家都会做吧!那如果需要利用函数,而你又没学过二次函数,怎么办?
那就两边同时除以\(x-3\)吧。(但是,需要注意除以\(0\)的情况,因此检验:当\(x=3\)时,方程不成立,因此没有"失根"。)
\[\frac 4 {x-3}=x-3 \]
诶,又要利用函数,不就是要求\(y=\frac 4 {x-3}\)与\(y=x-3\)的交点吗?问题转化,下面不再赘述。
答案:\(x_1=5\),\(x_2=1\)。
反比例拓展函数与绝对值
【联合体期末】对函数图像\(y=|\frac 6 {x+1}-3|\)的性质进行研究。
按照我们的惯例,根本不需要它给小题,我们自己研究!
首先画出\(y=\frac 6 {x+1}-3\),基本操作了。
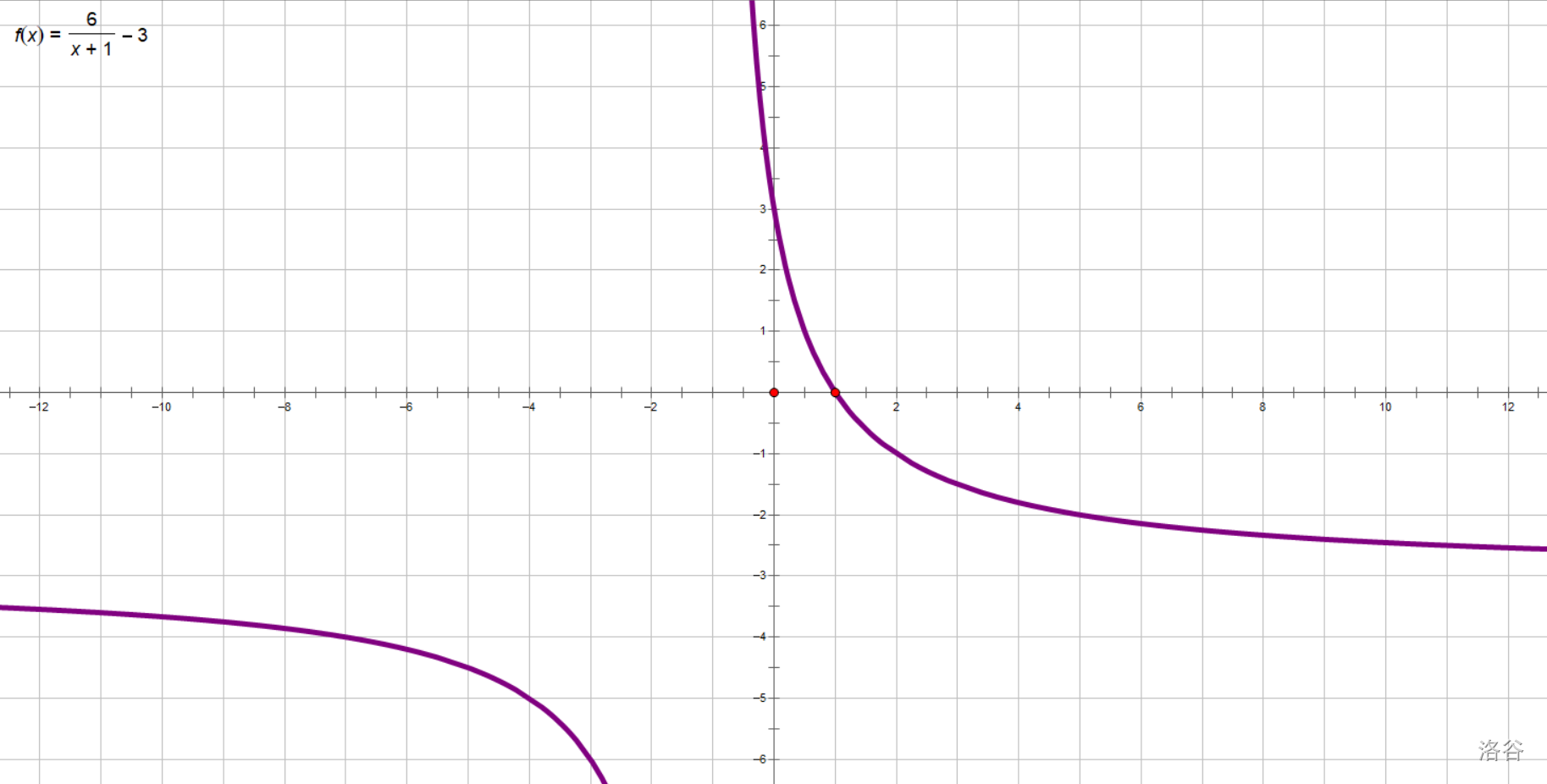
然后,根据研究一次函数与绝对值的经验,应该是三四象限部分图像翻过去 ,要求我们画草图并写出两条性质。
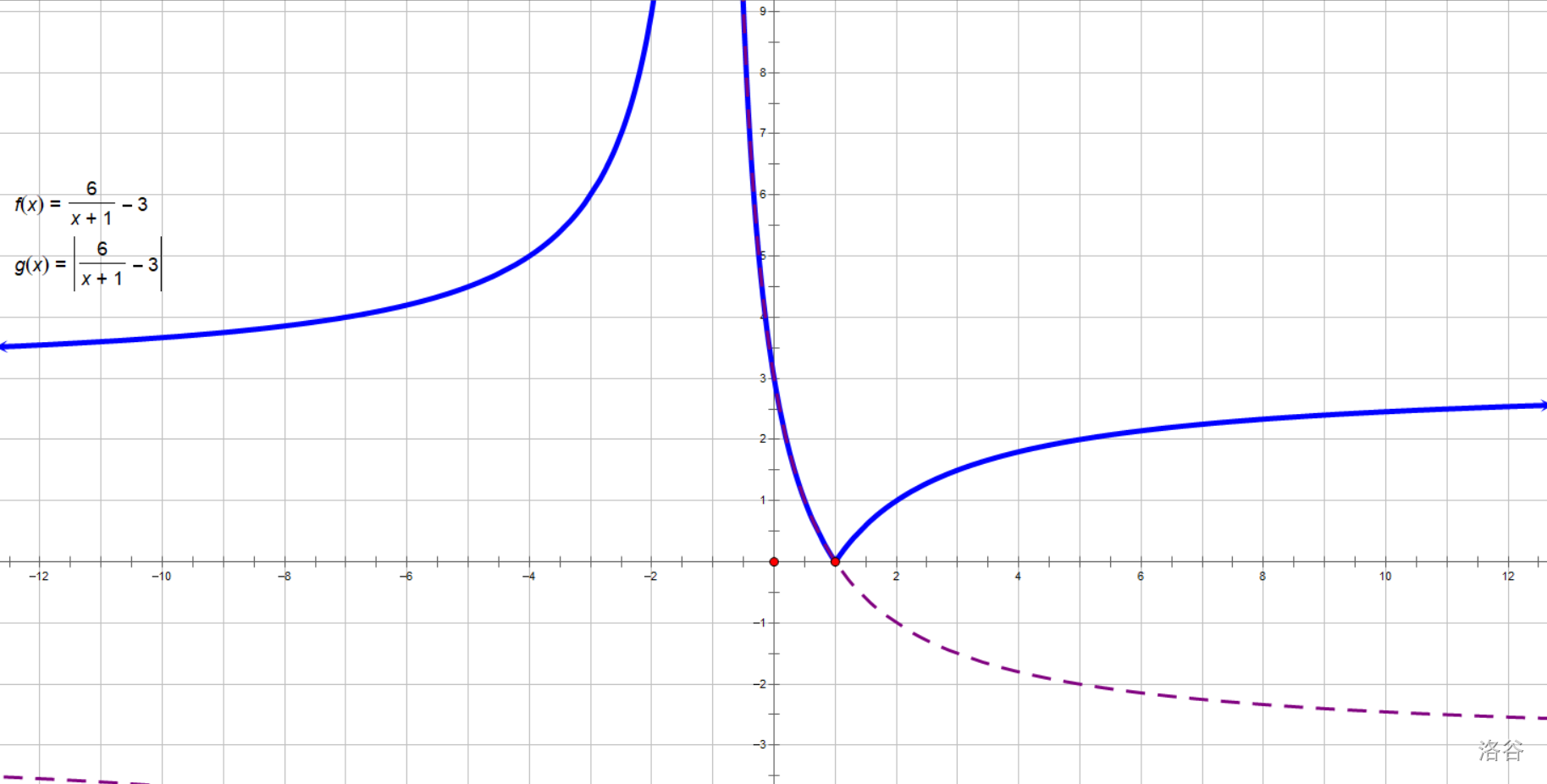
画出来呢,就是这个样子。
两条性质也很好写嘛,增减性和最值描述一遍。
\((4)\)研究后发现,方程\(|\frac 6 {x+1}-3|=a\)中,随着\(a\)的变化, 方程的解的个数也会有所变化。结合图像,就\(a\)的取值范围探讨方程解的情况。
嗯,这是一道很经典的反比例拓展函数、函数与绝对值、函数与方程的大题!!出题人很有水平!!
但是做起来不难。既然要\(|\frac 6 {x+1}-3|=a\),那就要\(y=a\),就是找\(y=a\)与\(y=|\frac 6 {x+1}-3|\)交点的个数与\(a\)取值范围之间的关系,拿着尺子水平推过去一顿分析就完事了。
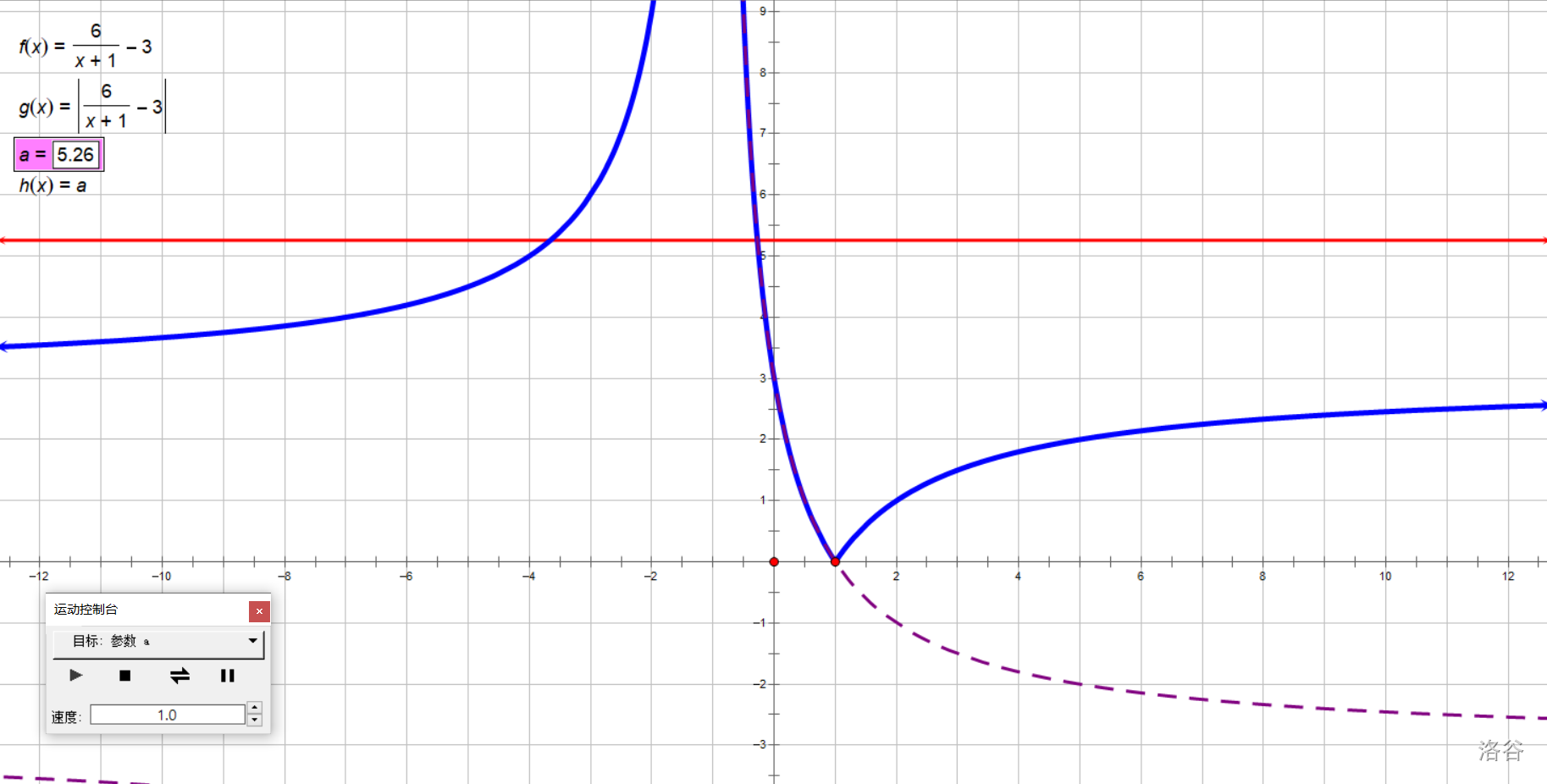
| \(a\)的取值范围 | 方程解 |
|---|---|
| \(a<0\) | 无解 |
| \(a=0\) | 有\(1\)个解(具体为\(x=1\)) |
| \(0<a<3\) | 有\(2\)个(正数)解 |
| \(a=3\) | 无解 |
| \(a>3\) | 有\(2\)个(负数)解 |
挑战中考
【\(2019\)鼓楼一模】把一个函数图像上每个点的纵坐标变为原来的倒数(原函数图像纵坐标为0的点除外)、横坐标不变,可以得到另一个函数的图像,我们称这个过程为倒数变换。
例如,将\(y=x\)的图像经过倒数变换后可得到\(y=\frac 1 x\)的图像。特别地,因为\(y=x\)图像上纵坐标为0的点是原点,所以该点不做变换,因此\(y=\frac 1 x\)的图像上也没有纵坐标为\(0\)的点。
\((1)\)请画出\(y=-x+1\)的图像和它经过倒数变换后的图像。
\((2)\)观察上述图像,结合学过的关于函数图像与性质的认识,
\(①\)猜想:倒数变换得到的图像和原函数的图像之间可能有怎样的联系?写出两个即可。
\(②\)说理:请简要解释你其中一个猜想。
第\((1)\)小题,直接秒的那种。
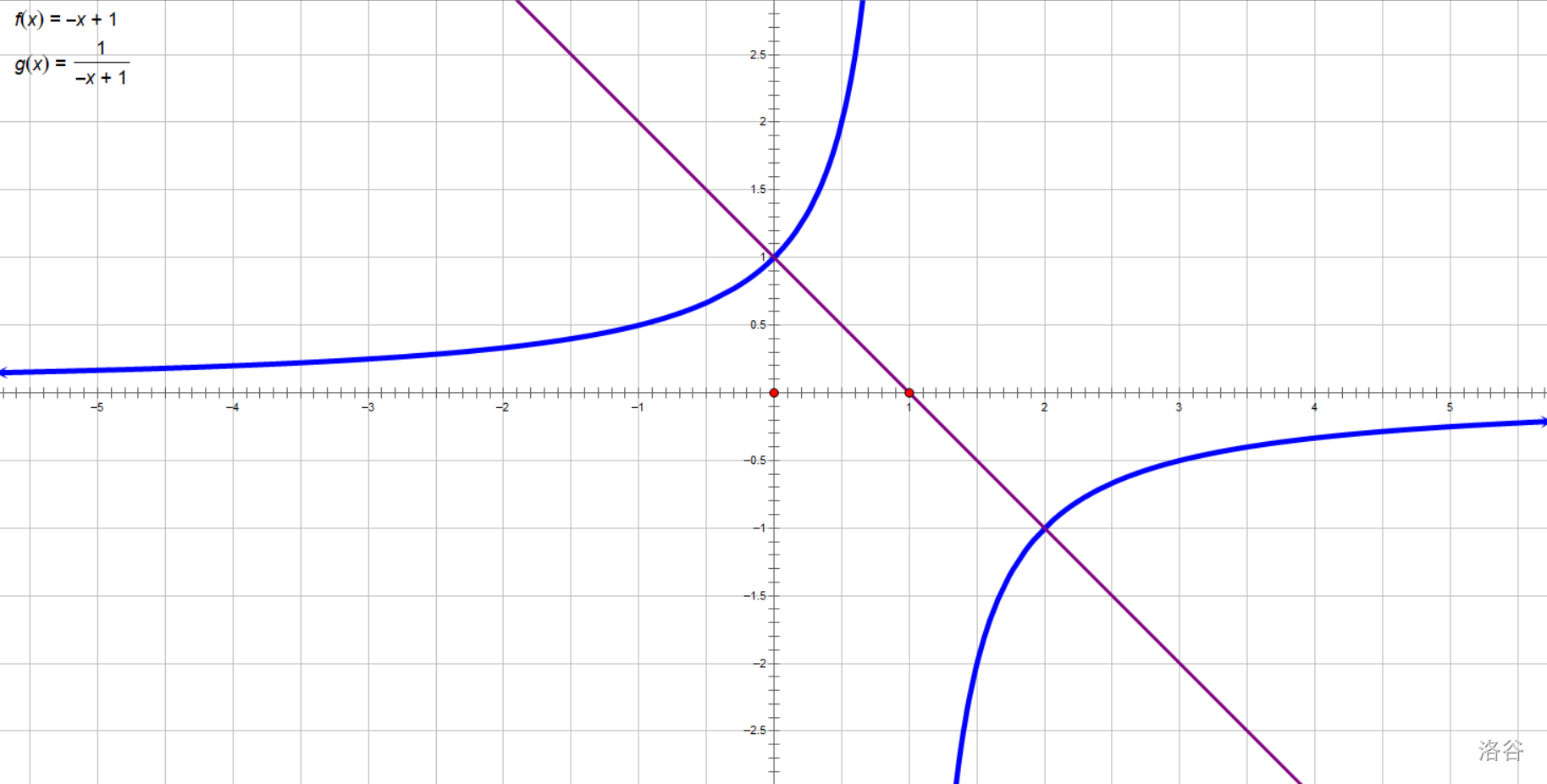
第\((2)\)小题需要我们写出两个性质。其中一个性质还是很好写的。
原图像\(x\)轴上方的部分,经倒数变换后仍在\(x\)轴上方;原图像\(x\)轴下方的部分,经倒数变换后仍在\(x\)轴下方。
那第二个该怎么写......
既然我们现在有了两个图像,那我们能研究的对象是不是又多了一个呢?
若两图像有交点,则交点的纵坐标应为\(1\)和\(-1\)。
这是我们观察\((1)\)小题的两个图像得出的结论。
既然猜想了,那我们进行论证。(以下是简要证明)
证明都很好想,需要围绕反比例函数进行证明。因为倒数就是和反比例函数挂钩的。
\[(1): \because进行了倒数变换, \]
\[\therefore 对于图像上一点(x,y),变换后为(x,\frac 1 y) \]
\[\because 令y'=\frac 1 y \]
\[\therefore 它们成反比例关系,二者同号。 \]
\[\therefore 它们保持相对于x轴位置不变。 \]
\[(2) 设倒数变换前y=f(x),则倒数变换后y'=\frac 1 {f(x)}。 \]
\[联立:\left\{ \begin{aligned} &y=f(x)\\ &y=\frac 1 {f(x)}\\ \end{aligned} \right.\]
\[解得f(x)=±1,即y=±1, \]
\[\therefore 交点的纵坐标为1或-1。 \]
没想到啊,中考题也被我们解出来了。
现在,你应该完全掌握了反比例函数的"移移"了吧。其实,反比例函数的"转转"由于过于复杂,考试永远也不会考。
反比例函数的应用
应用类的题目不是很难,我们简单过一下,找一个例题,讲明白所有应用。

这道学校讲义上的例题,不仅涵盖了分段函数,还有函数与不等式、函数与实际意义等等,算是应用类问题的天花板了。让我们解决一下这个问题。
第\((1)\)小题通常让我们计算表达式,这题也是如此,只不过分段函数更为难算。不妨一口气全设出来。
\[设y=\left\{ \begin{aligned} &k_1x+20&(0\leq x\leq b)\\ &100&(b< x\leq b+1)\\ &y=\frac {k_2} x&(b+1<x\leq c)\\\ \end{aligned} \right.\]
然后代入一些点:
\[k_2=x_D\cdot y_D=18\times 50=900 \]
\[令y=100, b+1=9, b=8(应检验) \]
\[8\times k_1+20=100, k_1=10 \]
由于说水温不能低于\(20\)度,故有\(y\geq 20\),可得\(x\leq 45\)(应检验并根据增减性说明)。
\[\therefore y=\left\{ \begin{aligned} &10x+20&(0\leq x\leq 8)\\ &100&(8< x\leq 9)\\ &y=\frac {900} x&(9<x\leq 45)\\\ \end{aligned} \right.\]
第\((2)\)题则是根据增减性与不等式联系解答,算是基本功。注意是从水烧开到泡茶。
令\(y=80\),则有\(\frac {900} x=80\),解得\(x=\frac {45} 4\),应检验。
\(\because k=900>0 \therefore\)当\(x>9\)时,\(y\)随\(x\)的增大而减小。
\(\therefore x\)最小为\(\frac {45} 4\),\(\frac {45} 4-8=\frac {13} 4\)。
因此,从水开到泡茶需要等待\(\frac {13} 4\)分钟。
此类题目基本都是利用模版答题,没有太大的难度。
至此,"反比例函数"系列内容已结束,之后若有值得考量的题目将会发表在新的帖子中。希望能够对你的反比例函数学习有帮助。