目录
1.程序功能描述
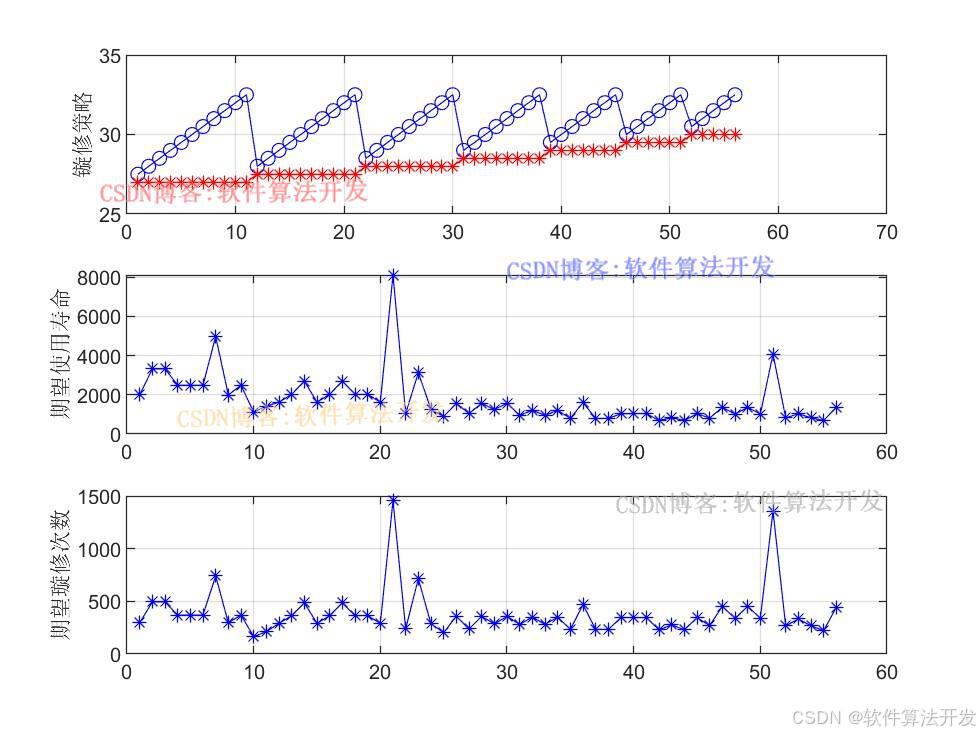
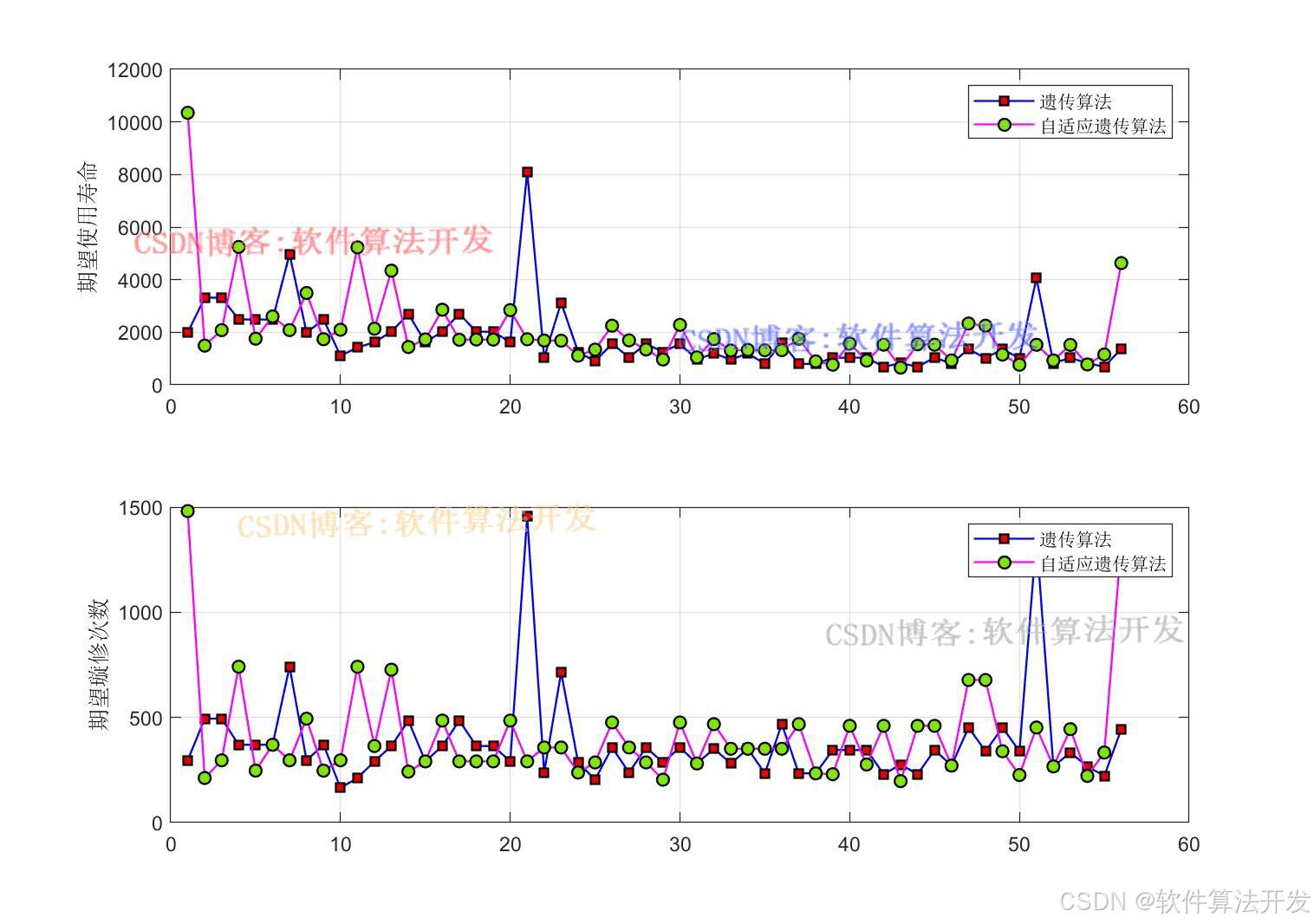
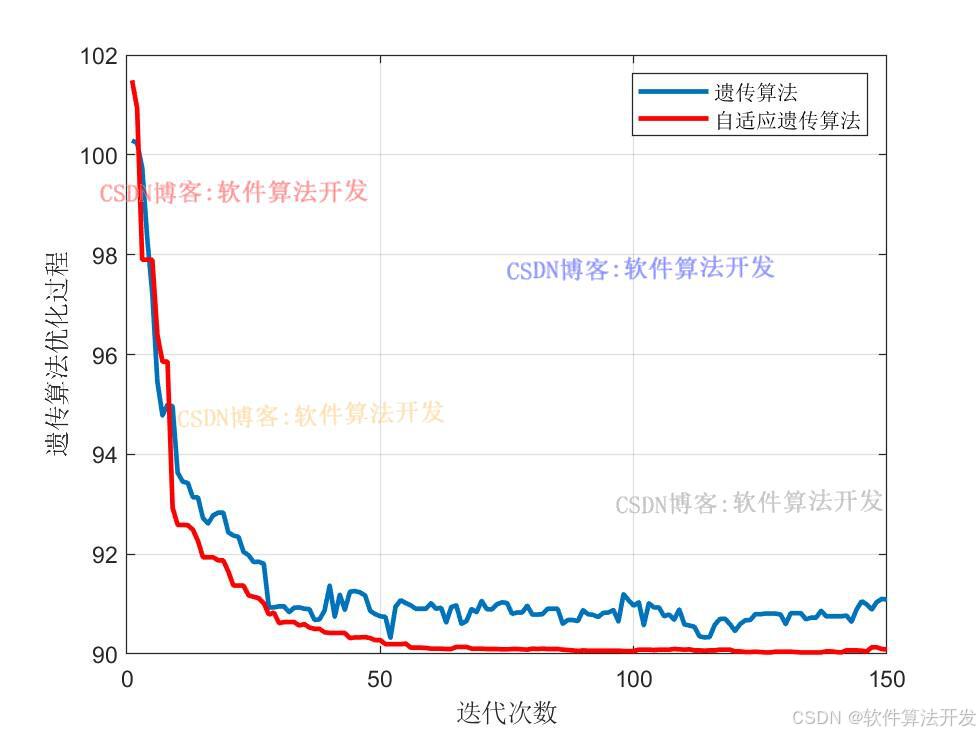
基于自适应交叉概率和变异概率遗传算法的地铁车辆使用寿命和璇修次数优化。对比传统的遗传优化算法和自适应交叉概率和变异概率遗传算法对地铁车辆使用寿命和璇修次数的优化结果。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行

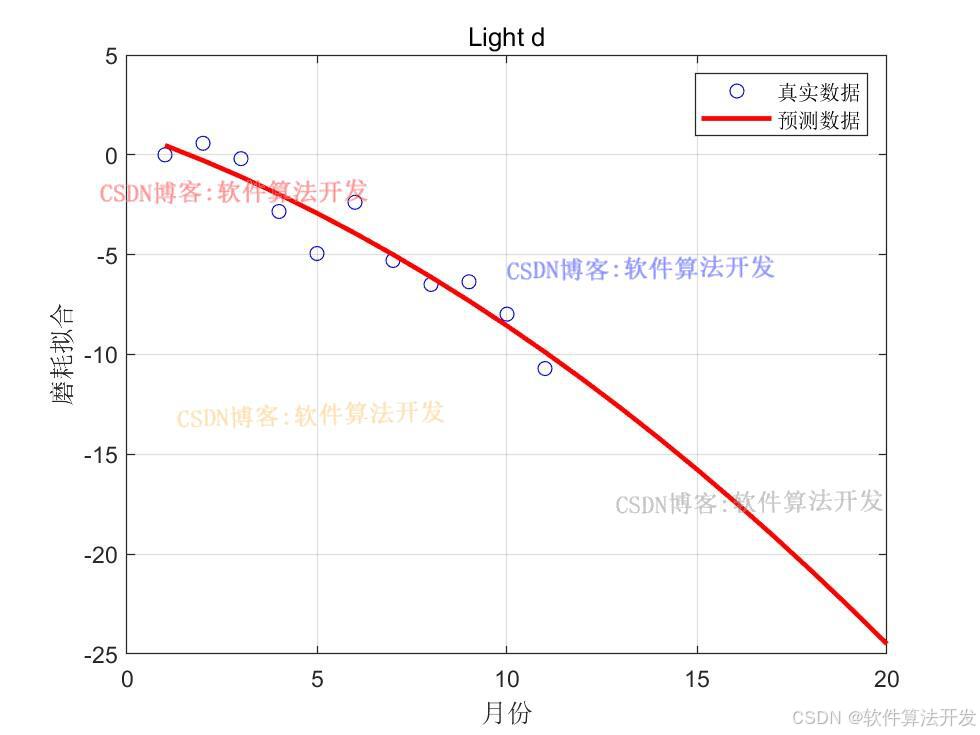
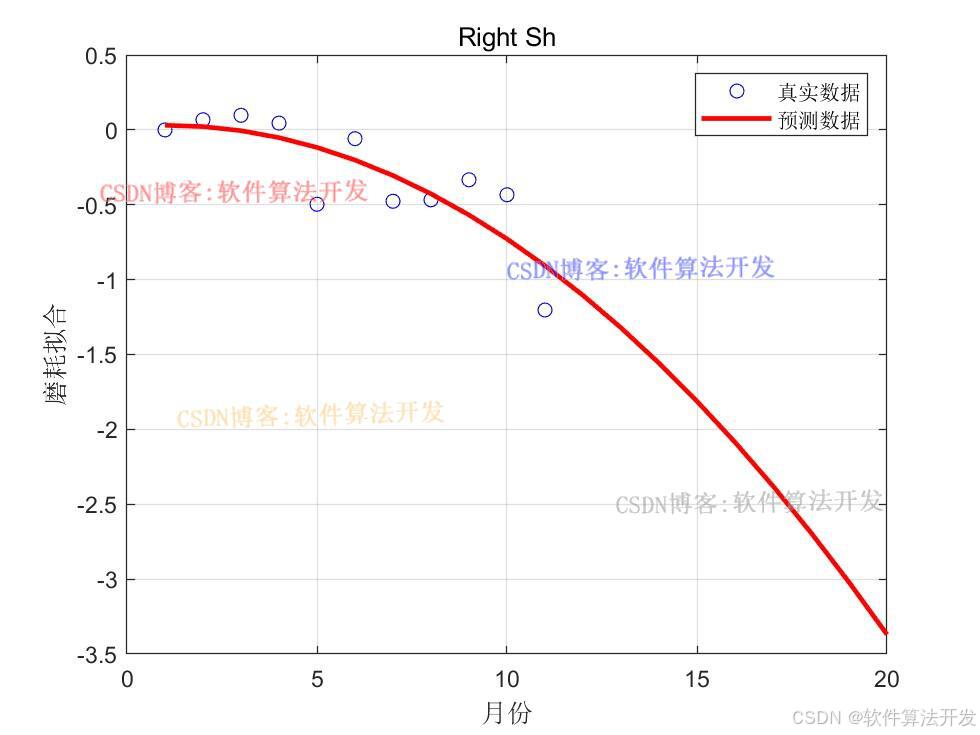
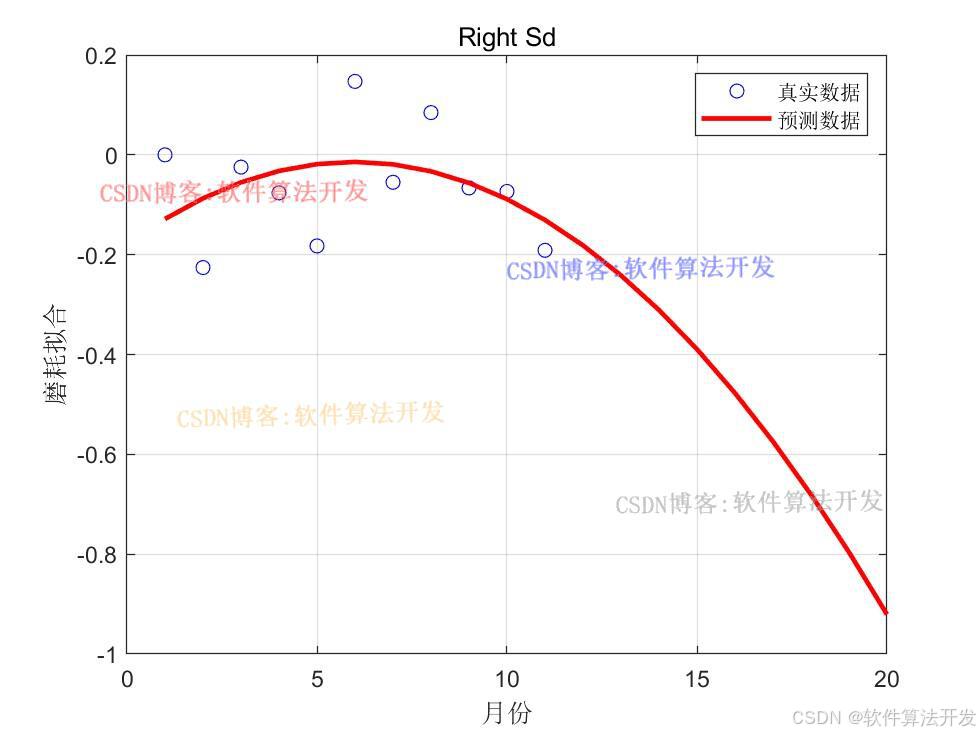
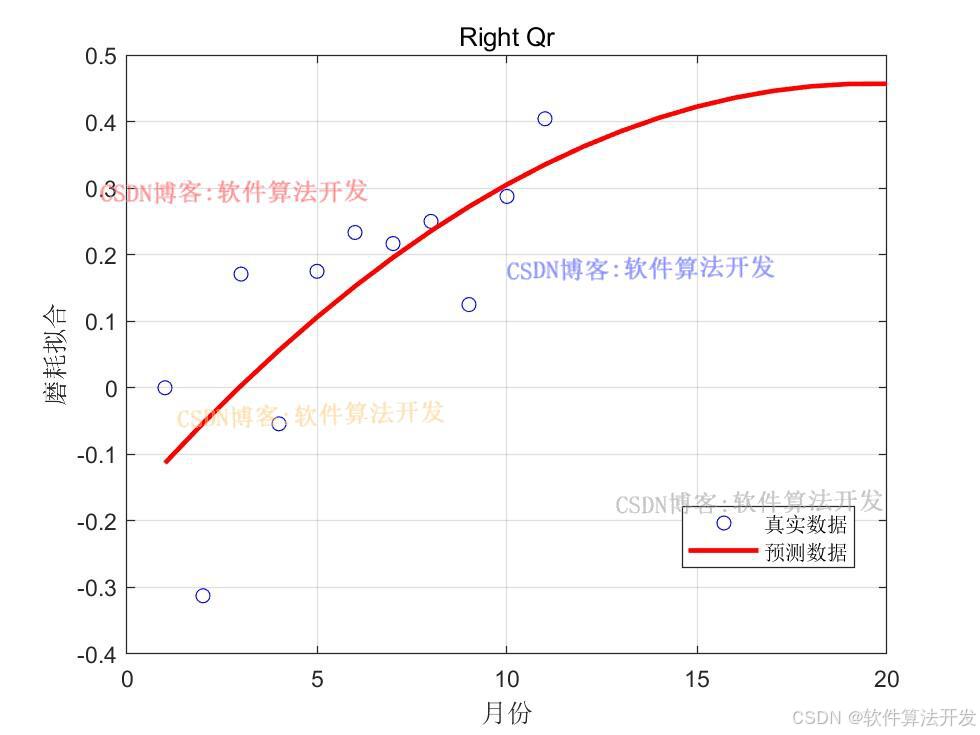
3.核心程序
....................................................
%%
while gen < MAXGEN;
%遗传算法选择交叉变异
if gen <= 1
Pe0 = 0.975;
pe1 = 0.025;
else
Pe0 = 1/(1+exp(-0.65*df));
pe1 = 1-Pe0;
end
FitnV=ranking(Objv);
Selch=select('sus',Chrom,FitnV);
Selch=recombin('xovsp', Selch,Pe0);
Selch=mut( Selch,pe1);
phen1=bs2rv(Selch,FieldD);
for a=1:1:NIND
Sh_{a} = phen1(a,1:2*Cnums);
Sd_{a} = phen1(a,2*Cnums+1:4*Cnums);
Qr_{a} = phen1(a,4*Cnums+1:6*Cnums);
D_{a} = phen1(a,6*Cnums+1:8*Cnums);
%计算对应的目标值
[epls,Couts] = func_obj(Sh_{a},Sd_{a},Qr_{a},D_{a},Sdr,Sdp);
E = epls;
JJ(a,1) = E;
JJc(a,1) = Couts;
end
Objvsel=(JJ);
[Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);
gen=gen+1;
%保存参数收敛过程和误差收敛过程以及函数值拟合结论
index1 = isnan(JJ);
index2 = find(index1 == 1);
JJ(index2) = [];
Error2(gen) = min(JJ);
[VV,II]=min(JJ);
df = max(Objvsel) - mean(Objvsel);
end
%根据优化结果得到优化的参数数据获得优化后的待优化变量值
[VV,II] = min(JJ);
Lsh_opt = Sh_{II}(1:Cnums);
Rsh_opt = Sh_{II}(Cnums+1:2*Cnums);
Lsd_opt = Sd_{II}(1:Cnums);
Rsd_opt = Sd_{II}(Cnums+1:2*Cnums);
Lqr_opt = Qr_{II}(1:Cnums);
Rqr_opt = Qr_{II}(Cnums+1:2*Cnums);
LD_opt = D_{II}(1:Cnums);
RD_opt = D_{II}(Cnums+1:2*Cnums);
SM(mtkl)= min(JJ);
SM2(mtkl)= JJc(II);
end
EL(timdx) = R/Len*mean(SM)/NLc;
ELc(timdx) = mean(SM2);
end
%计算得到使用寿命
ELs(cl) = 1e1*mean(EL);
%期望镟修次数
NELs(cl) = round(5e3*mean(ELc)/NLc/Sdr);
end
subplot(312);
plot(ELs,'b-*');
grid on
ylabel('期望使用寿命');
subplot(313);
plot(NELs,'b-*');
grid on
ylabel('期望璇修次数');
save R22.mat ELs NELs
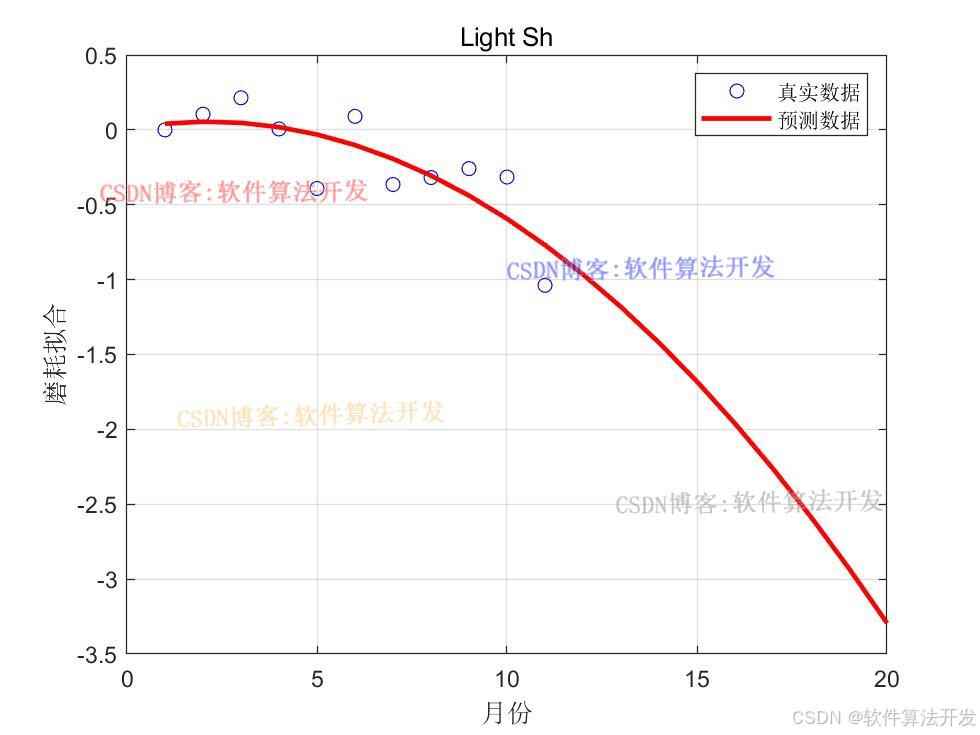
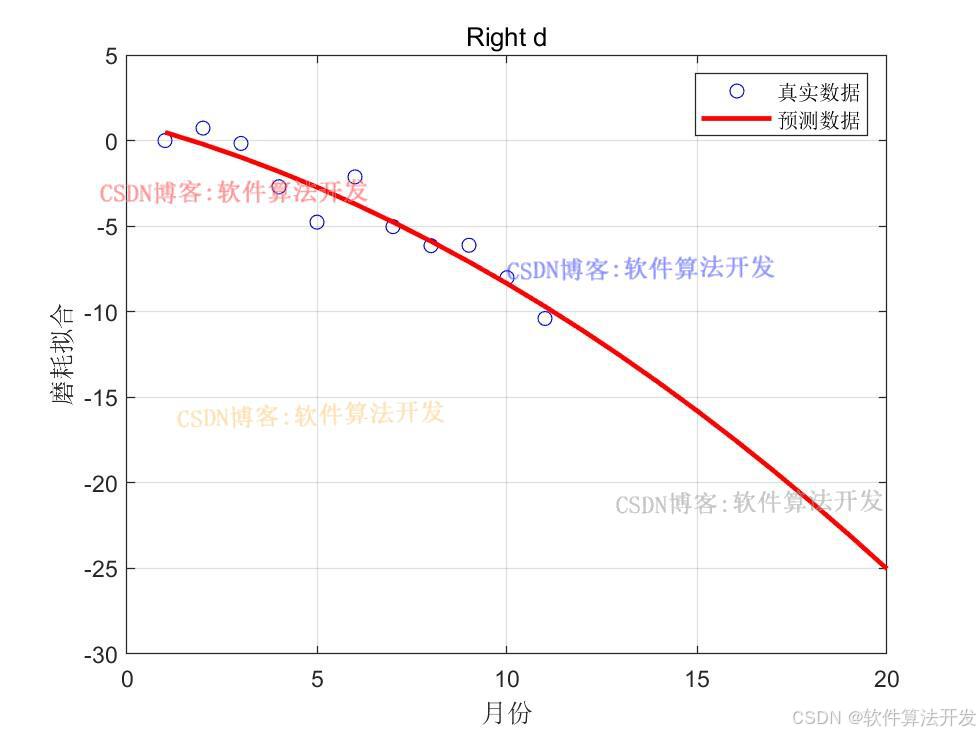
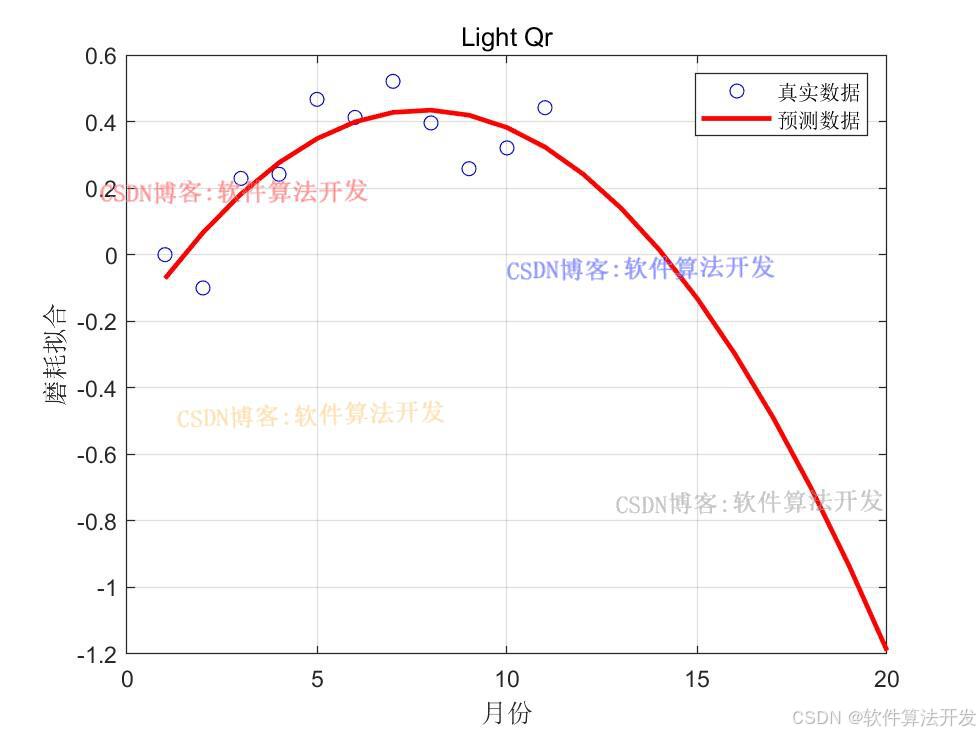
forcast;
16_074m4.本算法原理
传统遗传算法中交叉概率和变异概率通常是固定的,而自适应遗传算法则根据种群中个体的适应度值动态调整这两个概率。在优化初期,为了广泛探索解空间,适应度较差的个体采用较高的交叉率和变异率,以增加新个体的产生和多样性;在接近最优解时,适应度较高的个体采用较低的变异率,以保护优良基因,同时也能进行局部精细搜索,避免错过最优解。这种自适应调整可以在全局搜索和局部搜索之间取得平衡,提高算法的优化效率和精度,避免早熟收敛。
自适应交叉率根据个体的适应度值进行调整。如果两个个体的适应度较差,则使用较高的交叉率增加探索范围;如果两个个体的适应度较好,则降低交叉率以保留优良个体。
变异率同样根据个体的适应度进行动态调整。适应度较差的个体采用较高的变异率,适应度较高的个体采用较低的变异率,以保护优秀基因。
一般情况下,当交叉概率的值较大的时候,那么种群中新的个体的诞生速度较快,从而使得种群具有多样性;而当交叉概率的值较小的时候,则种群中新的个体诞生的速度较慢。通过上面的分析可知,交叉概率和变异概率是影响遗传算法性能的主要因素。通过自适应调整的方式来获得交叉概率和变异概率从而保证种群中各个个体的多样性:

根据以上原理和步骤,以及各个个体染色体的基本情况,通过自适应调整的方式进行交叉概率以及变异概率的调整。其中,在遗传算法中,对交叉和变异方式的判断,其主要通过每个个体的染色体最大适应度值以及平均适应度的差值来计算.
5.完整程序
VVV