哈喽，大家好。我是我不是小upper~
今天和大家聊聊结合 ARIMA 与贝叶斯回归的时间序列预测及不确定性分析。这个话题听起来有点专业，但咱们可以一步步拆解清楚～
首先得从ARIMA 模型 说起。ARIMA（自回归积分滑动平均模型）是时间序列预测的经典方法，它擅长捕捉数据中的趋势性 和周期性。比如，通过分析过去几年的月度销售额，ARIMA 能基于历史数据的 "自相关性"（过去值与当前值的关联）和 "滑动平均"（误差项的相关性）来拟合序列规律，从而预测未来趋势。不过，ARIMA 有个局限：它假设模型参数是固定的，且预测结果通常是一个 "点估计"（比如预测下个月销售额为 100 万元），但现实中，这种预测往往伴随着不确定性 ------ 比如实际销售额可能在 90 万到 110 万之间波动，而 ARIMA 本身难以量化这种波动范围。
这时候，贝叶斯回归 就能派上用场了。贝叶斯方法的核心是用 "概率分布" 来描述参数的不确定性。举个例子，传统回归模型会给出一个固定的参数值（如斜率为 2.5），而贝叶斯回归会说："斜率服从均值为 2.5、标准差为 0.3 的正态分布"。这种特性让贝叶斯方法能将先验知识 （比如行业经验判断）与观测数据 结合，通过贝叶斯定理更新参数的后验分布，最终不仅能给出预测值，还能输出预测的置信区间（如 "下个月销售额有 95% 的概率在 90 万到 110 万之间"）。
当我们把 ARIMA 与贝叶斯回归结合时，简单来说，其实是在做两件事：
- 用 ARIMA 建模时间序列的结构化特征：比如趋势、季节性等，将序列转化为平稳序列后，用自回归和滑动平均项捕捉短期依赖关系。
- 用贝叶斯框架处理模型参数的不确定性：ARIMA 的参数（如自回归阶数 p、滑动平均阶数 q）和误差项的方差，在贝叶斯视角下都可以视为随机变量，通过马尔可夫链蒙特卡罗（MCMC）等方法对这些变量进行抽样，从而得到包含不确定性的预测分布。
这里简单介绍一下相关的三个方面：
1. ARIMA 模型：时间序列的结构化建模
ARIMA（自回归积分滑动平均模型）是时间序列分析中的经典方法，特别适用于具有趋势或季节性的数据建模。其核心思想是通过三个步骤分解序列特征：
- 差分（I, Integrated） ：对非平稳序列进行 d 阶差分（如一阶差分
），消除趋势或季节性，使其变为平稳序列
- 自回归（AR, Autoregressive） ：假设平稳序列
- 滑动平均（MA, Moving Average） ：引入前 q 期白噪声的线性组合，描述序列的短期相关性：
2. 贝叶斯回归模型：带不确定性的参数推断
贝叶斯回归是传统线性回归的概率扩展，核心在于将参数视为随机变量，通过先验分布和观测数据更新后验分布，公式框架为： 线性模型 ： 贝叶斯视角：
- 先验分布 ：对参数
- 后验分布 ：根据贝叶斯定理，结合似然函数
3. ARIMA 与贝叶斯回归的融合思路
将两种方法结合，可同时捕捉时间序列的线性结构与非线性残差模式，提升预测精度并量化不确定性。以下是两种典型融合方式：
3.1 分步建模：ARIMA 捕捉线性趋势 + 贝叶斯回归拟合残差
步骤 1：ARIMA 提取序列的线性成分
- 对原始序列
- 残差性质 ：理想情况下
步骤 2：贝叶斯回归建模残差
- 将残差
- 通过贝叶斯推断估计
最终预测 ： 不确定性整合 ：总预测方差为 ARIMA 残差方差与贝叶斯回归预测方差之和，即
3.2 整体建模：将 ARIMA 嵌入贝叶斯框架
直接在贝叶斯框架下联合估计 ARIMA 参数与回归参数，公式为：
优势：
- 通过马尔可夫链蒙特卡洛（MCMC，如 Gibbs 采样）同时估计 ARIMA 参数 (
- 自然融合参数不确定性，直接输出包含趋势、回归效应和随机波动的全概率预测分布：
4. 不确定性分析详解
-
ARIMA 的预测区间 假设残差
-
贝叶斯回归的预测分布 预测值
-
融合模型的不确定性传播 结合 ARIMA 与贝叶斯回归的误差项独立性假设，最终预测的标准差为：
5. 基于 ARIMA 与贝叶斯回归的时间序列联合预测完整案例
这里，咱们整个流程包括：数据生成、ARIMA模型训练、残差贝叶斯回归建模、预测及不确定性分析~
假设我们有一段时间序列数据，其趋势和季节性可由ARIMA模型较好拟合，但存在复杂的非线性残差。通过对ARIMA残差使用贝叶斯回归建模，可以捕捉隐藏的结构或外生变量影响，并获得完整的预测分布，从而实现更准确和更有不确定性度量的预测。
数据集
生成一个包含趋势、季节性和随机非线性残差的时间序列：
-
时间序列长度：500
-
趋势：线性上升
-
季节性：正弦波
-
非线性残差：依赖于前几个时刻值 + 噪声
ARIMA模型训练与预测
使用 statsmodels 实现ARIMA(p,d,q)模型。p,d,q参数选择简单，主要为了提取主趋势和季节性。
贝叶斯回归对残差建模
利用PyTorch实现贝叶斯线性回归，采用变分推断（Variational Inference）进行参数估计。输入是ARIMA残差的若干滞后项，输出是残差的预测值。
联合预测与不确定性分析
-
ARIMA给出主预测趋势
-
贝叶斯回归对残差进行预测，产生预测分布
-
结合两者预测和方差，获得最终预测区间
数据可视化与分析解读
绘制包括：
-
原始时间序列与ARIMA预测对比图
-
残差时间序列与贝叶斯回归预测对比图
-
预测区间覆盖图（联合模型）
-
预测残差分布及不确定性示意图
算法优化与调参流程
-
ARIMA参数自动选择
-
贝叶斯模型先验设计与变分推断优化
-
避免数据泄露的时间序列交叉验证方案
代码实现：生成虚拟数据
python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.tsa.arima.model import ARIMA
import torch
import torch.nn as nn
import torch.optim as optim
sns.set(style="darkgrid")
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['axes.titlesize'] = 16
# 2. 生成虚拟数据集
np.random.seed(2025)
T = 500
time = np.arange(T)
# 趋势：线性上升
trend = 0.05 * time
# 季节性：12周期正弦波
seasonality = 2 * np.sin(2 * np.pi * time / 12)
# 非线性残差（依赖前两时刻的非线性组合 + 高斯噪声）
residuals = np.zeros(T)
for t in range(2, T):
residuals[t] = 0.5 * np.sin(residuals[t-1]) - 0.3 * residuals[t-2] + np.random.normal(0, 0.5)
# 合成时间序列
y = trend + seasonality + residuals
# 转为DataFrame方便观察
data = pd.DataFrame({'time': time, 'y': y})
# 绘制原始序列
plt.figure()
plt.plot(time, y, color='deepskyblue', lw=2)
plt.title('Original Time Series with Trend and Seasonality', fontsize=18)
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()
# 3. ARIMA模型训练与预测
# 简单设置ARIMA参数(p,d,q) = (2,0,2)
model = ARIMA(y, order=(2,0,2))
arima_res = model.fit()
print(arima_res.summary())
# ARIMA预测（前向一步预测）
y_pred_arima = arima_res.predict()
# 绘制ARIMA拟合效果
plt.figure()
plt.plot(time, y, label='Actual', color='deepskyblue', lw=2)
plt.plot(time, y_pred_arima, label='ARIMA Prediction', color='orangered', lw=2)
plt.title('ARIMA Fit vs Actual', fontsize=18)
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()
# 计算残差
residual_arima = y - y_pred_arima
plt.figure()
plt.plot(time, residual_arima, color='mediumvioletred', lw=1)
plt.title('Residuals after ARIMA', fontsize=18)
plt.xlabel('Time')
plt.ylabel('Residual')
plt.show()
# 4. 贝叶斯回归对残差建模
# 数据准备: 用残差的前2个滞后项作为特征预测当前残差
lag = 2
X = []
Y = []
for t in range(lag, T):
X.append(residual_arima[t-lag:t])
Y.append(residual_arima[t])
X = np.array(X)
Y = np.array(Y)
# 转为torch tensor
X_tensor = torch.tensor(X, dtype=torch.float32)
Y_tensor = torch.tensor(Y, dtype=torch.float32).view(-1, 1)
# 贝叶斯线性回归类 (变分推断框架)
class BayesianLinearRegressionVI(nn.Module):
def __init__(self, input_dim):
super().__init__()
# 参数先验的均值与log方差，用于变分推断
self.mu_weight = nn.Parameter(torch.zeros(input_dim, 1))
self.log_var_weight = nn.Parameter(torch.zeros(input_dim, 1))
self.mu_bias = nn.Parameter(torch.zeros(1))
self.log_var_bias = nn.Parameter(torch.zeros(1))
self.log_noise_var = nn.Parameter(torch.tensor(0.0)) # 噪声log方差
def forward(self, x, sample=False):
if sample:
# 采样权重和偏置
weight = self.mu_weight + torch.exp(0.5 * self.log_var_weight) * torch.randn_like(self.mu_weight)
bias = self.mu_bias + torch.exp(0.5 * self.log_var_bias) * torch.randn_like(self.mu_bias)
else:
weight = self.mu_weight
bias = self.mu_bias
return x @ weight + bias
def kl_divergence(self):
# 计算KL散度，正态分布KL散度公式
kl_w = -0.5 * torch.sum(1 + self.log_var_weight - self.mu_weight**2 - torch.exp(self.log_var_weight))
kl_b = -0.5 * torch.sum(1 + self.log_var_bias - self.mu_bias**2 - torch.exp(self.log_var_bias))
return kl_w + kl_b
# 训练函数
def train_vi(model, x, y, epochs=2000, lr=0.01):
optimizer = optim.Adam(model.parameters(), lr=lr)
n = x.shape[0]
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
# 预测均值
pred = model(x, sample=False)
# 负对数似然
noise_var = torch.exp(model.log_noise_var)
nll = 0.5 * torch.sum((y - pred)**2 / noise_var + torch.log(noise_var))
# KL散度
kl = model.kl_divergence()
# 变分下界loss (ELBO)
loss = nll + kl / n
loss.backward()
optimizer.step()
if (epoch+1) % 500 == 0 or epoch == 0:
print(f'Epoch {epoch+1}/{epochs} - Loss: {loss.item():.4f}')
return model
# 模型实例化与训练
blr_vi = BayesianLinearRegressionVI(input_dim=lag)
blr_vi = train_vi(blr_vi, X_tensor, Y_tensor, epochs=2000, lr=0.01)
# 5. 联合预测与不确定性分析
# ARIMA预测残差部分的贝叶斯预测（采样多次估计不确定性）
def bayesian_predict(model, x, samples=100):
model.eval()
preds = []
for _ in range(samples):
pred = model(x, sample=True).detach().cpu().numpy()
preds.append(pred)
preds = np.array(preds).squeeze() # shape: (samples, N)
mean_pred = preds.mean(axis=0)
std_pred = preds.std(axis=0)
return mean_pred, std_pred
mean_res_pred, std_res_pred = bayesian_predict(blr_vi, X_tensor, samples=200)
# 构造联合预测：ARIMA预测 + 贝叶斯残差预测
y_pred_joint = y_pred_arima[lag:] + mean_res_pred
time_pred = time[lag:]
# 联合不确定性（假设独立方差叠加）
arima_sigma = np.sqrt(arima_res.scale)
joint_std = np.sqrt(arima_sigma**2 + std_res_pred**2)
# 6. 可视化联合预测及不确定性
plt.figure()
plt.plot(time, y, label='Actual', color='deepskyblue', lw=2)
plt.plot(time, y_pred_arima, label='ARIMA Prediction', color='orangered', lw=1.5, alpha=0.7)
plt.plot(time_pred, y_pred_joint, label='Combined Prediction', color='mediumseagreen', lw=2)
plt.fill_between(time_pred,
y_pred_joint - 2 * joint_std,
y_pred_joint + 2 * joint_std,
color='mediumseagreen', alpha=0.3, label='95% Prediction Interval')
plt.title('Combined ARIMA + Bayesian Regression Prediction with Uncertainty', fontsize=18)
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()
# 预测残差分布与不确定性可视化
plt.figure()
plt.errorbar(time_pred, mean_res_pred, yerr=2*std_res_pred,
fmt='o', color='mediumvioletred', ecolor='palevioletred', elinewidth=2, capsize=3)
plt.title('Bayesian Regression Residual Predictions with Uncertainty', fontsize=18)
plt.xlabel('Time')
plt.ylabel('Residual Prediction')
plt.show()
# ARIMA残差自相关图，观察残差序列中的结构性
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(residual_arima[lag:], lags=40, title='Autocorrelation of ARIMA Residuals')
plt.show()
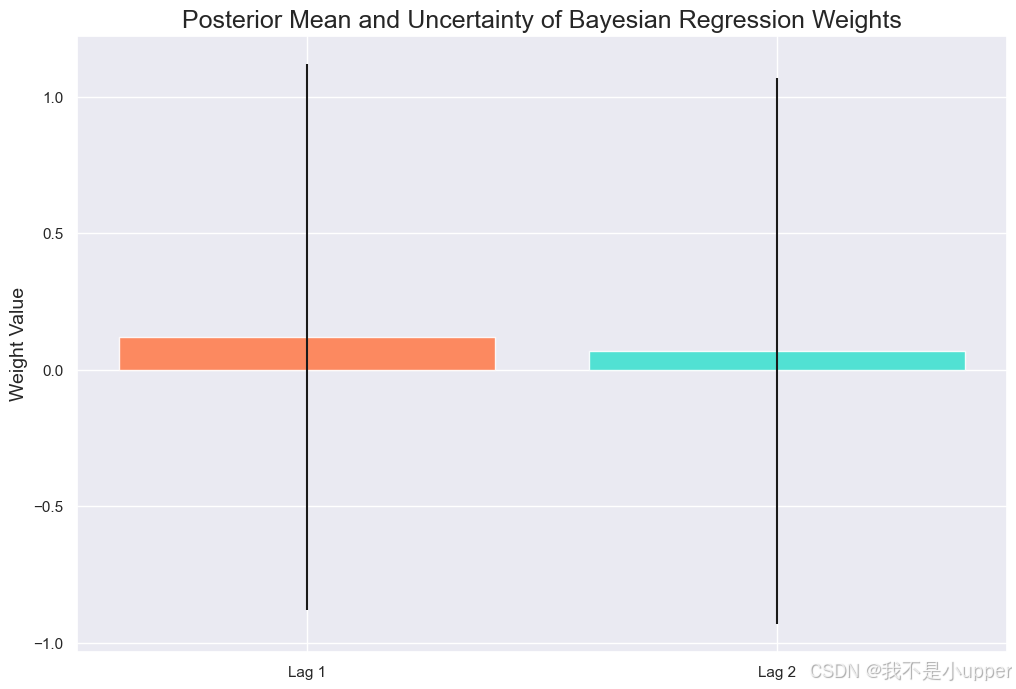
# 贝叶斯回归权重后验分布（均值与方差）
plt.figure()
plt.bar(['Lag 1', 'Lag 2'], blr_vi.mu_weight.detach().squeeze().numpy(),
yerr=torch.exp(0.5 * blr_vi.log_var_weight).detach().squeeze().numpy(),
color=['coral', 'turquoise'], alpha=0.9)
plt.title('Posterior Mean and Uncertainty of Bayesian Regression Weights', fontsize=18)
plt.ylabel('Weight Value')
plt.show()
1. Original Time Series with Trend and Seasonality：显示虚拟数据的整体结构，包括线性趋势和明显的季节波动，模拟真实世界中很多时间序列的典型特征。
2. ARIMA Fit vs Actual：展示ARIMA模型对时间序列的拟合效果，能捕捉主要趋势和季节性，但仍存在系统残差。
3. Residuals after ARIMA：画出ARIMA残差，便于分析未被ARIMA解释的部分，观察是否存在自相关或结构。
4. Combined ARIMA + Bayesian Regression Prediction with Uncertainty：显示两阶段联合模型的预测结果及95%置信区间，体现预测效果提升与不确定性度量。
5. Bayesian Regression Residual Predictions with Uncertainty：贝叶斯回归对残差的预测及置信区间，展示模型如何捕获残差的动态不确定性。
6. Autocorrelation of ARIMA Residuals：检验残差的自相关性，若存在显著的自相关，则贝叶斯回归的建模是合理且必要的。
7. Posterior Mean and Uncertainty of Bayesian Regression Weights：贝叶斯回归权重的后验分布，反映各滞后变量对残差的贡献及参数估计不确定性。
算法优化与调参流程
在算法优化与调参流程中，ARIMA 模型的参数优化需借助统计指标与数据特性的双重考量。具体而言，通过 AIC（赤池信息准则）和 BIC（贝叶斯信息准则）自动搜索最优的 (p,d,q) 组合，这一过程旨在平衡模型的拟合优度与复杂度 ------AIC 和 BIC 通过对模型参数数量施加 "惩罚项"，避免因参数过多导致过拟合，或因参数过少引发欠拟合。其中，差分阶数 d 的调整是关键环节：通过对原始时间序列进行 d 阶差分，使数据满足平稳性要求（如均值、方差不随时间变化），这是 ARIMA 模型有效建模的前提。在验证模型泛化能力时，采用时间序列特有的交叉验证方法，例如滚动预测（rolling forecast）或递归划分训练集与验证集，确保在参数调优过程中不泄露未来数据信息，避免高估模型的预测性能。
贝叶斯回归的调优则需从先验设定与推断过程两方面入手。在先验选择阶段，可依据领域知识为模型参数指定合理的先验均值和方差（如已知某物理量的取值范围），若缺乏先验信息，也可采用非信息先验（如正态分布的宽方差设置），以减少先验对后验推断的过度影响。为提升模型的拟合能力，可尝试引入更多滞后项（捕捉历史数据的依赖关系）或外生变量（如相关经济指标、环境因素），将单变量模型扩展为多元贝叶斯回归模型。在变分推断过程中，通过调整学习率优化近似后验的收敛速度，或采用更复杂的变分分布（如 Normalizing Flows）提升对多模态后验的拟合精度。此外，合理调节马尔可夫链蒙特卡罗（MCMC）的采样次数或变分推断的迭代次数，确保预测分布的稳定性，避免因采样不足导致后验估计存在较大方差。
本案例通过构造虚拟时间序列数据，完整展示了 ARIMA 与贝叶斯回归的结合流程：ARIMA 模型负责捕捉数据中的趋势与季节性模式，贝叶斯回归则用于建模残差中的非线性结构，并通过概率分布量化预测不确定性。值得一提的是，基于 PyTorch 的变分贝叶斯实现，借助其自动微分与动态图特性，为贝叶斯模型的高效推断提供了灵活的工具，可便捷地处理复杂先验与高维参数空间的优化问题。