[面试精选] 0094. 二叉树的中序遍历

文章目录

• • • [1. 题目链接](#1. 题目链接)
    • [2. 题目描述](#2. 题目描述)
    • [3. 题目示例](#3. 题目示例)
    • [4. 解题思路](#4. 解题思路)
    • [5. 题解代码](#5. 题解代码)
    • [6. 复杂度分析](#6. 复杂度分析)

1. 题目链接

94. 二叉树的中序遍历 - 力扣（LeetCode）

2. 题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

3. 题目示例

示例 1 :

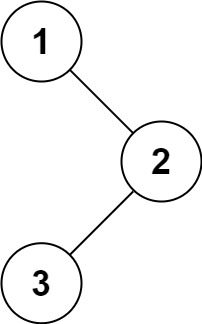
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2 :

输入：root = []
输出：[]

4. 解题思路

1. 颜色标记法 ：
   • 使用颜色标记节点状态：1（未访问）、2（已访问）
   • 模拟递归栈的调用过程，但通过显式栈实现
2. 栈操作顺序 ：
   • 对于未访问节点（color=1），按"右-根-左"顺序入栈
   • 这样出栈顺序就是"左-根-右"，符合中序遍历要求
3. 关键点 ：
   • 通过颜色标记避免重复处理
   • 显式栈替代递归调用栈
   • 空节点直接跳过

5. 题解代码

class Solution {
    // 辅助节点类，用于标记节点状态
    class Node {
        TreeNode node;  // 树节点
        int color;      // 颜色标记：1表示未访问，2表示已访问

        Node(TreeNode node, int color) {
            this.node = node;
            this.color = color;
        }
    }

    // 中序遍历方法
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();  // 存储遍历结果
        Deque<Node> stack = new LinkedList<>();  // 使用双端队列模拟栈
        
        // 空树直接返回
        if (root == null) return ans;
        
        // 初始状态：根节点标记为未访问
        stack.push(new Node(root, 1));
        
        while (!stack.isEmpty()) {
            Node cur = stack.pop();  // 弹出栈顶元素
            
            // 跳过空节点
            if (cur.node == null) continue;
            
            if (cur.color == 1) {  // 未访问节点
                // 按照"右-根-左"顺序入栈（出栈顺序为"左-根-右"）
                stack.push(new Node(cur.node.right, 1));  // 右子节点（未访问）
                stack.push(new Node(cur.node, 2));        // 当前节点标记为已访问
                stack.push(new Node(cur.node.left, 1));   // 左子节点（未访问）
            } else {  // 已访问节点
                ans.add(cur.node.val);  // 添加到结果列表
            }
        }
        return ans;
    }
}

6. 复杂度分析

1. 时间复杂度 ：O(n)
   • 每个节点被访问两次（入栈和出栈）
   • 但常数系数为2，仍为线性复杂度
2. 空间复杂度 ：O(n)
   • 栈的最大深度等于树的高度
   • 最坏情况下（斜树）为O(n)