树，森林
树的存储结构
双亲表示法
把他们的爹写上去
然后他们用的是连续的空间
孩子表示法
把孩子变成一个链表！？！这里就是图的邻接表
用编号代表，因为A，B，C这种有时候会很大
孩子，兄弟！表示法
只有一个孩子，后面全是兄弟
下面例子
R我只有一个孩子就是A，放左边
A：剩下的BC是我兄弟！往右边放，然后我有一个孩子D
D：我没有孩子，我是反生育主义，我觉得这个世界糟透了，但我有兄弟E，放在了右边
然后是全部展示
变成二叉树了
还原也要会
森林转二叉树
转
先用孩子兄弟把每颗树给整一下子，然后可以发现A是孩子，BC是A的兄弟
反转
反向也要会转
然后我们可以看见，如果只是单纯的一棵树，是不会有右边的
所以一旦有右边那它就会是森林
还是这个图，A右边包括自己有3个节点，说明有3颗树
做题
1
c
2
b
3
这种情况的题目最好具象化，特殊值做法
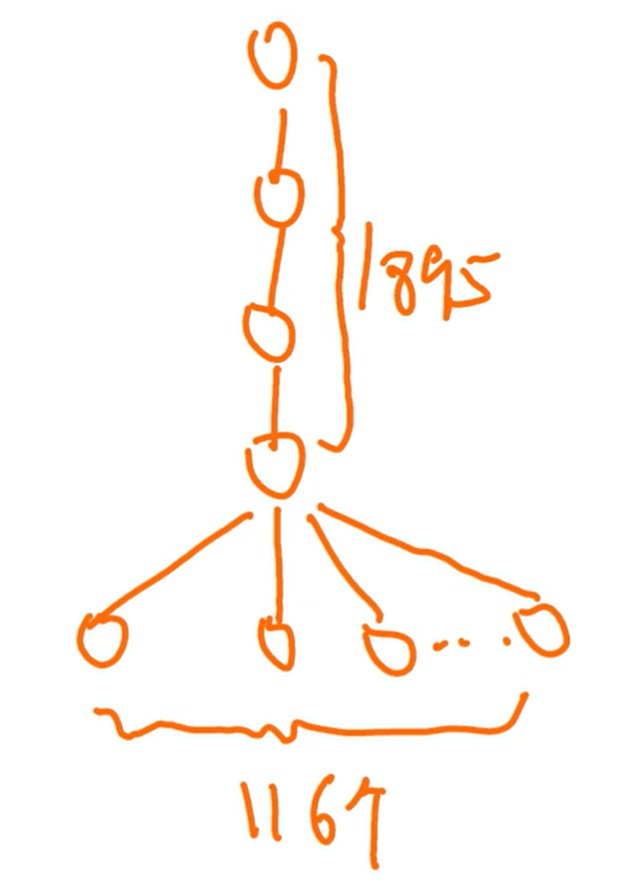最后一个兄弟挺多，1895个
但别忘了最后一个右节点也没有右孩子
所以选D
树和森林的遍历
理解
下面是对应关系
举例子就知道了
这里想要求树的后序，就可以求二叉树的中序
想要求树的遍历，就得求二叉树的遍历
做题
1
性质
b
2
这里给了森林的先和后，就是二叉树的先和中
做一下
c
哈夫曼树
理解
注意结点的带权路径长度和树的带权路径长度
这里该节点（比如6）的带权路径长度就是6 * 2
树的带权路径长度就是所有叶子节点
这里WPL记一下，带权路径长度缩写
哈夫曼树不存在度为1的
做题
1
可以养成个好习惯，选完2个最小的 就小的放左边，大的放右边
200，没毛病
b
2
公式 n0 = n2 + 1
因为哈夫曼树中最初构造的节点最终都会落到叶结点上，所以这里n=n0，因此可以算出n2 = n-1
然后就是哈夫曼只有n0和n2
就是n0 + n2 = 115 n + n-1 = 115 n= 58
c
哈夫曼编码
前缀编码
什么意思？直接做题
可以看见110与1100是重合的，所以不是前缀编码
编码
哈夫曼编码是左0 右1
做题
1
太简单
d
2
然后WPL是
这里WPL的意义是，整个哈夫曼树二进制的总个数
a
可变长度编码和固定长度编码
哈夫曼是可变长度编码
只有在同一层才是固定长度编码
然后就是可变长编码与固定编码的压缩比
可以对比这2张图，第二张图是固定编码（6个在同一层）
他们的WPL压缩比就是1 - （224 / 300）大概是25%
做题
1
假设n = 3，2个图是这样的
定长所有字符在都同一层
选D哈
2
不就画吗
发现10和10并不能组成24
这里c选项的问题是0和3最小的没有画一块
D很爽，选就完了
并查集
09年之后从未在真题中出现过，请务必重视！（开玩笑的）