数据结构之二叉树

系列文章目录

数据结构之ArrayList-CSDN博客

数据结构之LinkedList-CSDN博客

数据结构之栈-CSDN博客

数据结构之队列-CSDN博客

---

目录

系列文章目录

前言

一、二叉树的性质

二、二叉树的基本操作

[1. 前中后序遍历](#1. 前中后序遍历)

[2. 发现重复子问题的思路](#2. 发现重复子问题的思路)

[3. 层序遍历](#3. 层序遍历)

[4. 判断完全二叉树](#4. 判断完全二叉树)

三、二叉树常见题目

[1. 判断是否是相同的树](#1. 判断是否是相同的树)

[2. 判断是否是子树](#2. 判断是否是子树)

[3. 翻转二叉树](#3. 翻转二叉树)

[4. 判断平衡二叉树](#4. 判断平衡二叉树)

[5. 对称二叉树](#5. 对称二叉树)

[6. 创建二叉树](#6. 创建二叉树)

[7. 找两个节点的最近公共祖先](#7. 找两个节点的最近公共祖先)

[8. 根据前序遍历和中序遍历构建二叉树](#8. 根据前序遍历和中序遍历构建二叉树)

[9. 根据中序遍历和后续遍历构建二叉树](#9. 根据中序遍历和后续遍历构建二叉树)

[10. 根据二叉树创建字符串](#10. 根据二叉树创建字符串)

[11. 二叉树的非递归遍历](#11. 二叉树的非递归遍历)

---

前言

本文介绍二叉树的性质以及二叉树的基本操作，对于重复子问题使用递归的思想进行求解，以及二叉树常见题目的求解。

---

一、二叉树的性质

1. 若规定根节点的层数为 1，一棵非空二叉树的第 i 层最多有 2^(i - 1)个节点；

2. 若规定根节点的深度为 1，则深度为 k 的二叉树最大节点数为 2^k - 1；

3. 对于任意一棵二叉树，如果叶节点的个数为 n0，度为 2 的非叶节点的个数为 n2，则有 n0 = n2 + 1；

4. 具有 n 个节点的完全二叉树的深度为 log2(n + 1) 向上取整；

5. 对于有 n 个节点的完全二叉树，按照从上到下从左往右的顺序，从 0 开始编号，对于序号为 i 的节点：

1. 若 i > 0，父节点的编号为：(i - 1) / 2，若 i == 0，则该节点为根节点，无父节点；
2. 若 2 * i + 1 < n，左孩子节点为：2 * i + 1；
3. 若 2 * i + 2 < n，右孩子节点为：2 * i + 2；

二、二叉树的基本操作

二叉树的存储分为顺序存储和类似链表的链式存储。

下面以链式存储的方式实现：

public class BinaryTree {
    static class TreeNode{
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val){
            this.val = val;
        }
    }

    public TreeNode root;

    // ......
}

1. 前中后序遍历

不带返回值的递归实现：

preOrder(TreeNode root): void前序遍历；

inOrder(TreeNode root): void中序遍历；

postOrder(TreeNode root): void后续遍历；

    public void preOrder(TreeNode root){
        if(root == null) return;
        System.out.print(root.val + " ");
        preOrder(root.left);
        preOrder(root.right);
    }

    public void inOrder(TreeNode root){
        if(root == null) return;
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }

    public void postOrder(TreeNode root){
        if(root == null) return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val + " ");
    }

带返回值的递归实现：

**preorderTraversal(TreeNode root): List<Integer>**前序遍历;

**inorderTraversal(TreeNode root): List<Integer>**中序遍历;

**postorderTraversal(TreeNode root): List<Integer>**后序遍历;

要点是如何在递归过程中利用返回值：利用 List 接口的 addAll() 方法，将子树的结果收集起来；

public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if(root == null) return ret;
        ret.add(root.val);
        List<Integer> left = preorderTraversal(root.left);
        ret.addAll(left);
        List<Integer> right = preorderTraversal(root.right);
        ret.addAll(right);
        return ret;
    }

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if(root == null) return ret;
        List<Integer> left = inorderTraversal(root.left);
        ret.addAll(left);
        ret.add(root.val);
        List<Integer> right = inorderTraversal(root.right);
        ret.addAll(right);
        return ret;
    }

    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if(root == null) return ret;
        List<Integer> left = postorderTraversal(root.left);
        ret.addAll(left);
        List<Integer> right = postorderTraversal(root.right);
        ret.addAll(right);
        ret.add(root.val);
        return ret;
    }

2. 发现重复子问题的思路

size(TreeNode root): int 求树节点的个数；

getLeafNodeCount(TreeNode root): int 求叶子节点的个数；

getKLevelNodeCount(TreeNode root): int 求第 k 层节点的个数；

getHeight(TreeNode root): int 求树的高度；

find(TreeNode root, int val): TreeNode 找值为 val 的节点；

    // 获取树中节点的个数
    public int size(TreeNode root){
        if(root == null) return 0;
        return size(root.left) +
                size(root.right) + 1;
    }
    
    // 获取树中叶子节点的个数
    public int getLeafNodeCount(TreeNode root){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;
        return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
    }
    
    // 获取第 k 层节点的个数
    public int getKLevelNodeCount(TreeNode root, int k){
        if(root == null) return 0;
        if(k == 1) return 1;
        return getKLevelNodeCount(root.left, k - 1) + 
                getKLevelNodeCount(root.right, k - 1);
    }
    
    // 获取二叉树的高度
    public int getHeight(TreeNode root){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;
        return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
    }
    
    // 寻找值为 val 的节点
    public TreeNode find(TreeNode root, int val){
        if(root == null) return null;
        if(root.val == val) return root;
        TreeNode left = find(root.left, val);
        if(left != null) return left;
        else return find(root.right, val);
    }

3. 层序遍历

levelOrder(TreeNode root): void 不带返回值的层序遍历；

levelOrder(TreeNode root): List<List<TreeNode>> 将每一层元素放到一个子表中，返回总表；

**关键：**统计每一层元素的个数，将一层的元素都放到子表中，最终将子表加入到总表中；

    // 层序遍历
    public void levelOrder(TreeNode root){
        if(root == null) return;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode t = queue.poll();
            System.out.print(t.val + " ");
            if(t.left != null) queue.offer(t.left);
            if(t.right != null) queue.offer(t.right);
        }
        System.out.println();
    }

    // 带返回值的层序遍历
    public List<List<TreeNode>> levelOrder2(TreeNode root){
        List<List<TreeNode>> ret = new ArrayList<>();
        if(root == null) return ret;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int sz = queue.size();
            List<TreeNode> tmp = new ArrayList<>();
            while(sz-- > 0){
                TreeNode t = queue.poll();
                tmp.add(t);
                if(t.left != null) queue.offer(t.left);
                if(t.right != null) queue.offer(t.right);
            }
            ret.add(tmp);
        }
        return ret;
    }

4. 判断完全二叉树

isCompleteTree(TreeNode node): boolean 判断是否为完全二叉树；

使用层序遍历的思路，先将节点入队，弹出时，如果节点不为空，就将它的左右孩子入队；

如果弹出的节点为空，如果是完全二叉树，后续的节点应都为空；

遍历队列，如果弹出的节点不为空，就不是完全二叉树；

    public boolean isCompleteTree(TreeNode node){
        if(node == null) return true;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(node);
        while(!queue.isEmpty()){
            TreeNode t = queue.poll();
            if(t != null){
                queue.offer(t.left);
                queue.offer(t.right);
            }else{
                break;
            }
        }
        while(!queue.isEmpty()){
            TreeNode t = queue.poll();
            if(t != null) {
                return false;
            }
        }
        return true;
    }

三、二叉树常见题目

1. 判断是否是相同的树

isSameTree(TreeNode p, TreeNode q): boolean 判断 p 和 q 是否是同一棵树；

    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q == null) return true;
        if((p == null && q != null) || (p != null && q == null)) return false;
        if(p.val != q.val) return false;
        boolean left = isSameTree(p.left, q.left);
        if(!left) return false;
        boolean right = isSameTree(p.right, q.right);
        if(!right) return false;
        return true;
    }

2. 判断是否是子树

isSubTree(TreeNode root, TreeNode subTree): boolean 判断 subTree 是否是 root 的子树；

先判断 root 和 subTree 是否是相同的树，如果是返回 true；

如果不是，再判断 subTree 是否是 root.left 的子树，如果是返回 true；

如果也不是，再判断 subTree 是否是 root.right 的子树，如果是返回 true；

    // 判断是否是子树
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null) return false;
        boolean flag = isSameTree(root, subRoot);
        if(flag) return true;
        boolean left = isSubtree(root.left, subRoot);
        if(left) return true;
        boolean right = isSubtree(root.right, subRoot);
        if(right) return true;
        return false;
    }

    // 判断是否是相同的树
    private boolean isSameTree(TreeNode p, TreeNode q){
        if((p == null && q != null) || (p != null && q == null)) return false;
        if(p == null && q == null) return true;
        if(p.val != q.val) return false;
        boolean left = isSameTree(p.left, q.left);
        if(!left) return false;
        boolean right = isSameTree(p.right, q.right);
        if(!right) return false;
        return true;
    }

3. 翻转二叉树

invertTree(TreeNode root): TreeNode 翻转二叉树；

对于每一棵子树，左树放到右树的位置，右树放到左树的位置；

    public TreeNode invertTree(TreeNode root) {
        if(root == null) return null;
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }

4. 判断平衡二叉树

isBalanced(TreeNode root): boolean 判断是否是二叉树；

判断每一个子树是否是平衡二叉树：判断左右子树的高度，判断左右子树是否平衡；

    // 判断是否为平衡二叉树
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        int left = getHeight(root.left);
        int right = getHeight(root.right);
        if(Math.abs(left - right) > 1) return false;
        if(!isBalanced(root.left)) return false;
        if(!isBalanced(root.right)) return false;
        return true;
    }
    
    // 获取树的高度
    private int getHeight(TreeNode root){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;
        return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
    }

优化：

上述求解过程中，每个子树都要求高度，因此出现了大量的重复计算，时间复杂度为 O(n^2);

因此每次求高度的时候，要增加一个是否为平衡二叉树的判断，如果左右子树的高度差超过 1，返回 -1，表示非平衡子树，如果高度差小于等于 1，返回二叉树的高度；

这样在找高度的过程中就顺便判断了是否平衡，就不用再单独判断了；

    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        return dfs(root) > 0;
    }

    // 判断是否为平衡二叉树，并返回二叉树的高度
    public int dfs(TreeNode root){
        if(root == null) return 0;
        if(root.left == null && root.right == null) return 1;
        int left = dfs(root.left);
        if(left == -1) return -1;
        int right = dfs(root.right);
        if(right == -1) return -1;
        if(Math.abs(left - right) > 1) return -1;
        return Math.max(left, right) + 1;
    }

5. 对称二叉树

isSysmetric(TreeNode root): boolean 判断左右子树是否对称；

判断 t1 的左子树和 t2 的右子树是否相同，t1 的右子树和 t2 的左子树是否相同；

    public boolean isSymmetric(TreeNode root) {
        if(isSymmetricTree(root.left, root.right)){
            return true;
        }
        return false;
    }

    // 判断两个树是否对称
    public boolean isSymmetricTree(TreeNode t1, TreeNode t2){
        if(t1 == null && t2 == null) return true;
        if((t1 == null && t2 != null) || (t1 != null && t2 == null)) return false;
        if(t1.val != t2.val) return false;
        if(!isSymmetricTree(t1.left, t2.right)) return false;
        if(!isSymmetricTree(t1.right, t2.left)) return false;
        return true;
    }

6. 创建二叉树

createTree(char[] s): TreeNode 按照前序遍历的顺序创建二叉树（空节点用 '#' 表示）；

    // 按照前序遍历的顺序创建二叉树
    public int i;
    public TreeNode createTree(char[] s){
        TreeNode root = null;
        if(s[i] != '#'){
            root = new TreeNode(s[i]);
            i++;
            root.left = createTree();
            root.right = createTree();
        }else{
            i++;
        }
        return root;
    }

7. 找两个节点的最近公共祖先

lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q): TreeNode 找 p 节点和 q 节点的最近公共祖先；

两个节点要么分别在左子树和右子树，这种情况下，返回根节点即可；

要么都在左子树或者在右子树，这种情况下返回 p 或者 q；

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;
        if(root == p || root == q) return root;
        
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        if(left != null && right != null) return root;
        else if(left == null) return right;
        else return left;
    }

思路 2：

如果知道了 p 节点和 q 节点到 root 节点的路径，这个题目就变成了两个链表的第一个公共节点了。

求节点路径可以借助栈，当前节点不为空，入栈；

判断这个节点是不是要找的节点，如果是返回 true，表示找到了；

如果不是，去左子树找，如果找到了返回 true（可以递归）；

如果没找到，去右子树找，如果找到了，返回 true（可以递归）；

如果没找到，说明这个节点不是路径上的节点，出栈，并返回 false；

    // 找第一个公共节点
    public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;
        Stack<TreeNode> stackP = new Stack<>();
        Stack<TreeNode> stackQ = new Stack<>();
        getPath(root, p, stackP);
        getPath(root, q, stackQ);

        int sizeP = stackP.size();
        int sizeQ = stackQ.size();
        if(sizeP > sizeQ){
            while(sizeP != sizeQ){
                stackP.pop();
                sizeP--;
            }
        }else{
            while(sizeP != sizeQ){
                stackQ.pop();
                sizeQ--;
            }
        }

        while(stackP.peek() != stackQ.peek()){
            stackP.pop();
            stackQ.pop();
        }
        return stackP.peek();
    }

    // 找根节点到 node 的路径
    private boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack){
        if(root == null) return false;
        stack.push(root);
        if(root == node) return true;
        boolean left = getPath(root.left, node, stack);
        if(left) return true;
        boolean right = getPath(root.right, node, stack);
        if(right) return true;
        stack.pop();
        return false;
    }

8. 根据前序遍历和中序遍历构建二叉树

buildTree(int[] preorder, int[] inorder): TreeNode 根据前序遍历和中序遍历的数组创建二叉树；

createTreeByPreorderAndInorder(int[] preorder, int[] inorder, int begin, int end): TreeNode 根据前序遍历数组，在中序遍历数组中找根节点的下标，并创建根节点和左右孩子；

getInorderIndex(int[] preorder, int[] inorder, int begin, int end): int根据前序遍历数组中的根节点，返回根节点在中序遍历数组中的下标；

**思路：**在前序遍历数组中找到二叉树所有子树的根节点，在中序遍历中找到该根节点的下标，下标左边是左树，右边是右树；

    private int preIndex;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = inorder.length;
        preIndex = 0;

        return createTreeByPreorderAndInorder(preorder, inorder, 0, n - 1);
    }

    private TreeNode createTreeByPreorderAndInorder(int[] preorder, int[] inorder, int begin, int end){
        if(begin > end) return null;

        TreeNode root = new TreeNode(preorder[preIndex]);

        int inorderIndex = getInorderIndex(preorder, inorder, begin, end);

        if(inorderIndex == -1) return null;

        preIndex++;

        root.left = createTreeByPreorderAndInorder(preorder, inorder, begin, inorderIndex - 1);

        root.right = createTreeByPreorderAndInorder(preorder, inorder, inorderIndex + 1, end);

        return root;
    }

    private int getInorderIndex(int[] preorder, int[] inorder, int begin, int end){
        for(int i = begin; i <= end; i++){
            if(preorder[preIndex] == inorder[i]){
                return i;
            }
        }
        return -1; 
    }

9. 根据中序遍历和后续遍历构建二叉树

buildTree(int[] inorder, int[] postorder): TreeNode 根据中序遍历和后续遍历创建二叉树；

buildTreeByPostorderAndInorder(int[] postorder, int[] inorder, int begin, int end): TreeNode 根据后序遍历数组，在中序遍历数组中找根节点的下标，并创建根节点和右孩子和左孩子；

findInorderIndex(int[] postorder, int[] inorder, int begin, int end): int根据后序遍历数组中的根节点，返回根节点在中序遍历数组中的下标；

    public int postIndex;

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int n = inorder.length;
        postIndex = n - 1;

        return buildTreeByPostorderAndInorder(postorder, inorder, 0, n - 1);
    }

    public TreeNode buildTreeByPostorderAndInorder(int[] postorder, int[] inorder, int begin, int end){
        if(begin > end) return null;

        TreeNode root = new TreeNode(postorder[postIndex]);

        int inorderIndex = findInorderIndex(postorder, inorder, begin, end);
        if(inorderIndex == -1) return null;

        postIndex--;

        root.right = buildTreeByPostorderAndInorder(postorder, inorder, inorderIndex + 1, end);

        root.left = buildTreeByPostorderAndInorder(postorder, inorder, begin, inorderIndex - 1);

        return root;
    }

    public int findInorderIndex(int[] postorder, int[] inorder, int begin, int end){
        for(int i = begin; i <= end; i++){
            if(inorder[i] == postorder[postIndex]){
                return i;
            }
        }
        return -1;
    }

10. 根据二叉树创建字符串

示例 1：

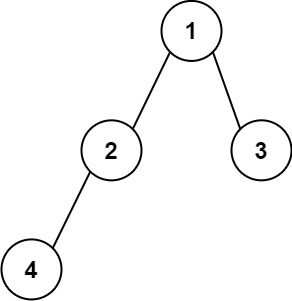
输入： root = [1,2,3,4]
输出： "1(2(4))(3)"
**解释：**初步转化后得到 "1(2(4)())(3()())" ，但省略所有不必要的空括号对后，字符串应该是"1(2(4))(3)" 。

示例 2：

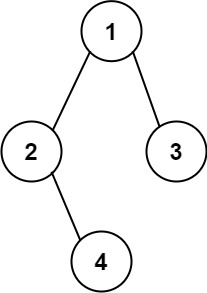
输入： root = [1,2,3,null,4]
输出： "1(2()(4))(3)"
**解释：**和第一个示例类似，但是无法省略第一个空括号对，否则会破坏输入与输出一一映射的关系。

    public StringBuilder ret;
    public String tree2str(TreeNode root) {
        ret = new StringBuilder();
        preorder(root);
        return ret.toString();
    }
    public TreeNode preorder(TreeNode root){
        if(root == null) return null;
        ret.append(root.val);
        if(root.left != null || root.right != null){
            ret.append("(");
            TreeNode left = preorder(root.left);
            ret.append(")");
        }
        if(root.right != null){
            ret.append("(");
            TreeNode right = preorder(root.right);
            ret.append(")");
        }
        return root;
    }

11. 二叉树的非递归遍历

重点：栈可以将递归转化为循环；

前序遍历：

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
            if(cur != null){
                ret.add(cur.val);
                stack.push(cur);
                cur = cur.left;
            }else{
                TreeNode top = stack.pop();
                cur = top.right;
            }
        }
        return ret;
    }

中序遍历：

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
            if(cur != null){
                stack.push(cur);
                cur = cur.left;
            }else{
                TreeNode top = stack.pop();
                ret.add(top.val);
                cur = top.right;
            }
        }
        return ret;
    }

后续遍历：

**思路：**需要加一个 prev 指针，用于标记收集过的节点，如果收集过了，弹出栈的下一个元素即可；

    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;

        while(cur != null || !stack.isEmpty()){
            if(cur != null){
                stack.push(cur);
                cur = cur.left;
            }else{
                TreeNode top = stack.peek();
                if(top.right == null || top.right == prev){
                    top = stack.pop();
                    ret.add(top.val);
                    prev = top;
                }else{
                    cur = top.right;
                }
            }
        }
        return ret;
    }