目录
[2 拉普拉斯展开式](#2 拉普拉斯展开式)
[3 范德蒙德行列式](#3 范德蒙德行列式)
对于行列式的计算来说,一般给出的行列式我们都要对其进行化简,但是化简到什么程度就可以了呢?
这就是本篇的用处,一般给出的行列式化简的目标就是我们接下来这3种。就是说在出题的时候大部分都是按照这3中的一种去出题的,所以我们在化简的时候也要尽量往这4种行列式身上去化简。
1.主(副)对角线行列式

首先是主对角线行列式,这个行列式的特征是主对角上面(或者下面)全为0 。这种行列式的值等于主对角线元素之积。
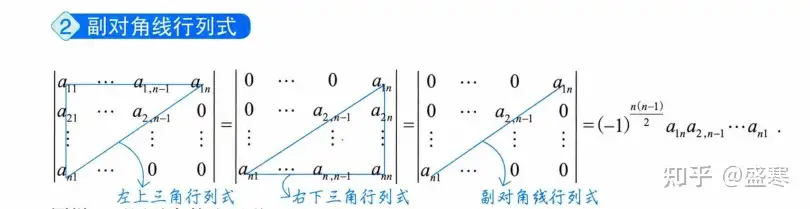
接下来是副对角行列式,特征是副对角线上面(或者下面)全为0 。此行列式可以通过交换转换为主对角行列式,交换的次数为(n-1)n/2,因此要乘以-1的(n-1)n/2次方。
2 拉普拉斯展开式

本展开式的特征是有一块"区域"全为0,大家在解题的时看到有一块区域全为0要想到此展开式。
3 范德蒙德行列式

非常有特色的行列式,我们在看到平方和3次方的时候就想到化简为这种行列式,一般这种行列式化简有两种思路,一种是往上化简,比如有平方和1,你想办法构造出3次方,但是更常用的是把第一行化简为1,这样只需平方和1次方即可。
这个行列式的值就是第2行中后一项减去前一项的所有项的乘积。比如三阶的就是3减1和3减2(因为3前面是1和2),还有2减1(2前面是1,1前面没了)。