文章An Extrinsic Calibration Method between LiDAR and GNSS/INS for Autonomous Driving,https://arxiv.org/pdf/2209.07694 ,
代码 https://github.com/OpenCalib/LiDAR2INS
讲述的是lidar和gnss/ins之间的标定,当然作者用的是几何的方法来进行标定。
首先是问题陈述
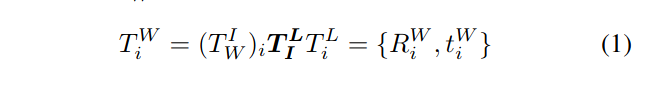
1.生成全局坐标系的点云就通过这个变换来生成,TiL就是计算出来点在雷达坐标系中的坐标;
2.TIL就是雷达坐标系到INS的两者之间的相对变换参数,这个参数就是本篇文章所要求解的参数;3.还有一个参数就是TWI,就是把激光雷达点变换到INS当前坐标系后,还需要根据INS自身的位置和姿态,求解激光雷达点在世界坐标系下的位置。
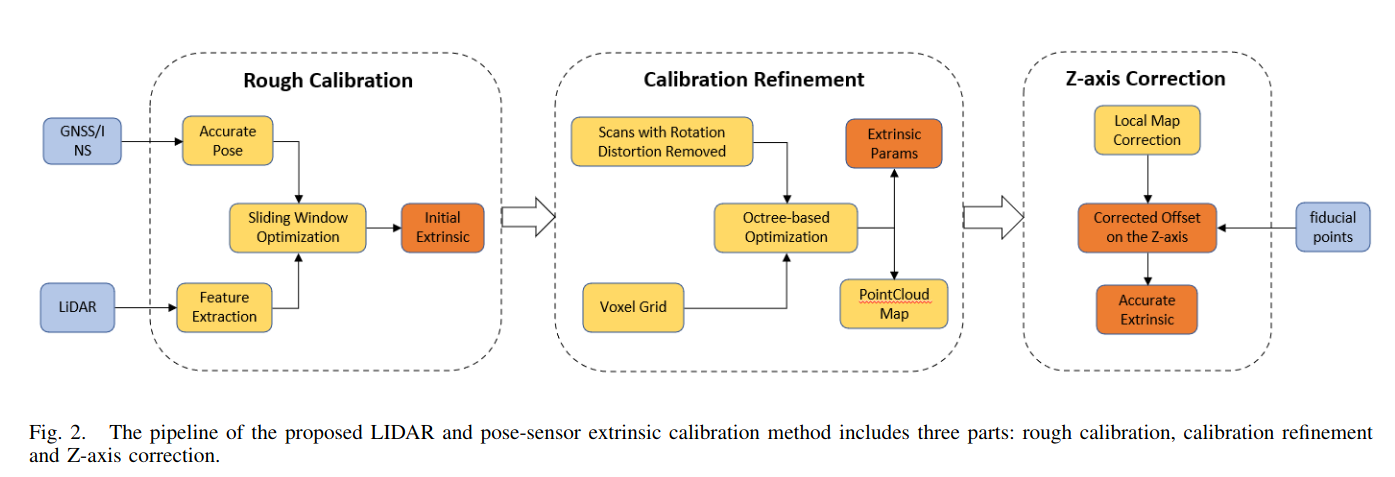
该文章把标定分为了三个部分、分别是粗略的标定、标定优化和z轴矫正。
一、粗略的标定(使用滑动窗口内点到面距离最小来进行的标定)

作者用的滑动窗口,所以就是把1-n帧数据变换到第一帧所在的坐标系下。然后使用BALM中的王个划分方法,也就是八叉树划分方法,把点云划分到体素中,在每一个体素中进行平面拟合,然后在优化的时候就是直接优化的点到平面的距离最小。当然,在优化的过程中是没有优化平面参数的,只优化旋转和平移。
点到平面的距离可以表示为:

可以这样去想象,如果lidar和ins之间的相对位姿特别准,那么如果激光雷达扫描了一个平面,那么所生成的点云应该就基本上上在一个平面上,所以可以用平面这种结构来进行数据的约束和参数的优化。
现在看代码:
在每一个具有平面的体素内构建ceres优化程序。
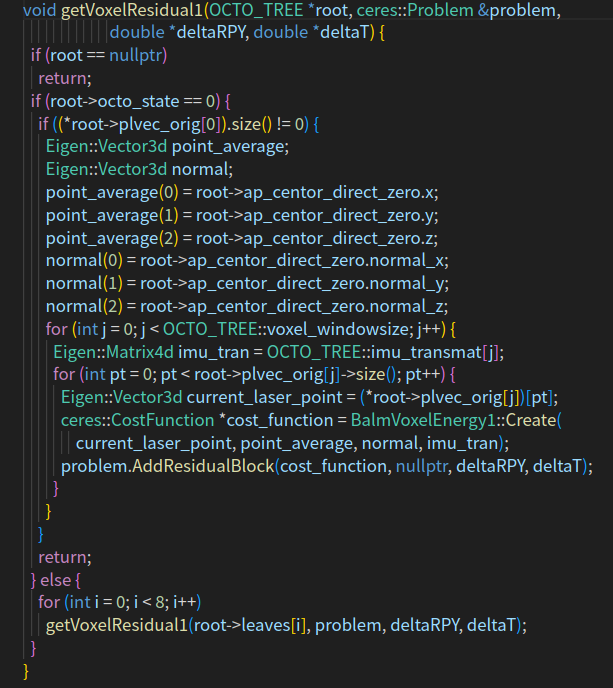
可以看优化函数,就是首先把激光雷达点变换到ins坐标系下,然后在根据从ins获取的旋转和位置,变换到世界坐标系下,然后使用点到面的距离进行优化。
struct BalmVoxelEnergy1 {
BalmVoxelEnergy1(const Eigen::Vector3d ¤t_laser_point,
const Eigen::Vector3d &point_average,
const Eigen::Vector3d &normal,
const Eigen::Matrix4d &imu_tran)
: current_laser_point_(current_laser_point),
point_average_(point_average), normal_(normal), imu_tran_(imu_tran) {}
~BalmVoxelEnergy1() {}
template <typename T>
bool operator()(const T *const q, const T *const t, T *residual) const {
T cur_p[3];
cur_p[0] = T(current_laser_point_(0)); //当前激光点
cur_p[1] = T(current_laser_point_(1));
cur_p[2] = T(current_laser_point_(2));
T world_p[3];
ceres::QuaternionRotatePoint(q, cur_p, world_p); //变换到ins坐标系下
// ceres::AngleAxisRotatePoint(q, cur_p, world_p);
world_p[0] += t[0];
world_p[1] += t[1];
// world_p[2] += t[2];
T tran_p[3];
// n * (p - p_aver) 再变换到世界坐标系下
tran_p[0] = imu_tran_(0, 0) * world_p[0] + imu_tran_(0, 1) * world_p[1] +
imu_tran_(0, 2) * world_p[2] + imu_tran_(0, 3) -
point_average_[0];
tran_p[1] = imu_tran_(1, 0) * world_p[0] + imu_tran_(1, 1) * world_p[1] +
imu_tran_(1, 2) * world_p[2] + imu_tran_(1, 3) -
point_average_[1];
tran_p[2] = imu_tran_(2, 0) * world_p[0] + imu_tran_(2, 1) * world_p[1] +
imu_tran_(2, 2) * world_p[2] + imu_tran_(2, 3) -
point_average_[2];
residual[0] = normal_[0] * tran_p[0] + normal_[1] * tran_p[1] +
normal_[2] * tran_p[2];
return true;
}
static ceres::CostFunction *Create(const Eigen::Vector3d ¤t_laser_point,
const Eigen::Vector3d &point_average,
const Eigen::Vector3d &normal,
const Eigen::Matrix4d &imu_tran) {
auto cost_function =
new ceres::AutoDiffCostFunction<BalmVoxelEnergy1, 1, 4, 3>(
new BalmVoxelEnergy1(current_laser_point, point_average, normal,
imu_tran));
return cost_function;
}
const Eigen::Vector3d current_laser_point_;
const Eigen::Vector3d point_average_;
const Eigen::Vector3d normal_;
const Eigen::Matrix4d imu_tran_;
};二、标定优化(使用占据体素数量最小来进行的标定)
体素占据最小来标定,这个比较好理解,因为参数越精确,分层现象越不可能,所以使用体素占据来优化参数。具体看论文描述。
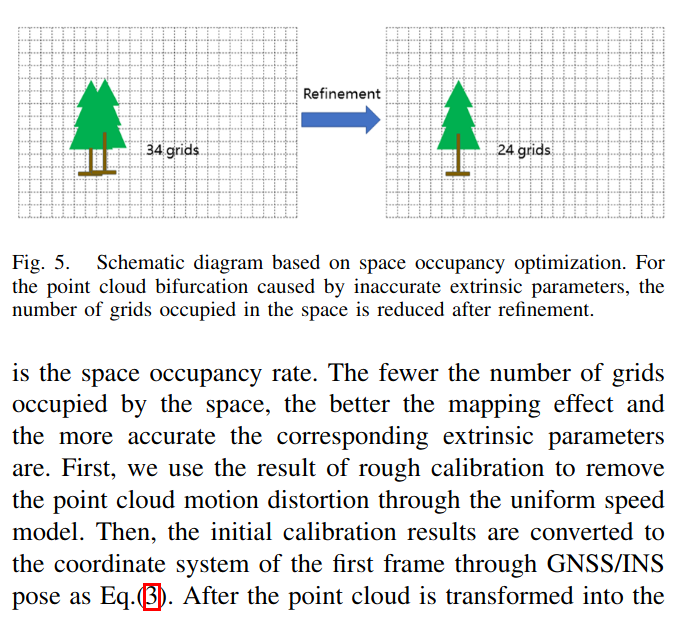
接着看代码是怎么实现体素占据的,实际上不是构建的优化函数来优化的,实际上相对于是不断的尝试试出来的,这里面的iter*direction[j]和xyz_resolution和rpy_resolution是一些参数,这些参数构成了一个deta_transform,附加在粗参数基础上,然后一个参数一个参数的去实验,看看哪一个参数可以减少体素占用数量。最后,就把它作为最优参数。
ar[2] = iter * direction[j] * rpy_resolution;
std::cout << varName[2] << ": " << var[2] << std::endl;
size_t cnt = ComputeVoxelOccupancy(var);
if (cnt < min_voxel_occupancy * (1 - 1e-4)) {
min_voxel_occupancy = cnt;
bestVal[2] = var[2];
std::cout << "points decrease to: " << min_voxel_occupancy << std::endl;
} else {
std::cout << "points increase to: " << cnt << std::endl;
break;
}
}
}
var[2] = bestVal[2];
// tx
for (int j = 0; j <= 1; j++) {
for (int iter = 1; iter < max_iteration; iter++) {
var[3] = iter * direction[j] * xyz_resolution;
std::cout << varName[3] << ": " << var[3] << std::endl;
size_t cnt = ComputeVoxelOccupancy(var);
if (cnt < min_voxel_occupancy * (1 - 1e-4)) {
min_voxel_occupancy = cnt;
bestVal[3] = var[3];
std::cout << "points decrease to: " << min_voxel_occupancy << std::endl;
} else {
std::cout << "points increase to: " << cnt << std::endl;
break;
}
}
}
var[3] = bestVal[3];
// ty
for (int j = 0; j <= 1; j++) {
for (int iter = 1; iter < max_iteration; iter++) {
var[4] = iter * direction[j] * xyz_resolution;
std::cout << varName[4] << ": " << var[4] << std::endl;
size_t cnt = ComputeVoxelOccupancy(var);
if (cnt < min_voxel_occupancy * (1 - 1e-4)) {
min_voxel_occupancy = cnt;
bestVal[4] = var[4];
std::cout << "points decrease to: " << min_voxel_occupancy << std::endl;
} else {
std::cout << "points increase to: " << cnt << std::endl;
break;
}
}
}
var[4] = bestVal[4];
for (size_t i = 0; i < 6; i++) {
curr_best_extrinsic_[i] = bestVal[i];
}
std::cout << "roll: " << bestVal[0] << ", pitch: " << bestVal[1]
<< ", yaw: " << bestVal[2] << ", tx: " << bestVal[3]
<< ", ty: " << bestVal[4] << ", tz: " << bestVal[5] << std::endl;
std::cout << "points: " << min_voxel_occupancy << std::endl;
// calib result
Eigen::Matrix4d deltaT = TransformUtil::GetDeltaT(bestVal);
transform = lidar2imu_initial_ * deltaT;
transform = transform.inverse().eval();
return true;
}三、z轴矫正(使用基准标志来进行z偏移标定)
这个不知道是否有必要,如果在粗标定中,如果体素中提取的平面不是都平行的,在xyz三个方向上都可以构成有效的约束的话,那么是不是就不用进行第三步了。
这一步骤的论文中的意思看下图:

就是用一些设备比如全站仪和rtk打一些地面点,然后册出来一些标志中心的点坐标,在激光雷达扫描到这些坐标的时候,直接使用这些坐标来矫正z方向的偏移。这一步相对来说高理解,但是感觉也是有点奇怪,如果打一些标志,那么只用来约束z-axis吗?