数据结构——顺序表的相关操作

一、顺序表基础认知​

1.顺序表的定义与特点​

顺序表是数据结构中一种线性存储结构，它将数据元素按照逻辑顺序依次存储在一片连续的物理内存空间中。简单来说，就是用一段地址连续的存储单元依次存放线性表的元素，且元素之间的逻辑关系通过物理位置的相邻关系直接体现。​

其核心特点包括：​

• 物理存储连续：所有元素在内存中占据连续的存储空间，例如第 i 个元素的存储地址可通过首地址和元素大小计算（Loc (ai) = Loc (a0) + i×sizeof (元素类型)）。​

• 元素访问高效：支持随机访问，即通过下标可以直接定位到目标元素，时间复杂度为 O (1)。​

• 容量固定或动态调整：静态顺序表的容量在初始化时确定，动态顺序表则可根据元素数量动态扩容或缩容。​

• 插入删除效率低：若在中间位置插入或删除元素，需要移动大量后续元素以维持连续性，时间复杂度为 O (n)。

2.顺序表与数组的关联和区别​

顺序表与数组密切相关，但二者并非完全等同，具体关联和区别如下：​

关联：​

• 顺序表的底层实现依赖数组：无论是静态还是动态顺序表，都会借助数组作为物理存储载体，利用数组的连续内存特性实现元素的线性排列。​

• 元素访问方式一致：两者都支持通过下标直接访问元素，遵循 "随机访问" 的特性。

区别：

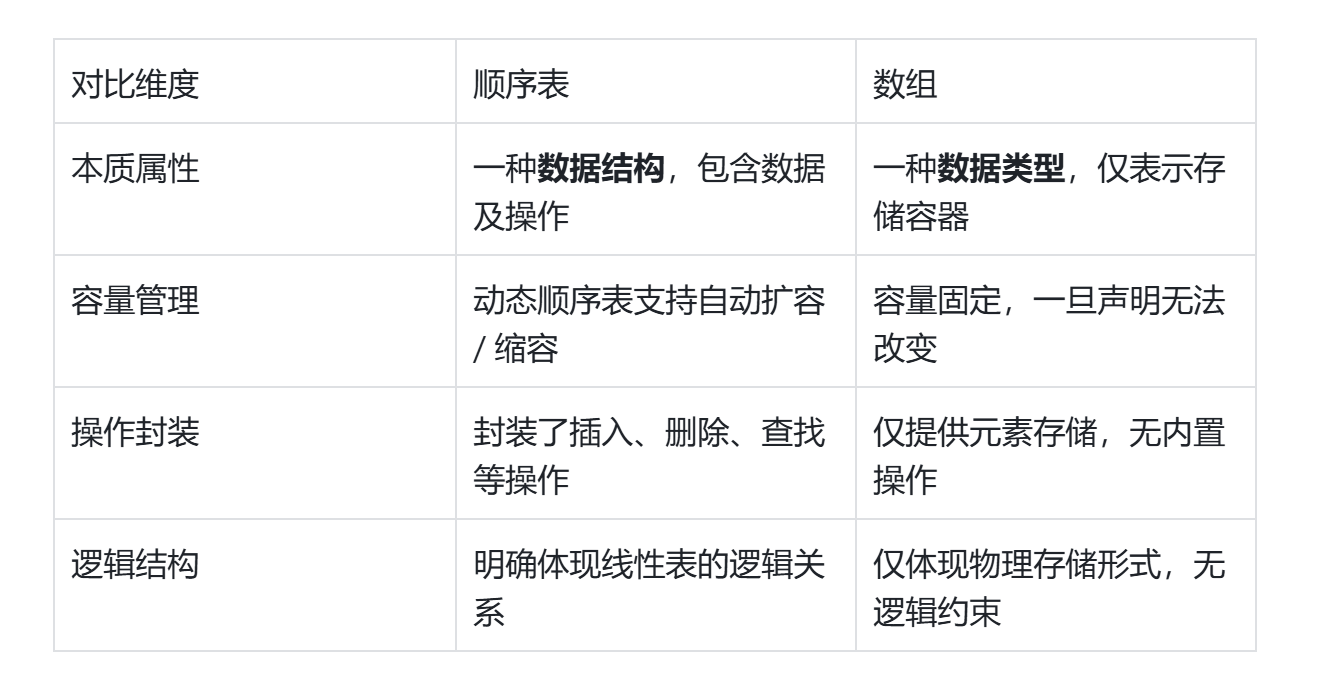
例如，在 C 语言中，数组是int arr[10]这样的固定大小容器，而顺序表则会通过结构体封装数组指针、当前长度和容量，如：​

typedef struct {
    int* data;   // 指向数组的指针
    int size;    // 当前元素个数
    int capacity; // 容量
} SeqList;

二、顺序表的初始化操作​

//1.初始化
void InitSeqList(SeqList* plist)
{
	//断言
	assert(plist != NULL);
	//1.给指针malloc分配内存
	ELEM_TYPE* p = (ELEM_TYPE*)malloc(sizeof(ELEM_TYPE) * SXQ_INIT_SIZE);
	if (NULL == p)
	{
		printf("初始化malooc分配内存失败\n");
		return;
	}
	plist->arr = p;
	//2.个数
	plist->cursize = 0;
	//3.容量
	plist->capacity = SXQ_INIT_SIZE;
}

三、顺序表的核心操作​

1.插入元素（头部、中间、尾部）

//7.插入元素
bool InsertElem(SeqList* plist, int pos, ELEM_TYPE val)
{
	assert(plist != NULL);
	if (IsFull(plist))
	{
		if (IncMem(plist) == false)
		{
			printf("无法插入\n");
			return false;
		}
	}
	if (pos<0 || pos>plist->cursize)
	{
		printf("插入位置不合法\n");
		return false;
	}
	for (int i = plist->cursize - 1; i >= pos; i--)
	{
		plist->arr[i + 1] = plist->arr[i];
	}
	plist->arr[pos] = val;
	plist->cursize += 1;
	return true;
}

//8.尾插
bool Push_Back(SeqList* plist, ELEM_TYPE val)
{
	assert(plist != NULL);
	plist->arr[plist->cursize] = val;
	plist->cursize++;
	return true;
}

//9.头插
bool Push_Front(SeqList* plist, ELEM_TYPE val)
{
	assert(plist != NULL);
	InsertElem(plist, 0, val);
	return true;
}

2.​删除元素（指定位置、指定值）​

//12.按位置删除
bool ErasePos(SeqList* plist, int index)
{
	assert(plist != NULL);
	if (IsEmpty(plist))
	{
		printf("删除失败\n");
		return false;
	}
	if (index<0 || index>plist->cursize)
	{
		printf("删除失败\n");
		return false;
	}
	for (int i = index; i < plist->cursize; i++)
	{
		plist->arr[i] = plist->arr[i + 1];
	}
	plist->cursize -= 1;
	return true;
}

//13.按值删除（删一次）
bool RemoveElem(SeqList* plist, ELEM_TYPE val)
{
	assert(plist != NULL);
	for (int i = 0; i < plist->cursize; i++)
	{
		if (val == plist->arr[i])
		{
			ErasePos(plist, i);
		}
	}
	return true;
}

//14.按值删除（删多次）
bool RemoveElemAll(SeqList* plist, ELEM_TYPE val)
{
	assert(plist != NULL);
	int i = 0;
	while (i < plist->cursize)
	{
		if (plist->arr[i] == val)
		{
			ErasePos(plist, i);
		}
		else
		{
			i++;
		}
	}
	return true;
}

//15.删除尾
bool Pop_Back(SeqList* plist)
{
	assert(plist != NULL);
	if (IsEmpty(plist))
	{
		return false;
	}
	ErasePos(plist, plist->cursize - 1);
	return true;
}

//16.删除头
bool Pop_Front(SeqList* plist)
{
	assert(plist != NULL);
	if (IsEmpty(plist))
	{
		return false;
	}
	ErasePos(plist, 0);
	return true;
}

3.查找元素（按值查找、按位查找）

//11.查询
int FindValue(const SeqList* plist, ELEM_TYPE val)//没找到返回-1，找到了返回下标，有多个返回第一个
{
	assert(plist != NULL);
	if (IsEmpty(plist))
	{
		return -1;
	}
	for (int i = 0; i < plist->cursize; i++)
	{
		if (plist->arr[i] == val)
		{
			printf("找到了，下标为%d\n", i);
			return i;
		}
	}
	return -1;
}

四、顺序表的销毁操作​

//22.清除顺序表
bool ClearElem(SeqList* plist)
{
	assert(plist != NULL);
	plist->cursize = 0;
	return true;
}

//23.销毁
void DestroySeqList(SeqList* plist)
{
	assert(plist != NULL);
	free(plist->arr);
	plist->arr = NULL;
	plist->cursize = 0;
	plist->capacity = 0;
}

五、反转、合并两个有序的顺序表

//24.反转顺序表
void Reverse_List(SeqList* plist)
{
	assert(plist != NULL);
	if (IsEmpty(plist))
	{
		return;
	}
	int left = 0;
	int right = plist->cursize - 1;
	while (left < right)
	{
		int temp = plist->arr[left];
		plist->arr[left] = plist->arr[right];
		plist->arr[right] = temp;
		left++;
		right--;
	}
}

//25.合并两个有序的顺序表
void Merge_List(SeqList* plist1, SeqList* plist2, SeqList* plist3)
{
	assert(plist1 != NULL && plist2 != NULL && plist3 != NULL);
	int i = 0, j = 0;
	while (i < plist1->cursize || j < plist2->cursize)
	{
		if (plist1->arr[i] > plist2->arr[j])
		{
			Push_Back(plist3, plist2->arr[j]);
			j++;
		}
		else
		{
			Push_Back(plist3, plist1->arr[i]);
			i++;
		}
		if (i == plist1->cursize)
		{
			while (j < plist2->cursize)
			{
				Push_Back(plist3, plist2->arr[j]);
				j++;
			}
		}
		if (j == plist2->cursize)
		{
			while (i < plist1->cursize)
			{
				Push_Back(plist3, plist1->arr[i]);
				i++;
			}
		}
	}

}