从“最短响应路径”到二叉树最小深度：一个Bug引发的BFS探险之旅（111. 二叉树的最小深度）

🌿 从"最短响应路径"到二叉树最小深度：一个Bug引发的BFS探险之旅 😎

嘿，各位码农朋友们！我是你们的老朋友，一个在代码世界里摸爬滚打了多年的老兵。今天，我想跟你们聊聊一个我最近在项目中遇到的"小麻烦"，以及我是如何从一个看似简单的需求，一步步深入到数据结构的核心，并最终找到最优解的。这趟旅程不仅解决了一个棘手的Bug，还让我对二叉树的最小深度有了全新的认识。😉

我遇到了什么问题？

想象一下这个场景：我正在为一个大型电商平台开发一套实时的服务监控系统。我们的后端架构是微服务化的，用户的一个简单操作，比如"下单"，可能会触发一系列的服务调用。例如，订单服务调用库存服务，库存服务又调用物流服务...... 这形成了一个复杂的调用链，就像一棵树。

我的任务是，为这个调用链添加一个"健康度"指标：计算完成一次请求所经过的"最短"成功路径。这里的"路径"指的是调用的服务数量，"成功"路径的终点是一个"终端服务"（Leaf Node），也就是它不再依赖任何其他服务。

为啥要这个指标？因为它可以帮我们评估系统最理想的响应性能，如果连最短路径的耗时都超标了，那整个系统肯定出问题了！🚀

起初我心想，这不就是找一棵树里，从根节点到最近叶子节点的距离嘛？简单！然后，我就愉快地掉进了第一个坑里。😅

我是如何用算法解决的

这个问题，其实就是大名鼎鼎的 LeetCode 算法题：

111. 二叉树的最小深度

题目描述： 给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明： 叶子节点是指没有子节点的节点。

提示解读

树中节点数的范围在 [0, 10^5] 内：这个提示非常关键！它告诉我，节点数量可能很大，我的算法必须足够高效，通常需要是线性时间复杂度 O(N) 才能通过。暴力或者低效的 O(N^2) 算法肯定会超时。

-1000 <= Node.val <= 1000：节点的值对我们解决这个问题没有影响，它只是树结构的一部分。我们可以忽略这个值的具体含义。

第一次尝试：深度优先搜索（DFS）的"陷阱"

我首先想到的就是递归，写起来又快又优雅，这不就是深度优先搜索（DFS）的拿手好戏嘛？于是我很快写出了第一版代码：

java 复制代码

// 错误示范！！！这是一个大坑！
public int minDepth_wrong(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // 想当然地认为最小深度就是左右子树最小深度里更小的那个+1
    return 1 + Math.min(minDepth_wrong(root.left), minDepth_wrong(root.right));
}

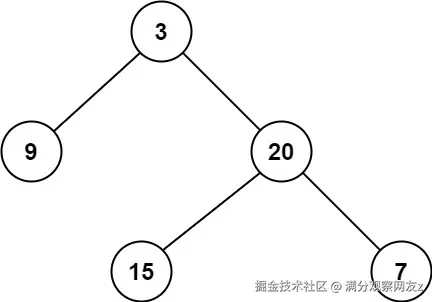
我用 [3,9,20,null,null,15,7] 这个例子一测，结果是2，完美！正当我准备提交代码时，一个测试用例让我傻眼了：[2,null,3,null,4,null,5,null,6]。

我的代码输出是 1，但正确答案是 5！🤯

问题出在哪？minDepth_wrong(Node(2)) 会计算 1 + min(minDepth_wrong(null), minDepth_wrong(Node(3)))。minDepth_wrong(null) 返回 0，于是结果就成了 1 + min(0, 4) = 1。

恍然大悟的瞬间 😉： 我完全搞错了"最小深度"的定义！题目要求的是到叶子节点 的最小深度。对于节点2，它只有一个右子树，它不是叶子节点，所以它的深度不能是1。我们必须沿着它唯一的子树走下去，直到找到一个真正的叶子节点（Node(6)）！

所以，正确的 DFS 逻辑应该是：

如果一个节点，左子树为空，那它的最小深度只能由右子树决定。
同理，如果右子树为空，那最小深度只能由左子树决定。
只有当左右子树都存在时，我们才取其中较小的那个。

于是，我修复了我的 DFS 代码：

修正后的深度优先搜索 (DFS) - 递归解法

java 复制代码

/*
 * 思路：递归计算每个节点的最小深度。
 * 关键点在于正确处理只有一个子节点的情况。
 * 时间复杂度：O(N)，因为每个节点都要访问一次。
 * 空间复杂度：O(H)，H是树的高度，用于递归调用栈。最坏情况是O(N)。
*/
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
      
        // 递归获取左右子树的最小深度
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
      
        // ✨ 这里是核心逻辑！ ✨
        // 如果一个子树为空（例如 leftDepth == 0），
        // 那么我们必须走另一条路。此时，当前节点的最小深度是 非空子树深度 + 1。
        // Math.max(leftDepth, rightDepth) 在一个为0时，会巧妙地选择另一个非0的深度。
        if (root.left == null || root.right == null) {
            return 1 + Math.max(leftDepth, rightDepth);
        }
      
        // 如果左右子树都存在，我们才选择更短的那条路径。
        // 使用 Math.min API 来获取两个数中较小的那个。
        return 1 + Math.min(leftDepth, rightDepth);
    }
}

这下总算对了！但转念一想，DFS 为了找到最小深度，可能会一头扎进一个很深的路径里，直到走完才回头。有没有更直接的方法呢？这让我思考起了另一种经典的遍历方式。

更优解：广度优先搜索（BFS）的"降维打击"

"恍然大悟"的又一个瞬间💡： 我要求的是"最短路径"，这不就是广度优先搜索（BFS）的经典应用场景吗！BFS 就像往水里扔一块石头，水波会一圈一圈地向外扩散。它逐层遍历树的节点，所以，它遇到的第一个叶子节点，必然位于最浅的层，其深度就是我们要求的最小深度！一旦找到，搜索就可以立即停止，效率简直爆表！

广度优先搜索 (BFS) - 迭代解法

java 复制代码

/*
 * 思路：利用队列实现层序遍历。
 * BFS的特性保证了我们找到的第一个叶子节点，一定是深度最小的。
 * 时间复杂度：O(N)，最坏情况访问所有节点。
 * 空间复杂度：O(W)，W是树的最大宽度，用于队列存储。
*/
import java.util.Queue;
import java.util.LinkedList;

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        // Java中我们常用 Queue 接口，并选择 LinkedList 或 ArrayDeque 作为实现。
        // LinkedList 是一个双向链表，提供了队列操作（offer/poll）。
        // ArrayDeque 基于循环数组，通常在作为队列或栈使用时性能更优。这里两者皆可。
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 1;

        while (!queue.isEmpty()) {
            int levelSize = queue.size(); // 关键一步：确定当前层的节点数
            for (int i = 0; i < levelSize; i++) {
                TreeNode currentNode = queue.poll();

                // ✅ 检查是否是叶子节点
                if (currentNode.left == null && currentNode.right == null) {
                    return depth; // 找到第一个，立即返回！
                }

                if (currentNode.left != null) {
                    queue.offer(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.offer(currentNode.right);
                }
            }
            depth++; // 进入下一层
        }
        return depth; // 理论上不会执行到这里
    }
}

我们用 [3,9,20,null,null,15,7] 这个例子来走一遍 BFS 的流程：

depth=1 : 队列里有 [3]。3不是叶子节点，把它弹出，把 9 和 20 加进去。
depth=2 : 队列里有 [9, 20]。先处理 9，发现它是叶子节点！立刻返回 depth，也就是 2。 后面的 20 及其子节点根本不需要再看了。

这就是 BFS 的威力！它天生就是为解决最短路径问题而生的。在我的监控系统项目中，这意味着我们能以最快的速度找到那个理想的"最短响应路径"，而不用浪费时间去探索那些又长又复杂的调用链。

举一反三，触类旁通

掌握了"最小深度"的求解方法后，你会发现这个思想能用在很多地方：

社交网络：计算两个人之间的"最小关系链"（比如 LinkedIn 的一度、二度人脉）。
网络路由：在路由器网络中找到从A点到B点的最少跳数（Hop）。
游戏开发：在迷宫中寻找从起点到终点的最短路径。

所有这些"最短"问题，BFS 都是你的首选利器！

练练手吧！

光说不练假把式。如果你想巩固这个知识点，我强烈推荐你去 LeetCode 上刷刷下面这几道相关的题目，它们能让你对树的遍历有更深的理解：

104. 二叉树的最大深度: 最小深度的"孪生兄弟"，练习 DFS 的好题目。
102. 二叉树的层序遍历: 练习 BFS 的基础和核心。
559. N 叉树的最大深度: 把二叉树的概念扩展到多叉树。
1162. 地图分析 (原题名：地图分析)：一个更复杂的、在网格上应用多源 BFS 的绝佳例子。

希望我的这次"踩坑"和"顿悟"之旅能对你有所启发。编程的世界就是这样，问题背后往往隐藏着优美的数据结构和算法思想。下次当你再遇到"最短"、"最快"、"最少"这类问题时，希望你能自信地喊出："上 BFS！" 😎

下次见！继续愉快地 coding 吧！