2.1什么是向量
线性代数里主要是对向量进行计算,但在学习向量之前,首先对标量进行定义。
2.1.1 标量
标量(Scalar)是一个单一的数值,比如你的年龄,你的体重都是一个标量值。
2.1.2 向量的定义
接下来我们来讨论向量。不同背景的人可能对向量的理解不同。 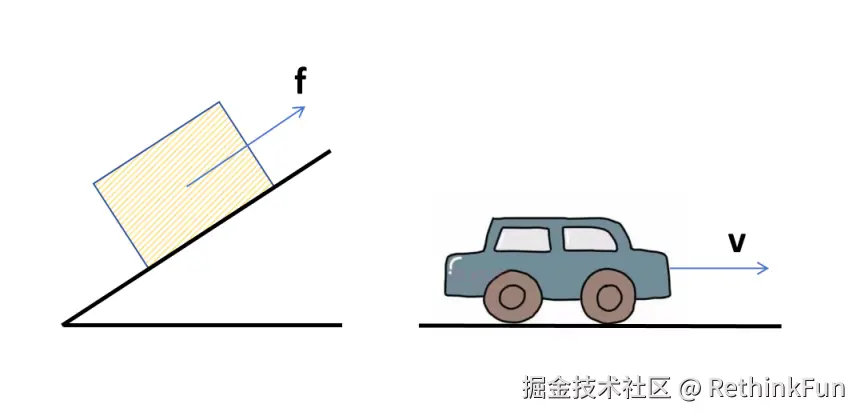
物理里的向量 物理里的向量用带箭头的线段来表示。确切的说它是一个自由向量,它只关心向量的大小和方向,而对这个向量在空间里的位置不关心。可以用这个向量表示力,速度这样既有大小又有方向的物理量。其中线段的长度表示这个物理量的大小,箭头的方向表示物理量的方向。因为物理研究的是现实世界,它的向量只存在于二维或者三维空间里。
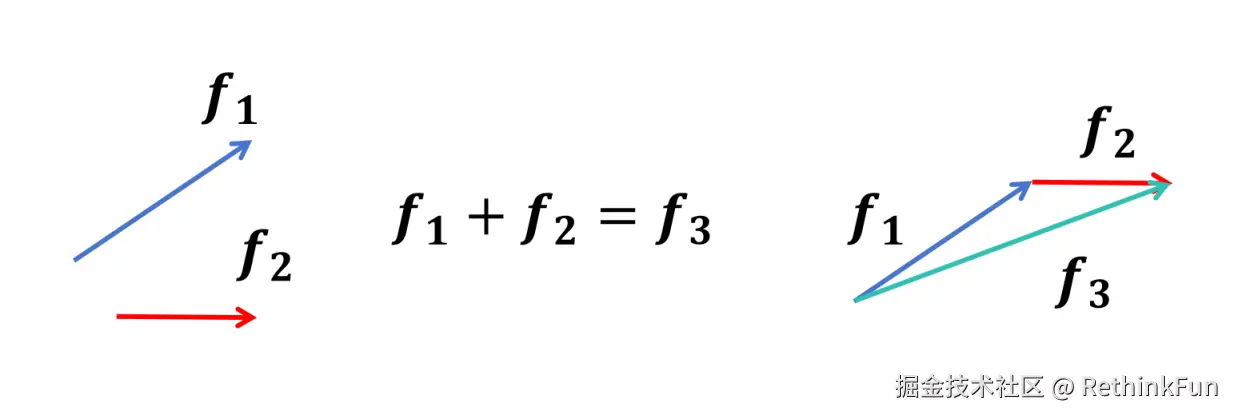
并且我们知道,在物理里的向量是可以进行加减法和数乘的。
比如作用在同一点上的两个力可以组成合力,可以用三角形法则进行计算。也就是将向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 1 f_1 </math>f1和向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 2 f_2 </math>f2首尾相连,在从 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 1 f_1 </math>f1的尾连接到 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 2 f_2 </math>f2的首构成的向量,就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 1 f_1 </math>f1和 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 2 f_2 </math>f2两个向量的和。物理里也可以对向量进行数乘,表示对向量进行缩放,比如对一个速度乘以0.4,表示速度大小为原来的0.4倍,但是方向不变。
机器学习里的向量 机器学习里的向量表示一组有序的数。比如你收集学生们的年龄,身高,体重。那么收集时这3个数字排列顺序是至关重要的。 比如你收集了两个同学的数据。然后你想计算这两个人的平均年龄,平均身高和平均体重。
<math xmlns="http://www.w3.org/1998/Math/MathML"> x = [ 12 175 60 ] y = [ 13 145 50 ] \mathbf{x} =\begin{bmatrix}12 \\175 \\60\end{bmatrix}\mathbf{y} =\begin{bmatrix}13 \\145 \\50\end{bmatrix} </math>x= 1217560 y= 1314550
那么你首先把这两个向量对应位置的值相加。
<math xmlns="http://www.w3.org/1998/Math/MathML"> x + y = [ 12 + 13 175 + 145 60 + 50 ] = [ 25 320 110 ] \mathbf{x+y} =\begin{bmatrix}12+13 \\175+145 \\60+50\end{bmatrix}=\begin{bmatrix}25 \\320 \\110\end{bmatrix} </math>x+y= 12+13175+14560+50 = 25320110
然后对求和后向量里的每个值乘以0.5。
<math xmlns="http://www.w3.org/1998/Math/MathML"> m e a n = 0.5 × [ 25 320 110 ] = [ 0.5 × 25 0.5 × 320 0.5 × 110 ] = [ 12.5 160 55 ] \mathbf{mean} =0.5\times\begin{bmatrix}25 \\320 \\110\end{bmatrix} =\begin{bmatrix}0.5\times25 \\0.5\times320 \\0.5\times110\end{bmatrix}=\begin{bmatrix}12.5 \\160\\55\end{bmatrix} </math>mean=0.5× 25320110 = 0.5×250.5×3200.5×110 = 12.516055
最后得到的向量就表示这两个同学的平均年龄,身高,和体重。也是对这个向量进行加法和数乘的计算。
线性代数里的向量
线性代数对向量进行了抽象定义,向量(Vector)是由 n 个标量组成的有序数列。其中这些标量值称为向量的元素或者分量。第 i 个标量称为向量的第 i 个分量。n 称为这个向量的维度。这个 n 维向量可以排成一行,也可以排成一列,分别称为行向量和列向量。一般在线性代数里习惯用列向量。比如上边收集到的学生年龄,身高,体重的数据,可以如下表示:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x = [ 12 175 60 ] \mathbf{x} =\begin{bmatrix}12 \\175 \\60\end{bmatrix} </math>x= 1217560
在本书里向量用小写粗体来表示。上边的x就是一个3维列向量。第一个分量表示年龄,第二个分量表示身高,第三个分量表示体重。
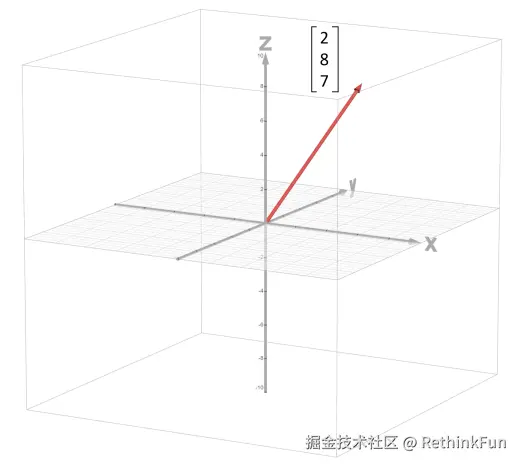
线性代数中的向量,必须存在于一个坐标系内,也叫做向量空间。用一个箭头表示,起点必须在原点,箭头的坐标是一组有序的数,就代表这个向量。
向量的长度,叫做向量的模。对于向量v的模,用下边符号表示。
<math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ v ∣ \left | v \right | </math>∣v∣
假如向量v 由n个分量构成 <math xmlns="http://www.w3.org/1998/Math/MathML"> v 1 , v 2 , . . . v n v_1,v_2,...v_n </math>v1,v2,...vn,则:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ v ∣ = v 1 2 + v 2 2 + . . . + v n 2 2 \left | v \right | =\sqrt[2]{v_1^{2}+v_2^{2}+...+v_n^{2} } </math>∣v∣=2v12+v22+...+vn2
2.1.2 向量的计算
线性代数里主要研究向量间的加法和数乘运算。
两个向量相等的比较
只有两个向量它们每个分量的值都相等时,这两个向量才相等。以上边表示年龄,身高,体重的向量为例,也就是说只有两个人的年龄相等,身高相等,体重相等,才说这两个向量是相等的。因为只有对应维度的数据比较才有意义。
两个向量的相加
<math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 = [ 12 175 60 ] x 2 = [ 11 160 50 ] \mathbf{x_1} =\begin{bmatrix}12 \\175 \\60\end{bmatrix}\mathbf{x_2} =\begin{bmatrix}11 \\160 \\50\end{bmatrix} </math>x1= 1217560 x2= 1116050
<math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 + x 2 = [ 12 175 60 ] + [ 11 160 50 ] = [ 23 335 110 ] \mathbf{x_1+x_2} =\begin{bmatrix}12 \\175 \\60\end{bmatrix}+\begin{bmatrix}11 \\160 \\50\end{bmatrix}=\begin{bmatrix}23 \\335 \\110\end{bmatrix} </math>x1+x2= 1217560 + 1116050 = 23335110
对两个向量进行的另一个常见操作是相加,两个向量相加,是对应分量进行相加。比如你收集了两个同学的年龄,身高,体重信息,组成了两个向量,你要把这两个向量进行加和,则他们的年龄和年龄,身高和身高,体重和体重分别相加。最终的结果表示两个同学年龄的和,身高的和,体重的和。
这里向量加法和物理中向量加法并不冲突,也可以根据三角形法则进行计算。
向量的数乘 向量的数乘,表示对向量的缩放,缩放的英语单词为scaling,标量的英语是scalar。在向量运算里标量的作用就是对向量进行缩放。数乘对向量的缩放是通过对向量的每个分量进行缩放进行的。特别的是,如果缩放的标量为负值,则缩放后的向量与原向量的方向相反。
向量的减法 有了向量的加法和数乘定义,自然就有了向量的减法。向量a 减去向量b ,可以让b 缩放-1,然后a 与缩放-1倍的b相加。
这个教程我也会同步在B站以视频教程的形式更新,欢迎大家在B站关注RethinkFun