探索VB.NET中的贝塞尔Bezier曲线绘制技巧

简介：Bezier曲线是计算机图形学中用于创建平滑曲线的重要工具，广泛应用于图形设计、游戏开发、CAD系统等领域。本文深入探讨了Bezier曲线的基础知识，并详细说明了如何在Visual Basic中使用 Graphics 对象的 DrawBezier 方法绘制曲线。通过理论学习和实践操作，读者将掌握调整控制点以实现曲线平滑的技巧，增强在图形编程方面的能力。

1. Bezier曲线概念与应用

在现代计算机图形学中，Bezier曲线作为一项基础且强大的工具，在各个领域中扮演着极其重要的角色。不论是网页设计、图形设计、游戏开发还是CAD系统，Bezier曲线都以其实现路径平滑、形状编辑简便的特点获得了广泛的应用。简单来说，Bezier曲线是一种通过控制点来定义路径的数学模型。通过增加控制点的数量和位置，我们可以创建从直线到复杂曲线的各种图形。在下一章节中，我们将深入探索Bezier曲线的数学原理，以及如何在实际应用中利用这些原理来实现更加丰富的视觉效果。

2. Bezier曲线的数学原理

2.1 Bezier曲线的定义和特性

2.1.1 Bezier曲线的几何解释

Bezier曲线是一种参数曲线，它通过一组称为"控制点"的点来定义。这条曲线最显著的特性之一是它不一定会穿过每一个控制点，而是由这些点来"引导"曲线的形状。在几何解释上，可以将Bezier曲线看作是控制点定义的多边形边缘的"平滑化"。

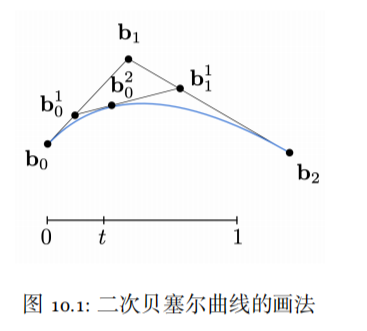
让我们来看一个二次Bezier曲线的例子。一个二次Bezier曲线由三个控制点定义：

• P0（起点）
• P1（控制点）
• P2（终点）

这个二次Bezier曲线可以被解释为P0和P2之间的线段按照P1的位置进行弯曲的结果。随着参数t从0变化到1，曲线上的点依次通过点P0、P1和P2，定义了一个平滑的过渡路径。通过调整P1的位置，可以控制曲线的弯曲程度和方向。

2.1.2 Bezier曲线的代数形式

从代数的角度来说，Bezier曲线可以用基函数和控制点坐标来表达。对于二次Bezier曲线，其数学表达式如下：

B(t) = (1 - t)\^2 \\cdot P0 + 2 \\cdot (1 - t) \\cdot t \\cdot P1 + t\^2 \\cdot P2

其中，( B(t) ) 表示曲线上在参数t处的点，( P0, P1, P2 )是控制点坐标，t是参数，取值范围在[0, 1]之间。这个公式可以用来计算曲线上任何点的位置。

在实际应用中，参数t常常被看作是时间或者迭代步长，使得我们可以沿着曲线插值计算出一系列的点，这些点可以用来绘制整个曲线的形状。

2.2 Bezier曲线的数学基础

2.2.1 参数方程和向量表示

Bezier曲线的参数方程使用向量形式表示，这种表示方式使得计算更为直观和方便。例如，一个三次Bezier曲线可以用四个控制点( P_0, P_1, P_2, P_3 )和参数( t )定义如下：

B(t) = (1 - t)\^3 \\cdot P_0 + 3 \\cdot (1 - t)\^2 \\cdot t \\cdot P_1 + 3 \\cdot (1 - t) \\cdot t\^2 \\cdot P_2 + t\^3 \\cdot P_3

其中，( t )是一个在区间[0, 1]内的参数，( B(t) )是在参数t时刻曲线上点的向量表示。

2.2.2 控制点和基函数的作用

控制点是定义Bezier曲线形状的关键。每一个控制点都对曲线的形状有影响，而这种影响的大小由基函数决定。基函数，也称为Bernstein多项式，在Bezier曲线的方程中起到了分配参数t所代表的权重的作用。

• 对于二次Bezier曲线，其基函数是( (1 - t)^2, 2 \cdot (1 - t) \cdot t, t^2 )。
• 对于三次Bezier曲线，则是( (1 - t)^3, 3 \cdot (1 - t)^2 \cdot t, 3 \cdot (1 - t) \cdot t^2, t^3 )。

每个基函数随着参数t的变化，在0到1之间变化，这些变化对应了在曲线形状中不同控制点的"权重"。因此，通过调整控制点的位置，我们可以控制曲线在不同区段的弯曲程度。

2.3 Bezier曲线的构建和计算方法

2.3.1 递归细分算法

递归细分算法（也称为De Boor-Cox算法）是一种计算Bezier曲线的常用方法。这个算法的基本思想是将一条Bezier曲线分割成两条新的Bezier曲线，并递归地应用这一过程，直到曲线足够接近直线，或者达到所需的精度。

• 首先，将曲线等分为两部分，找到曲线的中点。
• 然后，将两部分继续细分，直至达到预定的分割深度。
• 在每次分割时，都会生成新的控制点。

这个过程可以用递归函数来实现，递归的基本步骤就是基于当前控制点计算新的控制点，然后对新控制点重复此过程。递归细分算法的伪代码如下：

function DeBoorCox(controlPoints, t, depth)
  if depth < threshold then
    return CalculatePoint(controlPoints, t)
  end if
  // 分割控制点
  newControlPoints = SplitControlPoints(controlPoints)
  // 递归计算左半部分曲线
  leftCurve = DeBoorCox(newControlPoints.left, t, depth - 1)
  // 递归计算右半部分曲线
  rightCurve = DeBoorCox(newControlPoints.right, t, depth - 1)
  // 合并曲线
  return MergeCurves(leftCurve, rightCurve)
end function

2.3.2 De Casteljau算法详解

De Casteljau算法是另一种计算Bezier曲线的数值方法，它具有数值稳定性和几何不变性的优点，特别适合用于计算和绘制复杂度较高的Bezier曲线。算法基于一种称为仿射组合的概念，通过一系列的线性插值操作来计算曲线上的点。

De Casteljau算法的基本步骤如下：

1. 在控制点上，进行线性插值以获得新的点集。
2. 使用新的点集重复上述线性插值过程，直到只剩下一个点。
3. 这个最终得到的点就是参数t对应的Bezier曲线上的一点。

function DeCasteljau(controlPoints, t)
  points = controlPoints
  while length(points) > 1 do
    newPoints = []
    for i = 0 to length(points) - 2 do
      newPoints.append((1 - t) * points[i] + t * points[i + 1])
    end for
    points = newPoints
  end while
  return points[0]
end function

这个算法的一个关键特点是，由于它的计算过程是基于线性插值的，所以可以直观地表示为控制点上的向量操作。De Casteljau算法的几何解释是，通过在控制点之间进行线性插值来逼近曲线，这为理解Bezier曲线提供了直观的几何理解。

3. Visual Basic中DrawBezier方法的使用

Visual Basic（简称VB）作为一种简单易用的编程语言，它提供了一些用于绘制图形和曲线的内置方法，其中 DrawBezier 方法允许用户绘制贝塞尔曲线。本章节将深入探讨如何在Visual Basic中使用 DrawBezier 方法来绘制贝塞尔曲线，包括其基础介绍、高级应用以及优化技巧。

3.1 DrawBezier方法基础介绍

3.1.1 方法的语法结构

DrawBezier 方法是 Graphics 类中的一个成员函数，用于绘制贝塞尔曲线。它接受四个点作为参数，分别为起点、两个控制点以及终点。下面展示的是 DrawBezier 方法的基本语法结构：

Public Sub DrawBezier(ByVal pen As Pen, ByVal pt1 As Point, ByVal pt2 As Point, ByVal pt3 As Point, ByVal pt4 As Point)

AI写代码vb

• pen ：定义曲线颜色、宽度和其他样式属性的 Pen 对象。
• pt1 、 pt2 、 pt3 、 pt4 ：分别是贝塞尔曲线的起点、第一个控制点、第二个控制点和终点。

3.1.2 参数详解和实例演示

在这部分，我们将通过一个实例演示来更深入地理解 DrawBezier 方法的使用。

Private Sub Form1_Paint(sender As Object, e As PaintEventArgs) Handles Me.Paint
    Dim g As Graphics = e.Graphics
    ' 创建一个Pen对象，用于定义绘制的样式
    Dim pen As New Pen(Color.Black, 2)
    ' 定义贝塞尔曲线的起点、两个控制点和终点
    Dim pt1 As New Point(50, 50)
    Dim pt2 As New Point(100, 10)
    Dim pt3 As New Point(200, 190)
    Dim pt4 As New Point(250, 250)
    ' 调用DrawBezier方法绘制贝塞尔曲线
    g.DrawBezier(pen, pt1, pt2, pt3, pt4)
End Sub

在这个示例中，我们创建了一个窗体应用程序，并在窗体的 Paint 事件处理程序中使用 DrawBezier 方法绘制了一条贝塞尔曲线。通过定义四个点，我们可以看到曲线从起点开始，经过第一个控制点和第二个控制点的"拉动"，最终到达终点。

3.2 DrawBezier方法的高级应用

3.2.1 结合图形用户界面的应用

在图形用户界面中， DrawBezier 方法可以用于绘制自定义的图形和动画效果。要结合GUI应用，通常需要将绘图代码放置在特定的事件处理程序中，例如按钮点击事件、定时器事件等。

在以下示例中，我们将创建一个按钮，点击该按钮时，在窗体上绘制一条新的贝塞尔曲线：

Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Button1.Click
    ' 调用绘制贝塞尔曲线的过程
    DrawBezierCurveOnForm()
End Sub
 
Private Sub DrawBezierCurveOnForm()
    Dim g As Graphics = Me.CreateGraphics()
    ' 创建一个蓝色的Pen对象
    Dim pen As New Pen(Color.Blue, 3)
    ' 定义新的贝塞尔曲线的点
    Dim pt1 As New Point(30, 30)
    Dim pt2 As New Point(150, 20)
    Dim pt3 As New Point(220, 200)
    Dim pt4 As New Point(300, 250)
    ' 绘制贝塞尔曲线
    g.DrawBezier(pen, pt1, pt2, pt3, pt4)
    ' 释放资源
    g.Dispose()
End Sub

3.2.2 与其他绘图方法的结合

为了创建更加丰富的视觉效果， DrawBezier 方法可以与其他绘图方法如 DrawLine 、 DrawRectangle 等结合使用。例如，可以先绘制一系列贝塞尔曲线来构建物体的轮廓，再利用其他绘图方法填充颜色和细节。

' 绘制物体轮廓的贝塞尔曲线
g.DrawBezier(pen, pt1, pt2, pt3, pt4)
 
' 使用FillEllipse方法填充物体的某些部分
Dim brush As New SolidBrush(Color.Green)
g.FillEllipse(brush, x, y, width, height)
 
' 使用DrawRectangle方法绘制物体的边缘
g.DrawRectangle(pen, x, y, width, height)

3.3 DrawBezier方法的优化技巧

3.3.1 性能优化策略

在使用 DrawBezier 方法绘制复杂图形或大量曲线时，性能可能成为关注点。优化策略包括减少不必要的绘图调用、缓存复杂图形的位图以及使用双缓冲技术。

例如，可以使用 Graphics 对象的 DrawCachedBitmap 方法来绘制预先缓存的位图，而不是每次都重新绘制整个图形。

3.3.2 错误处理和调试技巧

在复杂的绘图应用中，正确处理异常和进行调试是非常关键的。在使用 DrawBezier 方法时，必须确保所有使用的参数都是有效的，否则可能会抛出异常。

例如：

Try
    g.DrawBezier(pen, pt1, pt2, pt3, pt4)
Catch ex As Exception
    MessageBox.Show("绘制失败: " & ex.Message)
End Try

这样可以捕获并处理绘图过程中可能出现的任何异常，并向用户显示错误消息。

通过上述章节内容的详细介绍，我们了解了 DrawBezier 方法在Visual Basic中的应用，以及如何结合GUI进行高级应用，以及一些常用的优化策略。下一章节将会详细探讨贝塞尔曲线控制点的调整与平滑技术，进一步深入理解贝塞尔曲线的高级操作。

4. Bezier曲线控制点的调整与平滑技术

4.1 控制点的作用和影响

4.1.1 控制点的直观理解

Bezier曲线通过控制点来定义曲线的形状和路径。这些控制点是构成Bezier曲线的几何基础，决定了曲线的整体形态和流线。直观上，我们可以将控制点看作是"拉力点"，它们通过"拉扯"曲线来影响其弯曲程度和方向。当移动一个控制点时，与之相关的曲线部分就会相应地弯曲或者拉直，从而产生新的形状。

4.1.2 如何影响曲线的形状

控制点影响曲线的形状遵循一定的数学规则。在二次和三次Bezier曲线中，曲线的起点和终点由首尾两个控制点确定。中间的控制点则决定了曲线的弯曲程度和曲线的"方向"。对于二次Bezier曲线，仅有一个中间控制点；而对于三次Bezier曲线，有两个中间控制点。

曲线平滑的关键在于控制点的合理布局。一个曲率变化平缓的曲线，需要控制点位置适当并且均匀分布。相反，如果需要曲线出现锐利的转折，则需要将控制点紧密地放置在一起，或者把它们移动到离曲线较远的位置。通过适当的控制点调整，可以实现从简单直线到复杂曲线的各种形状。

4.2 曲线平滑技术

4.2.1 平滑算法的原理

曲线平滑技术的核心在于调整控制点的位置，使得曲线上没有尖锐的转折点，整体看起来流畅自然。通常，算法会考虑以下几个方面：

• 控制点间距离：减少控制点之间的距离能够帮助平滑曲线。
• 控制点位置：改变控制点的位置来调整曲线弯曲的程度。
• 曲率连续性：确保曲线在各个控制点处曲率变化连续，无突变。

4.2.2 实现曲线平滑的具体方法

一个常用的平滑技术是使用迭代方法来微调控制点的位置。这种方法通常包括以下步骤：

1. 对曲线上的点进行采样，确定需要平滑的区域。
2. 分析采样点的曲率，识别曲率突变的点。
3. 对于曲率突变的点，计算新的控制点位置，使得曲率变化更加平缓。
4. 使用新的控制点重新绘制曲线，再次进行采样与分析，重复步骤2和3，直到曲线达到预定的平滑度。

4.3 动态调整控制点实现交互效果

4.3.1 用户输入和控制点的关联

在许多应用中，用户希望实时看到控制点调整对曲线形状的影响，这要求程序能够动态地响应用户的输入，并实时更新控制点的位置。例如，用户通过鼠标拖动控制点来调整曲线，程序需要捕捉鼠标的移动事件，并实时计算并更新控制点的新位置。这样可以给用户一种"所见即所得"的直观体验。

4.3.2 实时更新曲线的技术实现

实现曲线的实时更新，需要高效地执行以下步骤：

1. 监听和捕捉用户的输入事件（如鼠标或触摸事件）。
2. 根据用户操作计算控制点的新位置。
3. 使用新的控制点位置重新绘制Bezier曲线。
4. 更新绘图界面，显示新的曲线形状。
5. 确保整个过程的响应速度足够快，以实现流畅的用户体验。

为了实现高效更新，可以采用以下策略：

• 预计算和缓存：预先计算可能会用到的值，并将它们存储在缓存中，从而减少实时计算负担。
• 分层渲染：将曲线的绘制分解为多个层次，先绘制底层，再绘制上层，可以优化渲染效率。
• 双缓冲技术：使用两个缓冲区，一个用于绘制，一个用于显示，可以避免在绘制过程中产生闪烁。

下面是使用HTML5 Canvas和JavaScript来动态调整Bezier曲线控制点并实时更新的简单示例代码：

// HTML部分
<canvas id="myCanvas" width="400" height="400"></canvas>
 
// JavaScript部分
const canvas = document.getElementById('myCanvas');
const ctx = canvas.getContext('2d');
 
// 初始化控制点
let controlPoints = [{x: 50, y: 200}, {x: 150, y: 100}, {x: 250, y: 300}, {x: 350, y: 200}];
 
// 绘制Bezier曲线的函数
function drawBezier() {
    ctx.beginPath();
    ctx.moveTo(controlPoints[0].x, controlPoints[0].y);
    for (let i = 1; i < controlPoints.length; i++) {
        ctx.bezierCurveTo(
            controlPoints[i].x, controlPoints[i].y,
            controlPoints[i].x, controlPoints[i].y,
            controlPoints[i].x, controlPoints[i].y
        );
    }
    ctx.stroke();
}
 
// 更新控制点位置的函数
function updateControlPoints(x, y, index) {
    controlPoints[index] = {x: x, y: y};
    drawBezier();
}
 
// 为每个控制点添加事件监听器
for (let i = 0; i < controlPoints.length; i++) {
    let cp = controlPoints[i];
    canvas.addEventListener('mousemove', (event) => {
        let rect = canvas.getBoundingClientRect();
        let mouseX = event.clientX - rect.left;
        let mouseY = event.clientY - rect.top;
        updateControlPoints(mouseX, mouseY, i);
    });
}
 
// 首次绘制曲线
drawBezier();

这段代码首先初始化了一个Canvas，并在其中绘制了初始的Bezier曲线。每个控制点在页面上用一个可拖动的点表示。当用户拖动这些点时，会触发事件监听器，进而调用 updateControlPoints 函数更新控制点位置并重新绘制曲线。这是一个简单的交互示例，展示了如何将用户输入与Bezier曲线的动态调整结合起来。

5. Bezier曲线在图形设计、游戏开发、CAD系统等领域的应用案例

5.1 Bezier曲线在图形设计中的应用

5.1.1 设计软件中的曲线工具

在图形设计中，Bezier曲线是一个不可或缺的工具。许多流行的设计软件，如Adobe Illustrator、CorelDRAW以及Affinity Designer等，都内置了强大的Bezier曲线编辑功能。设计师通过调整控制点来精确地创建平滑的曲线和复杂图形，Beizer曲线的应用使得图形设计更加灵活和高效。

5.1.2 艺术作品中的Bezier曲线实例分析

让我们通过一个艺术作品来深入了解Bezier曲线在图形设计中的应用。考虑一个现代艺术作品，例如一个由多个曲线段组成的图案，设计师在创作过程中会使用到如下步骤：

1. 利用软件中的贝塞尔曲线工具绘制基础图形。
2. 调整控制点以达到所需的曲线平滑度和形状。
3. 运用曲线工具进行变形和组合，创造出独一无二的图案。
4. 对特定曲线段进行调整，以增加视觉冲击力。

这种创作过程不仅依赖于设计师的美学直觉，更依赖于对Bezier曲线特性的深刻理解。使用Bezier曲线可以轻松创建复杂和有机的图形，这在传统的绘图方法中很难实现。

5.2 Bezier曲线在游戏开发中的应用

5.2.1 游戏中的角色动画和路径规划

Bezier曲线在游戏开发中的应用同样广泛。特别是在角色动画和路径规划中，Bezier曲线可以用来平滑地控制对象的移动轨迹。这不仅可以提高视觉效果，也可以增强玩家的游戏体验。

5.2.2 Bezier曲线优化游戏视觉效果的方法

在游戏开发中，Bezier曲线的使用包括：

1. 插值和动画：使用Bezier曲线作为关键帧之间的插值方法，以实现角色和对象的平滑动画。
2. 路径创建：通过Bezier曲线定义车辆、飞行物体或其他移动对象的路径。
3. 粒子系统：在粒子系统中控制元素的发射或爆炸轨迹。

对于如何优化游戏中的Bezier曲线应用，开发者通常会进行以下优化：

• 对曲线进行细分，以便更精确地控制动画。
• 利用缓存机制，减少重复计算，提高效率。
• 预计算关键帧之间的路径，以实现更快的动态响应。

5.3 Bezier曲线在CAD系统中的应用

5.3.1 CAD中的曲线绘制和编辑功能

CAD（计算机辅助设计）系统是工程师、建筑师和产品设计师的工具，Bezier曲线在CAD系统中提供了精确和灵活的设计能力。在这些系统中，Bezier曲线可以用于：

1. 创建和编辑精确的工程图纸。
2. 设计复杂的三维表面。
3. 优化零件和组件的轮廓形状。

CAD系统中的Bezier工具通常允许用户：

• 直观地调整控制点，实时查看曲线的变化。
• 将Bezier曲线与其他形状工具结合，创建复杂模型。
• 采用参数化设计方法，便于修改和重用设计元素。

5.3.2 提高设计效率的Beizer曲线技巧

在CAD设计中，应用Bezier曲线的一些技巧可以显著提高设计效率：

• 学习使用快捷键和命令，减少鼠标操作，提高设计速度。
• 利用CAD软件提供的预览功能，快速调整曲线形状，确保设计意图得以实现。
• 组合使用多种曲线工具，比如样条曲线、圆弧和直线，来创建更加复杂的几何形状。

以上章节展示了Bezier曲线在不同领域的应用案例，通过具体分析，我们可以发现Bezier曲线强大的实用性和灵活性，以及在设计、动画和工程中的重要性。