前言:Prim算法是图论中的算法,用来生成图的最小生成树。本篇文章介绍算法的流程,实现思想,和具体代码实现,使用c语言。学习需要输出才能理解的更透彻,所以说坚持写文章,希望可以用自己的方式把一些知识的原理描述出来。我会结合示意图清晰地展现出所有的流程,用人类语言把整个过程表述清楚,在写代码的时候才能做到胸有成竹,而不是模棱两可或者说差不多就是这样。本篇文章假设你已经具有了基本的数据结构和c语言的基础。
分享一个学习算法的神奇网站,可以可视化算法的执行过程。
Prim算法
一、Prim算法实现思路
Prim算法的作用是实现图的最小生成树。
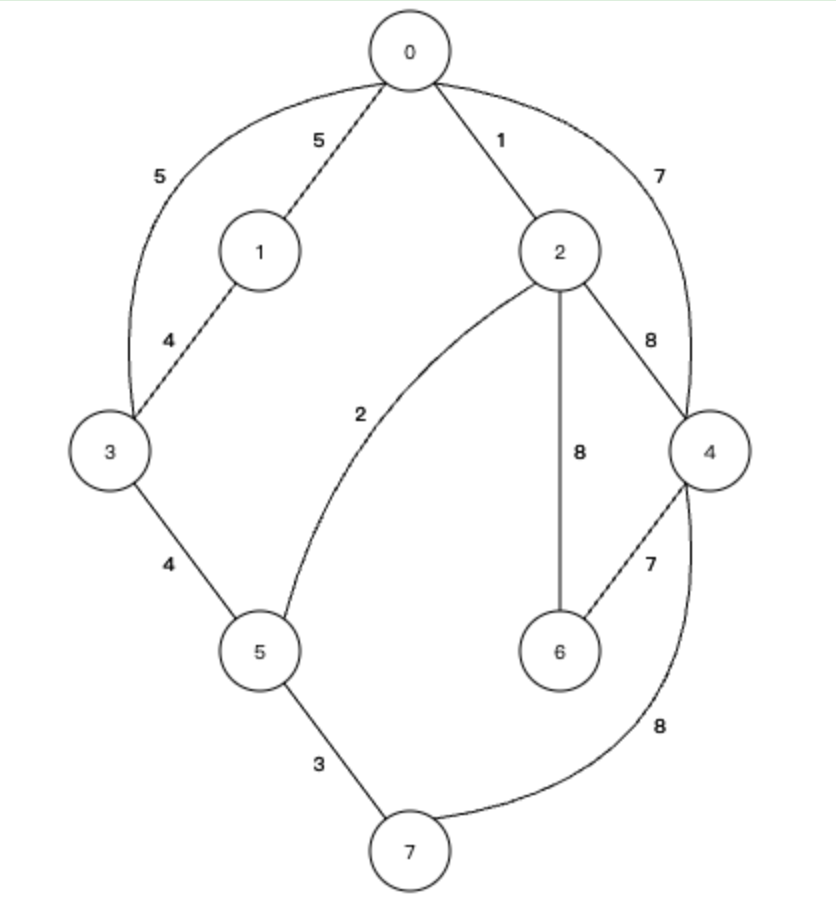
Prim算法使用的是贪心算法的策略,每次都会找和当前的节点相连的边中,权值最小的节点。以上面这个图为例,首先我们要确定最小生成树的根节点,我们就设定为0节点。下面我们分步骤进行
① 根据贪心算法的原则,与0相连的下一个节点,我们要找0节点的边中,权值最小的边,0节点相连的一共有4条边,分别是
| 起点 | 终点 | 权值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 2 | 1 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
找到权值最小的,就是连接2号节点的边,权值为1,所以会将2号节点加入到最小生成树中。
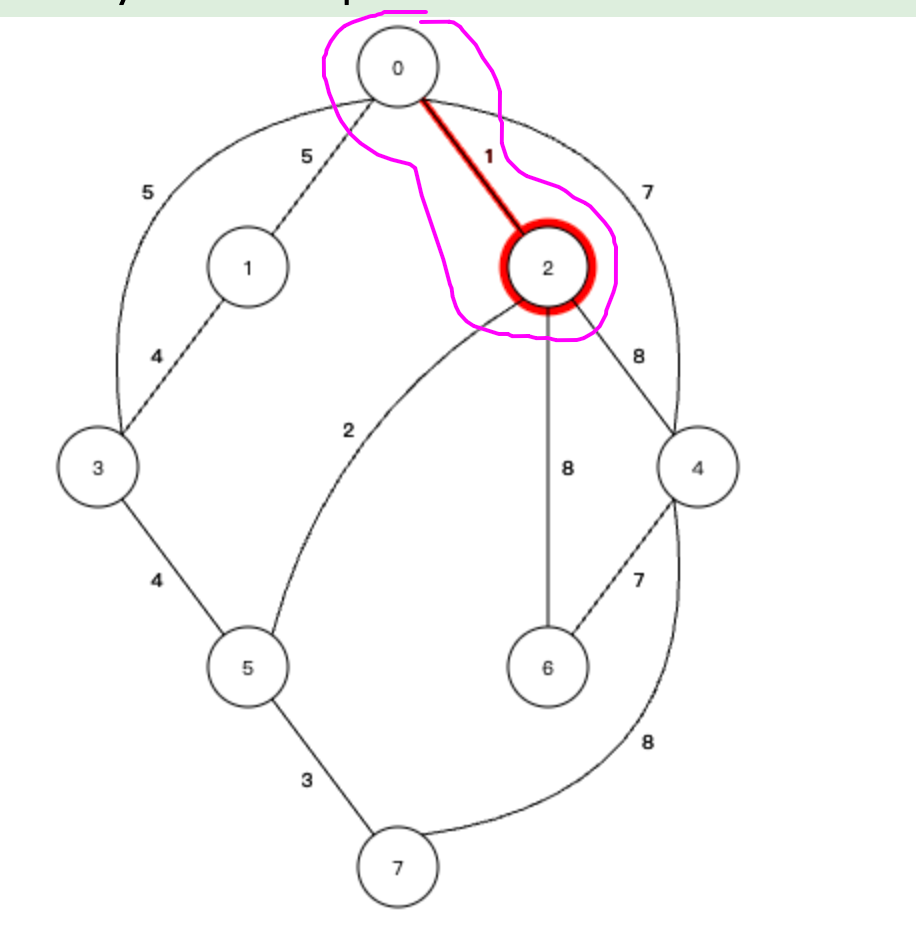
② 现在构成了图中所画的一棵生成树,需要将这两个节点看成一个整体,找和这棵生成树相连的边中,权值最小的边,所有的边:
| 起点 | 终点 | 权值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 5 | 2 |
| 2 | 6 | 8 |
最小的边就是连接2号节点和五号节点的边,权值为2,然后就将5号节点加入到生成树中,并且5号节点连的是2号节点,就会生成下面这棵生成树
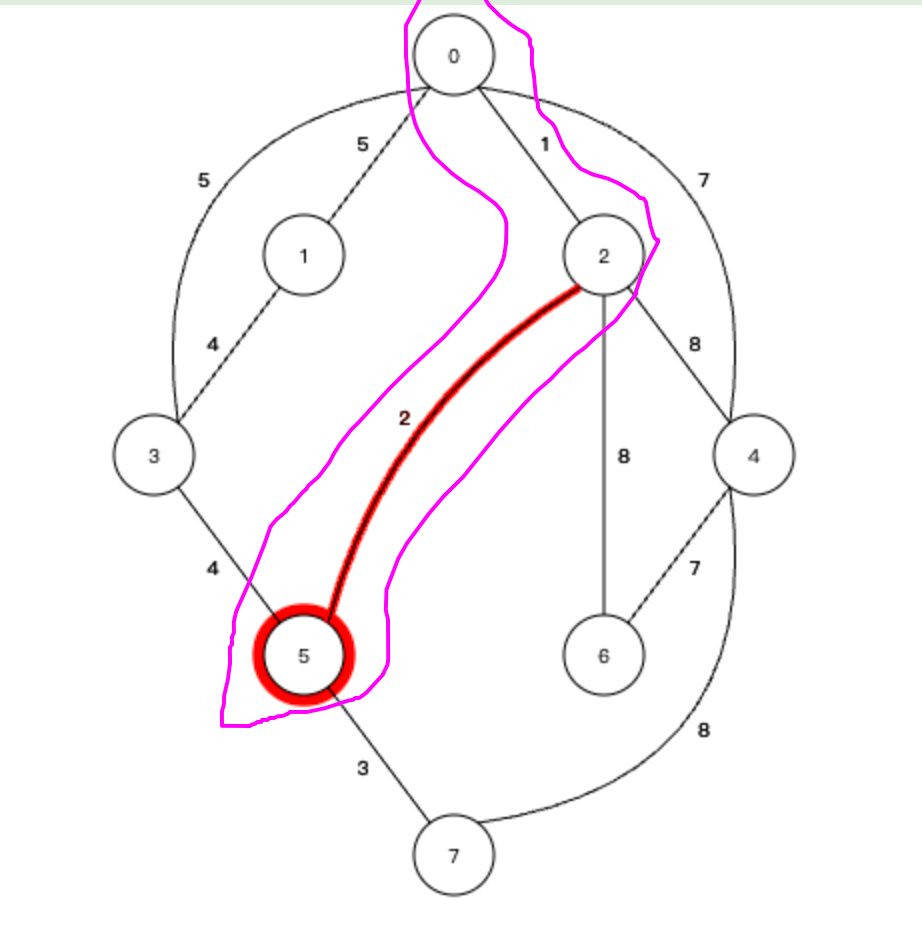
③接下来看和 1-2-5 生成树相连的节点的权值,所有的边:
| 起点 | 终点 | 权值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 5 | 7 | 3 |
| 5 | 3 | 4 |
权值最小的边就是连接5号节点和3号节点的边,权值为3,那么就将3号节点加入到生成树中,生成树如下:
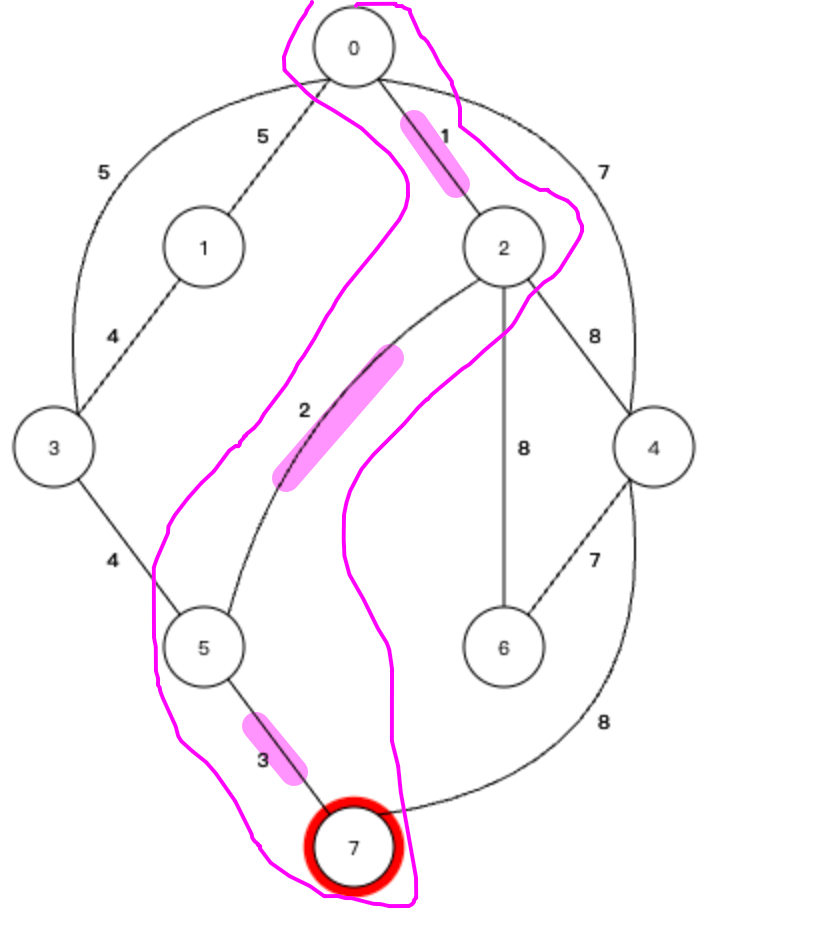
④ 再看和当前的生成树相连的所有边:
| 起点 | 终点 | 权值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 3 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 5 | 3 | 4 |
| 7 | 4 | 8 |
权值最小的边是连接5号节点和3号节点的边,权值为4,构成的生成树如下:
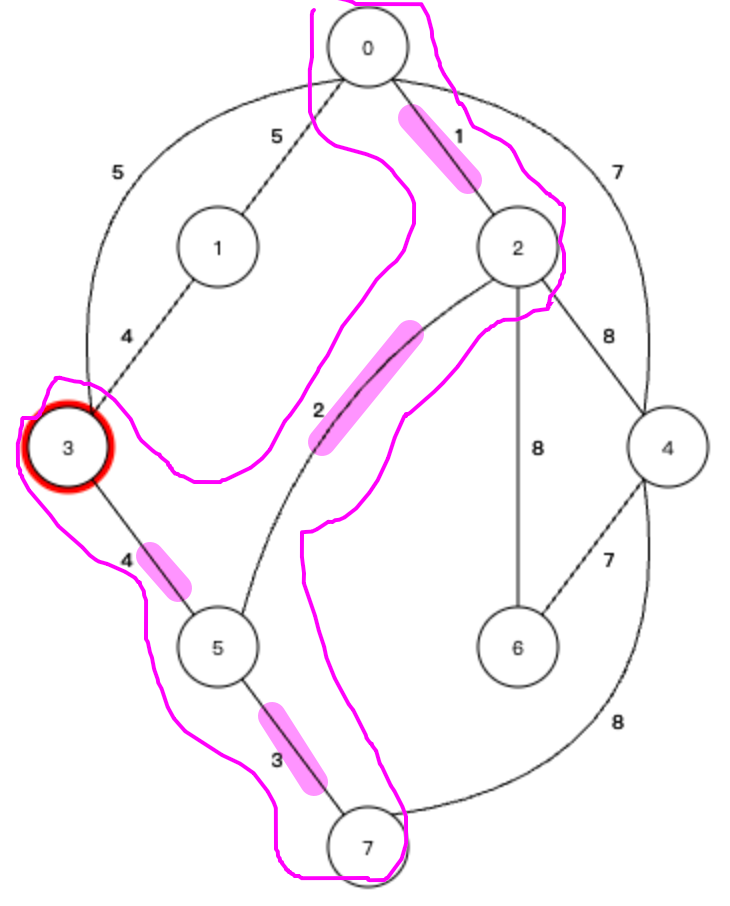
⑤ 这里有一个需要注意的地方,就是最小生成树一定是不能有环,所以从3到0的边就不能再考虑了,和当前生成树相连的边:
| 起点 | 终点 | 权值 |
|---|---|---|
| 0 | 1 | 5 |
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 7 | 4 | 8 |
| 3 | 1 | 4 |
权值最小的边是连接3号节点和1号节点的边,权值为4,那么就将1号节点加入到生成树:

⑥ 去除会形成回路的边 0 -> 5, 和当前的生成树相连的所有的边:
| 起点 | 终点 | 权值 |
|---|---|---|
| 0 | 4 | 7 |
| 2 | 4 | 8 |
| 2 | 6 | 8 |
| 7 | 4 | 8 |
| 其中权值最小的边是 连接0号节点和4号节点的边,权值为7,将4号节点加入生成树,形成下面一个生成树: |
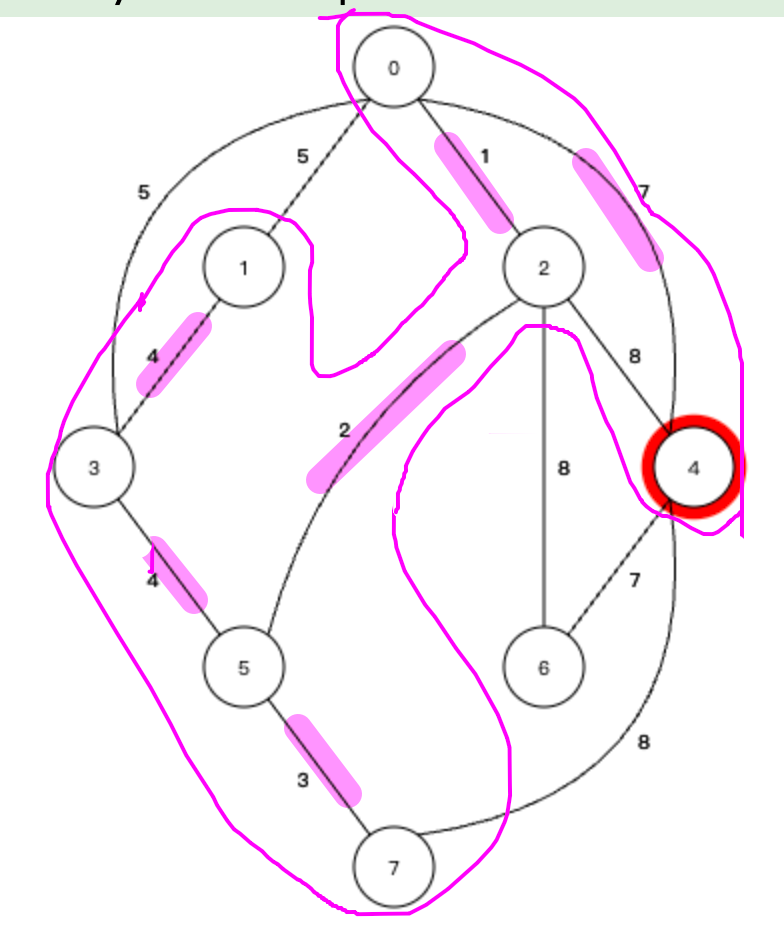
⑦ 此时的边只有两条了,因为形成回路的边要去掉
| 起点 | 终点 | 权值 |
|---|---|---|
| 2 | 6 | 8 |
| 4 | 6 | 7 |
| 选择连接4号节点和6号节点的边,权值为7,至此所有的节点添加完毕 |
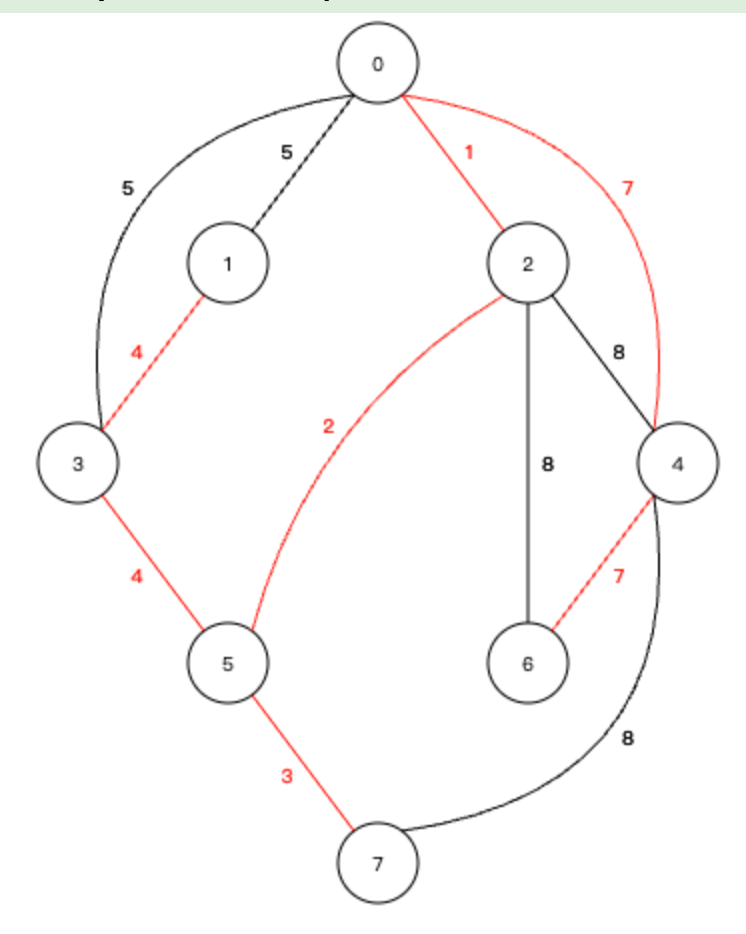
二、代码实现
通过上面的文字描述和图像展示,我们已经了解到了普利姆算法的执行的流程,接下来我们看一下代码层面的实现。分析一个问题,首先是站在人类思维像上面一样,写出步骤,然后就是需要转化成代码。这个过程还是挺复杂的,比较抽象。
一个功能的代码实现大概可以分为下面:
1、数据的类型、常量,需要定义结构体和常量,常量如最大值的限定等
2、入参
3、主函数
4、初始化辅助变量,需要分析都需要什么辅助的变量
5、流程执行
7、输出结果,printf或者return
当然关键就是第五步,其实前置的步骤都是为第五步服务的。我们先分析一下主流程需要做什么:
1、找和当前生成树相连的边中权值最小的边
2、将边加入当前生成树
3、需要记录当前的节点相连的在生成树中的节点,才能正确绘制树
那么我们就需要一个数组,来存储和当前生成树直接相连的所有的边的权值,其实就是节点到生成树的距离,如果节点在生成树内部,那么距离就是0,如果没有直接相连,那么距离就是正无穷,这个数组的名字取做 lowcost,意为最低成本的构成树,这个数组的初始化需要通过遍历邻接数组获取,我们都假设树的根节点为0号节点,那么lowcost 初始时就是0号节点到所有其他节点的距离,就是邻接数组的第一行。
需要一个数组来记录当前的节点相连的在生成树中的节点,记为 adjvex 数组,意为临近节点,初始化都为 0,
这两个数组通过下标来和节点一一对应。
然后我们需要比较生成树的边中,权值最小的边,也就是需要一个min变量,遍历所有的边,不断更新min,让它变成最小的权值,并且如果一个节点离生成树的距离最小,我们还要记录这个节点,记为 k。
k 节点需要加入到生成树中,也就是将 k 节点放在生成树中,也就是 k 节点对应的 lowcost[k] 要置为0,表示k节点到生成树的距离为0,权值和距离其实是一个意思。
将 k 节点加入到生成树中之后,还需要更新 adjvex 数组,想象一下,如果之前 0 -> 3 节点 没有路径,初始时 lowcost[3] = 正无穷,但是 0 -> 2 有路径,并且 2 -> 3 有路径,此时就需要更新 3 节点相连的节点,也就是 adjvex[3] 修改成 2,lowcost[3] = 2到3的距离,但是如果后面4号节点加入树,并且 4-> 3 的路径更短了,那就需要修改 adjvex[3] = 4,lowcost[3] = 4到3的距离。所以说需要对比从 k 到 j 的距离和当前的 lowcost[j],如果k 到 j 的距离更小,需要更新lowcost[j] = k到j的距离和adjvex[j] = k 。
上面流程走完之后,是实现了第一个权值最小的边的节点加入到生成树,所以整体需要循环n次,n为树的节点数
接下来根据主流程分析一下需要初始化的数据:
1、需要两层循环,i、j 作为循环变量
2、需要一个 min 值,初始化为一个c语言中的最大值
3、k 记录权值最小的边对应的节点
4、lowcost 数组,记录权值
5、adjvex 数组,记录邻近节点
需要定义的数据结构和常量:
1、图的结构体
2、MAXVEX 表示最大节点数
入参就是 图
接下来看实际的代码吧,相信通过上面的分析你已经非常清楚每句代码的作用
c
// 普利姆算法
#include <stdio.h>
#include <limits.h>
#define MAXVEX 100 // 最大顶点数
// 图的邻接矩阵表示
typedef struct {
int vexnum; // 顶点数
int arcnum; // 边数
int arcs[MAXVEX][MAXVEX]; // 邻接矩阵
} MGraph;
void MiniSpanTree_Prim(MGraph G){
int min,i,j,k;
int adjvex[MAXVEX]; // 保存邻接顶点下标的数组
int lowcost[MAXVEX]; // 记录当前生成树到剩余顶点的最小权值
lowcost[0] = 0; // 初始化第一个权值为0,即v0加入生成树
adjvex[0] = 0; // 将0号顶点作为第一个顶点加入到树中
for(i=1;i<G.vexnum;i++){ // 除了下标为0以外的所有顶点
lowcost[i] = G.arcs[0][i]; // 将与下标为0的顶点有边的权值存入lowcost数组
adjvex[i] = 0; // 这些顶点的adjvex数组元素都为0
}
// 算法核心
for(i=1;i<G.vexnum;i++){ // 只需要循环vexnum-1次
min = INT_MAX; // 使用更合适的最大值
j=0;k=0;
// 找出lowcost中最小值,最小权值给min,最小值的下标给k
for(j=1;j<G.vexnum;j++){ // 从1号顶点开始找
if(lowcost[j]!=0 && lowcost[j]<min){ // 不在生成树中的顶点而且权值更小的
min = lowcost[j]; // 更新更小的值
k = j; // 找q到了新的点下标给k
}
}
printf("边(%d,%d) 权值:%d\n",adjvex[k],k,min); // 打印权值最小的边
lowcost[k] = 0; // 将这个顶点加入生成树
for(j=1;j<G.vexnum;j++){
if(lowcost[j]!=0 && G.arcs[k][j]<lowcost[j]){ // 如果新加入的顶点k使权值更小
lowcost[j] = G.arcs[k][j]; // 更新更小的权值
adjvex[j] = k; //修改这条边邻接的顶点
}
}
}
}
// 初始化测试图
void initTestGraph(MGraph *G) {
int i, j;
// 初始化邻接矩阵为无穷大(用大数值表示)
for(i = 0; i < MAXVEX; i++) {
for(j = 0; j < MAXVEX; j++) {
if(i == j) {
G->arcs[i][j] = 0; // 自己到自己距离为0
} else {
G->arcs[i][j] = INT_MAX; // 无边用最大值表示
}
}
}
// 设置顶点数
G->vexnum = 6; // 0-5共6个顶点
// 添加边(无向图,需要设置两个方向)
// 边 0-1,权值4
G->arcs[0][1] = G->arcs[1][0] = 4;
// 边 0-2,权值6
G->arcs[0][2] = G->arcs[2][0] = 6;
// 边 0-3,权值16
G->arcs[0][3] = G->arcs[3][0] = 16;
// 边 1-2,权值10
G->arcs[1][2] = G->arcs[2][1] = 10;
// 边 1-4,权值7
G->arcs[1][4] = G->arcs[4][1] = 7;
// 边 2-3,权值14
G->arcs[2][3] = G->arcs[3][2] = 14;
// 边 2-4,权值3
G->arcs[2][4] = G->arcs[4][2] = 3;
// 边 2-5,权值8
G->arcs[2][5] = G->arcs[5][2] = 8;
// 边 4-5,权值9
G->arcs[4][5] = G->arcs[5][4] = 9;
}
int main() {
MGraph G;
printf("=== 普里姆最小生成树算法演示 ===\n\n");
// 初始化测试图
initTestGraph(&G);
printf("图的顶点数:%d\n", G.vexnum);
printf("图的边信息:\n");
printf("0-1: 4, 0-2: 6, 0-3: 16\n");
printf("1-2: 10, 1-4: 7\n");
printf("2-3: 14, 2-4: 3, 2-5: 8\n");
printf("4-5: 9\n\n");
printf("开始执行普里姆算法:\n");
printf("最小生成树的边:\n");
// 执行普里姆算法
MiniSpanTree_Prim(G);
printf("\n================================\n");
printf("算法执行完成!\n");
printf("实际结果:总权值 = 4+6+3+8+14 = 35\n");
return 0;
}