分治算法---归并

cpp 复制代码

class Solution 
{
    vector<int> tmp;
public:
    vector<int> sortArray(vector<int>& nums) 
    {
        tmp.resize(nums.size());
        mergeSort(nums,0,nums.size() - 1);
        return nums;
    }
    void mergeSort(vector<int>& nums, int left , int right)
    {
        if(left >= right) return;
        int mid = (left + right) >> 1;
        mergeSort(nums,left, mid);
        mergeSort(nums,mid + 1, right);
        int cur1 = left;
        int cur2 = mid+1;
        int i = 0;
        while((cur1 <= mid)&&(cur2 <= right))
        {
            if(nums[cur1]>nums[cur2])
            {
                tmp[i++] =  nums[cur2++];
            }
            else
            {
                tmp[i++] = nums[cur1++];
            }
        }
        while(cur1 <= mid)
        {
            tmp[i++] = nums[cur1++];
        }
          while(cur2 <= right)
        {
            tmp[i++] = nums[cur2++];
        }
        for(int i = left; i <= right;i++)
        {
            nums[i] = tmp[i - left];
        }
    }
};

2、数组中的逆序对

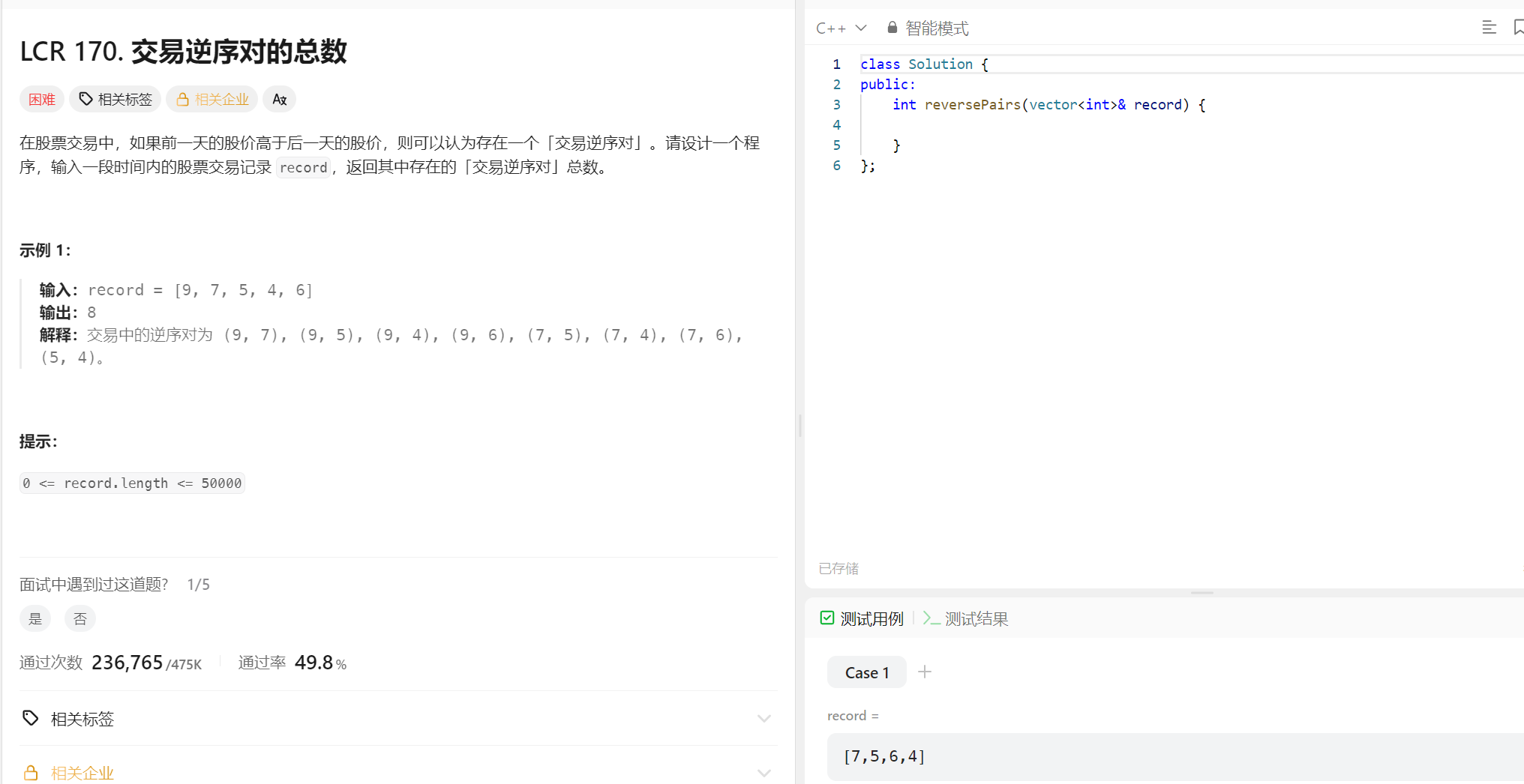
（2）解题思路

方法一：暴力解法，一个一个的寻找，虽然可以找到，但是会超时

方法二：归并

我们可以先找左边部分的逆序对，再找右半部分逆序对，最后再找一左一右的，如果我们可以找的途中还能排序，会使最后一步非常的简单变成了左半部分 -》左排序 -》右半部分 -》右排序 -》一左一右，这和归并算法的思想差不多

cpp 复制代码

class Solution 
{
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) 
    {
        return mergeSort(nums,0,nums.size() - 1);
    }
    int mergeSort(vector<int>& nums, int left, int right)
    {
        if(left>=right) return 0;
        int ret = 0;
        int mid = (left + right) >> 1;
        ret += mergeSort(nums,left,mid);
        ret += mergeSort(nums,mid+1,right);
        int i = 0;
        int cur1 = left;
        int cur2 = mid + 1;
        while(cur1 <=  mid && cur2 <= right)
        {
            if(nums[cur1] <= nums[cur2])
            {
                tmp[i++] = nums[cur1++];
            }
            else
            {
                ret +=  mid - cur1 + 1;
                tmp[i++] = nums[cur2++];
            }
        }
        while(cur1<=mid)
        {
            tmp[i++] = nums[cur1++];
        }
        while(cur2<=right)
        {
            tmp[i++] = nums[cur2++];
        }
        for(int j = left; j<=right; j++)
        {
            nums[j] = tmp[j -left];
        }
        return ret;
    }
};

3、计算右侧小于当前元素的个数

方法一：暴力解法

方法二：和上述的算法差不多,先算左边的数,在算右边的数,再算左右两边,右侧小于当前元素的个数

cpp 复制代码

class Solution 
{
    vector<int> tmp;
    vector<int> init;
    vector<int> ret;
    vector<int> tmpinit;
public:
    vector<int> countSmaller(vector<int>& nums) 
    {
        tmp.resize(size(nums));
        init.resize(size(nums));
        ret.resize(size(nums));
        tmpinit.resize(size(nums));
        for(int i = 0; i<nums.size();i++)
        {
            init[i] = i;
        }
         mergeSort(nums,0,nums.size() - 1);
         return ret;
    }
    void mergeSort(vector<int>& nums, int left , int right)
    {
        if(left>=right)
        {
            return ;
        }
        int mid = (left + right)>>1;
        mergeSort(nums,left,mid);
        mergeSort(nums, mid+1,right);
        int cur1 = left;
        int cur2 = mid+1;
        int i =0;
        while(cur1<=mid && cur2<=right)
        {
            if(nums[cur1]>nums[cur2])
            {
                ret[init[cur1]]+= right - cur2 +1;
                    tmp[i] = nums[cur1];
                tmpinit[i++] = init[cur1++];  
            }
            else
            {
                tmp[i] = nums[cur2];
                tmpinit[i++] = init[cur2++];  
            }
            
        }
        while(cur1<=mid)
        {
            tmp[i] = nums[cur1];
            tmpinit[i++] = init[cur1++];  
        }
         while(cur2<=right)
        {
            tmp[i] = nums[cur2];
            tmpinit[i++] = init[cur2++];  
        }
        for(int i = left ; i <= right; i++)
        {
            nums[i] = tmp[i-left];
            init[i] = tmpinit[i-left];
        }
    }
};

5、翻转对

cpp 复制代码

class Solution 
{
    vector<int> tmp;
public:
    int reversePairs(vector<int>& nums) 
    {
        tmp.resize(size(nums));
        return mergeSort(nums,0,nums.size()-1);
    }
    int mergeSort(vector<int>& nums, int left, int right)
    {
        int ret = 0;
        if(left>=right) return 0;
        int mid = (left + right) >> 1;
        ret += mergeSort(nums,left,mid);
        ret += mergeSort(nums,mid+1,right);
        int cur1 = left; 
        int cur2 = mid+1;
        int i = 0;
        while(cur1<=mid)
        {
            while(cur2<=right&&nums[cur2]>=nums[cur1]/2.0)
                  cur2++;
            if(cur2 > right)
                 break;
            ret += right - cur2 +1;
            cur1++;
        } 
        cur1 = left;
        cur2 = mid + 1;
        while(cur1 <=  mid && cur2 <= right)
        {
            if(nums[cur1] <= nums[cur2])
            {
                tmp[i++] = nums[cur2++];
            }
            else
            {

                tmp[i++] = nums[cur1++];
            }
        }
        while(cur1<=mid)
        {
            tmp[i++] = nums[cur1++];
        }
        while(cur2<=right)
        {
            tmp[i++] = nums[cur2++];
        }
        for(int j = left; j<=right; j++)
        {
            nums[j] = tmp[j -left];
        }
        return ret;
    }
};