往篇内容:
一、C++编译阶段※
二、入门案例解析
三、命名空间详解
四、C++程序结构
五、函数基础
六、标识符
七、数据类型
补充:二进制相关的概念
sizeof 运算符简介
补充:原码、反码和补码
补充:ASCII码表
八、内存构成
补充:变量
九、指针基础
十、const关键字
十一、枚举类型
十二、 类型转换
十三、define指令
十四、typedef关键字
十五、运算符
十六、 流程控制
目录
十七、数组
1、数组的概述
表示一块连续的内存空间,可以用来从存储多个数据元素,要求类型一致。
定义:数据类型 数据名[常量表达式]
数组下标区间: [0,数组长度-1]
数组越界:
在 C++ 中, 数组越界 是一个常见但非常危险的错误,可能导致程序崩溃、数据损坏甚至安全漏洞。
典型场景:
cppint arr[5]; // 错误:i 最大到 5,越界访问 arr[5] for (int i = 0; i <= 5; ++i) { arr[i] = i; }数组越界的后果
- 未定义行为( Undefined Behavior )
C++ 标准不定义数组越界行为,程序可能表现异常,但不会立刻崩溃- 内存损坏
越界写入会覆盖相邻内存区域的数据,导致变量值被篡改或程序逻辑错误- 程序崩溃
如果越界访问触发操作系统的内存保护机制(如访问受保护的地址),程 序会崩溃(如 segmentation fault)。- 安全漏洞
缓冲区溢出攻击(Buffer Overflow )利用数组越界漏洞执行恶意代码。
例如:通过精心构造输入覆盖函数返回地址,劫持程序执行流程。- 难以定位的错误
越界错误可能在程序运行后期才暴露,导致调试困难。
示例:某次越界写入覆盖了关键变量,后续逻辑错误才导致崩溃。
2、数组初始化
在创建数组的同时,直接初始化数组元素的值,称为数组的初始化。
初始化格式 :
数据类型 数组名[ 常量表达式] = {元素1,元素2,...};
其中,数组长度(常量表达式)也可以省略
数据类型 数组名[] = {元素1,元素2,...};
3、数组名传参
++数组名传参本质为指针传递。++
当数组名作为函数参数传递时,实际上传递的是 数组首元素的地址 ,即一个指针
例如: void func(int arr[]) 实际上会被编译器视为 void func(int* arr)
这意味着:
- 函数内部操作的是原数组的地址,而非数组的副本;
- 数组元素的修改会直接影响原数组。
传参常见方式
- 语法: void func(int* arr, int size);
数组首元素地址,长度 - 传递的是数组首元素的地址;
- ++需要额外传递数组长度( size )以便函数内部遍历数组。++
示例:
cpp
#include<iostream>
using namespace std;
void outArray(int arr[], int len) {
for(int i=0; i<len; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
int array[8];
for(int i=0; i<8; i++)
array[i] = i;
int len = sizeof(array)/sizeof(int);
outArray(array, len);
return 0;
}4、数组使用案例
①数组反转
cpp
#include <iostream>
#include "fanzhuan.h"
using namespace std;
// 反转数组
void reverseArray(int arr[], int len) {
for (int i = 0; i < len / 2; i++) {
// 交换arr[i]和arr[len-1-i]的值
arr[i] = arr[i] ^ arr[len - i - 1];
arr[len - i - 1] = arr[i] ^ arr[len - 1 - i];
arr[i] = arr[i] ^ arr[len - 1 - i];
}
}
// 遍历数组
void outArray(int arr[], int len) {
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
// 准备数组
int arr[10];
int num = 0;
for (int i = 0; i < 10; i++) {
arr[i] = num;
num += 2;
}
int len = sizeof(arr) / sizeof(int);
outArray(arr, len);
reverseArray(arr, len);
outArray(arr, len);
return 0;
}②二分查找
二分查找的核心思想
在一个有序序列 中查找某个元素,将n个元素分成个数大致相同的两半,取a[n/2]与欲查 找的x作比较,如果x=a[n/2]则找到x,算法终止;如果x<a[n/2],则我们只要在 数组a的左半部继续搜索x;如果x>a[n/2],则我们只要在数组a的右半部继续搜索x。
分治策略
将搜索区间分为两部分,通过比较目标值与中间元素的大小关系,确定目标值可能存在的区间。每次比较后,搜索区间减半。
时间复杂度
二分查找的时间复杂度为 O(log n),远优于线性查找的 O(n)。这是因为每次迭代都将问题规模减半。
关键条件
- 数据必须有序:二分查找依赖数据的顺序性,否则无法保证正确性。
- 随机访问:需要支持通过索引直接访问元素(如数组),链表等结构不适用。
实现步骤
- 初始化左右边界(通常为
left = 0,right = n-1)。 - 计算中间索引
mid = left + (right - left) / 2(避免整数溢出)。 - 比较目标值与
arr[mid]:- 若相等,返回
mid。 - 若目标值较小,调整右边界
right = mid - 1。 - 若目标值较大,调整左边界
left = mid + 1。
- 若相等,返回
- 重复步骤 2-3 直至找到目标或区间无效(
left > right)。
cpp
#include <iostream>
using namespace std;
int binarySearch(int arr[], int len, int value)
{
int start = 0;
int end = len - 1;
int mid;
while (true)
{
mid = (start + end) / 2;
if (value == arr[mid])
{
return mid;
}
else if (value > arr[mid])
{
start = mid + 1;
}
else
{
end = mid - 1;
}
//当start > end 循环结束
if (start > end)
break;
}
return -1;
}
int main()
{
int arr[] = {1, 3, 4, 5, 7, 9, 10};
int len = sizeof(arr) / sizeof(int);
int index = binarySearch(arr, len, 1);
cout << "1: " << index << endl;
index = binarySearch(arr, len, 2);
cout << "2: " << index << endl;
index = binarySearch(arr, len, 10);
cout << "10: " << index << endl;
return 0;
}③冒泡排序
冒泡(Bubble Sort) 排序是一种简单排序算法,它通过依次比较交换两个相邻元素实现功能。每一次冒泡会让至少一个元素移动到它应该在的位置 上,这样 n 次冒泡就完成了 n 个数据的排序工作。 这个算法的名字由来是因为越小的元素会经由交换慢慢 " 浮 " 到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名" 冒泡排序 " 。
冒泡排序算法实现步骤:
- 比较相邻的元素,如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素重复上述工作,从第一对到最后一对。完成后,最大的
数会放到最后位置。 - 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要
比较。
cpp
#include <iostream>
using namespace std;
void outArray(int arr[], int len) {
for(int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
//冒泡排序
void bubbleSort(int arr[], int len) {
//每次排序,可以将 未排序序列中 最大值 放到最后位置
//len个成员,一共排序len-1次即可
for(int i = 0; i < len-1; i++) {
//每次排序,借助交换 相邻两个数,实现 最大值移动到最后位置
for(int j = 0; j < len-1-i; j++) {
if(arr[j] > arr[j+1]) {
arr[j] = arr[j] ^ arr[j+1];
arr[j+1] = arr[j] ^ arr[j+1];
arr[j] = arr[j] ^ arr[j+1];
}
}
cout << "第" << (i+1) << "次排序后: ";
outArray(arr,len);
}
}
int main() {
int array[] = {4,5,3,2,1};
int size = sizeof(array) / sizeof(int);
//排序
bubbleSort(array,size);
cout << "排序完成后: " << endl;
//遍历
outArray(array,size);
return 0;
}④插入排序
用于对少量元素的排序
算法描述:
- 将数组分成两部分,已排序、未排序区间,初始情况下,已排序区间只有一个元素,即数组第一个元素;
- 取未排序区间中第一个元素,插入到已排序区间中合适的位置,这样子就得到了一个更大的已排序区间;
- 重复这个过程,直到未排序区间中元素为空,算法结束。插入排序过程见下图:
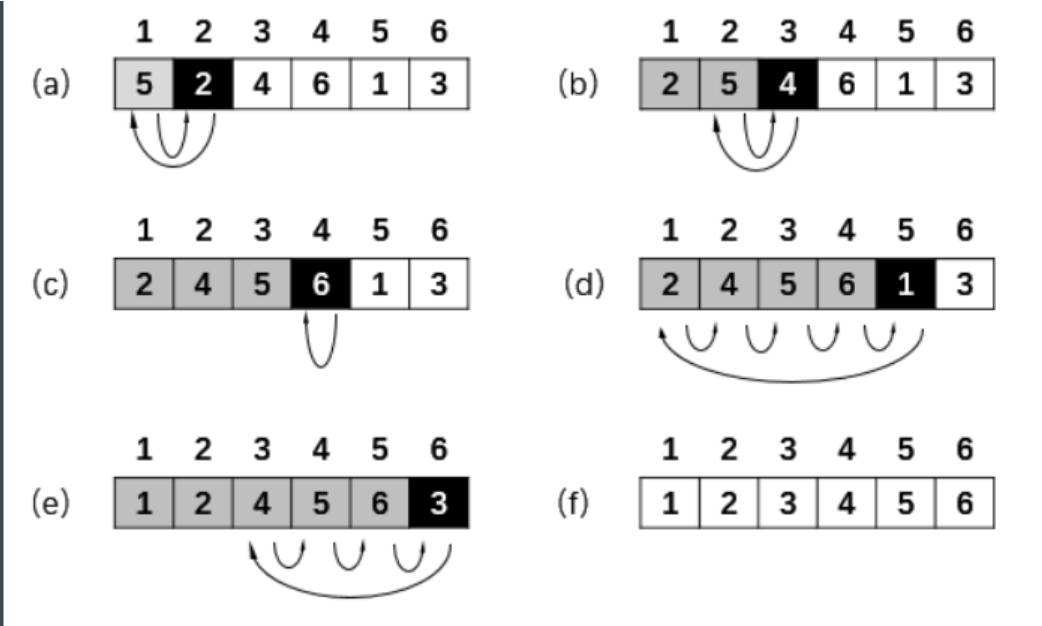
cpp
#include <iostream>
using namespace std;
// 遍历数组 函数声明
void printArray(int arr[], int len);
// 插入排序 函数声明
void insertSort(int arr[], int len);
int main() {
// 准备一个int数组
int array[] = {5, 2, 6, 9, 0, 3};
int len = sizeof(array) / sizeof(int);
cout << "排序前: ";
printArray(array, len);
// 插入排序
insertSort(array, len);
// 输出排序结果
cout << "排序后: ";
printArray(array, len);
return 0;
}
void insertSort(int arr[], int len) {
if (len <= 1) {
return;
}
// 外层循环控制 总体循环次数
for (int i = 1; i < len; i++) {
// 内层循环做的事情:将无序列表中第一个元素插入到有序列表中合适位置
int value = arr[i];
// 获取有序列表中最后一个元素下标
int j = i - 1;
for (; j >= 0; j--) {
if (value < arr[j]) {
arr[j + 1] = arr[j];
} else {
break;
}
}
// 将需要插入的元素 放置到合适位置
arr[j + 1] = value;
// 一次排序完成后,输出 方便 观察
cout << "第 " << i << "次排序: ";
printArray(arr, len);
}
}
void printArray(int arr[], int len) {
for (int i = 0; i < len; i++) {
cout << arr[i] << " ";
}
cout << endl;
}⑤选择排序
选择排序(Selection Sort) 的原理有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾,最终完成排序。
算法描述:
- 初始状态:无序区间为 Arr[0.1..n] ,有序区间为空 ;
- 第 i==1 趟排序开始,从无序区中选出最小的元素 Arr[k] ,将它与无序区的第
1 个元素交换,从而得到有序区间 Arr[0..i-1], 无序区间 Arr[i..n]; - 继续后面第 i 趟排序 (i=2,3...n-1) ,重复上面第二步过程 ;
- 第 n-1 趟排序结束,数组排序完成。
选择排序过程如下图:

cpp
#include <iostream>
using namespace std;
// 遍历数组 函数声明
void printArray(int arr[], int len);
// 选择排序 函数声明
void selectSort(int arr[], int len);
int main()
{
// 准备一个int数组
int array[] = {5, 2, 6, 9, 0, 3};
int len = sizeof(array) / sizeof(int);
cout << "排序前: ";
printArray(array, len);
// 选择排序
selectSort(array, len);
// 输出排序结果
cout << "排序后: ";
printArray(array, len);
return 0;
}
void selectSort(int arr[], int len)
{
if (len <= 1)
return;
// 外层循环控制总体排序次数
for (int i = 0; i < len - 1; i++)
{
int minIndex = i;
// 内层循环找到当前无序列表中最小下标
for (int j = i + 1; j < len; j++)
{
if (arr[minIndex] > arr[j])
{
minIndex = j;
}
}
// 将无序列表中最小值添加到有序列表最后位置
if (minIndex != i)
{
arr[minIndex] = arr[minIndex] ^ arr[i];
arr[i] = arr[minIndex] ^ arr[i];
arr[minIndex] = arr[minIndex] ^ arr[i];
}
cout << "第 " << i << " 次排序: ";
printArray(arr, len);
}
}
void printArray(int arr[], int len)
{
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}⑥希尔排序
希尔 (shell) 排序是 Donald Shell 于 1959 年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2 )的第一批算法之一。
希尔排序对直接插入排序改进的着眼点:
- 若待排序序列中 元素基本有序时,直接插入排序的效率可以大大提高
- 如果待排序序列中 元素数量较小时,直接插入排序效率很高
希尔排序算法思路:
将整个待排序序列分割成若干个子序列 ,在子序列内部分别进行 直接插入排 序 ,等到整个序列 基本有序 时,再对全体成员进行直接插入排序!
待解决问题:
- 如何分割子序列,才能保证最终能得到基本有序?
- 子序列内部如何进行直接插入排序?

分割方案
- 将有 n 个元素的数组分成 n/2 个数字序列,第 i 个元素和第 i+n/2 , i+n/2*m...
个元素为一组; - 对一组数列进行简单插入排序;
- 然后,调整增量为 n/4, 从而得到新的几组数列,再次排序;
- 不断重复上述过程,直到增量为 1 , shell 排序完全转化成简单插入排序,
完成该趟排序,则数组排序成功。
希尔排序流程:
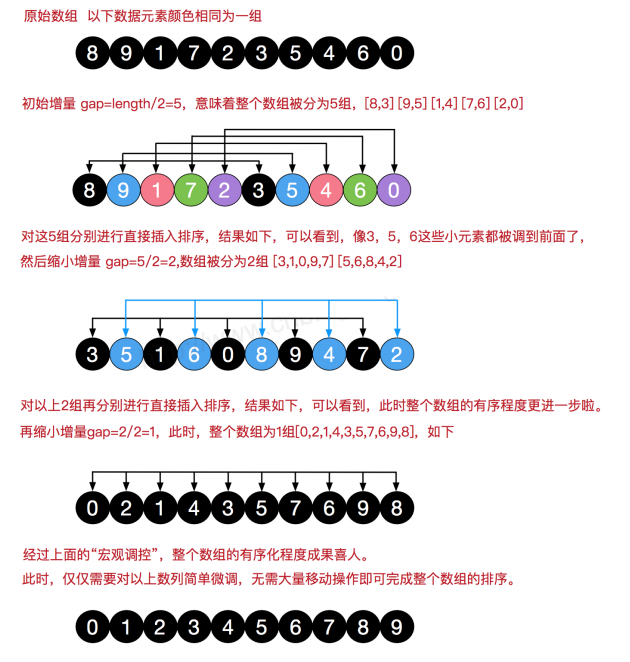
cpp
#include <iostream>
using namespace std;
// 遍历数组 函数声明
void printArray(int arr[], int len);
// 希尔排序 函数声明
void shellSort(int arr[], int len);
int main()
{
// 准备一个int数组
int array[] = {5, 2, 6, 9, 0, 3};
int len = sizeof(array) / sizeof(int);
cout << "排序前: ";
printArray(array, len);
// shell排序
shellSort(array, len);
// 输出排序结果
cout << "排序后: ";
printArray(array, len);
return 0;
}
void shellSort(int arr[], int len)
{
if (len <= 1)
return;
// 设置初始增量
int gap = len / 2;
// 定义排序次数
int count = 0;
// 由增量控制整体排序次数
while (gap > 0)
{
// 插入排序改造
for (int i = gap; i < len; i++)
{
// 记录要插入的值
int value = arr[i];
// 有序序列的最后一个元素下标
int j = i - gap;
for (; j >= 0; j -= gap)
{
if (value < arr[j]) {
arr[j + gap] = arr[j];
} else {
break;
}
}
arr[j + gap] = value;
}
count++;
cout << "第 " << count << " 次排序: ";
printArray(arr, len);
gap = gap / 2;
}
}
void printArray(int arr[], int len)
{
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}5、二维数组
二维数组可以看成是由一维数组作为数组元素 的一维数组。 如果把普通的数组(一维数组),看作一个小盒子的话,盒子里面可以存放很多数据,那么二维数组就是像一个大点的盒子,里面可以存放很多小盒子(一维数组)。
①定义格式
1)数据类型 数组名[一维长度m][二维长度n];
m :表示二维数组的元素数量,即可以存放多少个一维数组;
n :表示每一个一维数组,可以存放多少个元素;
m 、 n 均为常量表达式
2)数据类型 数组名 [] [二维长度n];
可以省略一维长度
②元素访问
书写格式:
二维数组名 [ 一维下标 m][ 二维下标 n];
③内存结构
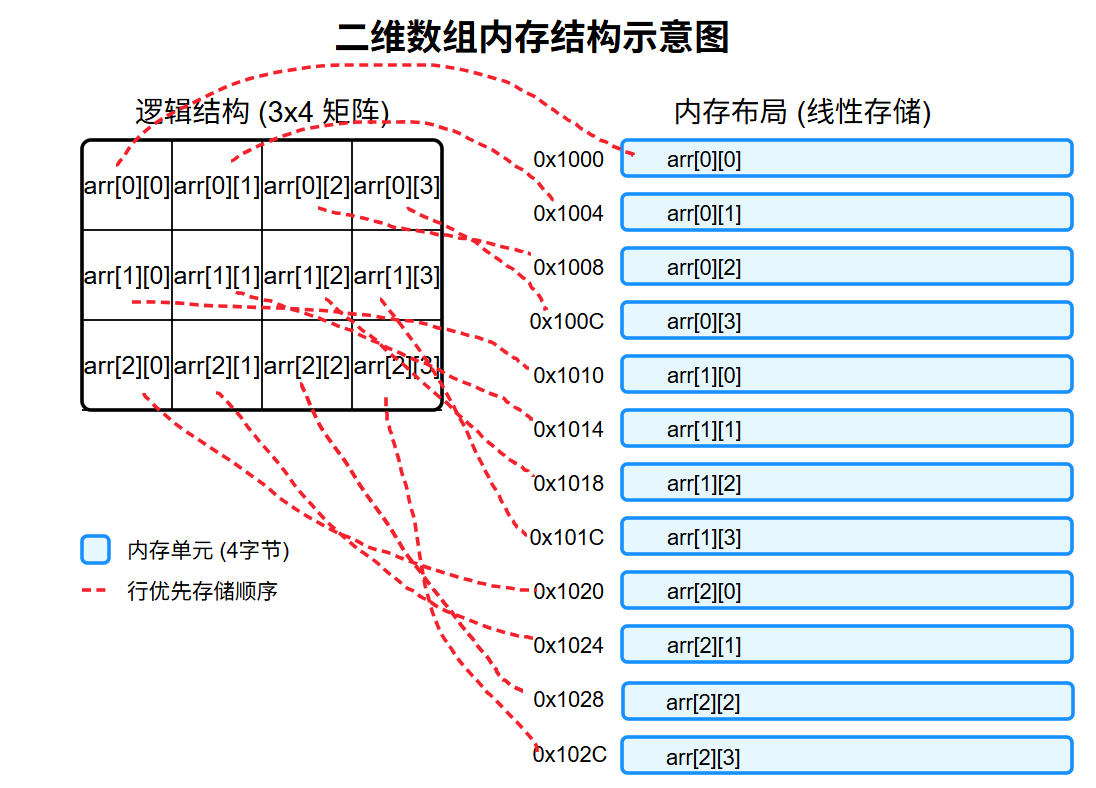
这个 SVG 图像展示了二维数组在内存中的存储方式:
- 左侧为逻辑上的 3 行 4 列矩阵结构
- 右侧为实际在内存中的线性存储方式(行优先存储)
- 每个内存单元标注了对应的数组元素和假设的内存地址(假设每个元素占 4 字节)
- 红色虚线表示逻辑结构到内存布局的映射关系
二维数组在内存中是连续存储的,通过行优先的方式将多维结构映射到一维内存空间。
④二位数组的初始化
二维数组的静态初始化,有点类似一维数组的初始化,具体格式如下:
格式 1 :分行赋值
数据类型 数组名[m][n] = { { 元素 1, 元素 2...} , { 元素 1, 元素2...}, ...};
例如:
格式 2 :部分赋值
数据类型 数组名[m][n] = { { 元素 1, 元素 2...} , { 元素 1, 元素2...} ...};
例如:
注意:未明确值的元素默认值为 0 。
格式 3 :全部元素赋值
数据类型 数组名[m][n] = { 元素 1, 元素 2,..., 元素 n};
或
数据类型 数组名[][n] = { 元素 1, 元素 2,..., 元素 n};
注意:系统会根据数据总个数分配存储空间,从而确定第一维 m的值。
例如:
int arr [ 3 ][ 4 ] = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 };
或
int arr [][ 4 ] = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 };
长度计算公式:
- 行数 = sizeof(arr) / sizeof(arr[0])
sizeof(二维数组名) 可以获取整个二维数组的长度
sizeof(二维数组名[0]) 可以获取二维数组每个元素(一维数组)的长度
- 列数 = sizeof(arr[0]) / sizeof(arr[0][0])
⑤二维数组的遍历
cpp
#include <iostream>
using namespace std;
// 函数声明
void printArray(int arr[][4], int rows);
// ok
//void printArray(int arr[3][4], int rows);
// error
//void printArray(int arr[][], int rows, int cols);
int main()
{
// 定义一个 3 行 4 列的二维数组
int matrix[3][4] = {
{1, 4},
{8},
{9, 10, 12}
};
// 调用函数打印数组
printArray(matrix, 3);
return 0;
}
// 函数定义:打印二维数组
void printArray(int arr[][4], int rows)
{
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < 4; ++j)
{
cout << arr[i][j] << " ";
}
cout << endl;
}
}注意:如果用二维数组名作为函数形参,则声明 二维数组作为参数时,必 须指定第二维的大小 ,且应与实参的第二维的大小相同。第一维的大小可以指定,也可以不指定。
⑥案例:使用二维数组创建杨辉三角并输出
cpp
#include <iostream>
using namespace std;
int main()
{
int arr[5][5] = {0};
// 根据规律,构造出二维数组并且赋值
for (int i = 0; i < 5; i++)
{
// 循环给二维数组中的每个位置赋值
for (int j = 0; j < 5; j++)
{
if (j == 0 || j == i)
{
arr[i][j] = 1;
}
else if (i > j)
{
// 除了下标中的0和最后一个,其他的元素都具备相同的规律
// 这个位置的值=上一层和它相同下标的值+前一个元素的值
arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
}
}
}
// 把赋值完成的二维数组按要求进行输出
for (int i = 0; i < 5; i++)
{
// 1.控制每行开始输出的空格
for (int j = 0; j < (5 - i - 1); j++)
{
cout << " ";
}
// 2.控制输出二维数组中的值,记得值和值之间有空格隔开
for (int k = 0; k <= i; k++)
{
cout << arr[i][k] << " ";
}
// 当前行输出完,再单独输出一个换行
cout << endl;
}
return 0;
}6、字符数组
①基本概念
字符数组本质上是存储字符的数组,每个元素占用 1 个字节( char 类型),通常用于存储字符串。字符串在字符数组中以空字符 ( \0 )结尾,表示字符串的结束。
示例:
// 数组 `str` 存储了字符串 `"Hello"` ,最后一个元素 `\0` 是隐式添加的终止符。
char str [ 6 ] = { 'H' , 'e' , 'l' , 'l' , 'o' , '\0' };
②定义初始化
★定义字符数组: char 数组名[常量表达式];
- 常量表达式 :数组的长度
- 示例: char name[20]; 定义一个可存储 19 个字符的数组(最后一个字符为 \0 )
★初始化方式 1 :逐个字符赋值
char name[6]={'h','e','l','l','o','\0'};
- 明确指定每个字符,包括终止符 \0 。
★初始化方式 2 :直接赋字符串
char name[]="Johon";
- 等价于 char name[5] = {'J', 'o', 'h', 'n', '\0'};
- 如果未指定大小,编译器会根据字符串长度自动分配空间
★初始化方式 3 :部分初始化
char name [ 10 ] = "John" ; // 剩余元素自动填充为 '\0'
数组长度大于初始化字符串长度时,剩余位置填充空字符 \0
初始化方式 4 :省略数组长度
char name [] = { 'J' , 'o' , 'h' , 'n' , '\0' }; // 自动计算长度
③数组输入
1 )使用 cin >> arr (直接输入)
行为 :
- 读取字符直到遇到空格、换行符或制表符
- 不会自动添加\0 (实际会添加,但可能导致缓冲区残留问题)
- 不推荐用于需要处理空格或换行的场景
示例 :
arr 的内容为 'h', 'e', 'l', 'l', 'o', '\0', ... (剩余位置未明确填充)最后一个字符是 \0 ,但可能残留未读取的换行符
2 )使用 cin.get(arr, 10)
行为 :
- 读取最多 9****个字符(留出 1 个位置给终止符 \0 )
- 如果输入的字符数少于 9,剩余位置会自动填充 \0
- 不会将换行符( \n )包含在数组中,但换行符会留在输入缓冲区中
- 自动在字符串末尾添加\0
示例 :
arr 的内容为 'h', 'e', 'l', 'l', 'o', '\0', '\0', '\0', '\0', '\0' (共 10 个字符)
最后一个字符是 \0
3 ) 使用 cin.getline(arr, 10)
行为 :
- 读取最多 9****个字符(留出 1 个位置给终止符 \0 )。
- 如果输入的字符数少于 9,剩余位置会自动填充 \0 。
- 会将换行符( \n )从缓冲区中移除(不会包含在数组中)。
- 自动在字符串末尾添加\0 。
示例 :
arr 内容为 'h', 'e', 'l', 'l', 'o', '\0', '\0', '\0', '\0', '\0' (共 10 个字符)
最后一个字符是 \0
关键点总结
| 输入方式 | 是否自动添加 \0 |
换行符处理 | 剩余位置填充 |
|---|---|---|---|
cin.get(arr, 10) |
是 | 留在缓冲区 | 自动填充 \0 |
cin.getline(arr, 10) |
是 | 从缓冲区移除 | 自动填充 \0 |
cin >> arr |
是 | 留在缓冲区(可能引发问题) | 未明确填充 |
结论
- 通过 cin.get(arr, 10) 或 cin.getline(arr, 10) 赋值后,字符数组 arr[10] 的最后一个字符会是 \0 ,确保字符串正确终止
- 推荐使用cin.getline() ,因为它会自动处理换行符,避免缓冲区残留
④处理函数
C++ 提供了 <cstring> 头文件中的标准库函数,用于操作字符数组:
| 函数 | 功能 |
|---|---|
strcpy(dest, src) |
复制字符串 src 到 dest |
strlen(str) |
返回字符串 str 的长度(不包含 \0) |
strcmp(str1, str2) |
比较两个字符串,返回 0 表示相等;str1>str2 返回正整数;str1<str2 返回负整数。 |
strcat(dest, src) |
将 src 追加到 dest 的末尾 |
示例:
cpp
#include <iostream>
#include <cstring>
using namespace std;
int main() {
char str1[20] = "Hello";
char str2[] = "World";
strcpy(str1, str2); // str1 = "World"
cout << "str1: " << str1 << endl;
cout << "Length: " << strlen(str1) << endl; // 输出 5
cout << "Compare: " << strcmp(str1, str2) << endl; // 输出 0
strcat(str1, "!"); // str1 = "World!"
cout << str1 << endl;
return 0;
}⑤常见问题
1 )忘记添加终止符 \0
- 若未手动添加 \0 ,字符串函数(如 strlen 、 strcpy )会继续读取内存,导致未定义行为。
- 正确做法
2 )缓冲区溢出
- 若输入字符串长度超过数组容量,会导致数据溢出,破坏内存
- 解决方法
3 )字符数组与字符串的区别
- 字符数组:固定大小的数组,存储字符序列
- 字符串:动态对象(如 std::string ),可自动调整大小
- 建议:现代 C++ 推荐使用 std::string 替代字符数组,避免手动管理内存
⑥使用二维数组存储多个字符串
char names [ 3 ][ 20 ] = {
"Alice" ,
"Bob" ,
"Charlie" };
- names 是一个 3 行、20 列的二维字符数组,可存储 3 个字符串(每个最多 19 个字符)。
遍历二维字符数组
for ( int i = 0 ; i < 3 ; ++ i )
{
cout << names [ i ] << endl ;
}
7、总结
| 特性 | 描述 |
|---|---|
| 基本用途 | 存储和处理字符串 |
| 终止符 | 字符串以 \0 结尾 |
| 输入输出 | 使用 cin(限于无空格字符串)或 cin.get()/getline() |
| 常用函数 | strcpy, strlen, strcmp, strcat(需包含 <cstring>) |
| 注意事项 | 避免缓冲区溢出,确保终止符存在 |
| 替代方案 | 使用 std::string 简化操作 |
8、字符串类
- 用字符数组来存放字符串并不是最理想和最安全的方法,C++提供了一种新的数据类型:字符串类型 string ,在使用方法上,它和 char、int 类型一样,可以用来定义变量,例如: string str;
- 实际上, string 并不是 C++语言本身具有的基本类型,它是在 C++标准库中声明的一个字符串类,用这种类可以定义对象,每一个字符串变量都是string 类的一个对象。
|----------|-----------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------|
| | 内容 | 注意 |
| 定义格式 | string str1; 定义字符串对象 string str2 = "hello"; 定义对象并初始化 | 要使用 string 类,需要添加头文件 #include <string> ,注意不 是 <cstring>或<string.h> 。 |
| 赋值 | 定义字符串变量后,可以用字符串常量给它赋值,例如: str1 = "briup"; 也可以用一个字符串变量给另一个字符串变量赋值,例如: str2 = str1; | 在定义字符串变量时不需指定长度,其长度会随其中的字符串长度而改 变。 |
可以对字符串变量中某一字符进行操作,如:
string str = "Then" ;
str [ 2 ] = 'a' ;
// 结果为: Than
cout << "str: " << str << endl ;
输入: cin >> str1 ; // 遇到空白字符,录入结束
字符串运算:
字符串变量可以借助 = + == != > >= < <= 直接进行运算。
案例: string s1 = "hello" ;
string s2 = "world" ;
string s3 = s1 + " " + s2 ;
cout << "s3: " << s3 << endl ; // 输出: "hello world"