一、概念
在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
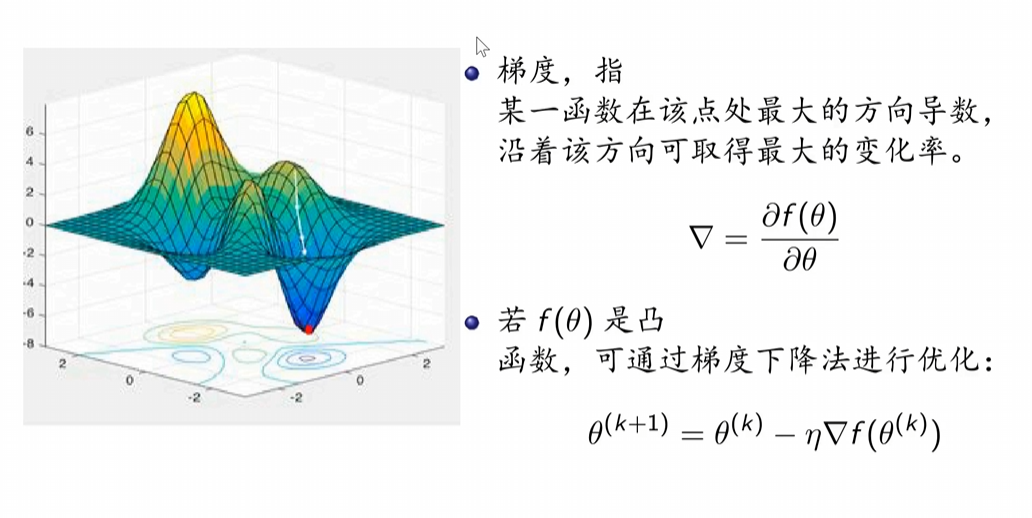
梯度向量的意义
从几何意义上讲，就是函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x0,y0)，沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x0, ∂f/∂y0)T的方向，梯度减少最快，也就是更加容易找到函数的最小值。
梯度下降与梯度上升
在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。反过来，求解损失函数的最大值，就用梯度上升法来迭代了。
梯度下降法相关概念
- 步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。
- 特征（feature）：指的是样本中输入部分，比如2个单特征的样本（x(0),y(0)）,（x(1),y(1)）,则第一个样本特征为x(0)，第一个样本输出为y(0)。
- 假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数。
- 损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。
二、详细算法
2.1代数法梯度下降
假设函数设为，则损失函数为
=
2.2算法推导过程
2.3梯度下降举例
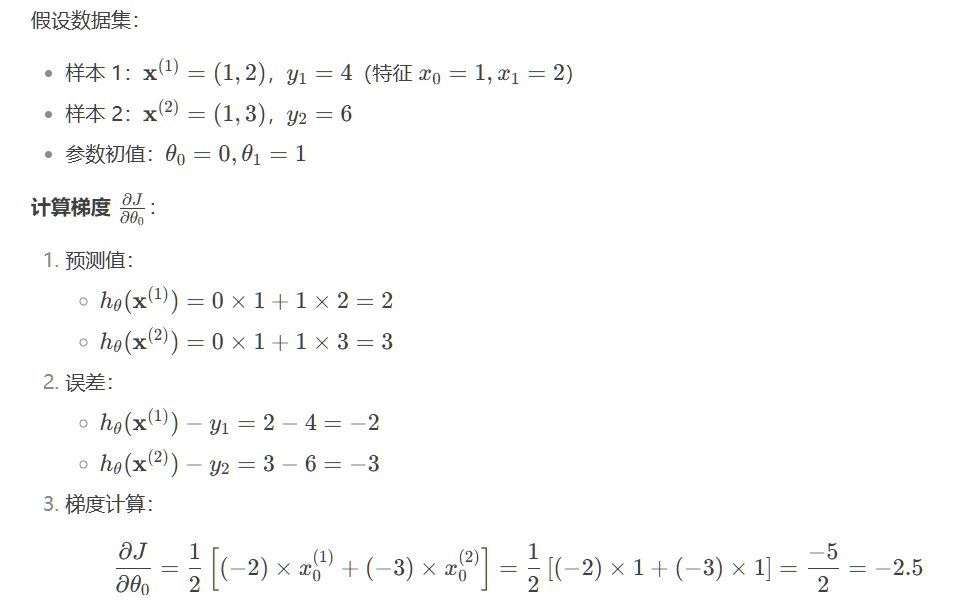
2.4梯度下降的算法调优
梯度下降更新公式：
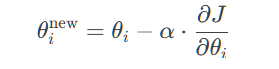
其中 α是学习率。
物理意义 ：梯度方向指向损失函数增长最快的方向，负梯度方向指向损失下降最快的方向。
- 算法的步长选择。步长实际上取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。
- 算法参数的初始值选择。 初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
- 归一化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化，也就是对于每个特征x，求出它的期望
和标准差std(x)，然后转化为：
参考文章：梯度下降（Gradient Descent）小结 - 刘建平Pinard - 博客园
https://www.cnblogs.com/pinard/p/5970503.html