位置编码RoPE介绍及其优化

绝对位置编码

传统的BERT中的实现方法，假设模型最大输出长度是512，向量纬度是768，需要先初始化一个512*768的位置编码矩阵。在每个位置，将位置编码直接加到token向量上。

问题：

不具备长度外推性。

正弦曲线(Sinusoidal)位置编码PE

是谷歌在Transformer中提出的绝对位置编码， 计算公式如下：

<math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( k , 2 i ) = s i n ( k 1000 0 2 i d ) P E ( k , 2 i + 1 ) = c o s ( k 1000 0 2 i d ) PE(k,2i) = sin(\frac{k}{10000^{\frac{2i}{d}}}) \\ PE(k,2i+1) = cos(\frac{k}{10000^{\frac{2i}{d}}}) </math>PE(k,2i)=sin(10000d2ik)PE(k,2i+1)=cos(10000d2ik)

其中，d表示向量纬度，k表示第k个位置，2i和2i+1表示位置向量的分量索引，如 <math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( k , 2 i ) PE(k,2i) </math>PE(k,2i)表示位置k向量第2i个分量。

正弦曲线位置编码每个分量都是正弦或者余弦函数，具有周期性 。如下图，每个分量都有周期性，而且越靠后的分量，波长越大，频率越低。

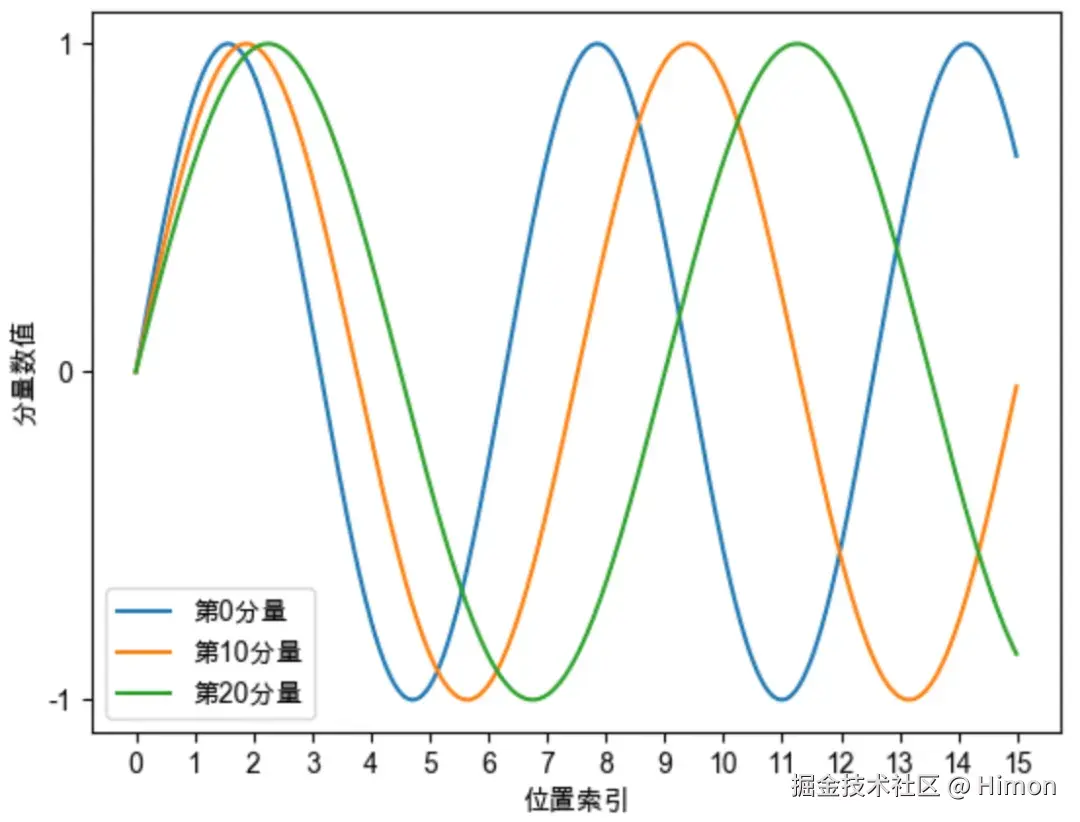
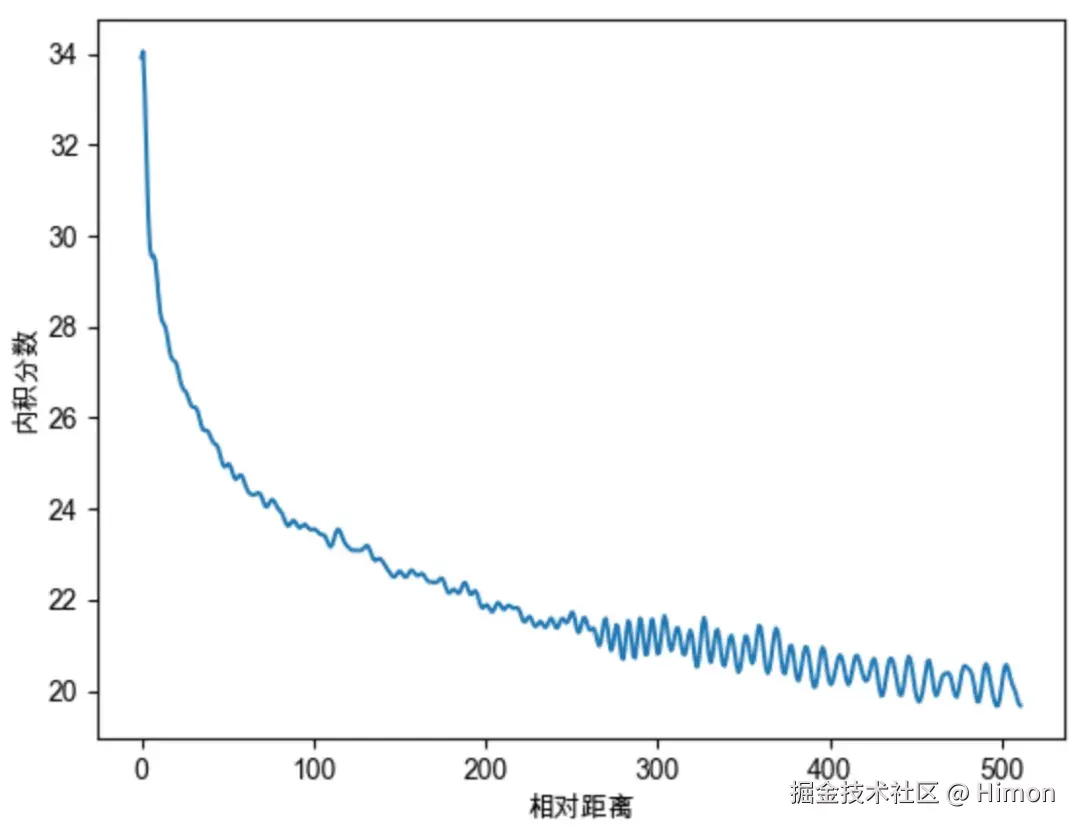
正弦曲线位置编码还具有远程衰减的性质：对两个相同的词向量，如果他们之间的距离越近，相对位置就越小，则他们的内积分数就越高，反之越小。

代码实现：

ini 复制代码

  class SinPositionEncoding(nn.Module):
      def __init__(self, max_sequence_length, d_model, base=10000):
          super().__init__()
          self.max_sequence_length = max_sequence_length
          self.d_model = d_model
          self.base = base

      def forward(self):
          pe = torch.zeros(self.max_sequence_length, self.d_model, dtype=torch.float)  # size(max_sequence_length, d_model)
          exp_1 = torch.arange(self.d_model // 2, dtype=torch.float)  # 初始化一半维度，sin位置编码的维度被分为了两部分
          exp_value = exp_1 / (self.d_model / 2)

          alpha = 1 / (self.base ** exp_value)  # size(dmodel/2)
          out = torch.arange(self.max_sequence_length, dtype=torch.float)[:, None] @ alpha[None, :]  # size(max_sequence_length, d_model/2)
          print(out)
          embedding_sin = torch.sin(out)
          embedding_cos = torch.cos(out)
          print(embedding_sin)

          pe[:, 0::2] = embedding_sin  # 奇数位置设置为sin
          pe[:, 1::2] = embedding_cos  # 偶数位置设置为cos
          return pe

旋转位置编码RoPE

实现原理
- 前面的PE是绝对位置编码，模型只能感知每个词所处的绝对位置，而无法感知两个词语之间的相对位置。
- RoPE的出发点：通过绝对位置编码的方式实现相对位置编码。
- 我们需要定义一个位置编码函数，可以对词向量q添加绝对位置信息m，得到 <math xmlns="http://www.w3.org/1998/Math/MathML"> q m = f ( q , m ) q_m = f(q,m) </math>qm=f(q,m)
- RoPE希望 <math xmlns="http://www.w3.org/1998/Math/MathML"> q m q_m </math>qm和 <math xmlns="http://www.w3.org/1998/Math/MathML"> k n k_n </math>kn之间的点积能够带有相对位置信息(m-n)。
- 建模目标：找到一个函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) f(q,m) </math>f(q,m)，使得如下关系成立： <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) ⋅ f ( k , n ) = g ( q , k , m − n ) f(q,m)·f(k,n)=g(q,k,m-n) </math>f(q,m)⋅f(k,n)=g(q,k,m−n)
二维情况

实现方法：采用旋转矩阵 ，当一个二维向量左乘一个旋转矩阵时，该向量即可实现弧度为 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ的逆时针旋转。

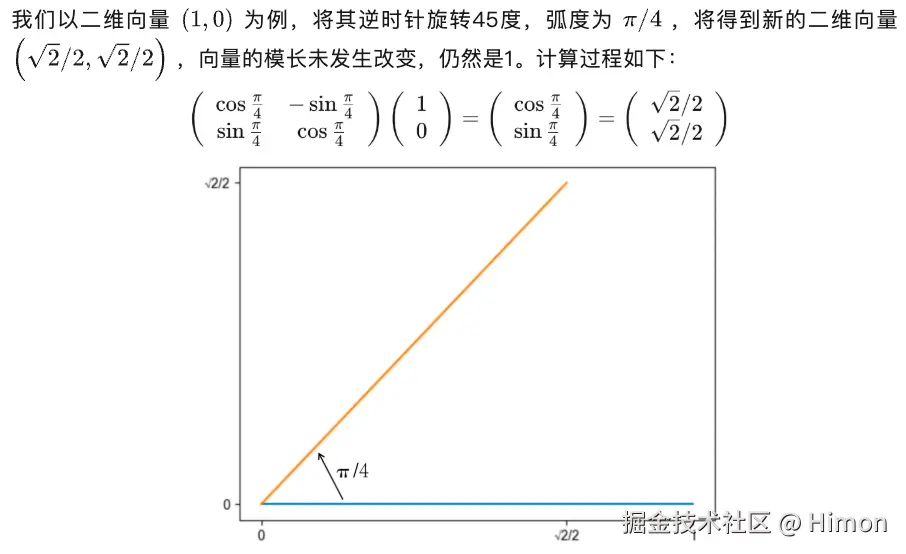
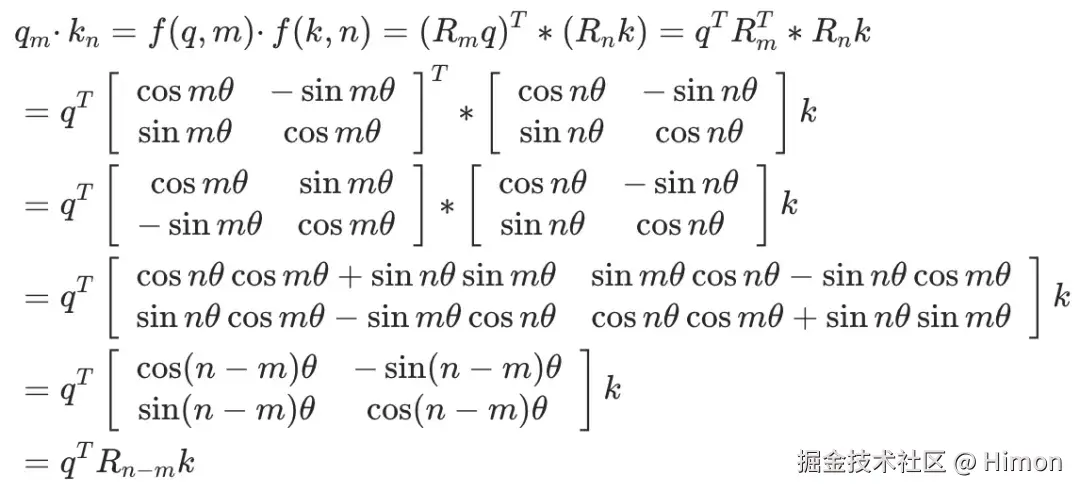
通过推理也可以得到(m-n)的信号量。

一个例子：

多维情况：

分而治之的思路：我们把高维向量，两两一组，分别旋转。

实现远程衰减性：

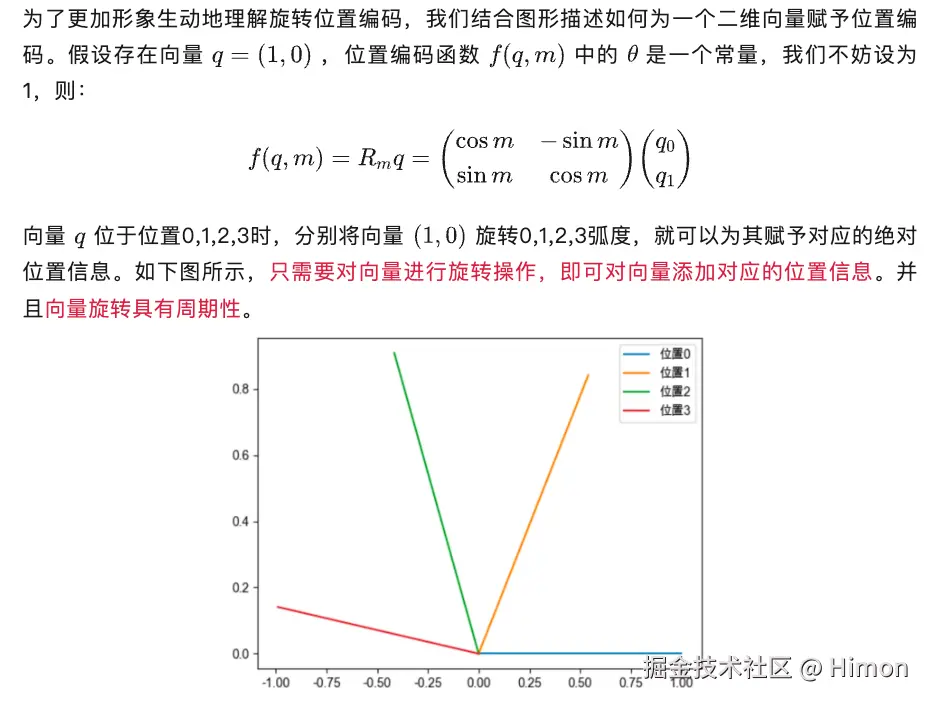
当我们把 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ设为1，随机初始化两个向量q和k，将q固定在0位置，k的位置从0开始逐渐增大，依次计算q和k之间的点积。下图中反映了点积的震荡图，最大的问题是：缺乏了远程衰减性！

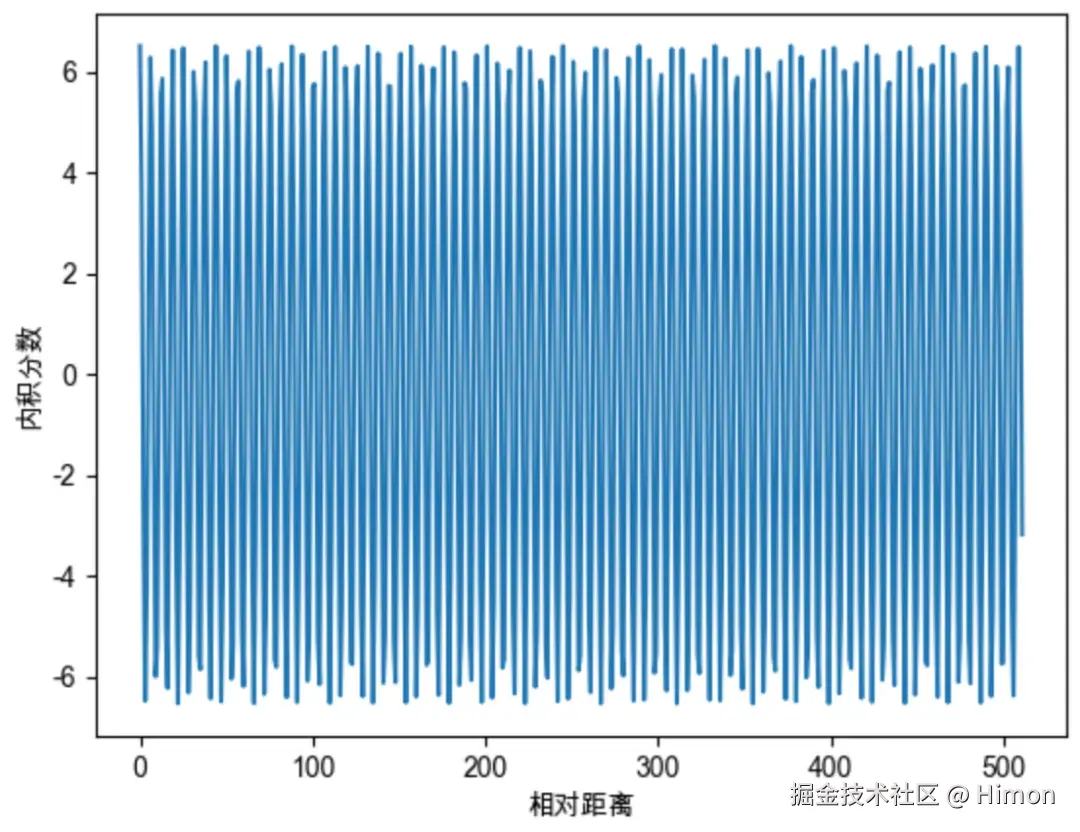
因此借鉴Sinusoidal位置编码，将每个分组的 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ设置为不同的常亮，从而引入远程衰减的性质：

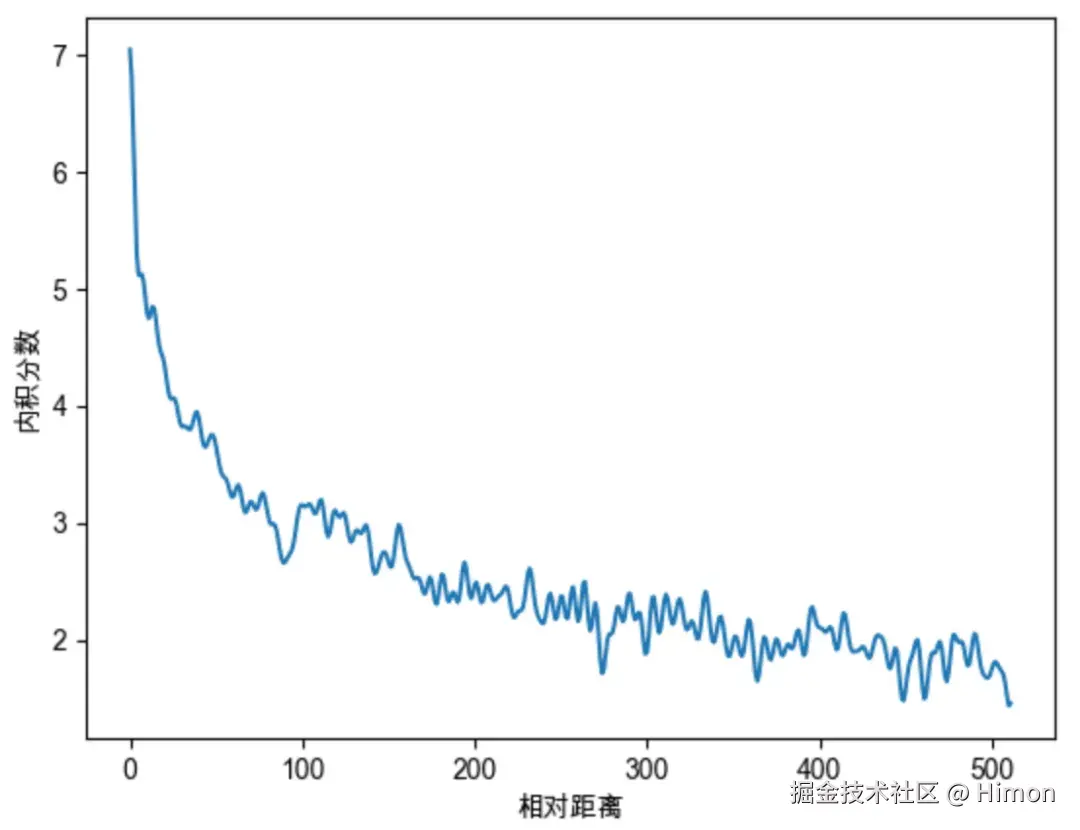
在原始的RoPE中，沿用了Sinusoidal的设置， <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ赋值为 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1000 0 − 2 i / d 10000^{-2i/d} </math>10000−2i/d，10000为base，实际上base的值对注意力远程衰减程度有影响：

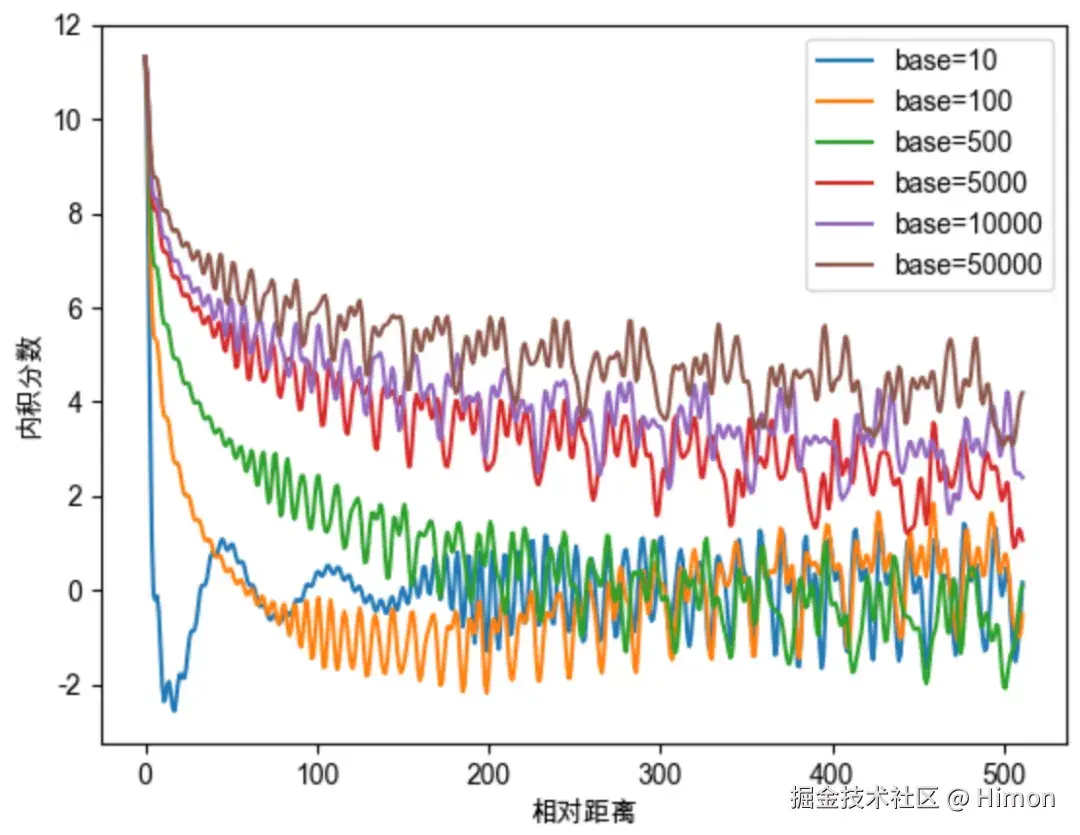
因此对base数值的研究，与大模型的外推能力有关系，如NTK感知插值、动态NTK感知插值等长度外推方法，本质上都是通过改变base值，影响每个位置对应的旋转角度，进而影响模型的位置编码信息。

周期性：

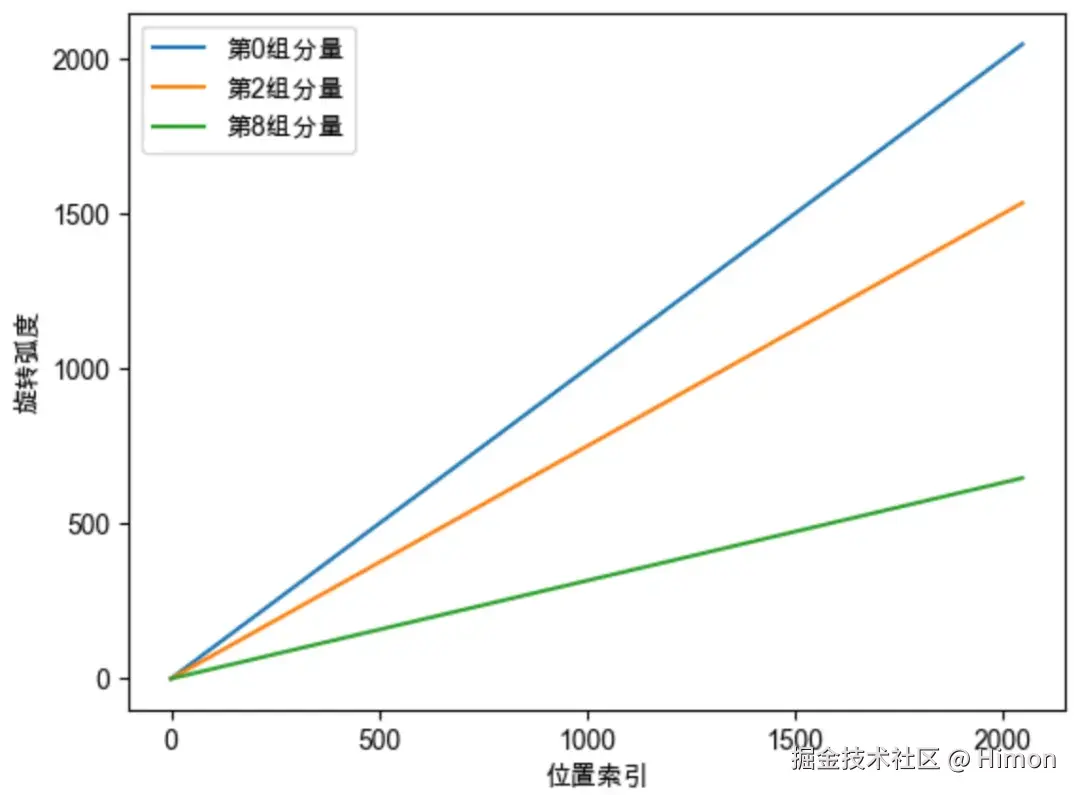
每组向量的旋转具有周期性，旋转一周的弧度是 <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 π 2\pi </math>2π，也就是转一圈又会回到原点，所有RoPE中的向量旋转就像时钟一样，具有周期性，如下图1。但是我们发现，越靠后的分组，向量的旋转速度越慢，如下图当位置位于500时，第0组分量已经旋转500弧度了，第8组分量才旋转158弧度。

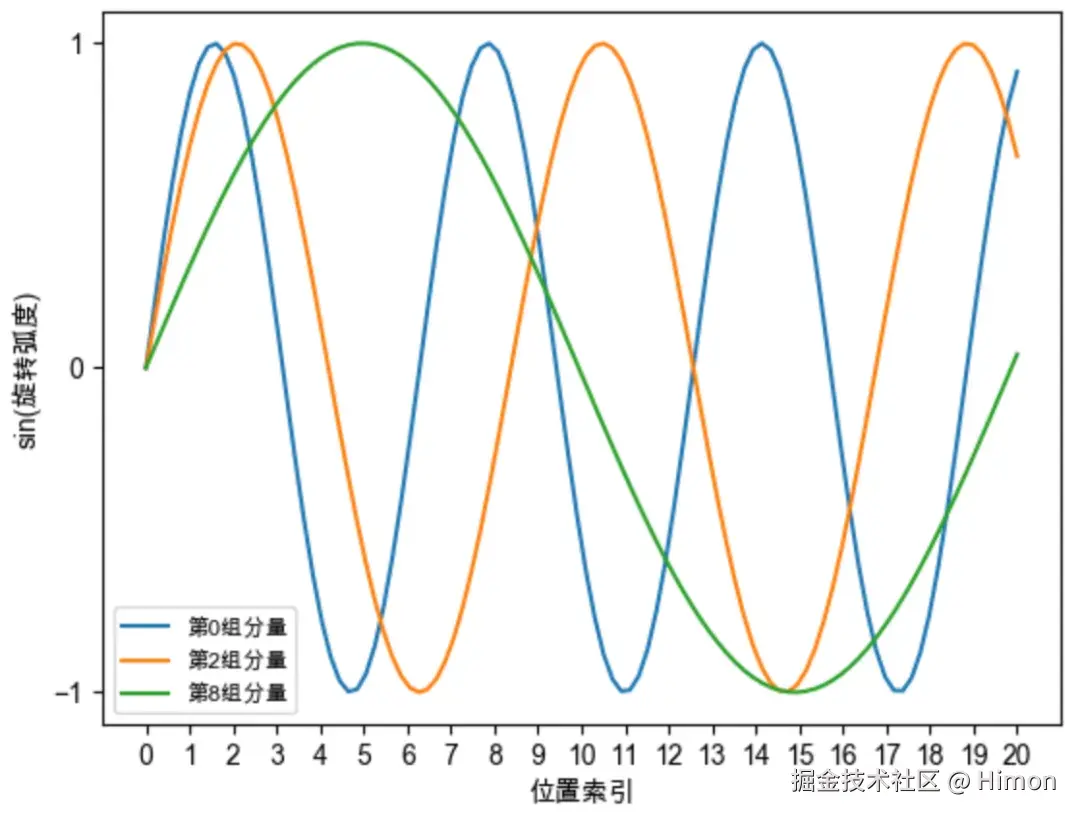
下面图2展示了上述旋转弧度对应的正弦函数，我们可以直观看到：越靠后的分组，它的旋转速度越慢，正弦函数的周期越大，频率越低。

参考：

图解RoPE旋转位置编码及其特性

RoPE的优化-位置插值法

做法很直接：缩小每个位置的旋转弧度，让向量旋转的慢一点，每个位置的旋转弧度变为原来的 <math xmlns="http://www.w3.org/1998/Math/MathML"> L L ′ \frac{L}{L'} </math>L′L ，长度扩大几倍，旋转弧度就缩小几倍。

问题点：

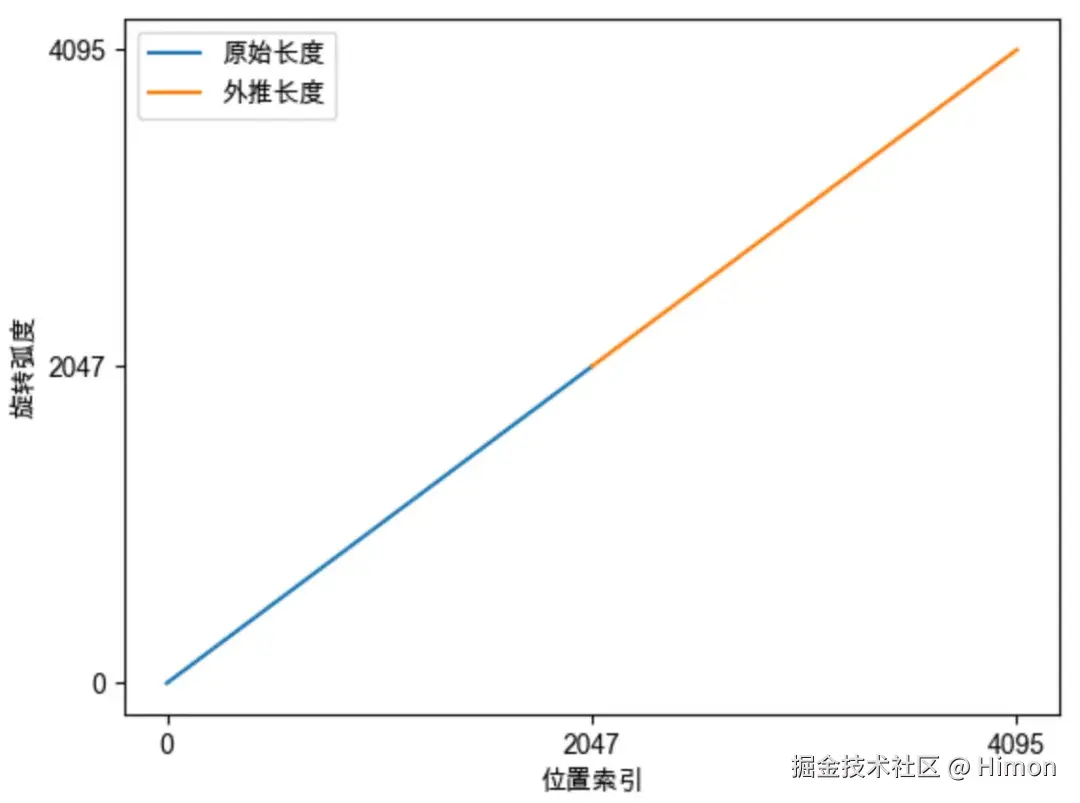
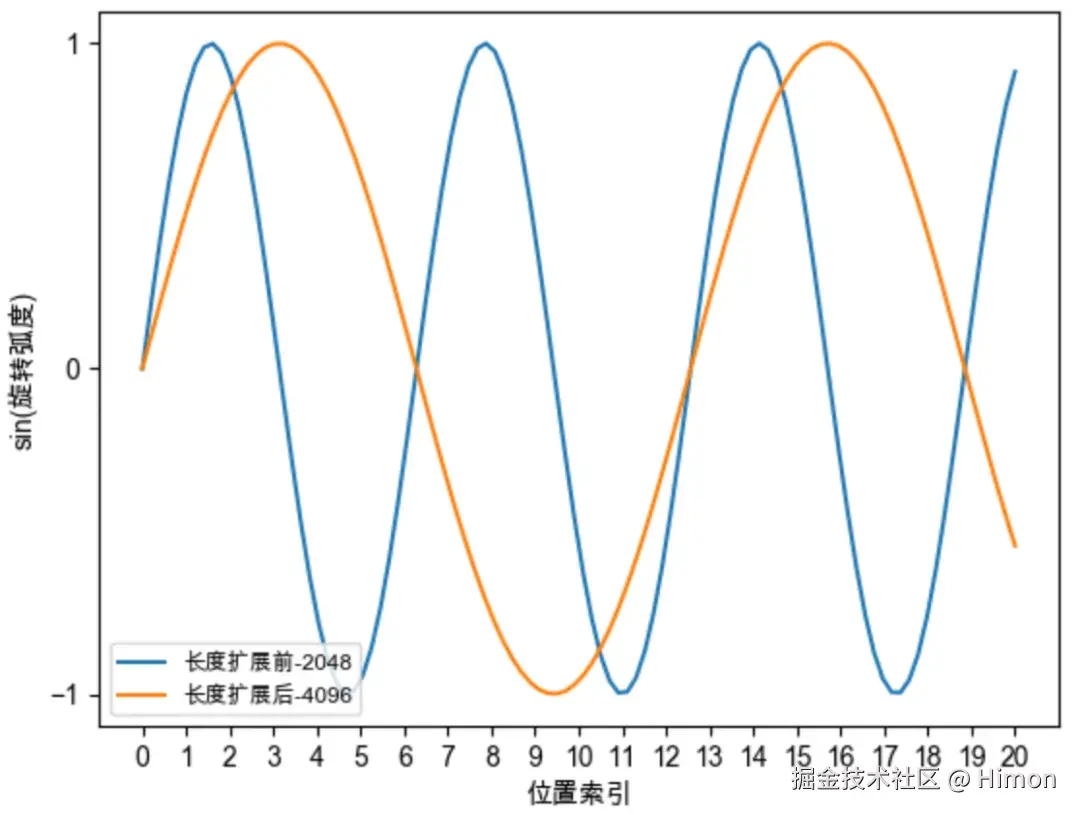
如图一，如果训练阶段sentence长度是[0,2048]，那么模型只见过[0,2048]的旋转弧度，没见过[2048,4096]的旋转弧度，模型难以理解新的旋转弧度，无法正确引入位置信息，导致模型性能下降。

优化效果
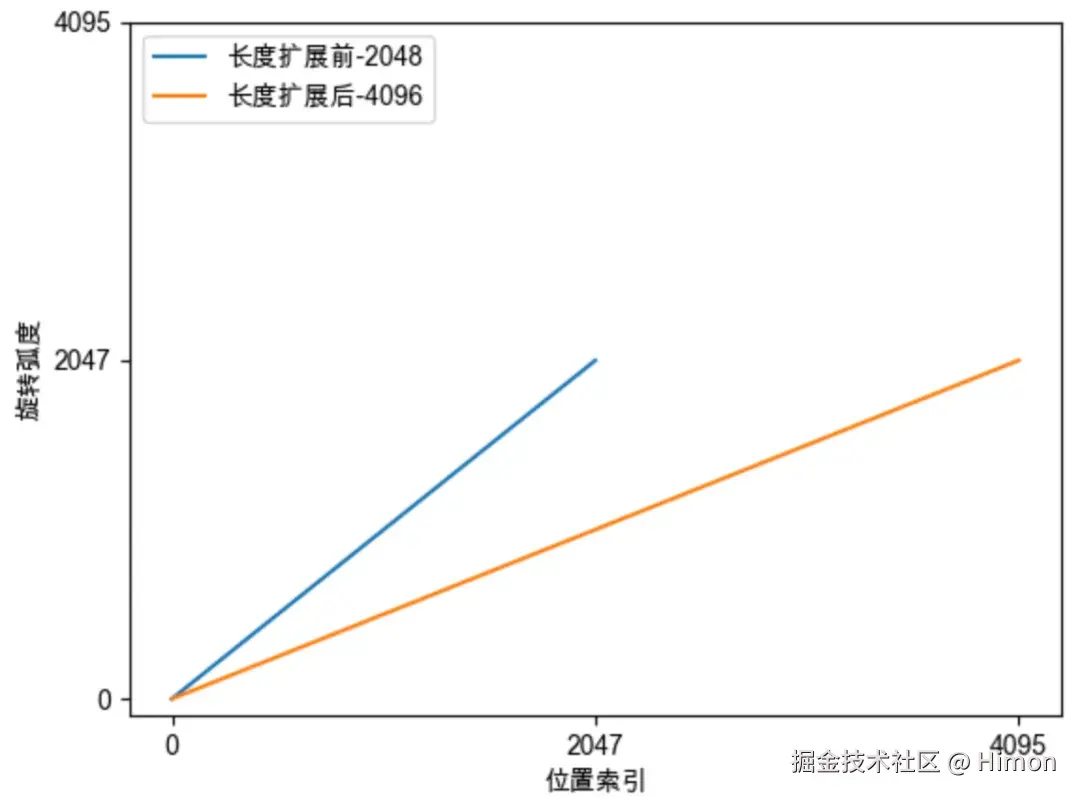
- 图二，展示了第0组分量旋转弧度的变化，位置插值法将0位置的旋转弧度变成原来的一半， 就可以看到[2048,4096]的旋转弧度了。
频率变化：

图3，经过位置插值之后，向量旋转变慢了，周期变大，频率变慢。

RoPE优化-NTK感知插值

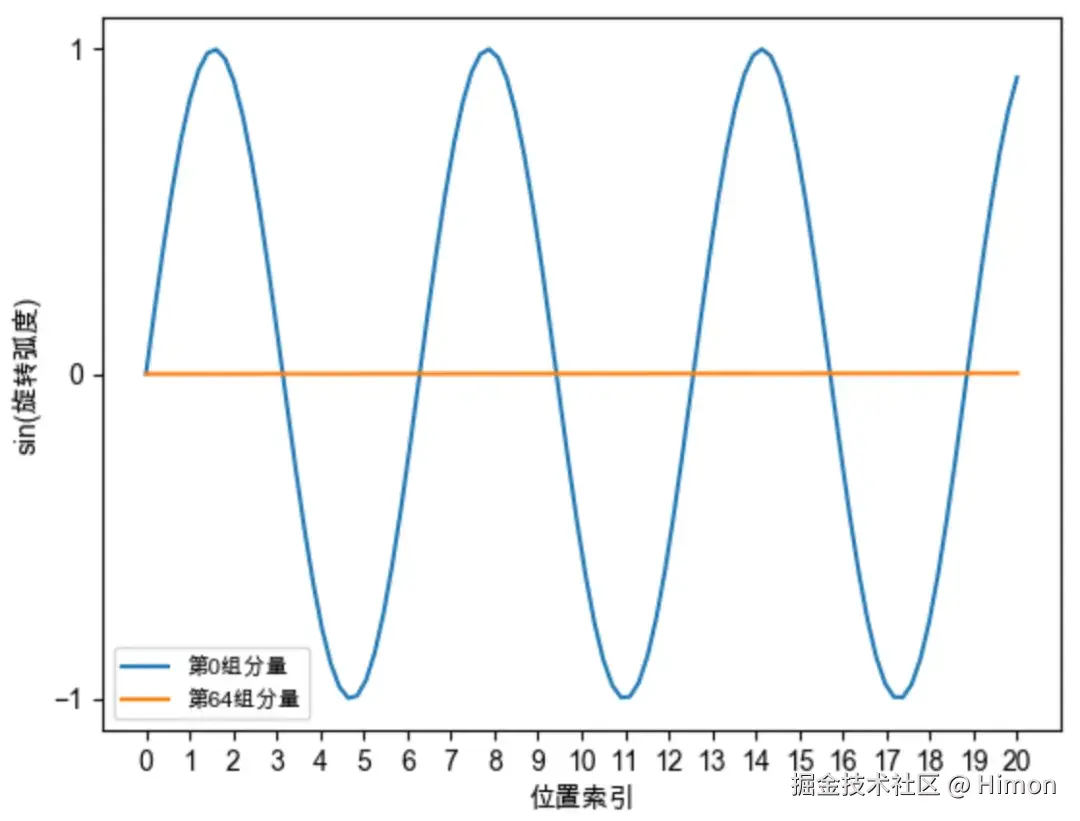
前面介绍过：位置越靠后的分量旋转速度越慢，频率越低，周期越长 ，如下图所示：对于第0组分量，在位置7的时候就已经旋转一周了，而对于第64组分量，在位置2047时，其旋转弧度约为0.2，仍然没有旋转1/4周。我们希望这些高频信息。

NTK感知插值做法：对base加一个缩放因子，进行放大 。保留高频信息，高频分量旋转速度降幅低，低频分量旋转速度降幅高；在高频部分进行外推，低频部分进行内插。

因此，我们将NTK感知插值有效的原因：

靠前的分组，在训练环节见过非常多的完整的旋转周期，位置信息得到充分训练，具有较强的外推能力。
靠后的分组，在训练环节无法见到完整的旋转周期，或者见到的非常少，训练不充分，外推性能弱。需要进行位置插值。

RoPE优化-NTK-by-parts Interpolation

做法：不改变高频部分，仅仅缩小低频部分的旋转弧度。

RoPE优化-动态NTK感知插值

做法：推理长度小于等于训练长度时，不进行插值，推理长度大于训练长度时，采用NTK动态插值法动态放大base。

RoPE优化-YaRN

问题：通过NTK办法，本质上都是减小旋转弧度，降低旋转速度 ，来达到长度外推的能力。这将导致两个位置之间的旋转弧度差距变小，词向量之间的距离比原来更大，点乘更大，这破坏了模型原始注意力分布。

参考：

详解基于调整RoPE旋转角度的大模型长度外推方法