目录
所有排序的实现皆以升序为例
1.直接选择排序
1.1直接选择排序的思想
直接选择排序的思想就是对数组进行多轮遍历 ,在每一轮遍历中,从当前未排序 部分的元素里选出最大值或最小值 ,然后依据排序要求,将该最大值或最小值与未排序部分的起始位置或末尾位置的元素 进行交换,从而逐步确定数组中各元素的最终位置,最终实现数组有序
1.2直接选择排序的代码逻辑
就是根据思想:遍历+筛选
1.3完整排序代码
1.3.1一次只选一个最值
void SelectSortUp1(int* a, int n){
for(int j = 0; j < n - 1; ++j){
int min = j;
for (int i = j + 1; i < n; ++i){
if (a[i] < a[min])
min = i;
}
Swap(&a[j], &a[min]);
}
}以升序为例,一次遍历(对未排序部分的遍历)选出的最小值放在未排序部分的起始位置
内层循环进行的是特定的某一次遍历的筛选过程
外层循环控制了每次遍历时的起始位置以及交换过程
1.3.2一次筛选出两个最值
void SelectSortUp2(int* a, int n){
int left = 0, right = n - 1;
while(left < right){
int min = left, max = left;
for (int i = left + 1; i <= right; ++i){
if (a[i] < a[min])
min = i;
if (a[i] > a[max])
max = i;
}
Swap(&a[min], &a[left]);
if (left == max)
max = min;
Swap(&a[max], &a[right]);
++left;
--right;
}
}对思想进行精进,一次遍历,选出未排序部分的最大和最小值,按需将其放在对应位置
left 、right控制的是未排序部分的区间大小
一次遍历选出最大最小值后,以升序为例,
最小值放在未排序部分的起始位置,最大值放在未排序部分的末尾
然后缩小区间
1.4直接选择排序的时间复杂度与空间复杂度
假设数组有N个元素,一次只选出一个最值,则最坏情况下,第一轮遍历需遍历N个元素,第二轮遍历序遍历N-1个元素.............第N-1轮遍历需遍历2个元素,遍历结束,遍历次数为((N+2)*(N-1))/2
所以时间复杂度为O(N^2)
一次筛选出两个最值,则最坏情况下,第一轮遍历大约需遍历N个元素,第二轮遍历需遍历N-2个元素.............一共约遍历N/2轮,遍历次数为 ((2+N)*N)/ 2,时间复杂度为O(N^2)
直接选择排序的变量个数固定,所有操作均在原数组上,所以空间复杂度为O(1)
2.堆排序
关于堆,可参考前两期博客 数据结构 之 【堆】 、堆的应用
2.1堆排序的思想
数组可以模拟完全二叉树,堆是一种完全二叉树,且具备选数的功能,那么
将数组持续变为堆,并对特定的堆选出最值,最终可实现数组有序
2.2堆排序的具体步骤
1.建堆:按需将所给数组变为大(小)堆 (建堆的具体步骤参考 堆的应用 这一期博客)
升序建大堆,降序建小堆
2.交换与调整:以升序为例,建成大堆后,将堆顶元素(为未排序部分的最大值)与末尾位置的元素进行交换,然后对末尾位置之前的所有元素进行向下调整操作,使其再次成为大堆,然后交换堆顶元素与未排序部分的末尾位置的元素,........循环进行调整与交换操作,直到未排序部分的元素个数为1为止
2.3堆排序图解

2.4完整排序代码
void AdjustDown(HpDateType* a, int n, int parent){
int child = parent * 2 + 1;
//有左孩子才进行调整
while (child < n)//n是节点个数{
//左孩子一个逻辑,右孩子一个逻辑,直接假设
//child是左右孩子中较大的一个孩子的下标
//注意右孩子的有无(防止越界访问与无效数据)
if (child + 1 < n && a[child] < a[child + 1]){
++child;
}
//与左右孩子中较大的一个孩子进行比较
if (a[parent] < a[child]){
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else break;
}
}
void HeapSortUp(int* a, int n){
//从第一个非叶子节点开始建堆
for (int i = (n - 2) / 2; i >= 0; --i){
AdjustDwon1(a, n, i);
}
//堆顶元素与末尾交换,并向下调整
//显然是循环
int end = n - 1;
while (end > 0){
Swap(&a[0], &a[end]);
AdjustDwon1(a, end, 0);
--end;
}
}通过逐步缩小堆的范围来排序数组
当堆中只剩一个元素时(即
end = 0),排序过程已完成, 所以 end > 0作为循环结束条件
2.5堆排序的时间复杂度与空间复杂度
堆排序的时间复杂度O(N*logN),可用最坏情况下的交换次数进行衡量
空间复杂度为O(1)
3.冒泡排序
3.1冒泡排序的思想
进行多轮遍历 ,每轮遍历中,依次比较相邻元素 ,若不符合目标顺序(升序则前大后小,降序则前小后大),就交换它们的位置。如此,每轮遍历会将当前未排序部分的最大(小)值"冒泡"到数组一端。当某一轮遍历无元素交换时,排序完成
3.2冒泡排序图解
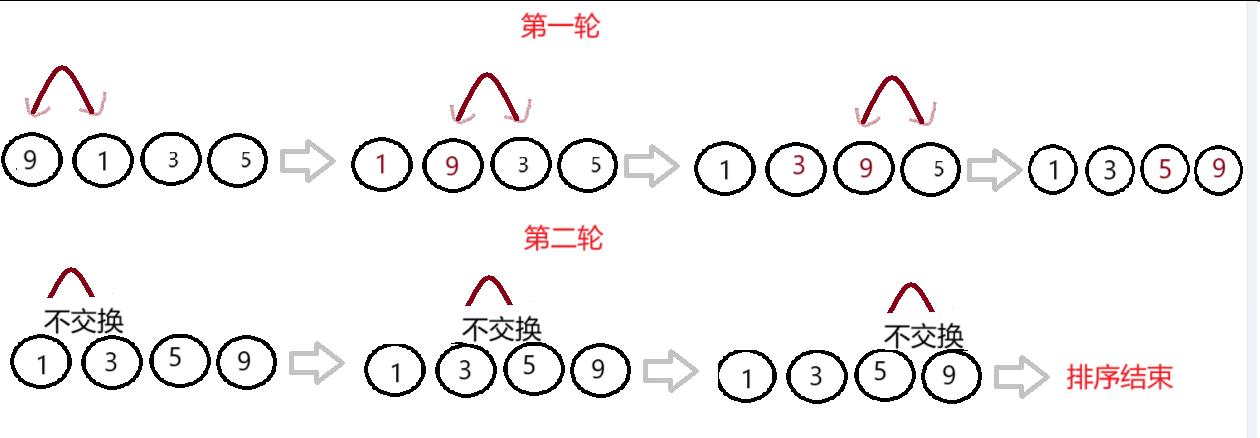
3.3单趟排序代码(一轮遍历进行的操作)
for (int j = 0; j < n - 1; ++j){
if (a[j] > a[j + 1]){
Swap(&a[j], &a[j + 1]);
}
}上述代码展示的是第一次遍历进行的操作,数组元素两两进行比较,j + 1 < n,所以 j < n - 1
因为是升序,前一个数比后一个数大就交换
3.4完整排序代码
void BubbleSortUp(int* a, int n){
//一趟只正确放好一个数
//n个数n - 1 趟
for(int i = 0; i < n - 1; ++i){
//经过一趟少一次比较
for (int j = 0; j < n - 1 - i; ++j){
if (a[j] > a[j + 1]){
Swap(&a[j], &a[j + 1]);
}
}
}
}冒泡排序遍历一轮可正确放好一个数组元素,则有n个数组元素的数组只需遍历n-1轮
冒泡排序遍历一轮可正确放好一个数组元素,那么遍历一轮可减少一次比较次数
小优化
内层循环未进行交换操作则证明数组有序,此时可终止循环,减少不必要的循环操作
void BubbleSortUp(int* a, int n){
//一趟只正确放好一个数
//n个数n - 1 趟
for(int i = 0; i < n - 1; ++i){
int flag = 0;
//经过一趟少一次比较
for (int j = 0; j < n - 1 - i; ++j){
if (a[j] > a[j + 1]){
Swap(&a[j], &a[j + 1]);
flag = 1;
}
}
if (!flag)
break;
}
}3.5冒泡排序的时间复杂度与空间复杂度
假设数组有N个元素,则最坏情况下,第一轮遍历需交换N-1次,第二轮遍历需交换N-2次,
.............第N-1轮遍历需交换1次,交换总次数为 ((N-1)*N) / 2,时间复杂度为O(N^2)
变量个数固定,所有操作均在原数组上,空间复杂度为O(1)