2. Java中常见的数据结构
简介
在Java中,数据结构一般可以分为两大类:线性数据结构和非线性数据结构
线性数据结构: 线性数据结构是指数据元素之间存在一对一的关系,即每个元素都有一个前驱和一个后继元素,形成线性序列。常见的线性数据结构包括:
数组(Array):一组连续存储的元素,通过索引进行访问。
链表(Linked List):由一系列节点组成,每个节点包含数据和指向下一个节点的引用。
栈(Stack):后进先出(LIFO)的数据结构,只允许在栈顶进行插入和删除操作。
队列(Queue):先进先出(FIFO)的数据结构,允许在队尾插入元素,在队首删除元素。
非线性数据结构: 非线性数据结构是指数据元素之间存在一对多或多对多的关系,形成非线性结构。常见的非线性数据结构包括:
树(Tree):由节点组成的层级结构,每个节点可以有零个或多个子节点。
散列表(Hash Table):使用哈希函数将键映射到存储位置的数据结构,通常用于实现集合和映射。
图(Graph):由节点(顶点)和边组成的集合,描述对象之间的关系,可以是有向图或无向图。
堆(Heap):特殊的树形数据结构,通常用于实现优先队列。
(1) 数组
在Java中,一些数据结构是直接暴露其底层实现的,而另一些数据结构则对其底层实现进行了封装。
直接暴露底层实现的数据结构: 例如 String[] 和 int[] 这种数组,它们的底层实现是直接暴露的,开发者可以直接访问和操作数组元素。这样的数据结构通常具有简单的接口和操作,易于理解和使用。
对底层实现进行封装的数据结构: 例如 ArrayList,它对数组进行了封装,并提供了一系列方法来操作数组。在使用 ArrayList 时,开发者无需关心其底层实现细节,只需调用相应的方法即可。这样的数据结构通常提供了更丰富的功能和更高的灵活性,但也可能会带来一些性能上的损耗。
数组这种数据结构最大的好处,就是可以根据下标进行操作,插入的时候可以根据下标直接插入到具体的位置,但与此同时,后面的元素就需要全部向后移动,需要移动的数据越多,就越慢。
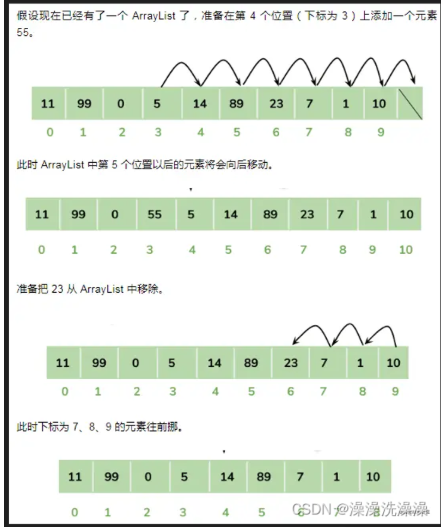
ArrayList 的常见操作的时间复杂度为 O(1) 或 O(n),具体取决于操作类型和操作位置。
-
添加元素(Add): 如果添加元素不涉及扩容操作,即 ArrayList 内部数组的容量足够,时间复杂度为 O(1)。但如果需要进行扩容,即当前元素数量达到容量上限时,需要将所有元素复制到新数组中,时间复杂度为 O(n)。
-
删除元素(Remove): 删除指定索引位置的元素,需要将该索引后面的所有元素向前移动一位,时间复杂度为 O(n)。如果删除的是末尾元素,时间复杂度为 O(1)。
-
随机访问(Get): 通过索引获取元素,时间复杂度为 O(1),因为 ArrayList 是基于数组实现的,可以通过索引直接访问数组元素。
-
搜索元素(Contains): 判断 ArrayList 中是否包含某个元素,时间复杂度为 O(n),因为需要遍历整个数组来搜索元素。
-
插入元素(Insert): 在指定索引位置插入元素,需要将该索引后面的所有元素向后移动一位,时间复杂度为 O(n)。如果插入的是末尾元素,时间复杂度为 O(1)。
(2) 链表
链表是一种非连续存储的数据结构,每个节点包含数据和指向下一个节点(单向链表)或者前一个节点和后一个节点(双向链表)的引用。这种相互链接的结构使得链表具有灵活性和高效性,在插入和删除操作时不需要像数组那样进行元素的移动。
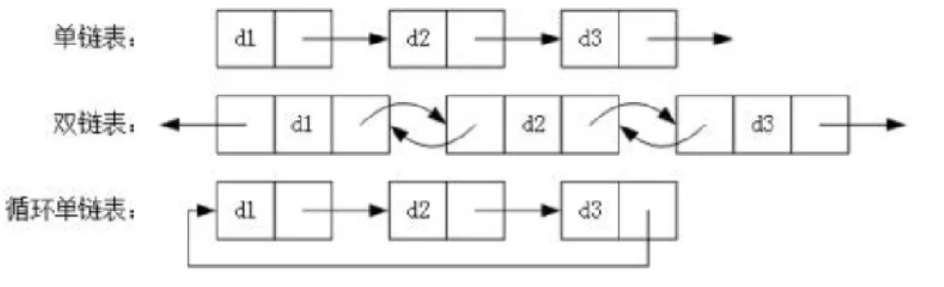
示例:
1. 单链表:
public class LinkNode<E>{//单链表结点泛型类
E data;//结点的数据域
LinkNode<E> next;//后继结点的指针域
public LinkNode(){//构造方法
next=null;
}
public LinkNode(E d){//重载构造方法
this.data=d;
this.next=null;
}
}
public class LinkListClass<E> {
//单链表泛型类
public LinkNode<E> head;//存放头结点
public LinkListClass() {//构造方法
this.head = new LinkNode<E>();//创建头结点
this.head.next = null;
}
public void CreateListF(E[] a){
LinkNode<E> s;
for (int i = 0;i < a.length;i++){
s = new LinkNode<E>(a[i]);
s.next = head.next;
head.next = s;
}
}
public void CreateListR(E[] a){
LinkNode<E> s,t = head;
for (int i=0;i<a.length;i++){
s = new LinkNode<E>(a[i]);
t.next = s;
t=s;
}
t.next = null;
}
//线性表的基本运算算法
private LinkNode<E> geti(int i){//返回序号为i的结点
LinkNode<E> p =head;
int j = -1;
while (j<i){
j++;
p=p.next;
}
return p;
}
//1)将元素e添加到线性表的末尾:Add(e)
public void Add(E e){
LinkNode<E> s = new LinkNode<E>(e);
LinkNode<E> p = head;
while (p.next!=null){ //查找尾结点p
p=p.next;
}
p.next=s;
}
//2)求线性表的长度
public int size(){
LinkNode<E> p = head;
int cnt = 0;
while (p.next!=null){
cnt++;
p=p.next;
}
return cnt;
}
//3)设置线性表的长度
public void Setsize(int nlen){
int len = size();
if (nlen<0||nlen>len){
throw new IllegalArgumentException("设置长度:n不在有效范围内");
}
if (nlen==len){
return;
}
LinkNode<E> p = geti(nlen-1);
p.next = null;
}
//4)求线性表中序号为i的元素
public E GetElem(int i){
int len = size();
if(i<0||i>len-1){
throw new IllegalArgumentException("查找:位置i不在有效范围内");
}
LinkNode<E> p = geti(i);
return (E)p.data;
}
//5)设置线性表中序号为i的元素
public void SetElem(int i,E e){
if (i<0||i>size()-1){
throw new IllegalArgumentException("设置:位置i不在有效范围内");
}
LinkNode<E> p = geti(i);
p.data = e;
}
//6)求线性表中第一个值为e的元素的逻辑序号
public int GetNo(E e){
int j = 0;
LinkNode<E> p = head.next;
while (p!=null&&!p.data.equals(e)){
j++;
p=p.next;
}
if (p==null){
return -1;
}else {
return j;
}
}
//7)将线性表中序号为i和序号为j的元素交换
public void swap(int i ,int j){
LinkNode<E> p = geti(i);
LinkNode<E> q = geti(j);
E tmp = p.data;
p.data = q.data;
q.data = tmp;
}
//8)在线性表中插入e作为第i个元素
public void Insert(int i ,E e){
if (i<0||i>size()){
throw new IllegalArgumentException("插入:位置i不在有效范围内");
}
LinkNode<E> s = new LinkNode<E>(e);
LinkNode<E> p = geti(i-1);
s.next = p.next;
p.next = s;
}
//9)在线性表中删除第i个数据元素
public void Delete(int i){
if (i<0||i>size()-1){
throw new IllegalArgumentException("删除:位置i不在有效范围内");
}
LinkNode<E> p = geti(i-1);
p.next=p.next.next;
}
@Override
public String toString() {
String ans = "";
LinkNode<E> p = head.next;
while (p!=null){
ans+=p.data+"";
p=p.next;
}
return ans;
}
}
2. 双链表
class DLinkNode<E> {
E data;
DLinkNode<E> prior; //区别:前驱结点指针
DLinkNode<E> next; //后继节点指针
public DLinkNode(){
prior=null;
next=null;
}
public DLinkNode(E d) {
data = d;
prior = null;
next = null;
}
}
public class DLinkListClass<E> {
DLinkNode<E> dhead;
public DLinkListClass(){
dhead=new DLinkNode<E>();
dhead.prior=null;
dhead.next=null;
}
//头插法:数组a建立双链表
public void CreateListF(E[] a){
DLinkNode<E> s;
for(int i=0;i<a.length;i++){
s=new DLinkNode<E>(a[i]);
s.next=dhead.next;
if(dhead.next!=null){
dhead.next.prior=s;
}
dhead.next=s;
s.prior=dhead;
}
}
//尾插法
public void CreateListR(E[] a){
DLinkNode<E> s,t;
t=dhead;
for(int i=0;i<a.length;i++){
s=new DLinkNode<E>(a[i]);
t.next=s;
s.prior=t; t=s;
}
t.next=null;
}
//尾插法
public void CreateListR(E[] a){
DLinkNode<E> s,t;
t=dhead;
for(int i=0;i<a.length;i++){
s=new DLinkNode<E>(a[i]);
t.next=s;
s.prior=t; t=s;
}
t.next=null;
}
public void Add(E e){
DLinkNode<E> s = new DLinkNode<E>(e);
DLinkNode<E> p = dhead;
while (p.next!=null){
p=p.next;
}
p.next=s;
}
public int size(){
DLinkNode<E> p = dhead;
int cnt = 0;
while (p.next!=null){
cnt++;
p=p.next;
}
return cnt;
}
private DLinkNode<E> geti(int i){
DLinkNode<E> p = dhead;
int j = -1;
while (j<i){
j++;
p=p.next;
}
return p;
}
public void Setsize(int nlen){
int len = size();
if (nlen<0||nlen>len){
throw new IllegalArgumentException("设置长度:n不在有效范围内");
}
if (nlen==len){
return;
}
DLinkNode<E> p = geti(nlen-1);
p.next=null;
}
public E GetElem(int i){
int len = size();
if (i<0||i>len-1){
throw new IllegalArgumentException("查找:位置i不在有效范围内");
}
DLinkNode<E> p = geti(i);
return (E)p.data;
}
public void SetElem(int i,E e){
if (i<0||i>size()-1){
throw new IllegalArgumentException("设置:位置i不在有效范围内");
}
DLinkNode<E> p = geti(i);
p.data=e;
}
public int GetNo(E e){
int j=0;
DLinkNode<E> p = dhead.next;
while (p!=null&&!p.data.equals(e)){
j++;
p=p.next;
}
if (p==null){
return -1;
}
else {
return j;
}
}
public void Insert(int i,E e){
if(i<0 || i>size()){
throw new IllegalArgumentException("插入:位置i不在有效范围内");
}
DLinkNode<E> s=new DLinkNode<E>(e);
DLinkNode<E> p=geti(i-1);
s.next=p.next;
if(p.next!=null){
p.next.prior=s;
}
p.next=s;
s.prior=p;
}
public void Delete(int i){
if(i<0 || i>size()-1){
throw new IllegalArgumentException("删除:位置i不在有效范围内");
}
DLinkNode<E> p=geti(i);
if(p.next!=null){
p.next.prior=p.prior;
}
p.prior.next=p.next;
}
public static void Delx(DLinkListClass<Integer> L,Integer x){
DLinkNode<Integer> p=L.dhead.next;
while(p!=null && p.data!=x){
p=p.next;
}
if(p!=null){
if(p.next!=null){
p.next.prior=p.prior;
}
p.prior.next=p.next;
}
}
3. 循环链表
public class CLinkListClass<E>{ //循环单链表泛型
LinkNode<E> head; //存放头结点
public CLinkListClass(){ //构造方法
head=new LinkNode<E>(); //创建头结点
head.next=head; //置为空的循环单链表
}
}
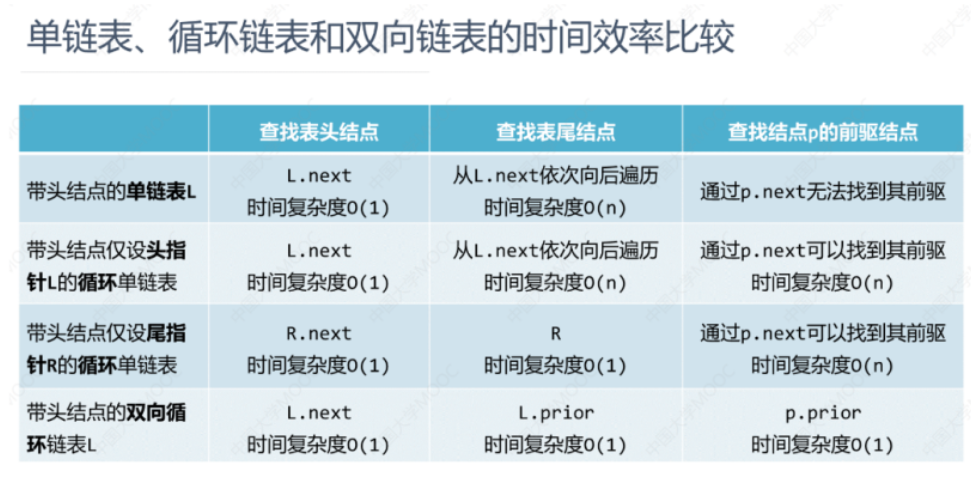
循环单链表的插入和删除节点操作与非循环单链表相同,所以两者的许多基本运算算法是相似的,主要区别如下:
1)初始只有头结点head,在循环单链表的构造方法中需要通过 head.next = head 语句置为空表。
2)循环单链表中涉及查找操作时需要修改表尾判断条件,例如:用 p 遍历时,尾节点满足的条件是 p.next ==head 而不是 p.next == null。
3)链表中没有空指针域。

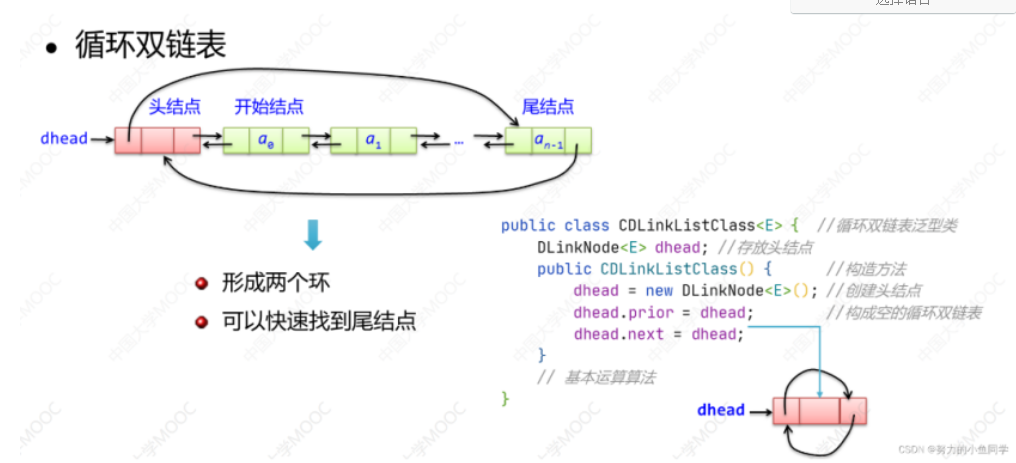
LinkedList 是链表的典型实现之一,它是由一系列节点组成的,每个节点包含数据和指向下一个节点的引用。LinkedList 的优点是插入和删除操作效率高,但随机访问效率较低,因为要从头节点开始遍历到目标位置。此外,LinkedList 还支持双向链表的实现,每个节点同时具有指向前一个节点和后一个节点的引用,进一步增强了灵活性。
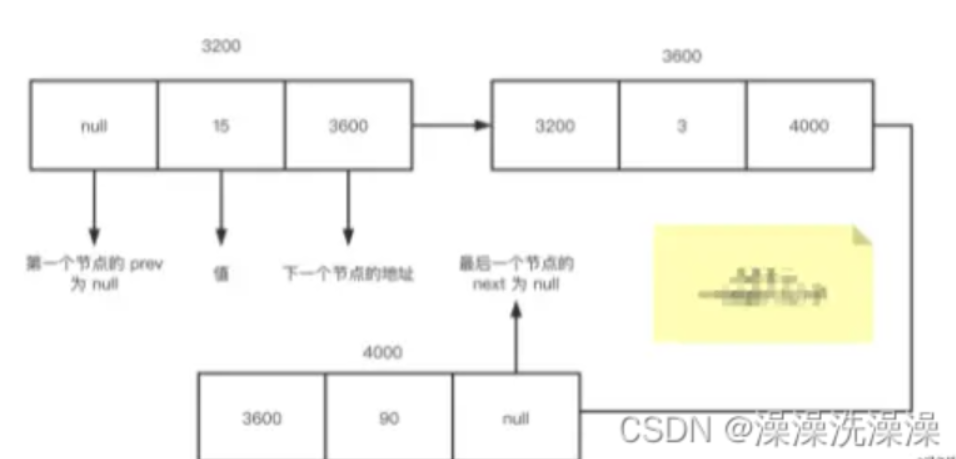
• 第一个节点由于没有前一个节点,所以 prev 为 null
• 最后一个节点由于没有后一个节点,所以 next 为 null
• 这是一个双向链表,每一个节点都由三部分组成,前后节点和值
相比ArrayList,LinkedList具有以下优势:
• 插入和删除操作效率高: 在链表中,插入和删除元素的效率不受集合大小的影响,因为只需要调整节点的指针,而不需要移动大量元素。而 ArrayList 在插入和删除操作时,需要移动数组中的元素,其效率受到集合大小的影响。
• 内存空间利用率高: LinkedList 的节点是动态分配的,不像 ArrayList 需要预先分配一定大小的数组空间,因此在内存空间利用率上更加灵活,不会出现过度分配或浪费的情况。
• 支持高效的头部和尾部操作: 在 LinkedList 中,头部和尾部操作(如添加、删除)的时间复杂度都是 O(1),而在 ArrayList 中,如果在头部进行添加或删除操作,需要将所有元素向后移动,时间复杂度为 O(n)。
• 支持更多的操作: LinkedList 支持更多的操作,如在任意位置插入或删除元素的操作,以及在迭代过程中删除元素等,这些操作在 ArrayList 中可能效率较低或者需要额外的操作。
LinkedList 在插入和删除操作频繁、需要高效的头部和尾部操作、以及对内存空间利用率要求较高的场景下,相比ArrayList 具有更大的优势。
示例代码:
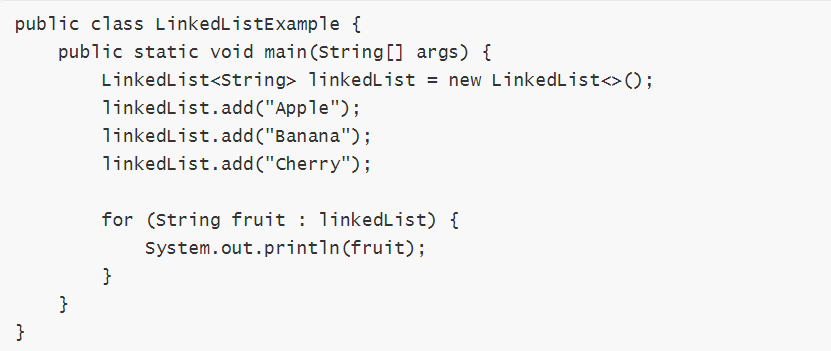
(3) 栈
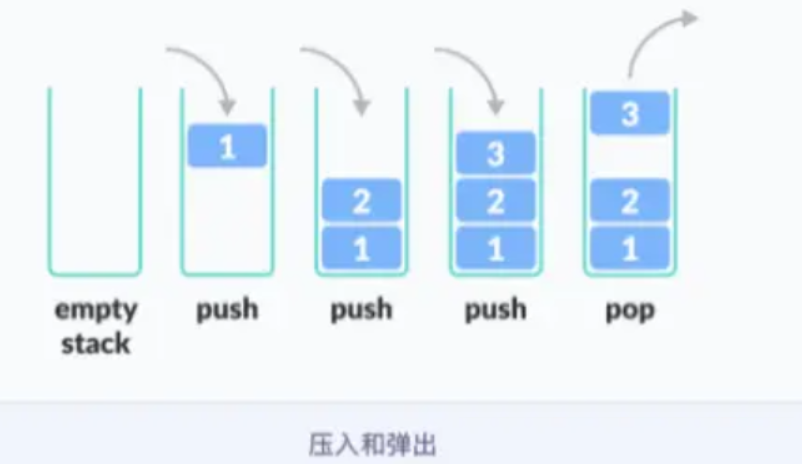
栈常被比喻为一摞盘子或者一堆书,遵循后进先出(LIFO)的原则。这意味着最后放入栈中的元素将被最先移除,而最先放入的元素将被最后移除。
对于栈这样一个数据结构来说,它有两个常见的动作:
• 入栈(Push): 将新的元素放入栈顶。新元素被添加到栈顶后,它将成为下一个被移除的元素,即栈顶元素。
• 出栈(Pop): 移除栈顶的元素并返回该元素的值。被移除的元素是最后一个被添加到栈中的元素,也是最后一个进栈的元素。
示例代码:

(4) 队列
队列是一种常见的数据结构,在Java中也有多种实现以满足不同的场景需求。队列的特点是只允许在队尾添加数据,而在队首移除数据,遵循先进先出(FIFO)的原则。
Java中常见的队列实现包括:
• LinkedList: Java 标准库中提供的 LinkedList 类实现了 Queue 接口,可以作为普通队列使用。
• ArrayDeque: ArrayDeque 类实现了双端队列(Deque)接口,可以作为普通队列使用,并且提供了高效的数组实现。
• PriorityQueue: 优先级队列实现了 Queue 接口,具有优先级的概念,可以按照元素的优先级顺序进行插入和删除操作。
• DelayQueue: 延时队列实现了 BlockingQueue 接口,用于存储实现了 Delayed 接口的元素,这些元素按照指定的延时时间从队列中移除。
• LinkedBlockingQueue 和 ArrayBlockingQueue: 这两个类实现了 BlockingQueue 接口,是线程安全的阻塞队列,可用于多线程环境下的生产者-消费者模式。
示例代码:

(5) 树
树是一种典型的非线性结构,它是由 n(n>0)个有限节点组成的一个具有层次关系的集合。之所以叫"树",是因为这种数据结构看起来就像是一个倒挂的树,只不过根在上,叶在下。树形数据结构有以下这些特点:
• 层次关系: 树是由n(n>0)个有限节点组成的集合,节点之间存在着层次关系,即从根节点到每个节点都存在一条唯一的路径。
• 根节点: 树有且仅有一个根节点,它位于树的顶部,是树中所有其他节点的起始点。
• 分支节点和叶节点: 除了根节点外,树中的每个节点都有且仅有一个父节点,但可以有零个或多个子节点。没有子节点的节点称为叶节点,也可以称为叶子节点。
• 子树: 每个节点都可以作为一个子树的根节点,包含该节点及其所有后代节点。
• 路径: 从树的根节点到任意节点都存在唯一的路径,路径的长度是经过的边的数量。
• 深度: 从根节点到某个节点的唯一路径的长度称为该节点的深度,根节点的深度为0。
• 高度: 树中任意节点的最大深度称为树的高度。
• 子树之间互不相交: 树中任意两个子树之间的节点都互不相交,即每个节点只能出现在一个子树中。
• 无环: 树中不存在环路,即不存在任何节点可以通过任意数量的边回到自身。
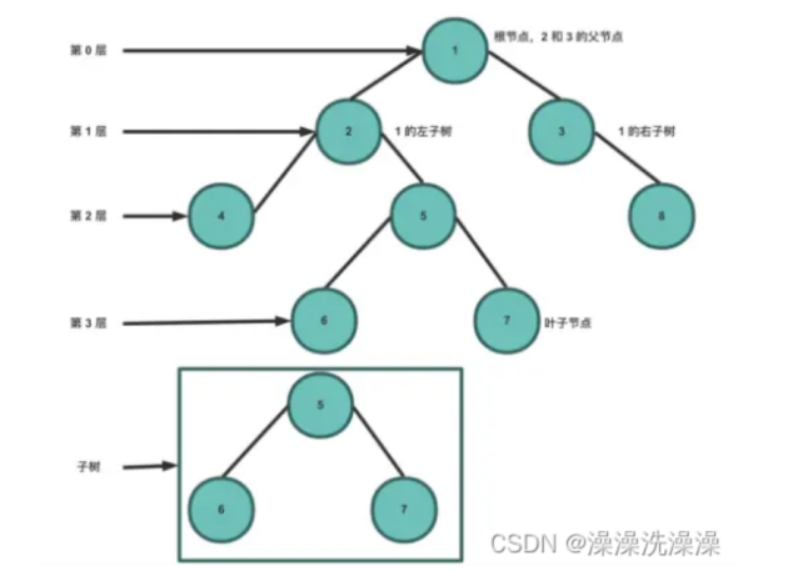
根节点是第 0 层,它的子节点是第 1 层,子节点的子节点为第 2 层,以此类推。
• 深度:是从根节点从上往下算起,根节点的深度为0,再往下就依次加1
• 高度:是从最底下算起,最底下为0,根节点的高度是最高的
树又可以细分为下面几种:
-
普通树:对子节点没有任何约束。
-
二叉树:每个节点最多含有两个子节点的树。 二叉树按照不同的表现形式又可以分为多种
2.1 普通二叉树:每个子节点的父节点不一定有两个子节点的二叉树。
2.2 完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第 d 层外,其它各层的节点数目均已达最大值,且第 d 层所有节点从左向右连续地紧密排列。
2.3 满二叉树:一颗每一层的节点数都达到了最大值的二叉树。有两种表现形式,第一种,像下图这样(每一层都是满的),满足每一层的节点数都达到了最大值 2。
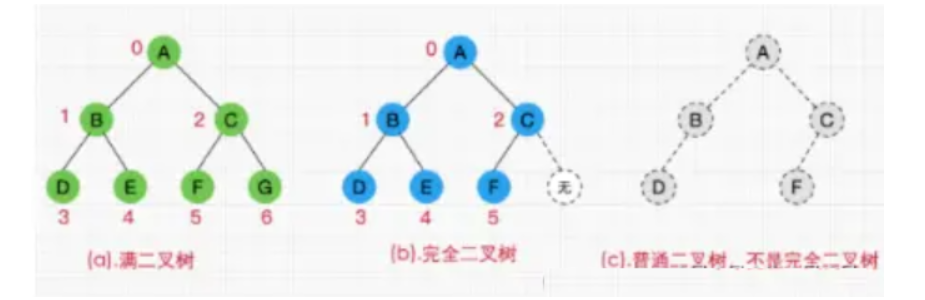
2.4 顺序存储(数组)
所谓的顺序存储,指的是使用数组存储的二叉树。
我们在使用数组存储时,会按照层级顺序把二叉树的结点放到数组中对应的位置上。如果某一个结点的左子结点或右子结点空缺,则数组的相应位置也要空出来。对于一个稀疏的二叉树(子结点不满)来说,用顺序存储是非常浪费空间的。所以说完全二叉树才适合使用顺序表存储。当顺序存储普通二叉树时,需要提前将普通二叉树转化为完全二叉树。
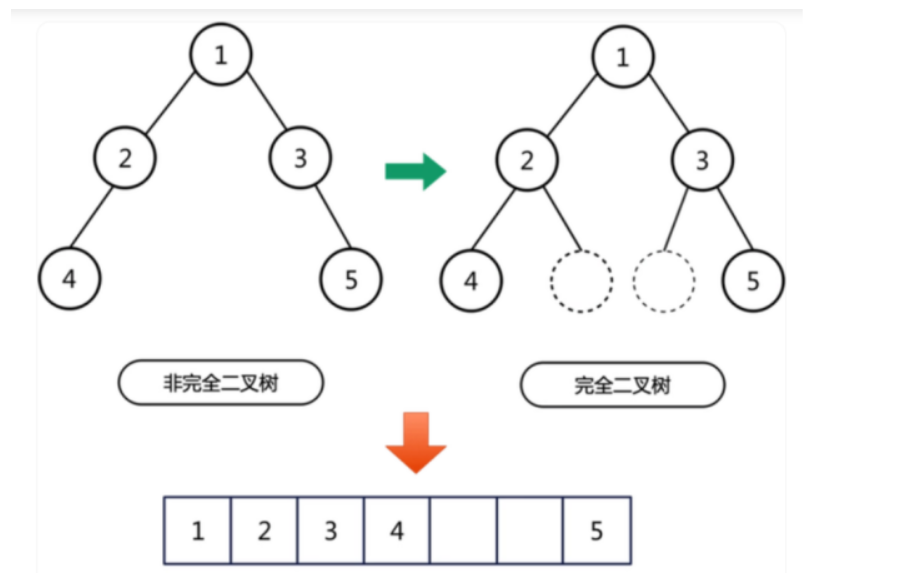
如上图所示,给定的二叉树是一棵普通的二叉树。若使用数组进行存储,首先需要将该二叉树补充调整为一棵完全二叉树如上右图所示,需要添加的两个结点使用虚线表示,然后再使用数组存储该完全二叉树。
由此,我们也能进一步理解:若使用数组存储普通二叉树,往往会浪费存储空间。
2.5 二叉树链式存储(链表)
我们推荐大家使用链表对二叉树进行存储。链式存储二叉树,其结点结构与双向循环链表一致,每一个结点包含三个部分:存储数据的data变量、指向左子结点的left指针、指向右子结点的right指针,这样的链表称为二叉链表。如下图所示:
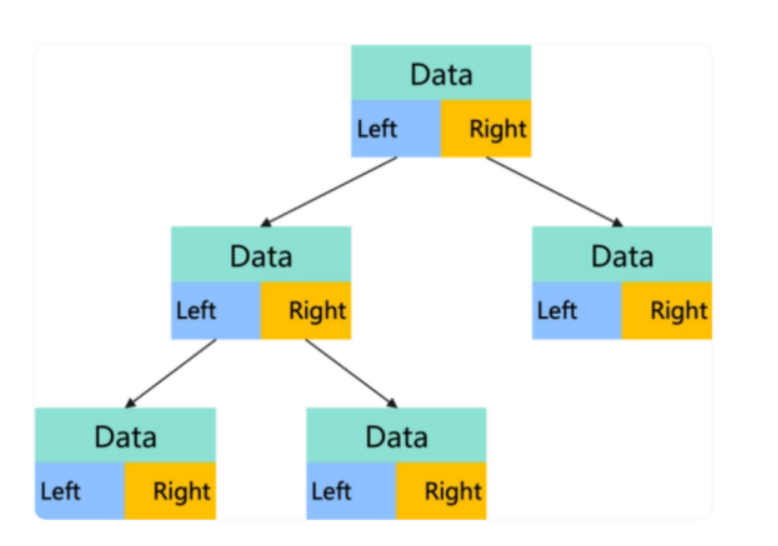
2.6 二叉树的创建(Java)
创建一个 TreeNode 类代表节点 TreeNode 代表节点,每个 TreeNode 对象表示一个节点,left 存放的是左子树,right 存放的是右子树,val 存放的是该节点的值。

2.7 二叉树的遍历
以下图为例说明二叉树的遍历
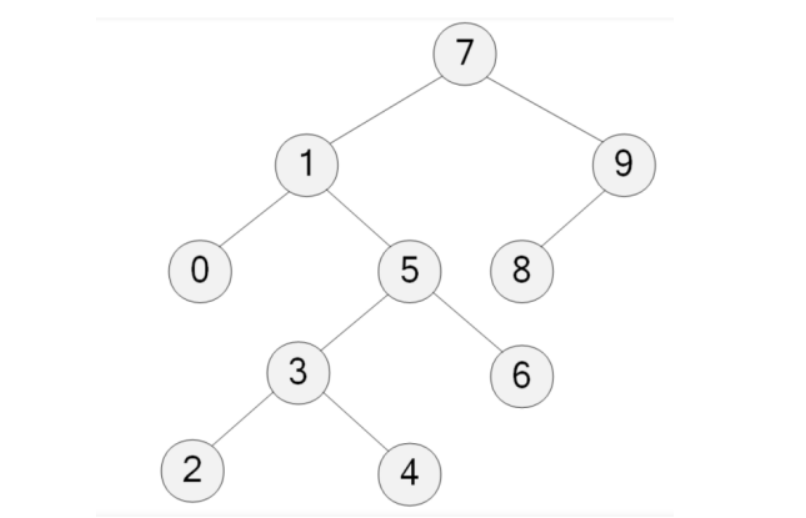
2.7.1 二叉树的先序遍历(深度优先遍历)
先序遍历为根节点、左子树节点、右子树节点的顺序遍历,采用递归的方式。
如第一节图中的二叉搜索树所示的二叉树先序遍历为:7 1 0 5 3 2 4 6 9 8
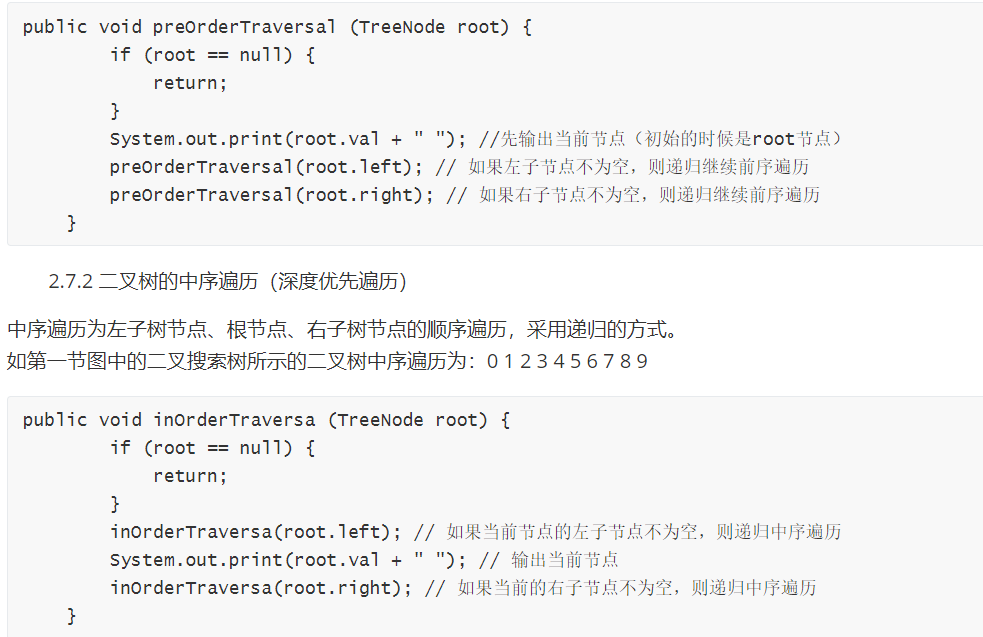
2.7.3 二叉树的后序遍历(深度优先遍历)
后序遍历为左子树节点、右子树节点、根节点的顺序遍历,采用递归的方式。 如第一节图中的二叉搜索树所示的二叉树后序遍历为:0 2 4 3 6 5 1 8 9 7

2.7.4 二叉树的层次遍历(广度优先遍历)
层次遍历,即广度优先遍历,采用队列的方式实现。 如第一节图中的二叉搜索树所示的二叉树层次遍历为:7 1 9 0 5 8 3 6 2 4

- 二叉查找树:英文名叫 Binary Search Tree,即 BST,需要满足:1、任意节点的左子树不空,左子树上所有节点的值均小于它的根节点的值。2、任意节点的右子树不空,右子树上所有节点的值均大于它的根节点的值。3、任意节点的左、右子树也分别为二叉查找树
下图即为一个二叉查找树:
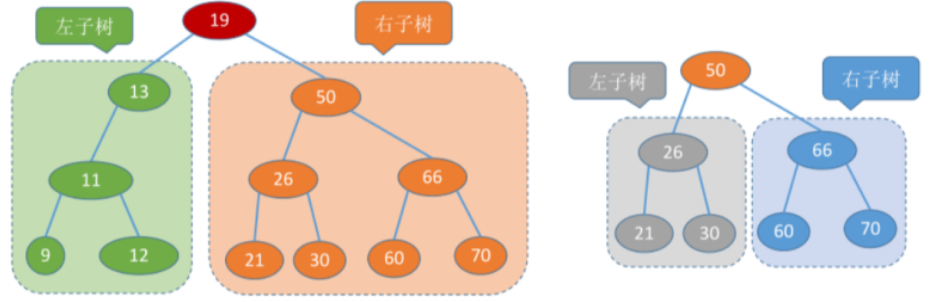
示例:
/**
* search 搜索的意思
*
* @param val
* @return
*/
public boolean search(int val) {
TreeNode cur = root;
while (cur != null) {
if (val > cur.val) {
cur = cur.right;
} else if (val < cur.val) {
cur = cur.left;
} else {
return true;
}
}
return false;
}
/**
* 插入
*/
public void insert(int val) {
//判断是否是空树
if (root == null) {
root = new TreeNode(val);
return;
}
//定义一个前驱结点
TreeNode parent = null;
//定义一个临时节点
TreeNode cur = root;
while (cur != null) {
if (val > cur.val) {
parent = cur;
cur = cur.right;
} else if (val < cur.val) {
parent = cur;
cur = cur.left;
} else {
return;
}
}
//插入的这个结点
TreeNode node = new TreeNode(val);
if (val > parent.val) {
parent.right = node;
}
if (val < parent.val) {
parent.left = node;
}
}
/**
* 删除
*/
public void remove(int key) {
TreeNode cur = root; // 当前节点初始化为根节点
TreeNode parent = null; // 记录当前节点的父节点
// 找到要删除的节点
while(cur != null) {
if(key > cur.val) {
parent = cur; // 更新父节点
cur = cur.right; // 向右子树查找
} else if(key < cur.val) {
parent = cur; // 更新父节点
cur = cur.left; // 向左子树查找
} else {
// 找到目标节点,执行删除逻辑
removeNode(parent, cur);
return; // 找到并删除后退出
}
}
System.out.println("没有该节点"); // 如果节点未找到,输出提示信息
}
// 执行删除操作的方法
private void removeNode(TreeNode parent, TreeNode cur) {
// 情况1:要删除的节点没有左子节点
if(cur.left == null) {
if(cur == root) {
root = cur.right; // 如果要删除的节点是根节点,更新根节点
} else if(cur == parent.left) {
parent.left = cur.right; // 更新父节点的左子指针
} else {
parent.right = cur.right; // 更新父节点的右子指针
}
}
// 情况2:要删除的节点没有右子节点
else if(cur.right == null) {
if(cur == root) {
root = cur.left; // 如果要删除的节点是根节点,更新根节点
} else if(cur == parent.left) {
parent.left = cur.left; // 更新父节点的左子指针
} else {
parent.right = cur.left; // 更新父节点的右子指针
}
}
// 情况3:要删除的节点有两个子节点
else {
// 找到要删除节点的右子树中的最小节点
TreeNode target = cur.right;
TreeNode targetParent = cur;
// 寻找右子树中最小节点
while(target.left != null) {
targetParent = target; // 更新最小节点的父节点
target = target.left; // 持续向左查找
}
// 用找到的最小节点的值替代要删除的节点的值
cur.val = target.val;
// 删除最小节点
if(target == targetParent.right) {
targetParent.right = target.right; // 更新父节点的右子指针
} else {
targetParent.left = target.right; // 更新父节点的左子指针
}
}
}
3.1 平衡二叉树:当且仅当任何节点的两棵子树的高度差不大于 1 的二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树,根据科学家的英文名也称为 AVL 树。
平衡二叉树本质上也是一颗二叉查找树,不过为了限制左右子树的高度差,避免出现倾斜树等偏向于线性结构演化的情况,所以对二叉搜索树中每个节点的左右子树作了限制,左右子树的高度差称之为平衡因子,树中每个节点的平衡因子绝对值不大于 1。
平衡二叉树的难点在于,当删除或者增加节点的情况下,如何通过左旋或者右旋的方式来保持左右平衡。
3.2 红黑树是一种自平衡的二叉查找树,是计算机科学中用到的一种数据结构。红黑树的每一个节点上都有存储位表示节点的颜色,可以是红或者黑;
红黑树不是高度平衡的,它的平衡是通过"红黑树的特性"进行实现的;
红黑树的特性:
1)每一个节点或是红色的,或者是黑色的。
2)根节点必须是黑色
3)每个叶节点(Nil)是黑色的;(如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点)
4)如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
5)对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点;
如下图所示就是一个
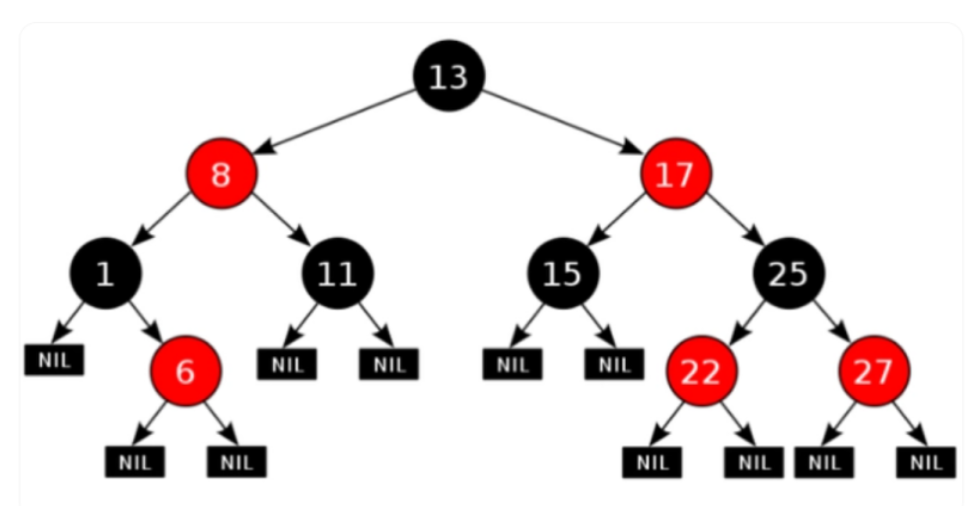
在进行元素插入的时候,和之前一样; 每一次插入完毕以后,使用黑色规则进行校验,如果不满足红黑规则,就需要通过变色,左旋和右旋来调整树,使其满足红黑规则;
- B树是一种自平衡的树数据结构,能够保持数据有序,使得查找数据、顺序访问、插入数据及删除的动作都在对数时间内完成。B树和B+树可以解决磁盘IO问题。每个磁盘页对应树的节点,平衡二叉树由于树的深度过大而造成磁盘IO读写过于频繁,导致效率不佳。为了减少磁盘IO的次数,必须降低树的深度。
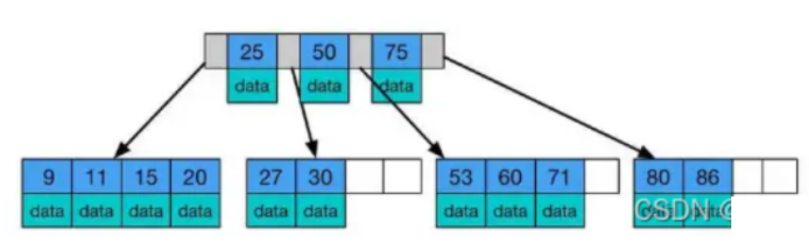
- B+ 树:B 树的变体,相对于B树来说,n叉的B+树每个节点可以存储n个key,相对于B树来说更矮更胖。
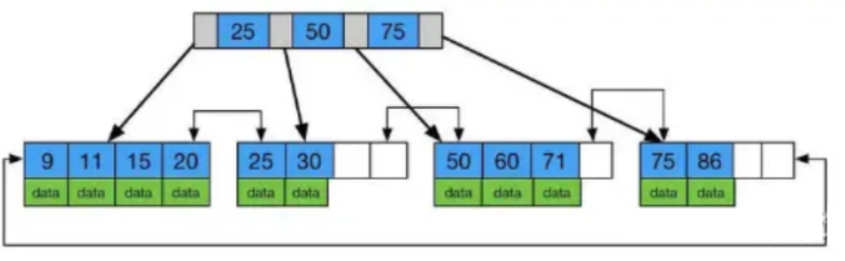
HashMap、TreeMap里面的 TreeNode 就用到了红黑树,而 B 树、B+ 树在数据库的索引原理里面有典型的应用。
(6)哈希表
哈希表(Hash Table),也称作散列表,是一种基于哈希算法实现的数据结构,可以通过关键码值(key)直接访问数据,其最大的特点是能够实现快速的查找、插入和删除操作。哈希表的主要原理是将关键码值(key)通过哈希函数映射到一个固定长度的数组(哈希表)索引(桶)上,从而实现对数据的快速定位。
哈希算法是哈希表的核心,它将任意长度的输入映射为固定长度的输出,即哈希值。常见的哈希算法包括MD5(Message Digest Algorithm 5)、SHA1(Secure Hash Algorithm 1)等。每一个 Java 对象都会有一个哈希值,默认情况就是通过调用本地方法执行哈希算法,计算出对象的内存地址 + 对象的值的关键码值。(哈希算法对于相同的值进行哈希运算得到的哈希值是相同的)
数组的最大特点就是查找容易,插入和删除困难;而链表正好相反,查找困难,而插入和删除容易。哈希表很完美地结合了两者的优点, Java8 的 HashMap 在此基础上还加入了树的优点。
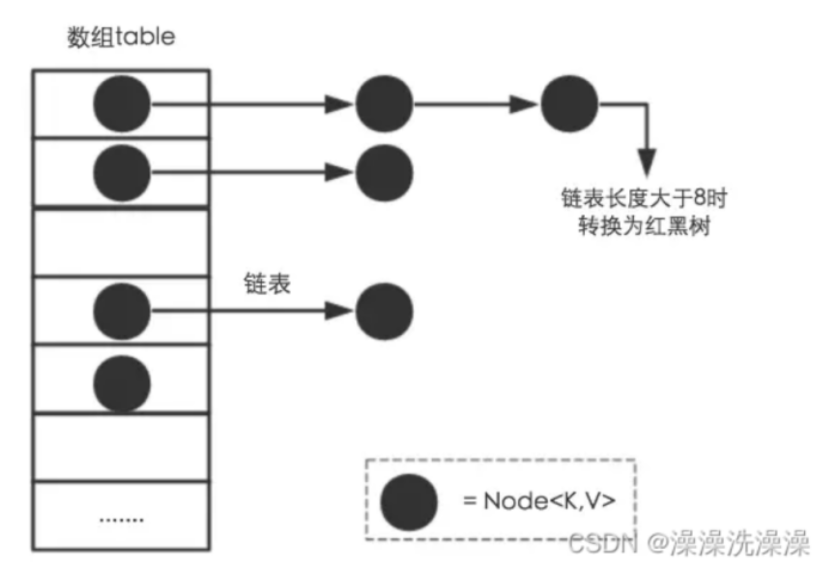
哈希表具有较快(常量级)的查询速度,以及相对较快的增删速度,所以很适合在海量数据的环境中使用。
尽管任意两个不同的数据块其哈希值相同的可能性极小,但在实际应用中仍可能发生哈希冲突(哈希碰撞)。当发生哈希冲突时,Java 的 HashMap 会采取拉链法(数组+链表)来处理冲突:即在数组的同一个位置上(桶)存储一个链表,将冲突的元素依次连接在该链表上。若链表长度超过一定阈值(通常为8),容量超过64,HashMap 会将该链表转化成红黑树,以提高查询效率。这种处理冲突的机制使得 HashMap 在面对哈希冲突时仍能保持较好的性能表现。
(7) 图
图是一种复杂的非线性结构,由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
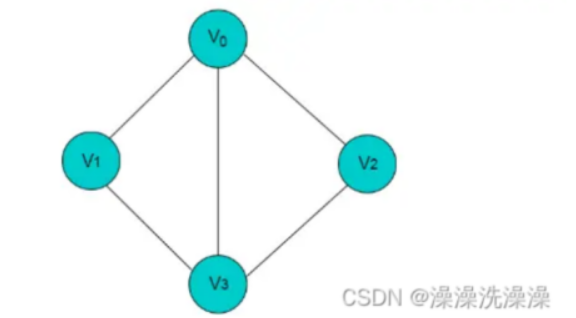
上图共有 V0,V1,V2,V3 这 4 个顶点,4 个顶点之间共有 5 条边。
在线性结构中,数据元素之间满足唯一的线性关系,每个数据元素(除第一个和最后一个外)均有唯一的"前驱"和"后继"
在树形结构中,数据元素之间有着明显的层次关系,并且每个数据元素只与上一层中的一个元素(父节点)及下一层的多个元素(子节点)相关
而在图形结构中,节点之间的关系是任意的,图中任意两个数据元素之间都有可能相关(图的相关代码同学们下去自学)。
(8) 堆
在 Java 中,堆(Heap)通常指的是二叉堆(Binary Heap),它是一种特殊的树形数据结构,常被用于实现优先队列。
二叉堆具有以下特点:
它是一个完全二叉树,即除了最底层,其他每一层都是满的,而且最底层的节点都集中在左边。
它分为大顶堆和小顶堆。在大顶堆中,父节点的值大于等于其子节点的值;在小顶堆中,父节点的值小于等于其子节点的值。
二叉堆的每个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
Java 中的 PriorityQueue 类就是基于堆实现的优先队列。堆的特性使得优先队列能够快速地进行插入和删除操作,并且能够方便地获取优先级最高(或最低)的元素。
除了二叉堆外,堆还有其他形式,如斐波那契堆等,用于解决不同类型的问题,但在 Java 中常见的是二叉堆。
堆的应用:堆排序:
(1)大顶堆&&小顶堆(图解):
1)大顶堆:
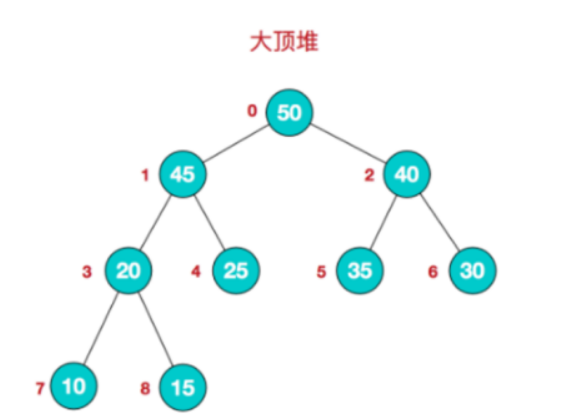
其中,二叉树节点外面标注的是堆对应的数组下标,也就是:
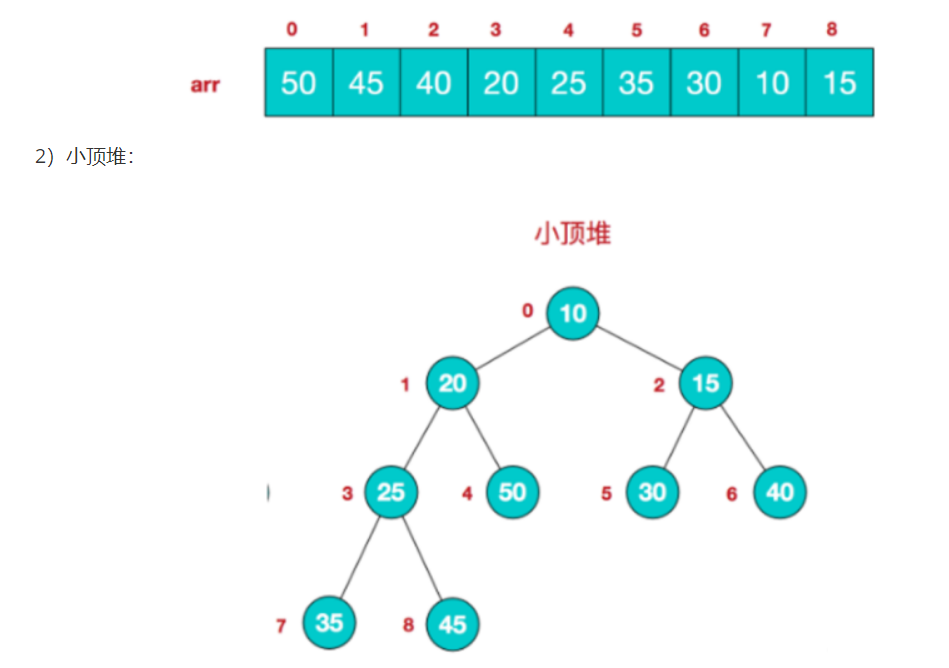
假设我们有了一个待排序的数组,并且构建好了他的逻辑结构,怎么能通过孩子找到双亲,或者通过双亲找到左右孩子呢?其实也很好理解,我们拿一颗二叉树出来就能很轻易的得出公式:
parent = (child - 1) / 2 ;
leftchild = parent * 2 + 1 ;
rightchild = parent * 2 + 2 ;
rightchild = leftchild + 1;
(2)堆排序的基本思路(这里以顺序排序为主):
-
将待排序序列构造成一个大顶堆
-
此时,整个序列的最大值就是堆顶的根节点
-
将其与末尾元素进行交换,此时末尾就为最大值
-
然后将剩余n-1个元素重新构造成一个大顶堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
①.构建大顶堆:将待排序的数组转换为最大堆。这个过程从最后一个非叶子节点开始,向上调整,直到根节点。这样可以保证每个父节点都大于或等于其子节点。
1).以给定的无序堆为例:
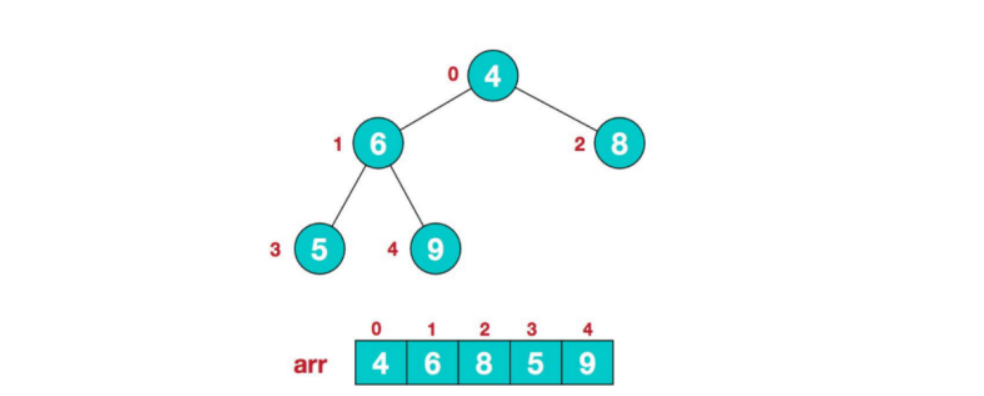
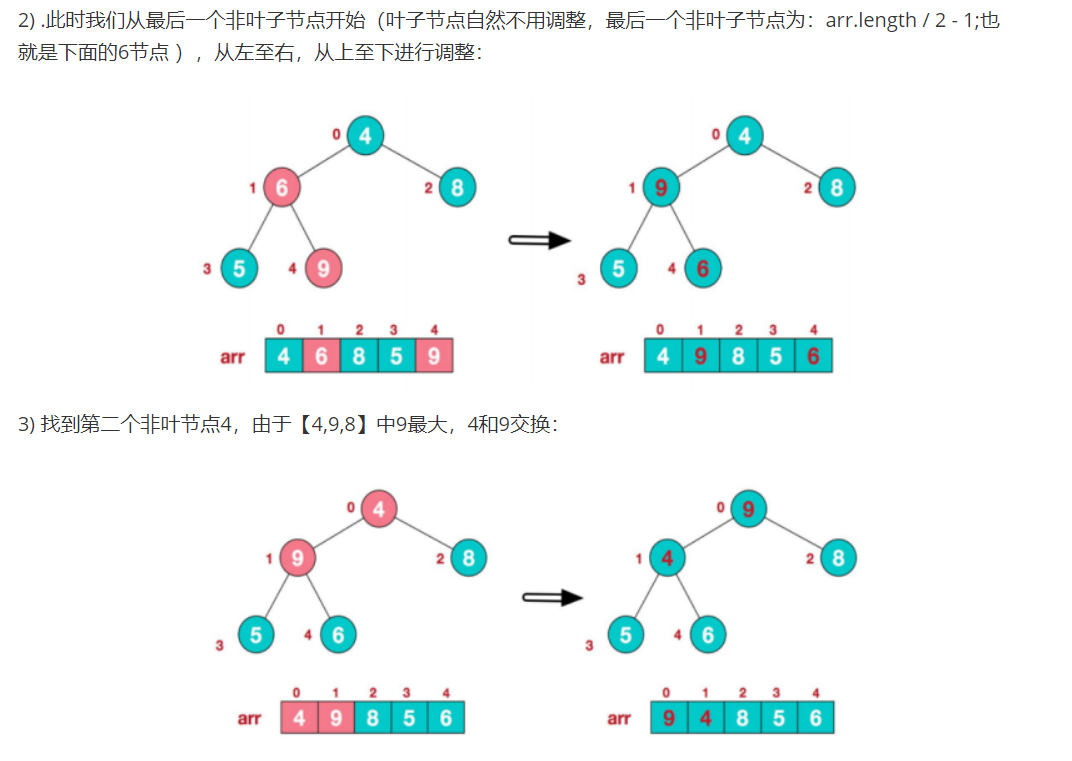
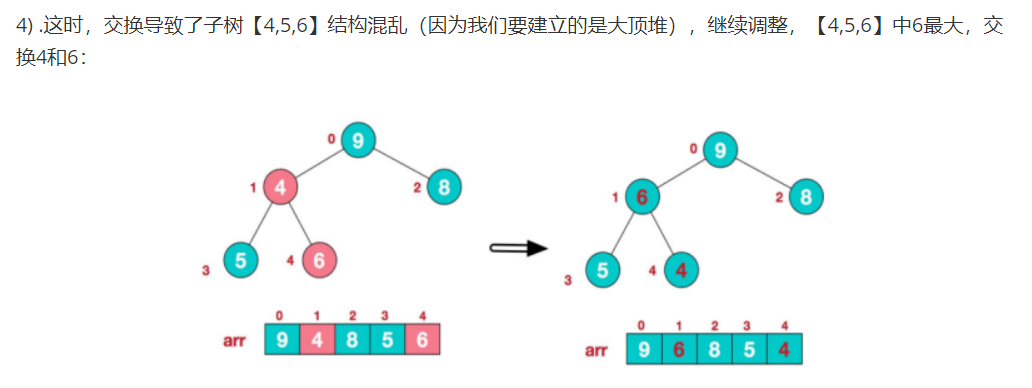
此时,我们就将一个无序序列构造成了一个大顶堆
构建大顶堆的代码:
//将一个数组(二叉树),调整为一个大顶堆
//大顶堆
/**
*
* @param arr 待调整的数组
* @param n 表示数组长度
* @param i 表示非叶子节点在数组中的索引
*/
void heapify(int arr[], int n, int i) {
int largest = i; //暂时定在i的位置就是最大值
int left = 2*i + 1;//左子结点
int right = 2*i + 2;//右子节点
//如果左子节点的值,比当前最大的值大,就把最大值的位置换成左子节点的位置
if(left < n && arr[left] > arr[largest]) {
largest = left;
}
//如果右子节点的值,比当前最大的值大,就把最大值的位置换成右子节点的位置
if(right < n && arr[right] > arr[largest]) {
largest = right;
}
//如果不相等,说明这个子节点的值有比自己大的
if(largest != i) {
swap(arr,i,largest);//就要交换位置元素
//交换位置后还需要判断子节点是否打破了最大堆的性质,是的话还需要递归调整子堆,要确保largest为根节点的堆是大顶堆
heapify(arr, n, largest);
}
}
//交换数组中的两个元素
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
②.堆排序:将堆顶元素与末尾元素进行交换,使末尾元素最大,然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素,如此反复,重建,交换:
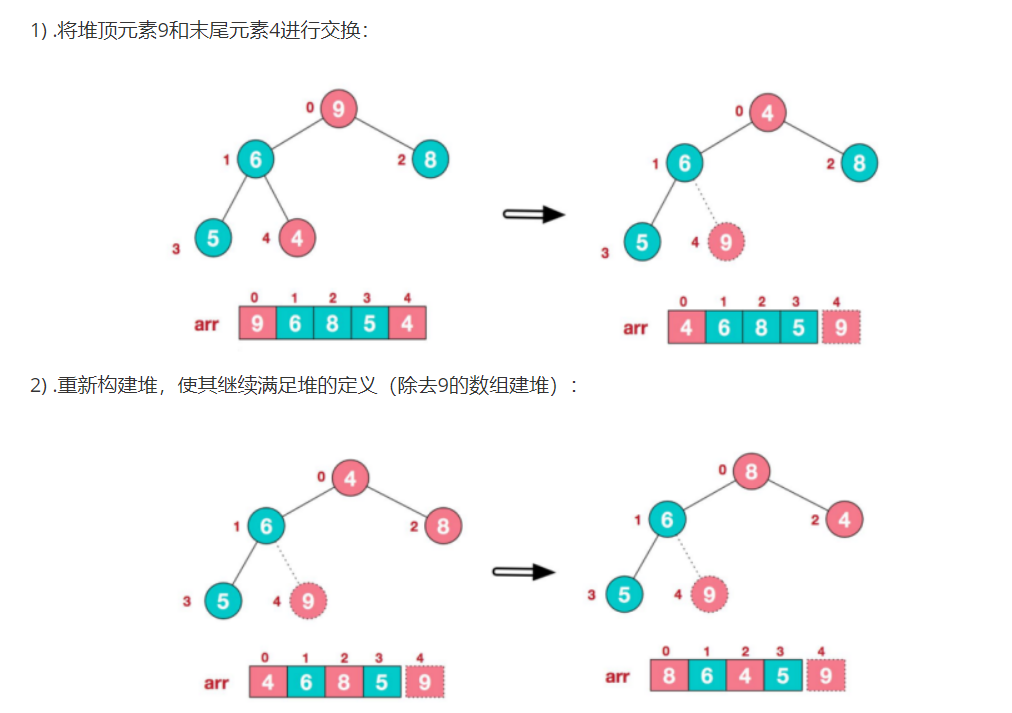
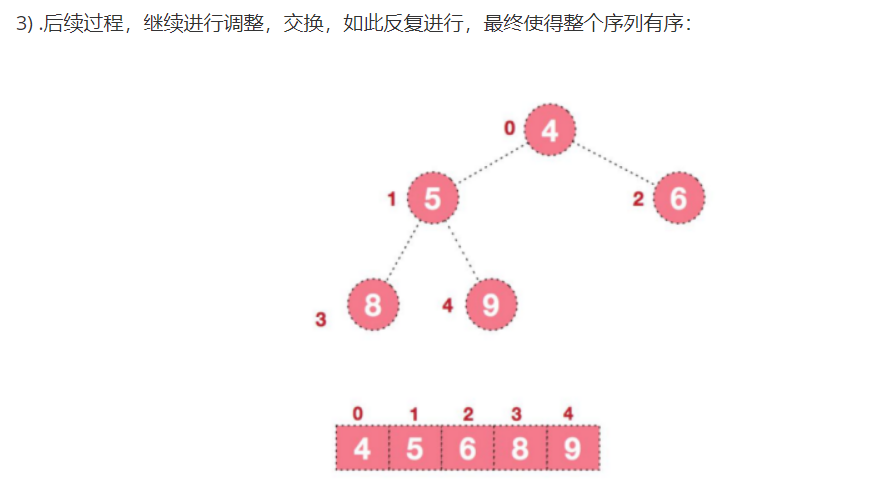
堆排序方法:
package com.edu.heap;
public class HeapSortDemo {
public static void main(String[] args) {
// TODO Auto-generated method stub
HeapSortDemo hs = new HeapSortDemo();
int [] arr = {12,11,13,5,6,7};
hs.sort(arr);
for (int i : arr) {
System.out.print(i + " ");
}
}
//将一个数组(二叉树),调整为一个大顶堆
//大顶堆
/**
*
* @param arr 待调整的数组
* @param n 表示数组长度
* @param i 表示非叶子节点在数组中的索引
*/
void heapify(int arr[], int n, int i) {
int largest = i; //暂时定在i的位置就是最大值
int left = 2*i + 1;//左子结点
int right = 2*i + 2;//右子节点
//如果左子节点的值,比当前最大的值大,就把最大值的位置换成左子节点的位置
if(left < n && arr[left] > arr[largest]) {
largest = left;
}
//如果右子节点的值,比当前最大的值大,就把最大值的位置换成右子节点的位置
if(right < n && arr[right] > arr[largest]) {
largest = right;
}
//如果不相等,说明这个子节点的值有比自己大的
if(largest != i) {
swap(arr,i,largest);//就要交换位置元素
//交换位置后还需要判断子节点是否打破了最大堆的性质,是的话还需要递归调整子堆,要确保largest为根节点的堆是大顶堆
heapify(arr, n, largest);
}
}
//交换数组中的两个元素
void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//执行堆排序
public void sort(int arr[]) {
int n = arr.length;
//构建大顶堆
for(int i = n/2-1; i >= 0; i--) {
heapify(arr, n, i);
}
//一个一个提取元素
for(int i = n - 1; i > 0; i--) {
//经过上面的一系列操作,目前arr[0]是当前数组中最大的元素,需要跟末尾元素交换
swap(arr, 0 , i);
/**
* 交换之后,最后一个元素无需再考虑排序的问题了,将剩下的元素重新构建大顶堆,这就是为什么该方法放在
* 循环里面
*/
heapify(arr, i, 0);
}
}
}
(3)代码解析
sort 方法:首先构建大顶堆,然后通过交换根节点与最后一个元素并调整堆的方式实现排序。
heapify 方法:用于维护堆的性质,确保以 i 为根节点的子树是一个最大堆。
swap 方法:用于交换数组中两个指定索引的元素。
(4)时间复杂度分析
构建堆的时间复杂度:O(n)
调整堆的时间复杂度:O(log n),因为每次调整最多需要向下遍历一层。
总体时间复杂度:O(nlog n),因为需要进行 n 次交换和调整。
(5)总结
堆排序是一种有效的排序算法,尤其适合大规模数据的排序。它的原地排序特性使得它在空间复杂度上表现优秀(O(1)),但是它不是稳定的排序算法。