leetcode 11. 盛最多水的容器 -java

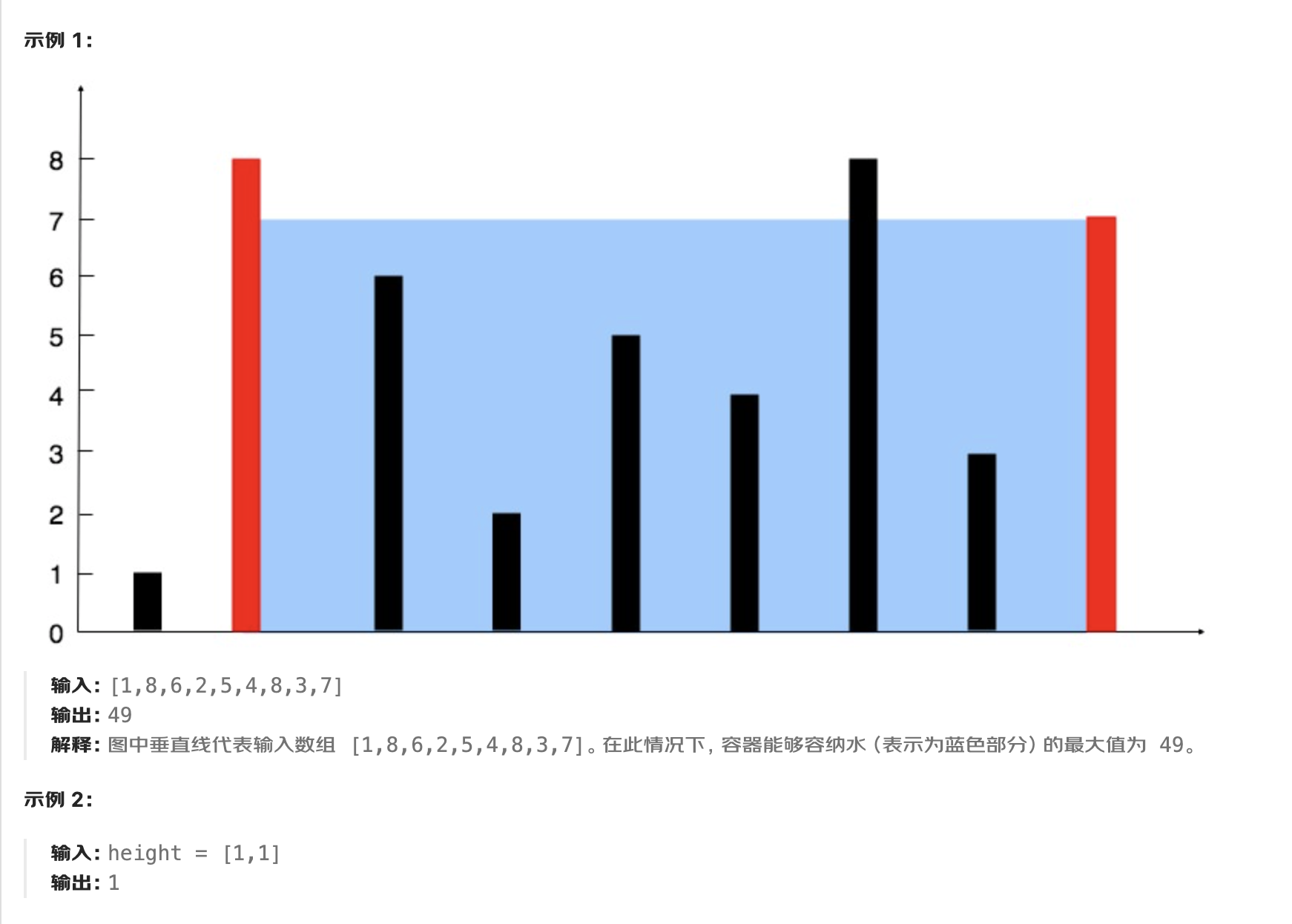
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

代码：

复制代码

public static void main(String[] args) {
    int[] height = new int[]{1,8,6,2,5,4,8,3,7};
    // 思路： 两个指针 leftIndex rightIndex  水的面积 = min(height[leftIndex],height[rightIndex]) * (rightIndex-leftIndex) 循环比较获取较大的那个面积
    Integer maxSize = 0;
    for (int leftIndex = 1; leftIndex < height.length+1 ; leftIndex++) {
        for (int rightIndex = 1; rightIndex < height.length+1 ; rightIndex++) {
            maxSize = Math.max(maxSize,Math.min(height[leftIndex],height[rightIndex])*(rightIndex-leftIndex));
        }
    }
    return maxSize;

}

双层for循环嵌套-超出时间限制

改进：接水 - 接多少水取决于短版的长度，所以可以使用双指针法，每次比较，保留较大元素的指针不动，较小元素的指针平移寻找更大的指针，直到两个指针相遇

这是因为木桶底部长度在指针在两头时是最大的，指针内移x轴长度一定会减小，这时如果想要获取更大面积，需要获取两个height里较小的那个，让他增大，面积才会增大，所以较小的元素的指针向内循环，寻找更大的值，一直到左右两个指针重合，结束循环

代码：

复制代码

public static void main(String[] args) {
    int[] height = new int[]{1,8,6,2,5,4,8,3,7};

    int left = 0, right = height.length - 1;
    int ans = 0;
    while (left < right) {
        int area = Math.min(height[left], height[right]) * (right - left);
        ans = Math.max(ans, area);
        if (height[left] <= height[right]) {
            ++left;
        }
        else {
            --right;
        }
    }
    return ans;
}

思考：遇到双层for循环，需要思考能否用双指针解决性能问题