LeetCode 热题100：160.相交链表

基础解法

时间复杂度O(m+n)，空间复杂度O(m)

1. 遍历其中一个链表，存储每个节点的地址；
2. 遍历另一个链表，若节点在数组中已有该地址，则为第一个相交点。

var getIntersectionNode = function (headA, headB) {
	let arr = [];
	let Intersected = null;
	//数组存储一个链表，判断引用类型值是否在数组里
	function traverseLink(head) {
		if (head == null) {
			return;
		}
		arr.push(head);
		return traverseLink(head.next);
	}

	traverseLink(headA);

	function Check(head) {
		if (head == null || Intersected !== null) {
			return;
		}
		if (arr.includes(head)) {
			Intersected = head;
		}
		return Check(head.next);
	}

	Check(headB);
	return Intersected;
};

---

进阶解法

时间复杂度O(m+n)，空间复杂度O(1)

参照图片，链表A指针从开始到null，链表A步长 = 链表A独立节点步长 + 公共节点步长 + 空节点；

同理，链表B步长 = 链表B独立节点步长 + 公共节点步长 + 空节点。

则有： 链表A步长 + 链表B独立节点步长 == 链表B步长 +链表A独立节点步长。

根据这个思路，当A和B指针遍历到null，跳到对方的头节点，若两个节点相等，则一定交于同一个节点（最终一定交于null）。类似快慢指针的思路。

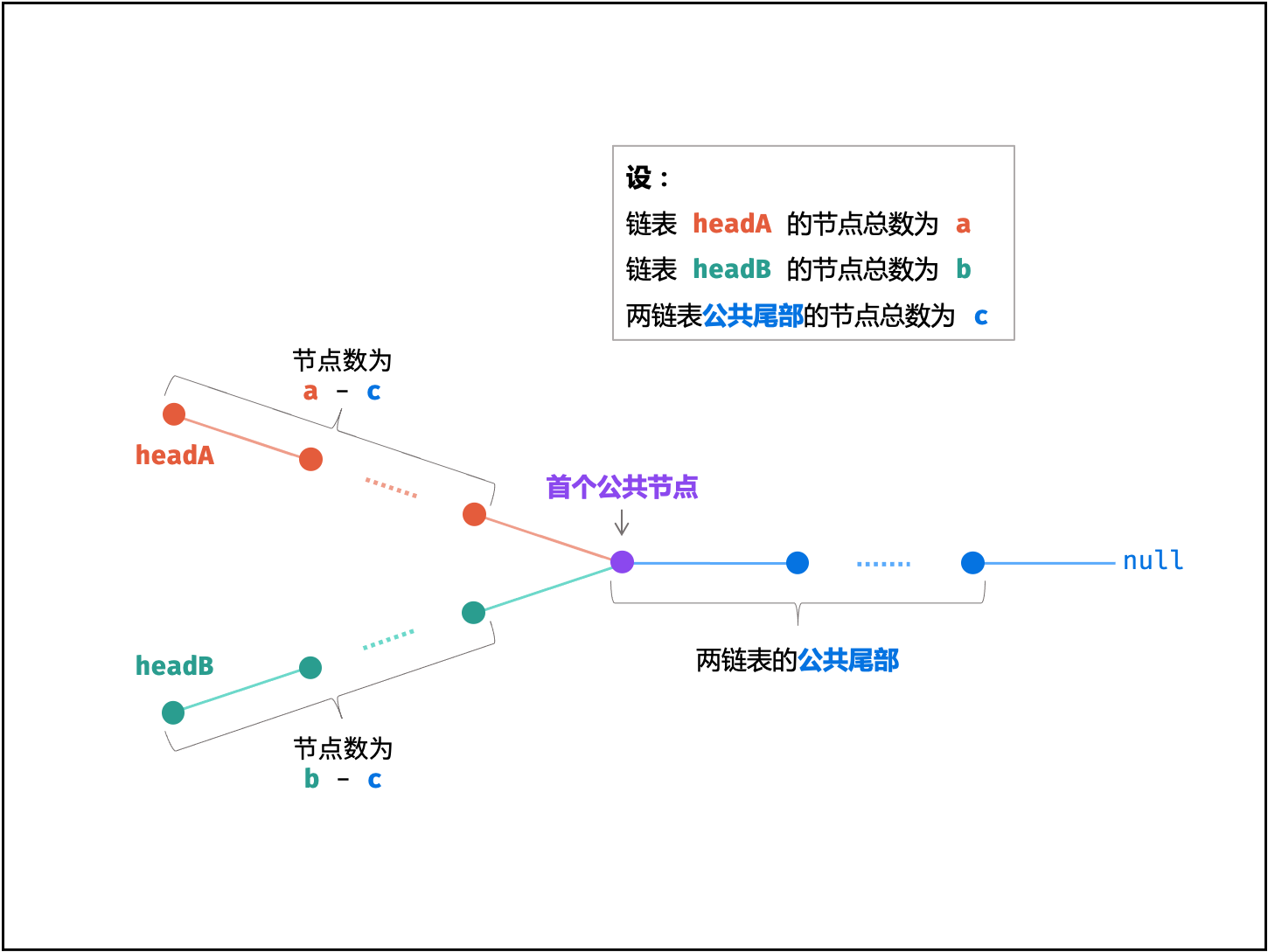代码有：

var getIntersectionNode = function (headA, headB) {
	let pointA = headA,
		PointB = headB;
	while (pointA !== PointB) {
		pointA = (pointA ? pointA.next : headB);
		PointB = (PointB? PointB.next : headA);
	}
	return pointA;
};