图机器学习（17）——基于文档语料库构建知识图谱

图机器学习（17）------基于文档语料库构建知识图谱

- [0. 前言](#0. 前言)
- [1. 基于文档语料库构建知识图谱](#1. 基于文档语料库构建知识图谱)
- [2. 知识图谱](#2. 知识图谱)
- [3. 文档-实体二分图](#3. 文档-实体二分图)

0. 前言

文本数据的爆炸性增长，直接推动了自然语言处理 (Natural Language Processing, NLP) 领域的快速发展。在本节中，通过从文档语料库中提取的信息，基于文档语料库提取的信息，介绍如何利用这些信息构建知识图谱。

1. 基于文档语料库构建知识图谱

在本节中，我们将使用自然语言处理一节中提取的信息，构建关联不同知识要素的网络图谱。我们将重点探讨两种图结构：

知识图谱 (Knowledge-based graph)：通过句子的语义推断实体间关系
二分图 (Bipartite graph)：建立文档与文本实体间的连接，后可投影为仅含文档节点或实体节点的同质图

2. 知识图谱

知识图谱的价值在于不仅能关联实体，更能赋予关系方向与语义内涵。例如比较以下两种关系：

shell 复制代码

I (->) buy (->) a book  
I (->) sell (->) a book

除 "buy/sell" 的动作差异外，关系方向性同样关键------需区分动作执行者(主语)与承受者(宾语)的非对称关系。

构建知识图谱需要实现主谓宾 (Subject-Verb-Object, SVO) 三元组提取函数，该函数将应用于语料所有句子，聚合三元组后即可生成对应图谱。
SVO 提取器可基于 spaCy 模型提供的依存句法分析实现：依存树标注既能区分主从句子结构，又可辅助识别 SVO 三元组。实际业务逻辑需处理若干特殊情况(如连词、否定结构、介词短语等)，这些均可通过规则集编码实现，且规则可根据具体用例调整优化。使用这个辅助函数，可以计算语料库中的所有三元组，并将它们存储在语料库 DataFrame 中。

python 复制代码

from subject_object_extraction import findSVOs
corpus["triplets"] = corpus["parsed"].apply(lambda x: findSVOs(x, output="obj"))

连接类型(由句子核心谓语决定)存储在 edge 列中。查看出现频率最高的 10 种关系：

python 复制代码

edges["edge"].value_counts().head(10)

最常见的边类型对应基础谓词结构。除通用动词(如 be、have、tell、give )外，我们还发现更多金融语境相关的谓词(如 buy、sell、make)。利用这些边数据，可以通过 networkx 工具函数构建知识图谱：

python 复制代码

G=nx.from_pandas_edgelist(edges, "source", "target", 
                          edge_attr=True, create_using=nx.MultiDiGraph())

通过筛选边数据表并创建子网络，可分析特定关系类型，如 "lend" 边：

python 复制代码

G=nx.from_pandas_edgelist(
    edges[edges["edge"]=="lend"], "source", "target",
    edge_attr=True, create_using=nx.MultiDiGraph()
)

下图显示了基于 "lend" 关系的子图。

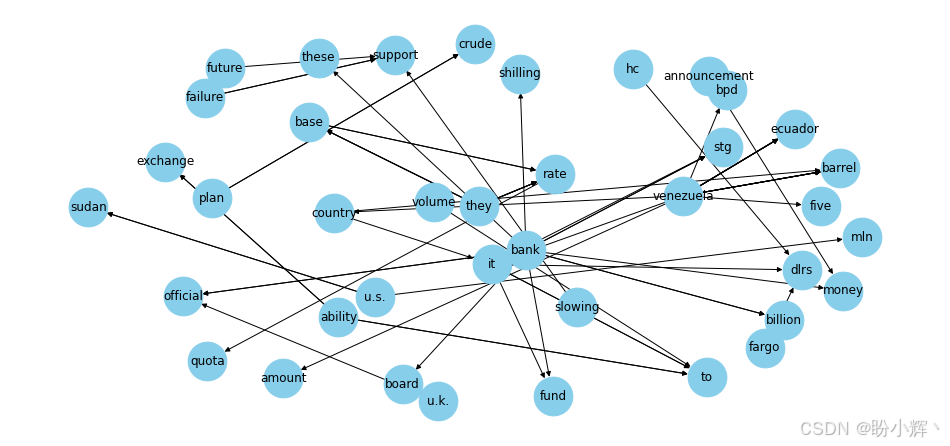
我们也可以通过筛选其他关系类型来灵活调整上述代码进行探索。接下来，我们将介绍另一种将文本信息编码为图结构的方法，该方法将运用特殊图结构------二分图。

3. 文档-实体二分图

虽然知识图谱能有效揭示实体间的聚合关系，但在某些场景下其他图表示法可能更具优势。例如当需要进行文档语义聚类时，知识图谱并非最优数据结构；同样，对于识别未共现于同一句子但频繁出现在同一文档中的间接关联(如竞品分析、相似产品发现等)，知识图谱也存在局限性。

为解决这些问题，我们将采用二分图对文档信息进行编码：为每篇文档提取最具代表性的实体，建立文档节点与对应实体节点的连接。这种结构中，单个文档节点会关联多个实体节点，而实体节点也可被多篇文档引用(形成交叉引用网络)。这种交叉引用关系可衍生出实体间、文档间的相似度度量，进而支持将二分图投影为纯文档节点或纯实体节点的同质图。

为了构建二分图，需要提取文档中的相关实体。"相关实体"在当前的上下文中，可以视为命名实体(例如，由命名实体识别引擎识别的组织、人物或地点)或关键词；即，能够识别并通常描述文档及其内容的词(或词的组合)。

关键词提取算法众多，其中基于 TF-IDF 评分的方法较为经典：该算法通过计算词元(或词元组合 n-gram )的得分进行筛选，得分与文档内词频 (Term Frequency) 成正比，与语料库中出现该词的文档频率 (Inverse Document Frequency) 成反比：
c i , j ∑ c i , j ⋅ l o g N 1 + D i \frac{c_{i,j}}{\sum c_{i,j}}\cdot log\frac N{1+D_i} ∑ci,jci,j⋅log1+DiN

其中， c i , j c_{i,j} ci,j 表示文档 j j j 中词语 i i i 的计数， N N N 表示语料库中的文档数量， D i D_i Di 表示词 i i i 出现的文档。因此，TF-IDF 评分机制会提升文档中高频出现的词汇权重，同时降低常见词汇(往往缺乏代表性)的得分。
TextRank 算法同样基于文档的图结构表示。TextRank 算法构建的网络中，节点是单个词元，边则由特定滑动窗口内共现的词元对形成。网络构建完成后，通过 PageRank 算法计算各词元的中心度得分，据此对文档内词汇进行重要性排序。最终选取中心度最高的节点(通常占文档总词量的 5%-20% )作为候选关键词。当多个候选关键词相邻出现时，它们会被合并为多词复合关键词。

(1) 利用 gensim 库可以直接使用 TextRank 算法：

python 复制代码

from gensim.summarization import keywords
text = corpus["clean_text"][0]
keywords(text, words=10, split=True, scores=True, pos_filter=('NN', 'JJ'), lemmatize=True)

输出结果如下所示：

shell 复制代码

[('trading', 0.4615130639538529),
 ('said', 0.3159855693494515),
 ('export', 0.2691553824958079),
 ('import', 0.17462010006456888),
 ('japanese electronics', 0.1360932626379031),
 ('industry', 0.1286043740379779),
 ('minister', 0.12229815662000462),
 ('japan', 0.11434500812642447),
 ('year', 0.10483992409352465)]

这里的评分代表中心度 (centrality)，反映了特定词元的重要性。可以看到，算法还可能生成复合词元。我们可以实现关键词提取功能来计算整个语料库的关键词，并将结果存储到语料 DataFrame 中：

python 复制代码

corpus["keywords"] = corpus["clean_text"].apply(
    lambda text: keywords(text, words=10, split=True, scores=True, pos_filter=('NN', 'JJ'), lemmatize=True)
)

(2) 除了关键词，构建二分图还需要解析 NER 引擎提取的命名实体，并以与关键词相似的数据格式进行编码：

python 复制代码

def extractEntities(ents, minValue=1, typeFilters=["GPE", "ORG", "PERSON"]):
    entities = pd.DataFrame([
        {"lemma": e.lemma_, "lower": e.lemma_.lower(), "type": e.label_}
        for e in ents if hasattr(e, "label_")
    ])

    if len(entities)==0:
        return pd.DataFrame()
    
    g = entities.groupby(["type", "lower"])

    summary = pd.concat({
        "alias": g.apply(lambda x: x["lemma"].unique()), 
        "count": g["lower"].count()
    }, axis=1)
    
    return summary[summary["count"]>1].loc[pd.IndexSlice[typeFilters, :, :]]

def getOrEmpty(parsed, _type):
    try:
        return list(parsed.loc[_type]["count"].sort_values(ascending=False).to_dict().items())
    except:
        return []

def toField(ents):
    typeFilters=["GPE", "ORG", "PERSON"]
    parsed = extractEntities(ents, 1, typeFilters)
return pd.Series({_type: getOrEmpty(parsed, _type) for _type in typeFilters})

(3) 解析 spacy 标签：

python 复制代码

entities = corpus["parsed"].apply(lambda x: toField(x.ents))

(4) 通过 pd.concat 函数可以将实体 DataFrame 与语料 DataFrame 合并，从而将所有信息整合到单一数据结构中：

python 复制代码

merged = pd.concat([corpus, entities], axis=1)

(5) 现在我们已经具备构建二分图的所有要素，可以通过循环遍历所有文档-实体或文档-关键词对来创建边列表：

python 复制代码

edges = pd.DataFrame([
    {"source": _id, "target": keyword, "weight": score, "type": _type}
    for _id, row in merged.iterrows()
    for _type in ["keywords", "GPE", "ORG", "PERSON"] 
    for (keyword, score) in row[_type]
])

(6) 边列表创建完成后，即可使用 networkx API 生成二分图：

python 复制代码

G = nx.Graph()
G.add_nodes_from(edges["source"].unique(), bipartite=0)
G.add_nodes_from(edges["target"].unique(), bipartite=1)
G.add_edges_from([
    (row["source"], row["target"])
    for _, row in edges.iterrows()
])

接下来，我们将把这个二分图投影到任意一组节点(实体或文档)上。使我们能够探索两种图之间的差异，并使用无监督技术对术语和文档进行聚类。然后，我们将回到二分图，通过利用网络信息进行监督分类任务。

2.2.1 实体-实体图

我们首先将图投影到实体节点集合上。NetworkX 提供了一个专门处理二分图的子模块 networkx.algorithms.bipartite，其中已实现了多种算法，networkx.algorithms.bipartite.projection 子模块提供了若干实用函数，可将二分图投影到特定节点子集上。在执行投影之前，我们需要利用创建图时设置的 "bipartite" 属性来提取特定集合(文档或实体)的节点：

python 复制代码

document_nodes = {n for n, d in G.nodes(data=True) if d["bipartite"] == 0}
entity_nodes = {n for n, d in G.nodes(data=True) if d["bipartite"] == 1}

图投影本质上会创建一个由选定节点组成的新图。节点之间边的建立取决于它们是否拥有共同邻居节点。基础的 projected_graph 函数会生成一个边未加权的网络。但通常更具信息量的做法是根据共同邻居的数量为边赋予权重，投影模块提供了基于不同权重计算方式的多种函数。在下一节中，我们将使用 overlap_weighted_projected_graph 函数，该函数基于共同邻居采用 Jaccard 相似度计算边权重。我们也可以探索其它函数，根据具体应用场景选择最适合的方案。

2.2.2 维度问题

在进行图投影时还需特别注意一个问题：投影后图的维度。在某些情况下，投影可能会产生数量庞大的边，导致图难以分析。在我们的使用场景中，按照我们用来创建网络的逻辑，一个文档节点至少连接到 10 个关键词和若干实体节点。在最终的实体-实体图中，这些实体之间都会因为至少拥有一个共同邻居(包含它们的文档)而相互连接。因此单文档就会生成约 15 × 14 2 ≈ 100 \frac {15×14}2\approx 100 215×14≈100 条边。如果我们将这个数字乘以文档的数量 ( ∼ 1 0 5 \sim 10^5 ∼105)，即便在本节的简单场景中也会产生数百万条边，几乎无法处理。虽然这显然是个保守上限(因为某些实体共现关系会出现在多个文档中而不会重复计算)，但已能反映可能面临的复杂度量级。因此建议，根据底层网络的拓扑结构和图规模，实施二分图投影前务必谨慎。

为了降低复杂度使投影可行，可以仅保留达到特定度数的实体节点。大多数复杂性来自于那些仅出现一次或少数次、却仍在图中形成团结构的实体节点。这类实体对模式捕捉和洞见发现的贡献度很低，且可能受到统计波动性的强烈干扰。相反，我们应聚焦于那些高频出现、能提供更可靠统计结果的强相关性实体。

为此，我们将仅保留度数 ≥5 的实体节点，具体方法是生成经过过滤的二分子图：

python 复制代码

nodes_with_low_degree = {n for n, d in nx.degree(G, nbunch=entity_nodes) if d<5}

对该子图进行投影，而不会生成边数过多的图：

python 复制代码

entityGraph = overlap_weighted_projected_graph(
    subGraph, 
    {n for n, d in subGraph.nodes(data=True) if d["bipartite"] == 1}
)

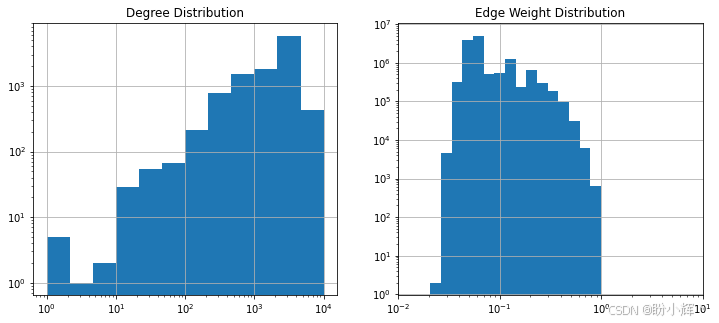
尽管我们已应用过滤条件，但图的边数和平均节点度数仍然相当大。下图展示了节点度数和边权重的分布情况，可以观察到，度数分布在较低值处出现一个峰值，但向高值方向呈现长尾分布；边权重也表现出类似趋势，峰值出现在较低值区间，但右侧同样具有长尾特征。这些分布特征表明图中存在多个小型社区(即团结构)，它们通过某些中心节点相互连接。

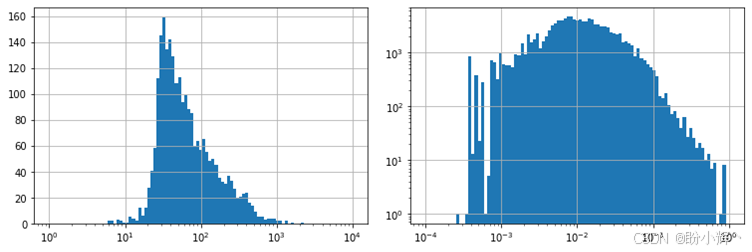
边权重的分布情况也表明可以应用第二个过滤器。在二分图上实施的实体度数过滤，帮助我们筛除了仅出现在少数文档中的低频实体。但由此得到的图结构可能会面临相反的问题：高频实体之间可能仅仅因为共同出现在多个文档中就产生连接，即便它们之间并不存在有意义的因果关系。以江苏和苏州为例，这两个实体几乎必然存在连接，因为极有可能存在至少一个或多个文档同时提及它们。但若二者之间缺乏强因果关联，它们的Jaccard相似度就不太可能达到较高值。仅保留权重最高的边，能让我们聚焦于最相关且可能稳定的关系。边权重分布表明，将阈值设定为 0.05 较为合适：

python 复制代码

filteredEntityGraph = entityGraph.edge_subgraph(
    [edge for edge in entityGraph.edges if entityGraph.edges[edge]["weight"]>0.05]
)

该阈值能显著减少边的数量，使网络分析具备可操作性。

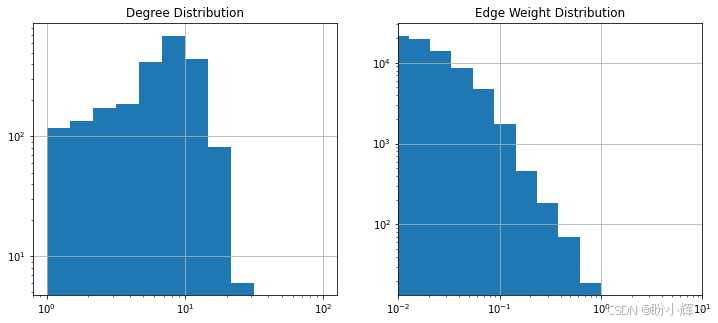
上图展示了过滤后图的节点度数与边权重的分布情况，可以看到当前分布显示节点度数在 10 左右出现峰值。

2.2.3 图分析

通过 Gephi 生成的网络全景如下所示：

(1) 为深入理解网络拓扑特性，我们计算了平均最短路径长度、聚类系数和全局效率等宏观指标。虽然该图包含五个连通分量，但最大分量几乎涵盖整个网络------在 2265 个节点中占据了 2254 个：

python 复制代码

components = nx.connected_components(filteredEntityGraph)
pd.Series([len(c) for c in components])

(2) 获取最大连通分量的全局属性：

python 复制代码

comp = components[0]
global_metrics = pd.Series({
    "shortest_path": nx.average_shortest_path_length(comp),
    "clustering_coefficient": nx.average_clustering(comp),
    "global_efficiency": nx.global_efficiency(comp)
})

输出结果如下所示：

shell 复制代码

{
    'shortest_path': 4.715073779178782,
    'clustering_coefficient': 0.21156314975836915,
    'global_efficiency': 0.22735551077454275
}

从这些指标的数值(最短路径约 5，聚类系数约 0.2) 结合度数分布可以看出，该网络由多个规模有限的社区组成。局部属性(如度数、PageRank 和中介中心性分布)如下图所示，这些指标之间往往存在相互关联性：

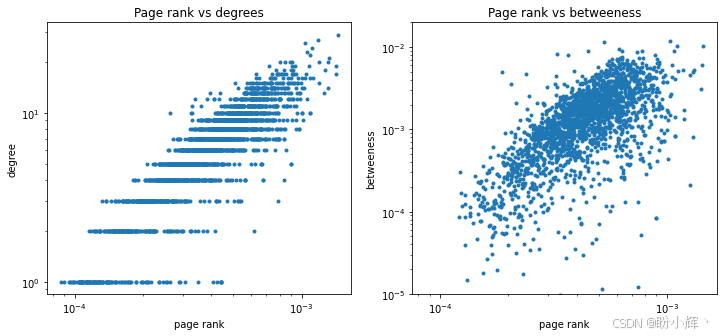
在完成网络局部/全局指标的描述及整体可视化后，我们将应用无监督学习技术来挖掘网络中的深层信息。

(3) 首先使用 Louvain 社区检测算法，该算法通过模块度优化，旨在将节点划分至互不重叠的最佳社区结构中：

python 复制代码

import community
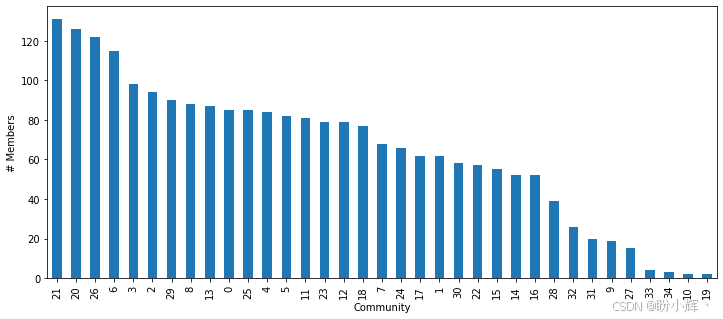
communities = community.best_partition(filteredEntityGraph)

大约可以得到 30 个社区，其成员数量分布与下图所示，其中较大规模的社区一般包含 130-150 篇文档。

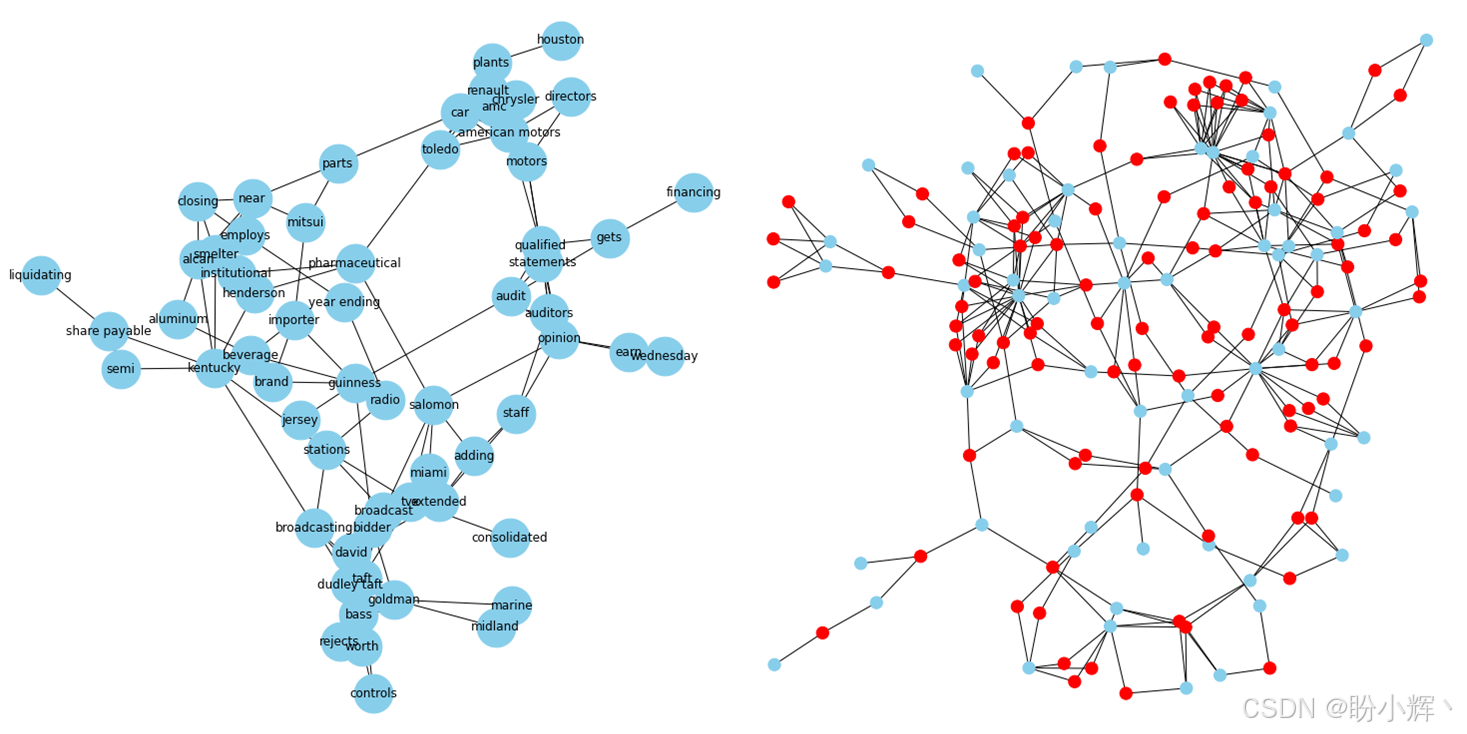
下图展示了其中一个社区的细节视图，从中可识别特定主题。左侧除实体节点外，还可看到文档节点，由此揭示了关联二分图的结构：

(4) 通过节点嵌入技术可以提取关于实体间拓扑关系与相似性的深层信息。我们可以采用 Node2Vec 方法------该方法通过将随机生成的游走序列输入 skip-gram 模型，将节点映射至向量空间，使拓扑相近的节点在嵌入空间中位置邻近：

python 复制代码

from node2vec import Node2Vec
node2vec = Node2Vec(filteredEntityGraph, dimensions=5)
model = node2vec.fit(window=10)
embeddings = model.wv

在嵌入向量空间中，我们可以应用传统聚类算法(如高斯混合模型、K-Means 或 DBSCAN)。我们还能通过 t-SNE 将嵌入向量投影至二维平面，实现聚类与社区的可视化。Node2Vec 不仅为图中社区识别提供了另一种解决方案，还能像经典 Word2Vec 那样计算词语相似度。例如，我们可以查询 Node2Vec 嵌入模型，找出与 "turkey" 最相似的词语，从而获取语义关联词：

python 复制代码

[('turkish', 0.9975333213806152),
('lira', 0.9903393983840942),
('rubber', 0.9884852170944214),
('statoil', 0.9871745109558105),
('greek', 0.9846569299697876),
('xuto', 0.9830175042152405),
('stanley', 0.9809650182723999),
('conference', 0.9799597263336182),
('released', 0.9793018102645874),
('inra', 0.9775203466415405)]

尽管 Node2Vec 与 Word2Vec 在方法上存在相似性，但两种嵌入方案的信息来源截然不同：Word2Vec 直接基于文本构建，捕捉句子层面的词语关系；而 Node2Vec 源自实体-文档二分图，其编码的特征更倾向于文档层面的描述。

2.2.4 文档-文档图

接下来，我们将二分图投影至文档节点集，构建可分析的文档关联网络。与创建实体关联网络类似，这里采用 overlap_weighted_projected_graph 函数生成带权图，并通过过滤保留显著性边。需要注意的是，网络的拓扑结构以及构建二分图时使用的业务逻辑并不鼓励形成团(即完全图)，正如在实体-实体图中看到的那样：只有当两个节点至少共享一个关键词、组织、地点或人时，它们才会连接。在 10-15 个节点组成的群组中(如实体节点群组)，这种情况虽可能发生，但概率较低。

(1) 接下来，快速构建网络：

python 复制代码

documentGraph = overlap_weighted_projected_graph(
    G,
    document_nodes
)

下图展示了节点度数与边权重的分布情况，这有助于我们确定过滤边时所采用的阈值。值得注意的是，与实体-实体图的度数分布相比，当前节点度数分布明显向高值区域偏移，表明存在多个具有超高连接度的"超级节点"。同时，边权重分布显示杰卡德指数倾向于接近1的数值，远高于实体-实体图中的观测值。这两项发现揭示了两个网络的本质差异：实体-实体图以大量紧密连接的社区(即完全子图)为特征，而文档-文档图则呈现"核心-边缘"结构------高度连接的大度数节点构成网络核心，外围则分布着弱连接或孤立节点：

(2) 将所有边存储至 DataFrame 中，这样既能实现可视化呈现，又可基于该数据集进行过滤以生成子图：

python 复制代码

allEdgesWeights = pd.Series({
    (d[0], d[1]): d[2]["weight"]
    for d in documentGraph.edges(data=True)
})

观察上图可知，将边权重阈值设定为 0.6 较为合理，这样可通过 networkx 的 edge_subgraph 函数生成更易处理的网络：

python 复制代码

filteredDocumentGraph = documentGraph.edge_subgraph(
    allEdgesWeights[(allEdgesWeights>0.6)].index.tolist()
)

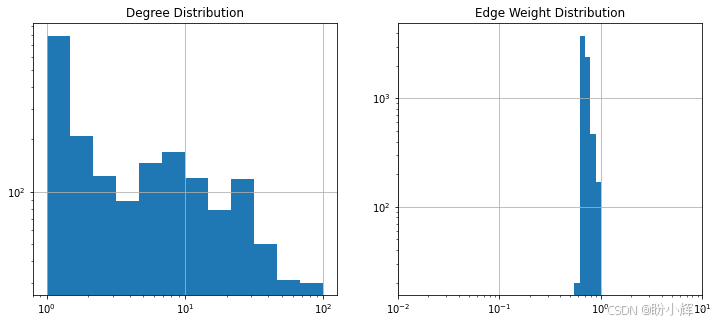
下图展示了精简后的网络在节点度数与边权重上的分布情况：

文档-文档图与实体-实体图在拓扑结构上的本质差异，在下文完整的网络可视化图中更为明显。文档-文档网络呈现"核心-卫星"结构------由紧密连接的核心网络与多个弱连接的卫星节点构成。这些卫星节点代表那些未共享或仅共享少量关键词/实体的文档，其中完全孤立的文档数量相当庞大，约占总量的 50%：

(3) 提取该网络的连通分量：

python 复制代码

components = pd.Series({
    ith: component
    for ith, component in enumerate(
        nx.connected_components(filteredDocumentGraph)
    )
})

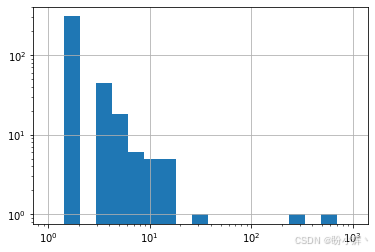
下图展示了连通分量的规模分布情况。可以清晰观察到若干超大聚类(核心集群)与大量孤立或极小分量(边缘卫星集群)并存的现象。这种结构与我们在实体-实体图中观察到的结构截然不同，在实体-实体图中，所有节点归属于单一超大连通集群：

(4) 从完整图中提取由最大连通分量构成的子图：

python 复制代码

coreDocumentGraph = nx.subgraph(
    filteredDocumentGraph,
    [node
    for nodes in components[components.apply(len)>8].values
    for node in nodes]
)

观察核心网络的 Gephi 可视化结果(下图右侧)，可以发现，该核心网络由若干社区组成，其中包含多个彼此紧密连接的高度数节点。

与处理实体-实体网络时类似，我们可以处理网络以识别嵌入在图中的社区。然而，不同之处在于，文档-文档图现在提供了一个使用文档标签来判断聚类的手段。实际上，属于同一主题的文档应当彼此邻近且相互连接。此外，这种方法还能帮助我们识别不同主题之间的相似性。

(5) 首先，提取候选社区：

python 复制代码

import community
communities = pd.Series(
    community.best_partition(filteredDocumentGraph)
)

(6) 随后分析各社区内的主题分布，检测是否存在同质性(所有文档属于同一类别)或主题间的相关性：

python 复制代码

from collections import Counter
def getTopicRatio(df):
    return Counter([label
                    for labels in df["label"]
                    for label in labels])
communityTopics = pd.DataFrame.from_dict({
    cid: getTopicRatio(corpus.loc[comm.index])
    for cid, comm in communities.groupby(communities)
}, orient="index")
normalizedCommunityTopics = (
    communityTopics.T / communityTopics.sum(axis=1)
).T

normalizedCommunityTopics 是一个 DataFrame 结构，其中每一行代表一个社区 (community)，每一列对应不同主题的分布比例(以百分比形式呈现)。为了量化这些社区/集群内部主题混合的异质性，我们需要计算每个社区的香农熵 (Shannon entropy)：
I c = − ∑ i l o g t c i Ic=−∑ilogt{ci} Ic=−i∑logtci

其中， I c Ic Ic 表示社区 c c c 的熵值，$t_{ci} 表示社区 c c c 中主题 i i i 的占比。接下来，我们需要为所有社区计算经验香农熵：

python 复制代码

normalizedCommunityTopics.apply(
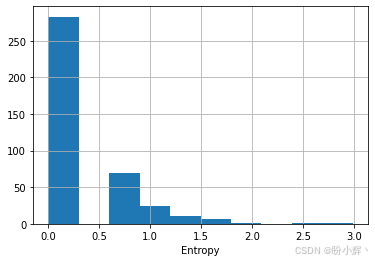
    lambda x: np.sum(-np.log(x)), axis=1)

下图展示了所有社区的熵值分布情况。大多数社区的熵值为零或接近零，这表明相同类别(标签)的文档倾向于聚集在一起：

尽管大多数社区在主题分布上呈现零变异或低变异，但当某些社区表现出异质性时，探究主题间的关联仍具有意义。为此，我们计算主题分布之间的相关性

python 复制代码

topicsCorrelation = normalizedCommunityTopics.corr().fillna(0)

然后，使用主题-主题网络表示和可视化这些相关性：

python 复制代码

topicsCorrelation[topicsCorrelation<0.8] = 0
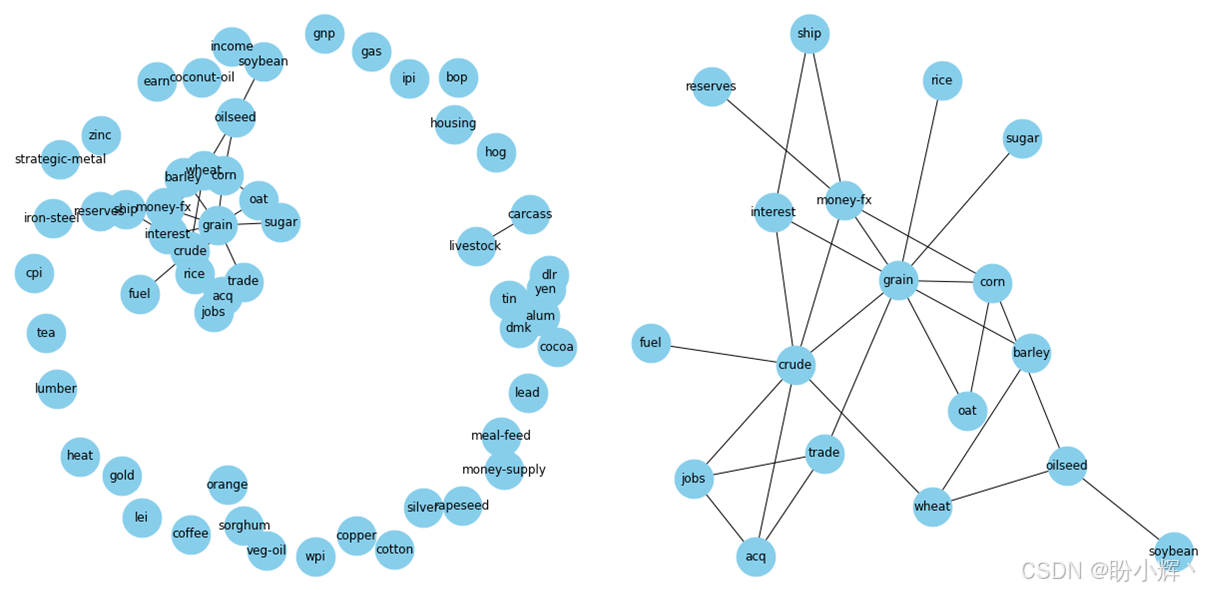
topicsGraph = nx.from_pandas_adjacency(topicsCorrelation)

下图左侧展示了主题网络的完整图表示。与文档-文档网络类似，主题网络呈现出"核心-边缘"结构------边缘由孤立节点构成，核心则是高度连通的节点集群。右图聚焦展示了核心网络的细节，其中商品类主题之间的强相关性反映出明确的语义关联：

本节我们分析了文档及文本源分析中产生的各类网络结构，通过全局与局部属性统计描述网络特征，并运用无监督算法揭示了图中的潜在结构。