OpenCV-图像预处理➁【图像插值方法、边缘填充策略、图像矫正、掩膜应用、水印添加，图像的噪点消除】

欧阳小猜2025-07-27 12:49

文章目录

先言

在计算机视觉的实际应用中，优质的图像预处理往往能决定算法的成败。继上篇介绍的基础预处理技术后，本文将深入探讨更高级的OpenCV图像处理技巧，帮助您解决实际项目中常见的棘手问题。

从精细的图像插值方法选择，到实用的边缘填充策略；从专业的图像矫正技术，到灵活的掩膜应用；再到商业场景中必不可少的水印添加，以及提升图像质量的噪点消除方法------本文将系统性地介绍这些进阶预处理技术，并辅以可落地的代码实现，带您掌握OpenCV更强大的图像处理能力。

一、图像插值方法深度解析

在图像处理和计算机图形学中，插值（Interpolation）是一种通过已知数据点之间的推断或估计来获取新数据点的方法。它在图像处理中常用于处理图像的放大、缩小、旋转、变形等操作，以及处理图像中的像素值。

图像插值算法是为了解决图像缩放或者旋转等操作时，由于像素之间的间隔不一致而导致的信息丢失和图像质量下降的问题。当我们对图像进行缩放或旋转等操作时，需要在新的像素位置上计算出对应的像素值，而插值算法的作用就是根据已知的像素值来推测未知位置的像素值。

1.最近邻插值（CV.INTER_NEAREST）

复制代码 
new_img1=cv.warpAffine(img,M,(w,h),flags=cv.INTER_NEAREST)

首先给出目标点与原图像点之间坐标的计算公式：
s r c X = d s t X ∗ s r c W i d t h d s t W i d t h s r c X=d s t X*{\frac{s r c Width}{d s t Width}} srcX=dstX∗dstWidthsrcWidth
s r c Y = d s t Y ∗ s r c H e i g h t d s t H e i g h t s r cY=d s t Y*{\frac{s r c H e i g h t}{d s t H e i g h t}} srcY=dstY∗dstHeightsrcHeight

​

dstX：目标图像中某点的x坐标，

dstY：目标图像中某点的y坐标，

srcWidth：原图的宽度，

dstWidth：目标图像的宽度；

srcHeight：原图的高度，

dstHeight：目标图像的高度。

  • 而srcX和srcY：目标图像中的某点对应的原图中的点的x和y的坐标。

通俗的讲，该公式就是让目标图像中的每个像素值都能找到对应的原图中的像素值，这样才能根据不同的插值方法来获取新的像素值。根据该公式，我们就可以得到每一个目标点所对应的原图像的点.

代码如下（示例）：

python 复制代码 
import cv2 as cv
#读图
cat = cv.imread("../images/1.jpg")
#获取旋转矩阵
M = cv.getRotationMatrix2D((cat.shape[1]//2,cat.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]))
cv.imshow("dst",dst)
#最近邻插值
dst1 = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]),cv.INTER_NEAREST)
cv.imshow("dst1",dst1)
cv.waitKey(0)
cv.destroyAllWindows()

插值法的主要目的是为了将转换后在原图中对应的像素坐标出现非整数的的情况，为了能够精准找到原图像素坐标，不同的插值方法对原图的像素点坐标确认方式不同罢了，下面的插值方式都是这个目的。

2.双线性插值（CV2.INTER_LINEAR）

双线性插值是一种图像缩放、旋转或平移时进行像素值估计的插值方法。当需要对图像进行变换时，特别是尺寸变化时，原始图像的某些像素坐标可能不再是新图像中的整数位置，这时就需要使用插值算法来确定这些非整数坐标的像素值。

双线性插值的工作原理是这样的：

  1. 假设要查找目标图像上坐标为 (x', y') 的像素值，在原图像上对应的浮点坐标为 (x, y)。
  2. 在原图像上找到四个最接近(x, y)的像素点，通常记作 P00(x0, y0), P01(x0, y1), P10(x1, y0), P11(x1, y1)，它们构成一个2x2的邻域矩阵。
  3. 分别在水平方向和垂直方向上做线性插值：
  • 水平方向：根据 x 与 x0 和 x1 的关系计算出 P00 和 P10 、 P01和 P11 之间的插值结果。
  • 垂直方向：将第一步的结果与 y 与 y0 和 y1 的关系结合，再在垂直方向上做一次线性插值。
  1. 综合上述两次线性插值的结果，得到最终位于 (x', y') 处的新像素的估计值。

我们还是得了解一下线性插值法：

原理 ：线性插值是一种在已知两点之间估算中间值的方法，假设变化是线性的。

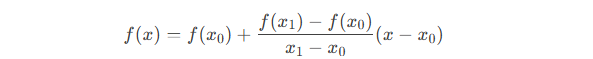
在图像缩放时，需要对像素进行二维插值。双线性插值通过三次一维线性插值实现：

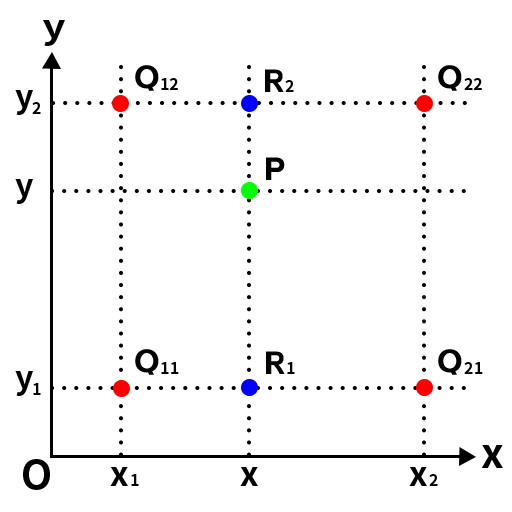
以上图为例先计算Q12-Q22的中间值得到R2，在计算Q11与Q21的中间值R1，之后在计算R1与R2 的中间值得到最终的像素值
数学本质： 加权平均计算，距离越近的原始像素权重越大

示例代码：

python 复制代码 
import cv2 as cv
#读图
cat = cv.imread("../images/1.jpg")
#获取旋转矩阵
M = cv.getRotationMatrix2D((cat.shape[1]//2,cat.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]))
cv.imshow("dst",dst)
#双线性插值 单线性插值，插两次，水平垂直
dst2 = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]),cv.INTER_LINEAR)
cv.imshow("dat2",dst2)
cv.waitKey(0)
cv.destroyAllWindows()

3.像素区域插值（cv2.INTER_AREA）

像素区域插值主要分两种情况，缩小图像和放大图像的工作原理并不相同。

  • 当使用像素区域插值方法进行缩小图像时，它就会变成一个均值滤波器（同往期章节自适应二值化中的均值卷积核），其工作原理可以理解为对一个区域内的像素值取平均值。

  • 当使用像素区域插值方法进行放大图像时

    • 如果图像放大的比例是整数倍，那么其工作原理与最近邻插值类似；
    • 如果放大的比例不是整数倍，那么就会调用双线性插值进行放大。

其中目标像素点与原图像的像素点的对应公式如下所示：
s r c X = d s t X ∗ s r c W i d t h d s t W i d t h s r c X=d s t X*{\frac{s r c W i d t h}{d s t W i d t h}} srcX=dstX∗dstWidthsrcWidth

s r c Y = d s t Y ∗ s r c H e i g h t d s t H e i g h t s r c Y=d s t Y*{\frac{s r c H e i g h t}{d s t H e i g h t}} srcY=dstY∗dstHeightsrcHeight

示例代码：

python 复制代码 
import cv2 as cv
#读图
cat = cv.imread("../images/1.jpg")
#获取旋转矩阵
M = cv.getRotationMatrix2D((cat.shape[1]//2,cat.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]))
cv.imshow("dst",dst)
#像素区域插值 缩小：均值滤波 ，放大：整数（最近邻）非整数（双线性，4点，2×2）
dst3 = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]),cv.INTER_AREA)
cv.imshow("dst3",dst3)
cv.waitKey(0)
cv.destroyAllWindows()

4.双三次插值（CV.INTER_CUBIC）

与双线性插值法相同，该方法也是通过映射，在映射点的邻域内通过加权来得到放大图像中的像素值。不同的是，双三次插值法需要原图像中近邻的16个点来加权,也就是4x4的网格。

目标像素点与原图像的像素点的对应公式如下所示：
s r c X = d s t X ∗ s r c W i d t h d s t W i d t h s r c X=d s t X*{\frac{s r c W i d t h}{d s t W i d t h}} srcX=dstX∗dstWidthsrcWidth

s r c Y = d s t Y ∗ s r c H e i g h t d s t H e i g h t s r c Y=d s t Y*{\frac{s r c H e i g h t}{d s t H e i g h t}} srcY=dstY∗dstHeightsrcHeight

下面我们举例说明，假设原图像A大小为m*n，缩放后的目标图像B的大小为M*N。其中A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一个像素点（X,Y）的值，必须先找出像素（X,Y）在原图像A中对应的像素（x,y），再根据原图像A距离像素（x,y）最近的16个像素点作为计算目标图像B（X,Y）处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素（x,y）的值就等于16个像素点的加权叠加。

示例代码：

python 复制代码 
import cv2 as cv
#读图
cat = cv.imread("../images/1.jpg")
#获取旋转矩阵
M = cv.getRotationMatrix2D((cat.shape[1]//2,cat.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]))
cv.imshow("dst",dst)
#双三次插值 16矩阵，4×4
dst4 = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]),cv.INTER_CUBIC)
cv.imshow("dst4",dst4)
cv.waitKey(0)
cv.destroyAllWindows()

5.Lanczos插值（ CV.INTER_LANCZOS4）

Lanczos插值方法与双三次插值的思想是一样的，不同的就是其需要的原图像周围的像素点的范围变成了8*8，并且不再使用BiCubic函数来计算权重，而是换了一个公式计算权重。

首先还是目标像素点与原图像的像素点的对应公式如下所示：
s r c X = d s t X ∗ s r c W i d t h d s t W i d t h s r c X=d s t X*{\frac{s r c W i d t h}{d s t W i d t h}} srcX=dstX∗dstWidthsrcWidth

s r c Y = d s t Y ∗ s r c H e i g h t d s t H e i g h t s r c Y=d s t Y*{\frac{s r c H e i g h t}{d s t H e i g h t}} srcY=dstY∗dstHeightsrcHeight

下面我们举例说明，假设原图像A大小为m*n，缩放后的目标图像B的大小为M*N。其中A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一个像素点（X,Y）的值，必须先找出像素（X,Y）在原图像A中对应的像素（x,y），再根据原图像A距离像素（x,y）最近的64个像素点作为计算目标图像B（X,Y）处像素值的参数，利用权重函数求出64个像素点的权重，图B像素（x,y）的值就等于64个像素点的加权 叠加。

示例代码：

python 复制代码 
import cv2 as cv
#读图
cat = cv.imread("../images/1.jpg")
#获取旋转矩阵
M = cv.getRotationMatrix2D((cat.shape[1]//2,cat.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]))
cv.imshow("dst",dst)
#Lanczos 64矩阵 8×8
dst5 = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]),cv.INTER_LANCZOS4)
cv.imshow("dst3",dst5)
cv.waitKey(0)
cv.destroyAllWindows()

最近邻插值的计算速度最快，但是可能会导致图像出现锯齿状边缘和失真，效果较差。双线性插值的计算速度慢一点，但效果有了大幅度的提高，适用于大多数场景。双三次插值、Lanczos插值的计算速度都很慢，但是效果都很好。

在OpenCV中，关于插值方法默认选择的都是双线性插值，且一般情况下双线性插值已经能满足大部分需求。

二、图像边缘填充的实用方法

在进行仿射变换后的图片会出现黑色部分时我们边需要边缘填充方法使得到的图像更加完整，下面我讲介绍五种边缘填充的方法

1.边界复制（BORDER_REPLICATE）

复制代码 
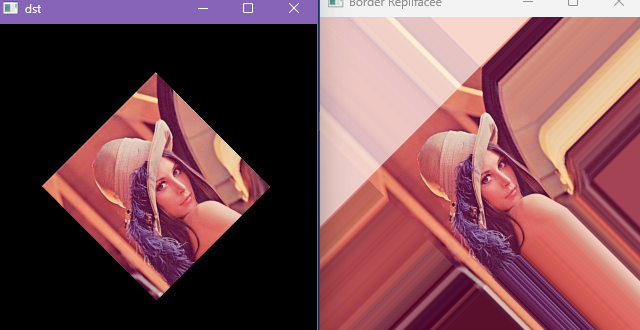
new_img=cv.warpAffine(img,M,(w,h),cv.INTER_LANCZOS4,borderMode=cv.BORDER_REPLICATE)

边界复制会将边界处的像素值进行复制，然后作为边界填充的像素值，如下图所示，可以看到四周的像素值都一样我将结合上述的差值方法结合使用讲解。

示例代码：

python 复制代码 
import cv2 as cv

#读图
face = cv.imread("../images/face.png")
#获取旋转矩阵
M = cv.getRotationMatrix2D((face.shape[1]//2,face.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(face,M,(face.shape[1],face.shape[0]))
cv.imshow("dst",dst)
#最近邻插值 - 边界复制
dst1 = cv.warpAffine(face,M,(face.shape[1],face.shape[0]),cv.INTER_NEAREST,borderMode=cv.BORDER_REPLICATE)
cv.imshow("Border Replifacee",dst1)
cv.waitKey(0)
cv.destroyAllWindows()

执行效果：

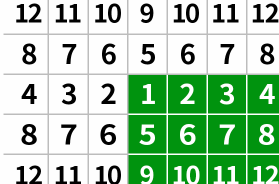
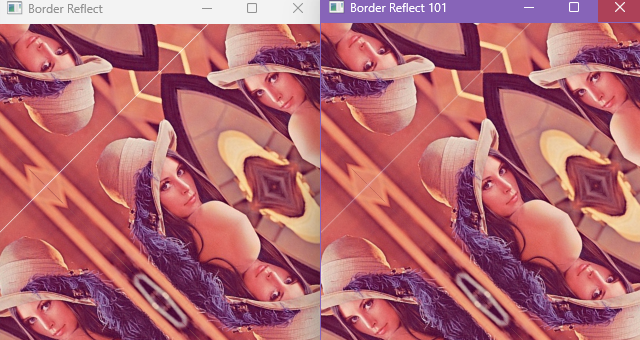
2.边界反射（BORDER_REFLECT）和边界反射101（BORDER_REFLECT_101）

  • 边界反射会根据原图的边缘进行反射。

    new_img=cv.warpAffine(img,M,(w,h),cv.INTER_LANCZOS4,borderMode=cv.BORDER_REFLECT)

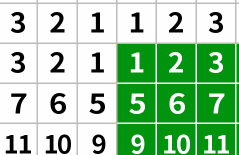
  • 边界反射101和边界反射类似只不过反射是边缘作为零界不会向外反射：

    new_img=cv.warpAffine(img,M,(w,h),cv.INTER_LANCZOS4,borderMode=cv.BORDER_REFLECT_101)

示例代码：

python 复制代码 
import cv2 as cv

#读图
face = cv.imread("../images/face.png")
#获取旋转矩阵
M = cv.getRotationMatrix2D((face.shape[1]//2,face.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(face,M,(face.shape[1],face.shape[0]))
cv.imshow("dst",dst)
#双线性插值 单线性插值，插两次，水平垂直 - 边界反射
dst2 = cv.warpAffine(face,M,(face.shape[1],face.shape[0]),cv.INTER_LINEAR,borderMode=cv.BORDER_REFLECT)
cv.imshow("Border Reflect",dst2)
#像素区域插值 缩小：均值滤波 放大：整数（最近邻）非整数（双线性，4点，2×2）- 边界反射101
dst3 = cv.warpAffine(face,M,(face.shape[1],face.shape[0]),cv.INTER_AREA,borderMode=cv.BORDER_REFLECT_101)
cv.imshow("Border Reflect 101",dst3)
cv.waitKey(0)
cv.destroyAllWindows()

执行效果：

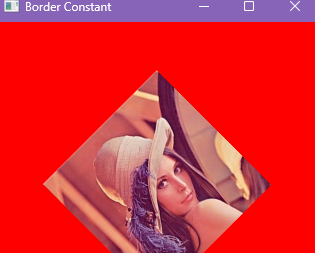
3.边界常数（BORDER_CONSTANT）

当选择边界常数时，还要指定常数值是多少，默认的填充常数值为0，如下图所示。

复制代码 
new_img=cv.warpAffine(img,M,(w,h),cv.INTER_LANCZOS4,borderMode=cv.BORDER_CONSTANT,borderValue=(0,0,255))

示例代码：

python 复制代码 
import cv2 as cv

#读图
face = cv.imread("../images/face.png")
#获取旋转矩阵
M = cv.getRotationMatrix2D((face.shape[1]//2,face.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(face,M,(face.shape[1],face.shape[0]))
cv.imshow("dst",dst)
#双三次插值 16矩阵，4×4 - 边界常数
dst4 = cv.warpAffine(face,M,(face.shape[1],face.shape[0]),cv.INTER_CUBIC,borderMode=cv.BORDER_CONSTANT,borderValue=(0,0,255))
cv.imshow("Border Constant",dst4)
dst3 = cv.warpAffine(face,M,(face.shape[1],face.shape[0]),cv.INTER_AREA,borderMode=cv.BORDER_REFLECT_101)
cv.imshow("Border Reflect 101",dst3)
cv.waitKey(0)
cv.destroyAllWindows()

执行效果：

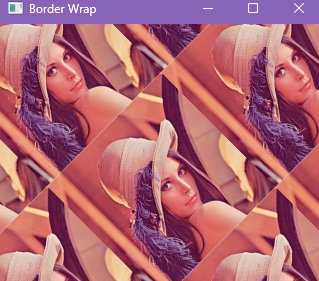
4.边界包裹（BORDER_WRAP）

复制代码 
new_img=cv.warpAffine(img,M,(w,h),cv.INTER_LANCZOS4,borderMode=cv.BORDER_WRAP)

示例代码：

python 复制代码 
import cv2 as cv

#读图
face = cv.imread("../images/face.png")
#获取旋转矩阵
M = cv.getRotationMatrix2D((face.shape[1]//2,face.shape[0]//2),45,0.5)
#仿射变换
dst = cv.warpAffine(face,M,(face.shape[1],face.shape[0]))
cv.imshow("dst",dst)
#Lanczos 64矩阵 8×8 - 边界包裹
dst5 = cv.warpAffine(face,M,(face.shape[1],face.shape[0]),cv.INTER_LANCZOS4,borderMode=cv.BORDER_WRAP)
cv.imshow("Border Wrap",dst5)
cv.waitKey(0)
cv.destroyAllWindows()

执行效果：

三、图像矫正（透视变换）

图像矫正的原理是透视变换，下面来介绍一下透视变换的概念。

听名字有点熟，我们在图像旋转里接触过仿射变换，知道仿射变换是把一个二维坐标系转换到另一个二维坐标系的过程，转换过程坐标点的相对位置和属性不发生变换，是一个线性变换，该过程只发生旋转和平移过程。因此，一个平行四边形经过仿射变换后还是一个平行四边形。

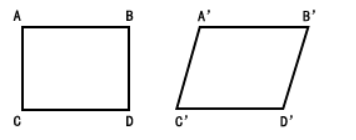
1.透视变换方法

  • M=getPerspectiveTransform(src,dst)

在该函数中，需要提供两个参数：

src：原图像上需要进行透视变化的四个点的坐标，这四个点用于定义一个原图中的四边形区域。

dst：透视变换后，src的四个点在新目标图像的四个新坐标。

该函数会返回一个透视变换矩阵，得到透视变化矩阵之后，使用warpPerspective()函数即可进行透视变化计算，并得到新的图像。该函

数需要提供如下参数：

复制代码 
  cv2.warpPerspective(src, M, dsize, flags, borderMode)

src：输入图像。

M：透视变换矩阵。这个矩阵可以通过getPerspectiveTransform函数计算得到。

dsize：输出图像的大小。它可以是一个Size对象，也可以是一个二元组。

flags：插值方法的标记。

borderMode：边界填充的模式。

复制代码 
原图中卡片的四个角点:左上、右上、左下、右下
[[178, 100], [487, 134], [124, 267], [473, 308]]

示例代码：

python 复制代码 
import cv2 as cv
import numpy as np
#乱码处理

#读图
card = cv.imread("../images/3.png")
shape = card.shape
cv.imshow("card1",card)

#获取透视坐标店:左上，右上，左下，右下
pt1 =  np.float32([[178,100],[487,134],[124,267],[473,308]])
#获取变换后坐标点
pt2 = np.float32([[0,0],[shape[1],0],[0,shape[0]],[shape[1],shape[0]]])
#获取透视变换矩阵
M = cv.getPerspectiveTransform(pt1,pt2)
#透视变换函数cv.warpPerspective(src,M,dsize,flags,borderMode)
dst = cv.warpPerspective(card,M,(shape[1],shape[0]),cv.INTER_LINEAR,borderMode=cv.BORDER_CONSTANT)
cv.imshow("card2",dst)
cv.waitKey(0)
cv.destroyAllWindows()

执行效果：

四、图像掩膜

1.制作掩膜

掩膜（Mask）是一种在图像处理中常见的操作，它用于选择性地遮挡图像的某些部分，以实现特定任务的目标。掩膜通常是一个二值化图像，并且与原图像的大小相同，其中目标区域被设置为1（或白色），而其他区域被设置为0（或黑色），并且目标区域可以根据HSV的颜色范围进行修改

通过这个掩膜，我们就可以对掩膜中的白色区域所对应的原图中的区域进行处理与操作。

复制代码 
  mask=cv.inRange(img,color_low,color_high)

cv2.inRange用于进行多通道图像（尤其是彩色图像）的阈值操作。

示例代码（红，蓝，绿三种颜色举例）：

python 复制代码 
import cv2 as cv
import numpy as np
#乱码处理

#读图
demo = cv.imread("../images/demo.png")
demo = cv.resize(demo,(400,340))
cv.imshow("demo",demo)
#转为hsv颜色空间
hsv = cv.cvtColor(demo,cv.COLOR_BGR2HSV)
#设置颜色阈值
lower_red = np.array([0,43,46])
higher_red = np.array([10,255,255])
#创建掩膜inrange(img,lower_color,higher_color) 函数,传的时hsv颜色空间的图像（二维）
mask = cv.inRange(hsv,lower_red,higher_red)
cv.imshow("red",mask)

lower_blue = np.array([100,43,46])
higher_blue = np.array([124,255,255])
mask1 = cv.inRange(hsv,lower_blue,higher_blue)
cv.imshow("blue",mask1)

lower_green = np.array([35,43,46])
higher_green = np.array([77,255,255])
mask2 = cv.inRange(hsv,lower_green,higher_green)
cv.imshow("green",mask2)
cv.waitKey(0)
cv.destroyAllWindows()

执行效果：

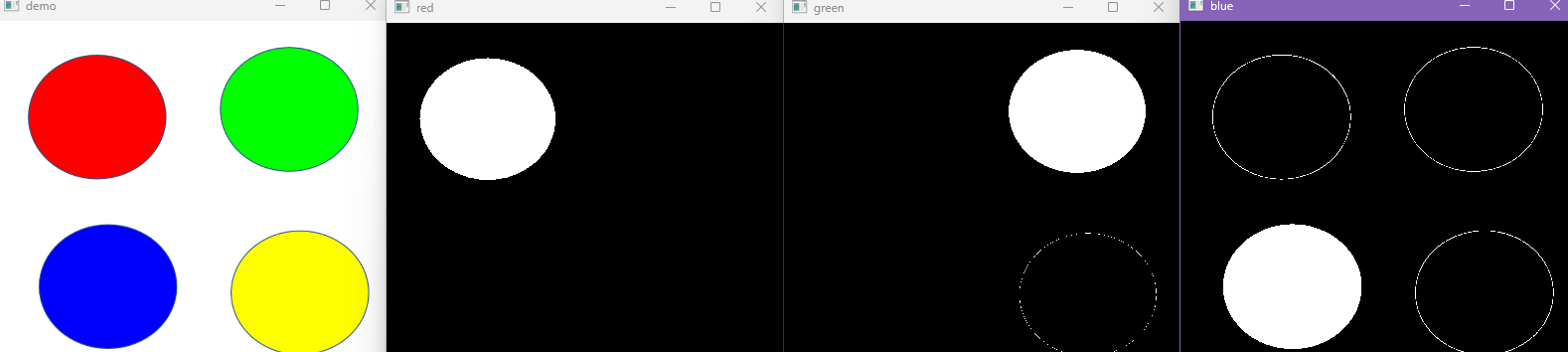
2.颜色提取与替换（与运算）

通过掩膜与原图的与运算，我们就可以提取出图像中被掩膜覆盖的区域(扣图)。

复制代码 
  cv2.bitwise_and(src1,src2[,mask])
  • src1：第一个输入数组。通常是输入的原始图像。
  • src2：第二个输入数组。它可以是另一个图像、一个常数值或者与 src1 相同的图像。
    • 当应用掩膜时，这个参数经常就是src1本身；即对同一个图像进行操作。
    • 如果对两个不同的图像执行按位与操作（例如，将两张图片的某些部分组合在一起），可以分别将它们作为 src1 和 src2 输入到 cv2.bitwise_and() 函数中，创建复杂的图像效果或进行图像合成。
  • mask：掩膜(可选)。输入数组元素只有在该掩膜非零时才被处理。是一个8位单通道的数组，尺寸必须与src1和src2相同。
  • 返回值：输出数组，应用掩膜后的图像，与输入数组大小和类型相同。

示例代码：

python 复制代码 
import cv2 as cv
import numpy as np
#乱码处理

#读图
demo = cv.imread("../images/demo.png")
demo = cv.resize(demo,(400,340))
cv.imshow("demo",demo)
#转为hsv颜色空间
hsv = cv.cvtColor(demo,cv.COLOR_BGR2HSV)
#设置颜色阈值
lower_red = np.array([0,43,46])
higher_red = np.array([10,255,255])
#创建掩膜inrange(img,lower_color,higher_color) 函数,传的时hsv颜色空间的图像（二维）
mask = cv.inRange(hsv,lower_red,higher_red)
cv.imshow("red",mask)
#颜色提取cv.bitwise_and(arc1,arc2[,mask])
dst = cv.bitwise_and(demo,demo,mask = mask)
cv.imshow("red_dst",dst)
cv.waitKey(0)
cv.destroyAllWindows()

运行结果：

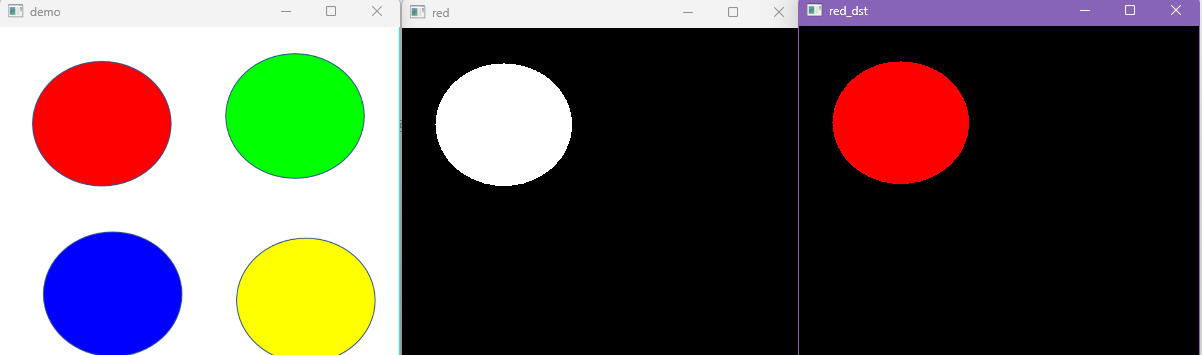
通过上面的步骤实现了颜色的提取

颜色替换

  • mask_image_np == 255 : 这一部分实际上是在生成一个布尔数组，其形状与mask_image_np相同。

  • image_np[...] = (0, 255, 0) : 这里使用了NumPy的高级索引功能。

    示例：

python 复制代码 
import cv2 as cv
import numpy as np
#乱码处理

#读图
demo = cv.imread("../images/demo.png")
demo = cv.resize(demo,(400,340))
cv.imshow("demo1",demo)
#转为hsv颜色空间
hsv = cv.cvtColor(demo,cv.COLOR_BGR2HSV)
#设置颜色阈值
lower_red = np.array([0,43,46])
higher_red = np.array([10,255,255])
#创建掩膜inrange(img,lower_color,higher_color) 函数,传的时hsv颜色空间的图像（二维）
mask = cv.inRange(hsv,lower_red,higher_red)
cv.imshow("red",mask)
#颜色替换，获取布尔数组
arr =mask==255
print(arr)
#图像赋值
demo[arr] = [0,255,0]
cv.imshow("demo2",demo)
cv.waitKey(0)
cv.destroyAllWindows()

执行结果：

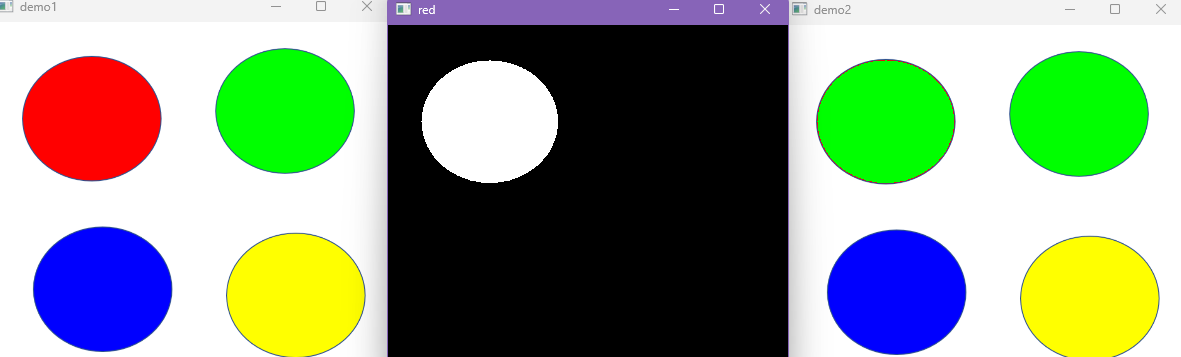
3.图像添加水印

图像添加水印需要三个步骤：图像模板输入，与运算，融合

图像的模板可以通过二值化、图像颜色提取、替换：

python 复制代码 
import cv2 as cv
import numpy as np
#乱码处理

#读图logo和背景
logo = cv.imread("../images/logohq.png")
bg = cv.imread("../images/bg.png")
#获取尺寸
h,w = logo.shape[:2]
roi = bg[:h,:w]
#转灰度图
gray  = cv.cvtColor(logo,cv.COLOR_BGR2GRAY)
#二值化
#黑logo白底
_,mask1 = cv.threshold(gray,200,255,cv.THRESH_BINARY)
bg1 = cv.bitwise_and(roi,roi,mask=mask1)
cv.imshow("bg1",bg1)
#白logo黑底，与上logo
_,mask2 = cv.threshold(gray,200,255,cv.THRESH_BINARY_INV)
logo1 = cv.bitwise_and(logo,logo,mask=mask2)
cv.imshow("mask2",mask2)
cv.imshow("logo1",logo1)
cv.waitKey(0)
cv.destroyAllWindows()

通过与运算依次得到背景黑logo，和logo黑背景，最后通过饱和运算则可以消去两图的黑色部分进行融合实现水印的形成：

python 复制代码 
#融合
#通过赋值运算改变原图像
bg[:h,:w]=cv.add(bg1,logo1)
cv.imshow("roi",roi)
cv.imshow("bg",bg)

五、图像噪点消除

噪声：指图像中的一些干扰因素，通常是由图像采集设备、传输信道等因素造成的，表现为图像中随机的亮度，也可以理解为有那么一些点的像素值与周围的像素值格格不入。常见的噪声类型包括高斯噪声和椒盐噪声。高斯噪声是一种分布符合正态分布的噪声，会使图像变得模糊或有噪点。椒盐噪声则是一些黑白色的像素值分布在原图像中。

滤波与模糊联系与区别：

  • 它们都属于卷积，不同滤波方法之间只是卷积核不同（对线性滤波而言）
  • 低通滤波器是模糊，高通滤波器是锐化
  • 低通滤波器就是允许低频信号通过，在图像中边缘和噪点都相当于高频部分，所以低通滤波器用于去除噪点、平滑和模糊图像。高通滤波器则反之，用来增强图像边缘，进行锐化处理。

注意：椒盐噪声可以理解为斑点，随机出现在图像中的黑点或白点；高斯噪声可以理解为拍摄图片时由于光照等原因造成的噪声。

1.均值滤波（blur）

均值滤波是一种最简单的滤波处理，它取的是卷积核区域内元素的均值，如3×3的卷积核：
k e r n e l = 1 9 [ 1 1 1 1 1 1 1 1 1 ] k e r n e l={\frac{1}{9}}{\Bigg[}\begin{array}{l l l}{1}&{1}&{1}\\{1}&{1}&{1}\\{1}&{1}&{1}\end{array}{\Bigg]} kernel=91[111111111]

示例：

python 复制代码 
#进行降噪处理：均值滤波
dst1 = cv.blur(lvbo2,(3,3))
cv.imshow("dst1",dst1)

2.方框滤波（boxFilter）

方框滤波跟均值滤波很像，如3×3的滤波核如下：
k e r n e l = a [ 1 1 1 1 1 1 1 1 1 ] k e r n e l={a}{\Bigg[}\begin{array}{l l l}{1}&{1}&{1}\\{1}&{1}&{1}\\{1}&{1}&{1}\end{array}{\Bigg]} kernel=a[111111111]

示例：

python 复制代码 
#方框滤波（boxfilter）noramlize=true (均值滤波)
dst2 = cv.boxFilter(lvbo2,-1,(3,3),normalize=False)
cv.imshow("dst2",dst2)

3.高斯滤波（GaussianBlur）

  • 高斯滤波是一种常用的图像处理技术，主要用于平滑图像、去除噪声。它通过使用高斯函数（正态分布）作为卷积核来对图像进行模糊处理。

前面两种滤波方式，卷积核内的每个值都一样，也就是说图像区域中每个像素的权重也就一样。高斯滤波的卷积核权重并不相同：中间像素点权重最高，越远离中心的像素权重越小。还记得我们在自适应二值化里是怎么生成高斯核的吗？这里跟自适应二值化里生成高斯核的步骤是一样的，都是以核的中心位置为坐标原点，然后计算周围点的坐标，然后带入下面的高斯公式中。
g ( x , y ) = 1 2 π σ 2 e − ( x 2 + y 2 ) 2 σ 2 g(x,y)=\frac{1}{2\pi\sigma^{2}}e^{-\frac{(x^{2}+y^{2})}{2\sigma^{2}}} g(x,y)=2πσ21e−2σ2(x2+y2)

其中，x和 y 是相对于中心点的坐标偏移量，σ 是标准差，控制着高斯函数的宽度和高度。较大的 σ 值会导致更广泛的平滑效果。

卷积核通常是一个方形矩阵，其元素值根据高斯函数计算得出，并且这些值加起来等于1，近似于正态分布，以确保输出图像的亮度保持不变。

其中的值也是与自适应二值化里的一样，当时会取固定的系数，当kernel大于7并且没有设置时，会使用固定的公式进行计算 σ \sigma σ的值：
σ = 0.3 ∗ ( ( k s i z e − 1 ) ∗ 0.5 − 1 ) + 0.8 \sigma=0.3*\left((k s i z e-1)*0.5-1\right)+0.8 σ=0.3∗((ksize−1)∗0.5−1)+0.8

我们还是以3*3的卷积核为例，其核值如下所示：
k e r n e l = [ 0.0625 0.125 0.0625 0.125 0.25 0.125 0.0625 0.125 0.0625 ] = [ 1 16 1 8 1 16 1 8 1 4 1 8 1 16 1 8 1 16 ] \ k e r n e l=\left[\begin{array}{c}{{0.0625~~~~0.125~~~~0.0625}}\\{{0.125~~~~0.25~~~~0.125}}\\{{0.0625~~~~0.125~~~~0.0625}} \end{array}\right]=\left[\begin{array}{c c c}{\frac{1}{16}~~~\frac{1}{8}~~~\frac{1}{16}}\\{\frac{1}{8}~~~\frac{1}{4}~~~\frac{1}{8}}\\{\frac{1}{16}~~~\frac{1}{8}~~~\frac{1}{16}}\end{array}\right] kernel= 0.0625 0.125 0.06250.125 0.25 0.1250.0625 0.125 0.0625 = 161 81 16181 41 81161 81 161

得到了卷积核的核值之后，其滤波过程与上面两种滤波方式的滤波过程一样，都是用卷积核从图像左上角开始，逐个计算对应位置的像素值，并从左至右、从上至下滑动卷积核，直至到达图像右下角，唯一的区别就是核值不同。

示例：

python 复制代码 
#高斯滤波GaussianBlur
dst3 = cv.GaussianBlur(lvbo2,(3,3),1)
cv.imshow("dst3",dst3)

4.中值滤波（medianBlur）

中值又叫中位数，是所有数排序后取中间的值。中值滤波没有核值，而是在原图中从左上角开始，将卷积核区域内的像素值进行排序，并选取中值作为卷积核的中点的像素值

示例：

python 复制代码 
#中值滤波：medianBlur
dst4 = cv.medianBlur(lvbo3,3)
cv.imshow("dst4",dst4)

注意：在滤波算法组件中，当参数filtering_method选为中值滤波，参数component_param为ksize，代表卷积核的大小，eg：ksize=3，则代表使用3×3的卷积核。

5.双边滤波（bilateralFilter）

双边滤波采用了两个高斯滤波 的结合，一个负责计算空间邻近度的权值（也就是空域信息），也就是上面的高斯滤波器，另一个负责计算像素值相似度的权值（也就是值域信息），也是一个高斯滤波器。其公式如下所示：
g ( i , j ) = ∑ ( k , l ) ∈ S ( i , j ) f ( k , l ) ω ( i , j , k , l ) Σ ( k , l ) ∈ S ( i , j ) ω ( i , j , k , l ) g(i,j)=\frac{\sum_{(k,l)\in S(i,j)}f(k,l)\omega(i,j,k,l)}{\Sigma_{(k,l)\in S(i,j)}\omega(i,j,k,l)} g(i,j)=Σ(k,l)∈S(i,j)ω(i,j,k,l)∑(k,l)∈S(i,j)f(k,l)ω(i,j,k,l)

  • 分子 ： ∑ ( k , l ) ∈ S ( i , j ) f ( k , l ) ω ( i , j , k , l ) ∑(k,l)∈S(i,j)f(k,l)ω(i,j,k,l) ∑(k,l)∈S(i,j)f(k,l)ω(i,j,k,l)

    • 这是对邻域内所有像素值 f ( k , l ) f(k,l) f(k,l)与其对应的权重 ω ( i , j , k , l ) ω(i,j,k,l) ω(i,j,k,l)的乘积求和。这一步计算了加权后的像素值总和。

  • 分母 ： ∑ ( k , l ) ∈ S ( i , j ) ω ( i , j , k , l ) ∑(k,l)∈S(i,j)ω(i,j,k,l) ∑(k,l)∈S(i,j)ω(i,j,k,l)

    • 这是对邻域内所有像素的权重 ω(i,j,k,l) 求和。这一步计算了权重的总和。

  • 计算过程：

    1. 确定邻域 ：选择一个以 (i,j) 为中心的邻域 为中心的邻域 为中心的邻域 S(i,j)。
    2. 计算权重 ：对于邻域内的每个像素 ( k , l ) (k,l) (k,l)，计算其权重 ω(i,j,k,l)。
    3. 加权求和 ：将邻域内每个像素值 f ( k , l ) f(k,l) f(k,l) 与其权重 ω ( i , j , k , l ) ω(i,j,k,l) ω(i,j,k,l)相乘，并对所有乘积求和。
    4. 归一化 ：将加权求和的结果除以权重总和，得到最终的像素值 g ( i , j ) g(i,j) g(i,j)。
      示例：
python 复制代码 
#双边滤波：bilateralFilter
dst5 = cv.bilateralFilter(lvbo2,9,75,75)
cv.imshow("dst5",dst5)

完整代码如下：

python 复制代码 
import cv2 as cv
import numpy as np
#乱码处理

#读图logo和背景
lvbo2 = cv.imread("../images/lvbo2.png")
#椒盐噪声
lvbo3 = cv.imread("../images/lvbo3.png")
lvbo2 = cv.resize(lvbo2,(330,240))
lvbo3 = cv.resize(lvbo3,(330,240))
cv.imshow("lvbo2",lvbo2)
cv.imshow("lvbo3",lvbo3)
#进行降噪处理：均值滤波
dst1 = cv.blur(lvbo2,(3,3))
cv.imshow("dst1",dst1)

#方框滤波（boxfilter）noramlize=true (均值滤波)
dst2 = cv.boxFilter(lvbo2,-1,(3,3),normalize=False)
cv.imshow("dst2",dst2)

#高斯滤波GaussianBlur
dst3 = cv.GaussianBlur(lvbo2,(3,3),1)
cv.imshow("dst3",dst3)
#中值滤波：medianBlur
dst4 = cv.medianBlur(lvbo3,3)
cv.imshow("dst4",dst4)
#双边滤波：bilateralFilter
dst5 = cv.bilateralFilter(lvbo2,9,75,75)
cv.imshow("dst5",dst5)
cv.waitKey(0)
cv.destroyAllWindows()

运行结果：

小结：

在不知道用什么滤波器好的时候，优先高斯滤波，然后均值滤波。

斑点和椒盐噪声优先使用中值滤波。

要去除噪点的同时尽可能保留更多的边缘信息，使用双边滤波。

线性滤波方式：均值滤波、方框滤波、高斯滤波（速度相对快）。

非线性滤波方式：中值滤波、双边滤波（速度相对慢）。

结语

掌握这些进阶预处理技术，您将能应对绝大多数计算机视觉项目中的图像处理挑战。本文不仅提供了可直接复用的代码方案，更揭示了各种方法背后的设计思想，帮助您根据具体场景灵活选择最优解。

🔧 动手实验建议： 尝试为一批不同角度的商品照片设计自动矫正流程，并添加具有抗攻击能力的企业水印。

相关推荐
弥金6 分钟前
LangChain基础
人工智能·后端
不摸鱼17 分钟前
创业找不到方向？不妨从行业卧底开始 | 不摸鱼的独立开发者日报（第66期）
人工智能·开源·资讯
ReinaXue17 分钟前
大模型【进阶】（五）：低秩适配矩阵LORA的深度认识
人工智能·深度学习·神经网络·语言模型·自然语言处理·transformer
牵牛老人18 分钟前
OpenCV学习探秘之二 ：数字图像的矩阵原理，OpenCV图像类与常用函数接口说明，及其常见操作核心技术详解
opencv·学习·矩阵
人生都在赌19 分钟前
AI Agent从工具到生态的秘密：我们踩过的坑和3个月实践教训
人工智能·ci/cd·devops
北极的树24 分钟前
大模型上下文工程之Prefix Caching技术详解
人工智能·ai编程
奇舞精选25 分钟前
prompt的参数调优入门指南 - 小白也能轻松掌握
人工智能·aigc
DisonTangor25 分钟前
商汤InternLM发布最先进的开源多模态推理模型——Intern-S1
人工智能·深度学习·开源·aigc
wayman_he_何大民26 分钟前
RAG系统架构：让AI学会"查资料"的魔法
人工智能
泽安AI研习社27 分钟前
Coze 开源了，送上保姆级私有化部署方案【建议收藏】
人工智能
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02全球最强模型Grok4，国内已可免费使用！（附教程）03vue数据变化但页面不变04KGG转MP3工具|非KGM文件|解密音频05干翻 Typora！MilkUp：完全免费的桌面端 Markdown 编辑器！06扣子开源本地部署教程 丨Coze智能体小白喂饭级指南07【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致08ChatGPT Agent 完全使用指南：2025年7月最新功能详解09《魔兽世界》提示lua警告的含义及解决方法10这次领先Cursor！体验了Trae 2.0 SOLO 模式，超酷！