马尔可夫模型是一种随机过程,具有以下特性:
马尔可夫性:
对于任意状态序列 S1,S2,...,Sn,满足:
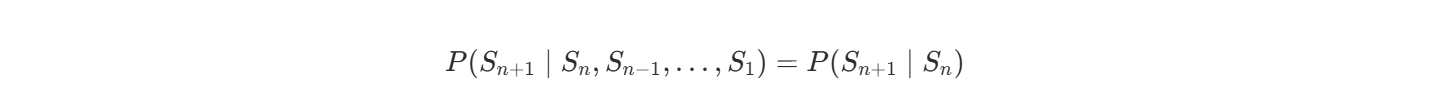
也就是说,下一步的状态只和当前状态有关,而与之前的历史无关。
一阶马尔可夫模型 ,在语言建模里叫 Bigram Model。
例如:我 今天 下午 打 篮球
P(我 今天 下午 打 篮球)
≈P(今天∣我)⋅P(下午∣今天)⋅P(打∣下午)⋅P(篮球∣打)
P(今天∣我)=Count(我,今天)/Count(我)
P(下午∣今天)=Count(今天,下午)/Count(今天)
P(打∣下午)=Count(下午,打)/Count(下午)
P(篮球∣打)=Count(打,篮球)/Count(打)
一、N-gram 模型
| 方面 | 马尔可夫 | N-gram |
|---|---|---|
| 定义 | 一种概率模型理论,假设有限历史依赖 | 马尔可夫模型在自然语言建模中的实现 |
| 适用领域 | 广泛(语言、天气、游戏、金融等) | 主要是 NLP(语言建模、文本生成等) |
| 依赖范围 | 依赖前 N−1 个状态(N 阶) | 依赖前 N−1 个词(n 阶) |
| 举例 | 一阶马尔可夫预测明天天气 | Bigram 预测下一个词 |
| 数学关系 | N-gram = N-1 阶马尔可夫在文本上的应用 | ------ |
1.1 N-gram 模型概念
N-gram 模型是一种 基于概率的语言模型,用来预测一个词(或符号)在序列中出现的可能性。它的核心思想是:
当前词的出现只依赖于前面 n−1 个词(马尔可夫假设)。
- N-gram :指由连续的 n 个词(或符号)组成的序列。
- n=1 → Unigram(单词单独看)
- n=2 → Bigram(成对的词)
- n=3 → Trigram(三连词)
- 以此类推...
- 模型目标:用 N-gram 的统计概率来近似真实的语言分布。
在 NLP 里,N-gram 就是把句子分成 N 个连续的 token 组合来建模。
-
Bigram(n=2) → 对应一阶马尔可夫Bigrams(当前词只依赖前一个词):

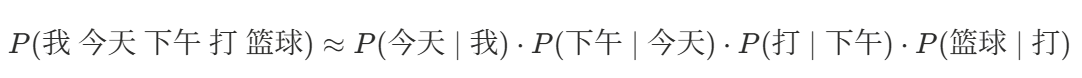
-
Trigram(n=3) → 对应二阶马尔可夫Trigrams(当前词依赖前两个词):


1.2 优缺点
优点
- 简单易实现,统计计算直接。
- 对小规模语料效果还可以。
- 曾经是机器翻译、语音识别的主力模型。
缺点
- 需要大量语料才能得到稳定的概率(稀疏问题)。
- 无法处理超长距离依赖(只看 n−1 个词)。
- 随着 n 增加,参数量爆炸,存储和计算成本高。
- 为解决稀疏问题,提出了 平滑(Smoothing) 方法,如 Laplace、Kneser--Ney 平滑。
- 现代 NLP 基本用 神经网络语言模型 (如 LSTM、Transformer)替代 N-gram,因为它们能捕捉更长的依赖关系,并且不用存储全部 n-gram 组合。