数学建模——线性规划类题目（运筹优化类）

**萌新自用**

1.概念

数学建模中的线性规划类题目 是一类典型的优化问题，

其目标是在一组线性约束条件 下，求一个线性目标函数的最大值或最小值。

常见类型有：生产产品类，车辆规划类，投资类

题目一般是在有限的资源获得最大的收益，而且只有线性函数

例：某工厂生产产品P和Q，利润分别为3元和4元。

P需2小时机加工 + 4小时装配
Q需3小时机加工 + 2小时装配

每天机加工最多16小时，装配最多22小时。问如何安排生产使利润最大？

2.三要素

决策变量：表示你想优化的量（如生产数量、资源分配等）。
目标函数：你希望最大化或最小化的线性函数，如利润、成本、时间等。
约束条件：由线性不等式或等式组成，表示资源限制、技术条件等。
非负约束：决策变量一般要求非负。

3.关于linprog函数

公式格式：

Matlab 复制代码

[x, fval, exitflag, output] = linprog(f, A, b, Aeq, beq, lb);

1.参数：

|------|--------------------------------|
| 参数位置 | 含义 |
| f | 目标函数系数向量（列向量） |
| A | 不等式约束矩阵（左侧系数） |
| b | 不等式约束右侧常数向量 |
| Aeq | 等式约束矩阵（Aeq），空表示无等式约束 |
| beq | 等式约束右侧常数向量（beq），空表示无等式约束 |
| lb | 变量下界（lower bound） |
| ub | 变量上界（upper bound） |

2.函数的返回值（一般只要前两个，你写几个它就给你几个）

|--------------|--------------------|--------|-------------------------------------------------------|
| 返回值 | 含义 | 类型 | 举例/备注 |
| x | 最优解向量 | 列向量 | 如 [2.5; 3.5] 表示决策变量的最优取值 |
| fval | 最优目标函数值 | 标量 | 因为 linprog 只能求 min ，如果你原问题是 max ，需要再乘以 -1 |
| exitflag | 算法终止状态码 | 整数 | 1 表示收敛到最优解，其他值见下表 |
| output | 结构体，包含迭代次数、算法类型等信息 | struct | output.iterations、output.algorithm |

4. 线性规划的表现形式

1.一般形式/代数形式(就是目标+约束+非负)

2.简写

3*.矩阵表现形式（matlab写法）

Matlab 复制代码

f = [-3; -4];           % 目标函数系数（注意是min问题，取负）
A = [2 3; 4 2];         % 约束系数矩阵
b = [16; 22];           % 约束右侧值
lb = [0; 0];            % 非负约束

[x, z] = linprog(f, A, b, [], [], lb);

5.解题步骤

|---------------|------------------|-------------------------------|
| 步骤 | 内容 | 示例说明 |
| 1. 读题理解 | 明确问题背景、优化目标和限制条件 | 如"最大化利润"、"最小化成本"，明确要找的是最大还是最小 |
| 2. 确定决策变量 | 用符号表示待优化的变量 | 如设 x 为产品A的产量，y 为产品B的产量 |
| 3. 建立目标函数 | 用变量表示你想最大化或最小化的量 | 如 maxZ=3x+4y（利润） |
| 4. 列出约束条件 | 把题目中的限制翻译成线性不等式 | 如 2x+3y≤16（机器时间限制） |
| 5. 添加非负约束 | 所有变量 ≥ 0 | x≥0,y≥0 |

6.解决问题

题目：某工厂生产产品P和Q，利润分别为3元和4元。

P需2小时机加工 + 4小时装配
Q需3小时机加工 + 2小时装配

每天机加工最多16小时，装配最多22小时。问如何安排生产使利润最大？

建模如下：

决策变量 ：

x：产品P的生产数量

y：产品Q的生产数量
目标函数（最大化利润）：
约束条件（资源限制）：

完整基础代码：

Matlab 复制代码

% 目标系数（注意是 min，所以取负）
f = [-3; -4];

% 不等式约束 A·x ≤ b
A = [2 3;
     4 2];
b = [16; 22];

% 变量下界
lb = [0; 0];

% 求解
[x_opt, profit_neg] = linprog(f, A, b, [], [], lb);

% 还原最大利润
profit = -profit_neg;

fprintf('最优产量：P = %.2f, Q = %.2f\n', x_opt(1), x_opt(2));
fprintf('最大利润：%.2f 元\n', profit);

补充：注意点：

因为 linprog 只能做 min，把目标函数乘 -1 即可。遇到min问题不动，直接写系数。遇到max问题要把系数乘以-1。

解释：因为 linprog 只能求最小值（min） ，而你建模的目标是 "最大化利润" （max），所以需要把目标函数 乘以 -1 来"骗" MATLAB 去求最小值。

原始目标函数（你想最大化利润）：max Z = 3x₁ + 4x₂

但 linprog 只认：min Z' = fᵀx

所以我们把目标函数 乘以 -1 ：min Z' = -3x₁ - 4x₂

这样 linprog 求出的最小值其实是 负的最大利润：

profit_neg 就是 -Z_max
所以 还原真实最大利润 要再取负号

2.约束矩阵写法：约束系数矩阵和约束右侧值分开写 ，其中约束右侧值每一个值都是拿分号隔开 3.约束矩阵默认处理小于等于符号，大于等于需要手动加上负号，非负约束矩阵要单独写。

就算没有系数也要用0代替

3.代码运行失败原因：

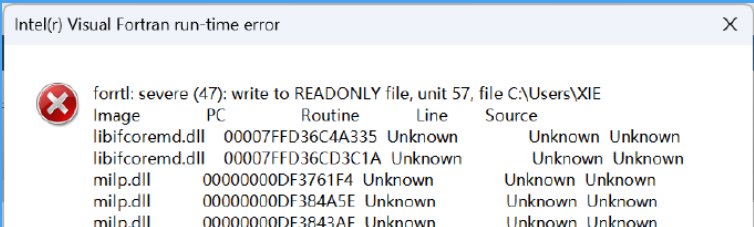
尝试用管理员身份运行

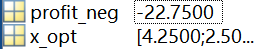
7.真题（1998A）

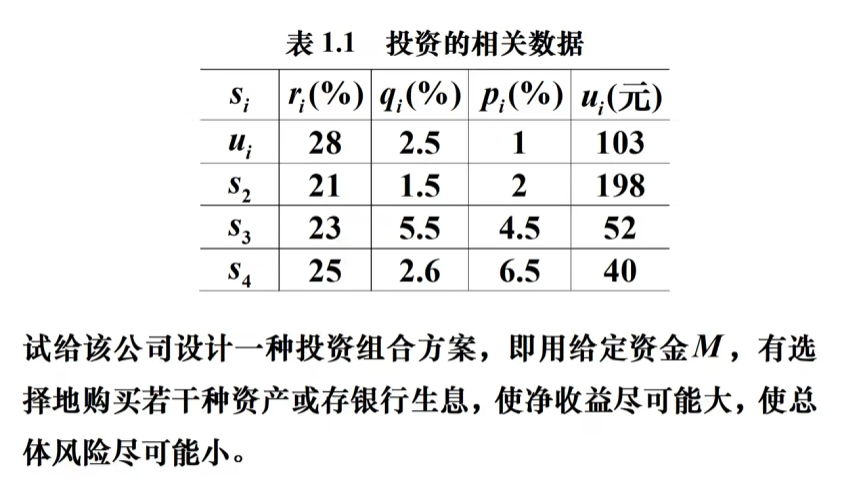
问题分析：

1.决策变量：投资不同项目si的为xi（i=1，2...n）

2.目标函数：有两个（净收益尽可能大，总风险尽可能小）

3.约束条件：总资金M有限，投资是非负数，且目标函数和约束条件都是决策变量的线性函数

模型假设：

1.投资数额M相当大

2.投资越分散，总的风险越小，总体风险可用所投资的si中最大的一个风险来度量

3.可供选择的n+1种资产（含银行存款）之间是相互独立的

4.每种资产的购买量可以是任意值

5.在当前投资周期内，ri，qi，pi，ui固定不变

6.不考虑资产交易过程中产生的其他费用

7.由于投资数额M相当大，而题目中设定的定额ui相对M很小，pi，ui更小，假设每一笔交易xi都大于对应定额ui

模型建立：

总体风险用所投资的si中最大的一个风险来衡量，即

购买资产所用的交易费计算函数本来是一个分段函数，但是已经假设每一笔交易都大于定额，所以交易费是,这样净收益可以简化为

|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 目标函数 | 约束条件 |
| | |

多目标模型简化：

在实际投资中，投资者承受风险的程度不一样，如果给定风险一个界限a，使最大的一个风险,可以找到相应的投资方案，把多目标变成单个目标的线性规划

1.风险率不超过某个定值

2.投资金额等于总资产

3.投资金额都是非负数

|-------------------------------------------------------------------|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 目标函数 | 约束条件 |
| | |

实操：

代码：

Matlab 复制代码

clc,clear;
a=(0:0.001:0.05);%表示不同风险率，步长是0.001
f=[-0.05,-0.27,-0.19,-0.185,-0.185];%总收益
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];%对角矩阵
Aeq=[1,1.01,1.02,1.045,1.065];%等式约束矩阵
beq=1;
lb=zeros(5,1);%下限矩阵
Q=zeros(1,length(a));%最优解矩阵
XX=[];%存储不同风险上限下的最小值
for i=1:length(a)
    b=a(i)*ones(4,1);
    [x,y]=linprog(f,A,b,Aeq,beq,lb);
    Q(i)=-y;
    XX=[XX;x'];%'表示取转置，追加在原来矩阵的下面
end
plot(a,Q,'*r');
xlabel('风险率');
ylabel('最大收益');
XX(7,:)
XX(26,:)