本篇参考周志华老师的西瓜书，但是本人学识有限仅能理解皮毛，如有错误诚请读友评论区指正，万分感谢。
二、核心算法与模型
2.1线性模型
2.1.1、线性模型基本形式（3.1节）
1. 数学形式
-
样本表示：x=(x1;x2;... ;xd)（含 d个属性）
-
预测函数：
-
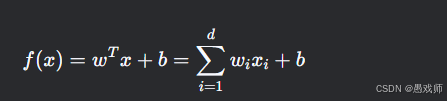
w=(w1;w2;... ;wd)：权重向量，决定各属性对预测的影响方向与强度。
-
b：偏置项，补偿样本均值与真实标记的偏差。
-
2. 核心特点
-
可解释性 ：权重 wi的绝对值大小直接反映属性重要性（如
表示根蒂对判断西瓜好坏更关键）。 -
基础性 ：线性决策边界
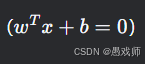是复杂模型（如神经网络、SVM）的基本组件。
2.1.2、线性回归（3.2节）
线性回归用于预测连续值输出，目标是学得最优参数w和b，使模型对训练数据的预测尽可能接近真实标记。
1. 问题定义
-
目标 ：学习参数 w,b 使得预测值
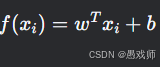逼近真实连续值 。
-
损失函数：均方误差（MSE）
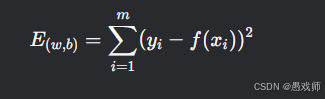
选择理由：
-
几何意义：最小化预测值与真实值的欧氏距离。
-
数学性质 ：严格凸函数，存在唯一全局最小值。
-
概率解释 ：假设噪声
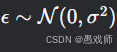时，MSE 等价于高斯噪声下的极大似然估计（MLE）。
-
2. 优化方法：最小二乘法
(1) 单变量情形（1个属性）
-
闭式解：
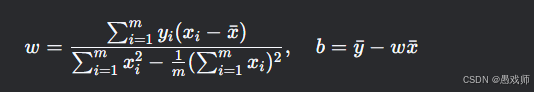
斜率 w 可进一步化为协方差和方差的比值形式，见下述推导过程。
-
推导 ：对
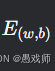求偏导并令导数为零：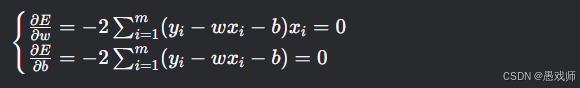
接下来简单解释一下数学原理：
-
几何意义：直线穿过所有样本点的"中心" (xˉ,yˉ)，且斜率 w 由协方差和方差的比值决定。
-
优化策略：最小二乘法 通过求导得正规方程 ，直接求解最优参数（闭式解）。
(2) 多元情形（d个属性）
-
参数合并 ：
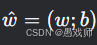，样本矩阵 X 添加全1列（对应偏置 b）。 -
损失函数矩阵形式：
-
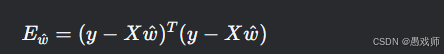
最优解：
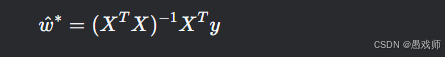
推导：
简单来说： 最小二乘法通过巧妙地设计矩阵
X和参数向量ŵ，把多元线性回归的"找最优直线/超平面"问题，转化成了一个求解矩阵方程XᵀXŵ = Xᵀy的问题。解这个方程，就找到了让总平方误差最小的那组参数
(3) 解的存在性问题
-
满秩矩阵 ：当
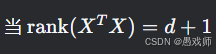时，解唯一。 -
不满秩（属性数 > 样本数）：
-
引入正则化（如 L2 正则化）：
-
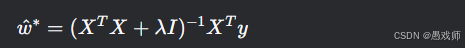
作用：限制参数规模，防止过拟合（几何上压缩解空间）。
-
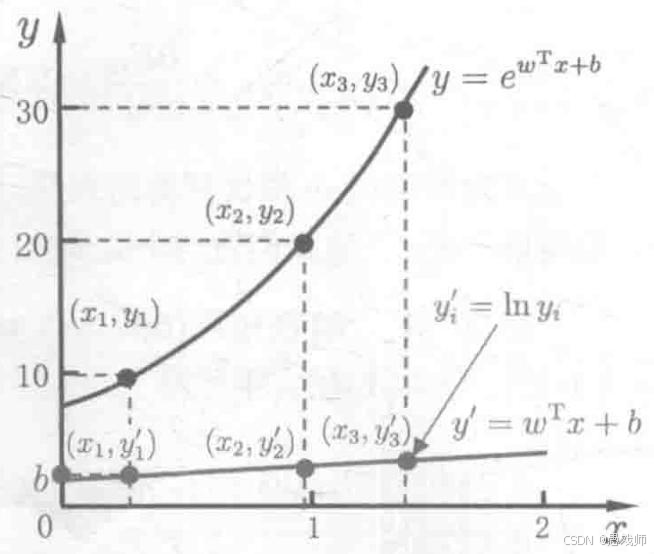
3. 扩展：对数线性回归
-
模型形式：
-
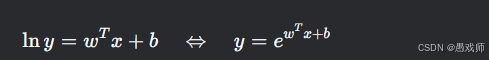
应用场景：输出标记呈指数增长（如人口增长、病毒传播）。
-
本质：将非线性问题转化为线性问题，仍使用最小二乘法求解。
2.1.3、对数几率回归（3.3节）
对数几率回归（logistic regression）虽名为 "回归"，实则是一种二分类学习方法，其核心是通过线性模型结合对数几率函数实现分类，具有可解释性强、能输出概率预测等优点。
基本思路 ：分类任务需将线性回归的实值输出转换为 0/1 类别标记。理想的转换函数是 "单位阶跃函数"，但该函数不连续、不可微，因此采用对数几率函数（logistic function） 作为替代 ------ 这是一种 Sigmoid 函数，能将实值映射到 (0,1) 区间，且单调可微：。其中
为线性回归输出。
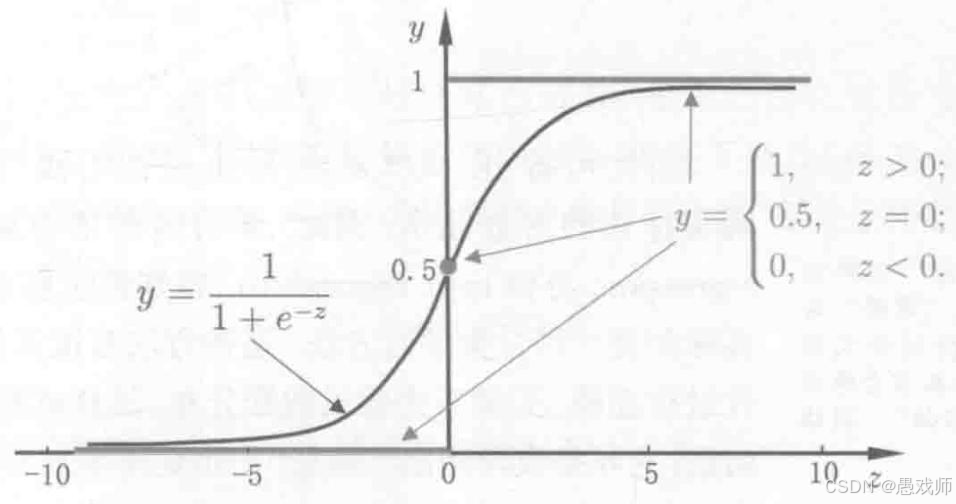
单位阶跃函数与对数几率函数
- 模型表达式 ：将线性回归结果代入对数几率函数，得到：
Q1：为何使用Sigmoid函数？
-
问题 ：线性回归输出
-
解决方案：
-
Sigmoid函数特性：
-
将 (−∞,+∞) 压缩到 (0,1)，满足概率公理
-
单调连续可微（利于优化）
-
临界点 z=0时 y=0.5（天然分类阈值）
-
-
对数几率（Log Odds）
-
定义：
-
物理意义：
-
分子 p(y=1∣x)：正例概率
-
分母 p(y=0∣x)：反例概率
-
比值：正例相对反例的"优势比"（Odds Ratio）
-
-
核心思想 ：用线性模型 直接拟合对数几率 （线性决策边界
损失函数：对数似然损失
- 核心目标 ：最大化 "对数似然"，即使每个样本属于其真实标记的概率最大。 若将y视为样本x为正例的概率
- 对数似然函数：取对数后转化为求和形式，最大化似然等价于最小化以下损失函数：
其中为扩展参数向量，
为扩展样本向量。该函数是关于
的凸函数，可通过凸优化算法求解最优解。
极大似然估计（MLE）推导
-
概率建模：
-
似然函数：
-
负对数似然（NLL）：
这上边写公式太费力了接下来的步骤还是手写吧
损失函数凸性证明
-
关键性质：
-
损失函数 ℓ(β) 是 凸函数
-
Hessian矩阵半正定：
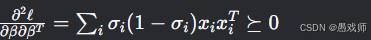
→ 无局部极小值，全局最优解存在
-
交叉熵损失
-
信息论视角：
-
真实分布：[yi,1−yi]（One-Hot编码）
-
预测分布：[σ(zi),1−σ(zi)]
-
-
优化目标：最小化预测概率分布与真实分布的差异（KL散度）
优化方法
由于对数似然损失函数是凸函数，无局部极小值，常用数值优化算法求解参数：
- 梯度下降法 ：通过计算损失函数对
其中为正例概率预测值。
- 牛顿法：利用二阶导数（海森矩阵）加速收敛，迭代更新公式为：
二阶导数为：
梯度下降法（一阶优化）
更新公式：
其中：
-
η：学习率（步长）
-
梯度计算
-
物理意义：
-
-
-
牛顿法（二阶优化）
算法原理
更新公式：
其中海森矩阵：
- 关键组件解析
-
梯度 ：
-
海森矩阵：
-
σi(1−σi)：概率不确定度（在0.5时最大）
-
-
-
矩阵求逆 ：
梯度下降实现：
python
def gradient_descent(X, y, lr=0.01, epochs=1000):
"""
X: 设计矩阵 (m x (d+1))
y: 标签向量 (m x 1)
"""
beta = np.zeros(X.shape[1]) # 初始化参数
for _ in range(epochs):
z = X @ beta # 线性预测
p = 1 / (1 + np.exp(-z)) # Sigmoid
grad = -X.T @ (y - p) # 梯度计算
beta -= lr * grad # 参数更新
return beta牛顿法实现：
python
def newton_method(X, y, max_iter=10):
beta = np.zeros(X.shape[1])
for _ in range(max_iter):
z = X @ beta
p = 1 / (1 + np.exp(-z))
grad = -X.T @ (y - p) # 梯度
# 海森矩阵计算
W = np.diag(p * (1 - p)) # 权重矩阵
H = X.T @ W @ X # 海森矩阵
# 避免奇异矩阵
H_reg = H + 1e-6 * np.eye(H.shape[0])
# 参数更新
beta -= np.linalg.inv(H_reg) @ grad
return beta优化目标与结果
两种方法均以最小化对数似然损失为目标，最终求解得到最优参数：
参数确定后，模型即可通过输出样本为正例的概率，进而完成分类预测。
小结
对数几率回归的优化核心是利用凸函数性质，通过梯度下降或牛顿法求解对数似然损失的最小值。梯度下降实现简单、适合大规模数据；牛顿法收敛更快，但计算成本较高。两种方法均能有效得到最优参数，为模型提供稳定的概率输出和分类能力。
2.2决策树
决策树是一种基于树结构进行决策的机器学习模型，核心思想是 "分而治之"（divide-and-conquer），通过递归划分样本构建树结构，并通过剪枝处理提升泛化能力。本章核心内容包括基本流程、划分选择、剪枝处理。
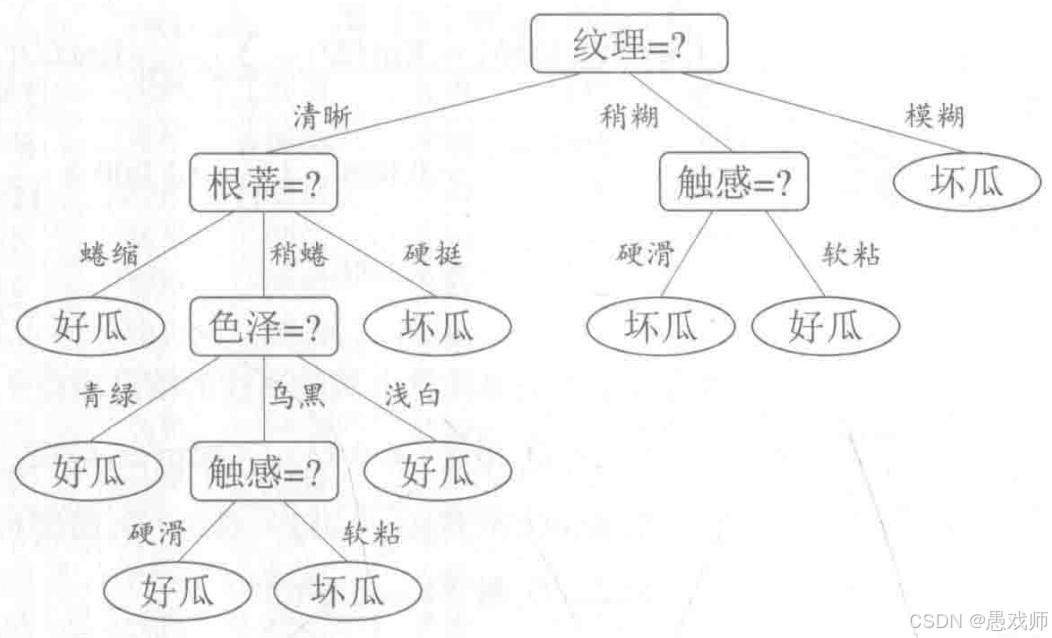
引用自西瓜书
西瓜问题的一棵决策树
2.2.1、决策树基本流程
递归划分样本构建树结构，具体流程如下：
-
核心思想
从根节点（包含所有训练样本）出发，根据某一属性将样本划分为若干子节点；每个子节点对应该属性的一个取值，包含该取值的所有样本；递归执行此过程，直至子节点满足停止条件。
-
递归停止条件
- 当前节点包含的样本全属于同一类别，无需划分，直接标记为该类别的叶节点；
- 可用属性集为空，或所有样本在剩余属性上取值相同，无法划分，将节点标记为所含样本数最多的类别的叶节点；
- 当前节点包含的样本集合为空，不能划分，标记为父节点所含样本数最多的类别的叶节点。
-
结构特点
树由根节点、内部节点（属性测试）和叶节点（决策结果）组成，从根节点到叶节点的路径对应一组决策规则，具有直观的可解释性。
2.2.2、划分选择
划分选择的核心是选择 "最优属性"，使划分后子节点的样本 "纯度"（同类样本集中程度）最高，常用划分准则包括信息增益、增益率和基尼指数。
1. 信息增益
- 信息熵 ：度量样本集合纯度的指标。对于样本集D，若第k类样本占比为
- 信息增益 ：使用属性a划分样本集D后获得的 "纯度提升"。计算公式为
- 应用：信息增益越大，说明该属性划分效果越好。ID3 决策树算法即采用信息增益选择划分属性。
2. 增益率
- 问题背景：信息增益对可取值数目较多的属性有偏好（如 "编号" 这类属性可能获得极高增益但无实际意义）。
- 定义 ：为减少这种偏好，引入 "增益率"，计算公式为
- 应用：C4.5 算法采用增益率，但并非直接选择增益率最大的属性，而是先筛选出信息增益高于平均水平的属性，再从中选择增益率最高的。
3. 基尼指数
- 基尼值 ：度量样本集合纯度的另一种指标，反映随机抽取两个样本类别标记不一致的概率。定义为
- 基尼指数 ：属性a的基尼指数为划分后各子集基尼值的加权和，即
- 应用：CART 决策树选择基尼指数最小的属性作为最优划分属性10。
核心逻辑
划分选择的核心目标是通过属性划分提高结点纯度，不同准则（信息增益、增益率、基尼指数）从不同角度衡量划分效果，分别被 ID3、C4.5、CART 等经典决策树算法采用，以适应不同场景下的纯度优化需求。
2.2.3 剪枝处理
决策树的 "剪枝处理"是应对决策树过拟合的主要手段。剪枝通过主动移除部分分支，降低模型复杂度，提升泛化能力
1. 剪枝的基本思路
决策树在训练过程中可能因过度拟合训练数据（如分支过多）导致泛化能力下降。剪枝通过判断分支划分是否能提升泛化性能，决定是否保留或移除分支，主要分为两种策略：
- 预剪枝：在决策树生成过程中，对每个结点划分前先评估，若划分不能提升泛化性能，则停止划分并将当前结点标记为叶结点。
- 后剪枝：先生成完整决策树，再自底向上考察非叶结点，若将子树替换为叶结点能提升泛化性能，则进行替换。
2. 预剪枝
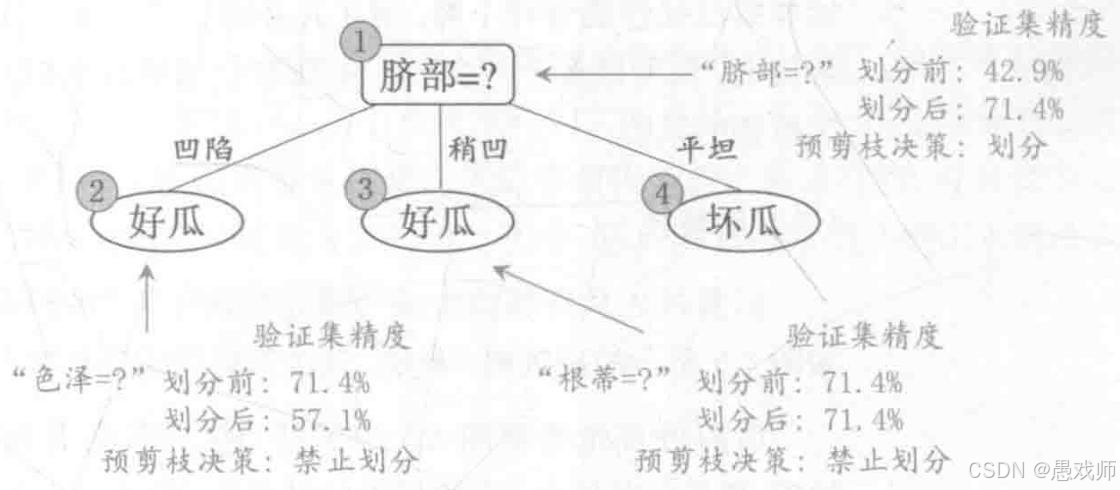
引用自西瓜书
- 核心逻辑：在结点划分前，通过验证集评估划分前后的性能。若划分后验证集精度提升，则执行划分；否则停止划分。
- 示例：以西瓜数据集 2.0 的训练集和验证集为例，根结点若不划分，验证集精度为 42.9%；用 "脐部" 划分后，验证集精度提升至 71.4%，因此确定划分。后续分支若划分后精度未提升（如 "色泽" 划分后精度降至 57.1%），则禁止划分。
- 优缺点：能显著减少决策树分支，降低计算开销，但可能因提前停止划分导致 "欠拟合"。
3. 后剪枝
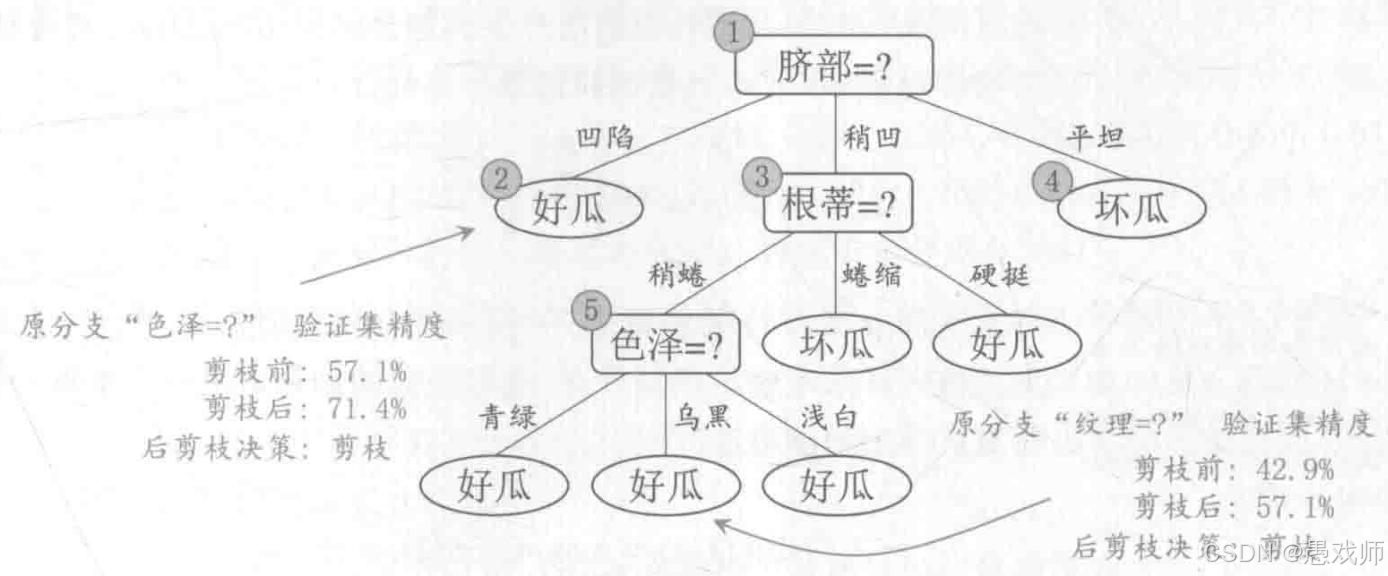
引用自西瓜书
- 核心逻辑：先生成完整决策树，再从叶结点向上回溯，评估将子树替换为叶结点后的验证集性能。若性能提升，则替换。
- 优缺点：泛化性能通常优于预剪枝，但训练时间开销更大（需先生成完整树再迭代剪枝）。
4. 性能评估依据
剪枝效果通过验证集精度判断，即预留部分数据作为验证集，比较划分 / 替换前后模型在验证集上的分类精度，以此确定是否进行剪枝。剪枝的核心是通过控制决策树复杂度平衡 "拟合能力" 与 "泛化能力"，预剪枝高效但可能欠拟合，后剪枝泛化性好但成本较高，实际应用中需根据场景选择。
2.2.4连续属性 和属性值缺失处理方法
1. 连续值处理
- 问题背景：连续属性（如 "密度""含糖率"）的取值是连续区间，无法像离散属性那样直接根据取值划分样本。
- 处理方法 ：
- 确定候选划分点 ：将连续属性的所有取值排序后，取相邻两个值的中点作为候选划分点，即对属性a的取值
- 选择最优划分点：计算每个候选划分点的信息增益（与离散属性的信息增益计算方式类似），选择增益最大的划分点作为该属性的最优划分点。
- 特点：连续属性可作为后代结点的划分属性（如父结点用 "密度≤0.381" 划分后，子结点仍可用 "密度≤0.294" 划分）。
- 确定候选划分点 ：将连续属性的所有取值排序后，取相邻两个值的中点作为候选划分点，即对属性a的取值
2. 缺失值处理
- 问题背景：样本的某些属性值可能缺失（如 "色泽""敲声" 等属性无记录），需解决两个问题：如何选择划分属性？样本属性值缺失时如何划分？
- 处理方法 ：
- 划分属性选择 ：
- 仅基于有完整属性值的样本子集
- 定义无缺失值样本占比
- 仅基于有完整属性值的样本子集
- 样本划分 ：
- 若样本属性值已知，划入对应子结点，权重不变。
- 若样本属性值缺失，同时划入所有子结点，权重按属性取值占比
- 划分属性选择 ：
用个比方解释：
想象一下：你在玩一个猜水果的游戏（决策树），要根据水果的特征（属性）猜它是什么（类别）。但有些水果的标签掉了（属性值缺失），怎么办？
这个处理方法主要解决两个头疼的问题：
-
选哪个特征来猜？ (划分属性选择)
-
标签掉了的水果放哪里？ (样本划分)
1. 选哪个特征来猜？ (处理缺失值后的信息增益计算)
-
问题： 有些水果的"颜色"标签掉了，有些水果的"声音"标签掉了。我们怎么知道用"颜色"还是"声音"来猜水果种类更有效呢？
-
解决方法：
-
只看标签完整的： 先别管那些标签掉了的水果。只把所有标签都完整 的水果（子集
D_hat）拿出来。 -
像平常一样算： 用这些标签完整的水果，像没有缺失值一样，计算用"颜色"猜有多好（
Ent(D_hat)），用"声音"猜有多好（Ent(D_hat)），以及用了"颜色"或"声音"后猜得有多准（Sum(... Ent(D_hat^v))）。这就算出了基于完整样本的信息增益基础值[Ent(D_hat) - Sum(...)]。 -
打个折扣： 但是！因为我们只用了部分水果（标签完整的），没用全部水果。所以这个"猜得有多好"的值要打个折。打折的比例就是 "标签完整的水果占所有水果的比例" (ρ)。
-
最终得分 = 打折后的效果： 真正的"用这个特征猜有多好"（信息增益）就是：
Gain = ρ * [刚才算的基础值]。 -
谁得分高选谁： 比较"颜色"和"声音"最终的这个
Gain分数，谁分数高，说明（在考虑缺失值的情况下）用这个特征来猜更有效，就选谁！
-
简单总结选特征：只看好的水果算效果，算完效果打个折（按好水果的比例），打折后的分数才是真本事。
2. 标签掉了的水果放哪里？ (样本划分)
-
问题： 现在选定用"颜色"来分水果了（比如分成"红"、"绿"、"黄"三个篮子）。但有些水果的颜色标签掉了，该放进哪个颜色的篮子里呢？
-
解决方法：
-
标签没掉的水果： 如果水果的颜色标签还在，比如是"红色"，那就正常放进"红色"的篮子里。它在篮子里的"分量"（权重
w_x）还是 1（或者原来的值）。 -
标签掉了的水果： 如果一个水果的颜色标签掉了，别扔掉它！我们玩个"分身术"：
-
把它同时 放进 所有 颜色的篮子里（红、绿、黄都放）。
-
但是，它在每个篮子里的"分量"（权重
w_x）要变小 。变小的比例就是 "在那些颜色标签完整的水果里，这个颜色出现的比例" (tilde r_v)。 -
例子： 假设在颜色标签完整的水果里：
-
红色水果占 50% (
tilde r_红 = 0.5) -
绿色水果占 30% (
tilde r_绿 = 0.3) -
黄色水果占 20% (
tilde r_黄 = 0.2)
-
-
那么，一个颜色标签缺失的水果：
-
放进红篮子时，它在红篮子里的分量是
0.5 * 它原来的分量。 -
放进绿篮子时，它在绿篮子里的分量是
0.3 * 它原来的分量。 -
放进黄篮子时，它在黄篮子里的分量是
0.2 * 它原来的分量。
-
-
这样，这个缺失标签的水果相当于被"拆分"到了所有可能的篮子里，但在每个篮子里只占了一小部分（根据各颜色出现的可能性）。
-
-
简单总结分水果：好水果对号入座，分量不变；掉标签的水果所有位置都坐一点，分量按各位置原来的人数比例打折。
2.3神经网络
2.3.1神经元模型
神经网络的基本构成单元 ------ 神经元模型
-
神经元模型的生物学基础 神经网络试图模仿人脑的工作方式。人脑由数十亿个神经元（神经细胞）相互连接组成。每个神经元接收来自其他神经元的信号，当接收到的信号足够强时，它就会被"激活"，并向下一个神经元发送自己的信号。人工神经元模型就是对这一生物过程的数学抽象。
-
M-P 神经元模型 这是最基础的神经元模型，其工作原理为：
-
接收输入：
- 神经元接收来自其他
n个神经元（或输入源）的信号(x₁, x₂, ..., xₙ)。这些信号就像是它收到的"消息"。
- 神经元接收来自其他
-
加权求和：
-
每个输入信号
xᵢ都有一个与之关联的权重wᵢ。权重代表了该输入信号对这个神经元的重要性和影响力。-
正权重：表示兴奋性输入，会促使神经元激活。
-
负权重：表示抑制性输入，会阻止神经元激活。
-
权重绝对值大小：表示影响强度。
-
-
神经元将所有输入信号乘以各自的权重后求和 ，得到总输入值
z：
z = w₁*x₁ + w₂*x₂ + ... + wₙ*xₙ + b -
注意： 公式中通常包含一个偏置项
b(bias) 。你可以把它想象成神经元的"懒惰程度"或"激活难易程度"。它相当于一个固定的输入（通常x₀ = 1）的权重w₀，所以z = w₁*x₁ + ... + wₙ*xₙ + w₀*1。偏置b允许我们调整神经元激活的阈值点。
-
-
与阈值比较：
-
神经元有一个内置的阈值
θ。这个阈值代表激活所需的"最低兴奋度"。 -
计算机会将上一步得到的总输入值
z与这个阈值θ进行比较。
-
-
激活函数处理：
-
基于比较结果
(z - θ)或(z + b)，神经元需要通过一个激活函数f来决定它的输出y。 -
理想情况（阶跃函数）：
-
如果
(z - θ) >= 0(即总输入达到或超过阈值)，则输出y = 1(激活/兴奋)。 -
如果
(z - θ) < 0(即总输入低于阈值)，则输出y = 0(未激活/抑制)。 -
这个函数就像是一个开关，要么开(1)，要么关(0)。数学上称为阶跃函数 (Step Function)。
-
-
实际情况（常用 Sigmoid）：
-
阶跃函数虽然直观，但在数学上有一个大问题：它在
z - θ = 0这个点是不可导的（有个"跳跃"），而导数对于训练神经网络（通过梯度下降算法优化权重）至关重要。 -
因此，实践中常用Sigmoid 函数 作为激活函数。它的公式是：
σ(z) = 1 / (1 + e⁻ᶻ)（注：这里的
z通常已经包含了偏置b的效果，即z = w₁x₁ + ... + wₙxₙ + b，比较z和0等价于比较(z - θ)和0如果b = -θ）。 -
Sigmoid 函数的特性：
-
输出范围： 将任何实数输入
z挤压 到(0, 1)区间内。输出值无限接近于 0 或 1，但永远不会等于它们。 -
连续性 & 可导性： 它是光滑、连续的曲线，并且在所有点都有定义良好的导数。这点对于训练神经网络（使用梯度下降法更新权重）极其关键。
-
生物学解释： 可以理解为神经元的"激活程度"，0 代表完全不激活，1 代表完全激活，中间值代表不同程度的激活（兴奋）。这比阶跃函数的"非黑即白"更符合生物神经元的实际响应特性。
-
概率解释： 在二元分类问题中，Sigmoid 输出值可以自然地解释为样本属于正类（输出接近1）的概率。
-
-
-
-
产生输出：
-
最终，激活函数
f(无论是阶跃还是Sigmoid或其他) 的输出值y就是该神经元的输出信号。 -
这个输出信号
y会沿着连接（带有权重）传递给下游的其他神经元作为它们的输入。
-
-
-
激活函数 激活函数用于将神经元的输入转换为输出，关键作用是引入非线性：
- 理想激活函数：阶跃函数（如单位阶跃函数），能将输入映射为 "0"（抑制）或 "1"（兴奋），但存在不连续、不光滑的缺陷；
- 常用激活函数：Sigmoid 函数（如对数几率函数），可将输入挤压到 (0,1) 区间，具有连续可导的特性，更适合用于神经网络的参数学习。
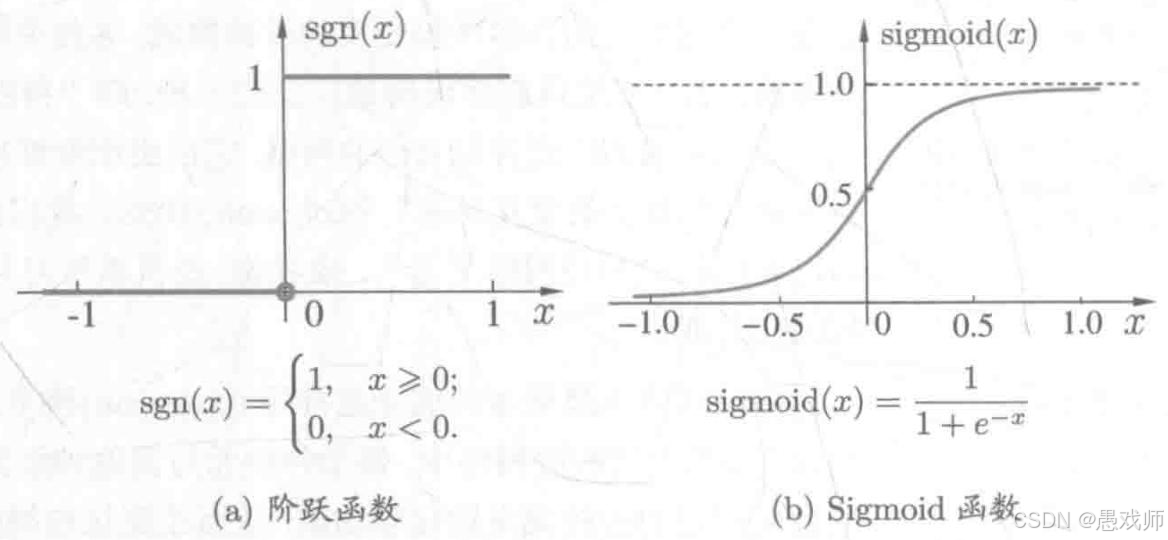
引用自西瓜书
激活函数是神经元模型的核心组件之一，它决定了神经元如何响应其总输入信号。它的作用不仅仅是简单的阈值判断：
-
引入非线性： 这是激活函数最重要的作用！如果神经元只做线性加权求和（z）而不经过非线性激活函数，那么无论堆叠多少层神经网络，整个网络的表达能力仍然等价于一个单层的线性模型（无法拟合复杂的非线性数据模式）。非线性激活函数（如Sigmoid）使得神经网络能够学习并表达极其复杂的函数关系，成为强大的"万能函数逼近器"。
-
控制输出范围： 如Sigmoid将输出限制在(0,1)，便于解释（如概率）或作为下一层神经元的输入（防止数值爆炸）。
-
决定神经元激活特性： 不同的激活函数有不同的"激活模式"（饱和性、梯度特性等），影响网络的学习动态和最终性能。
2.3.2感知机（Perceptron）及其扩展的多层网络
感知机模型
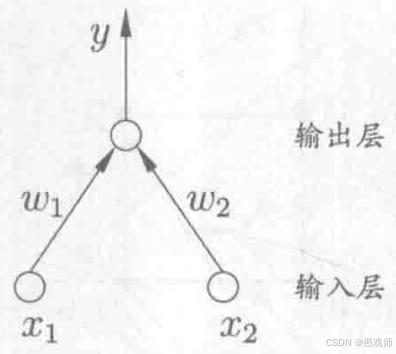
引用自西瓜书
把感知机想象成一个非常基础的人工"决策单元"。它接收一些输入（比如传感器信号或数据特征），根据简单的规则做出"是"或"否"（1 或 0）的判断
1. 结构：两层神经元
-
输入层：
-
由多个"神经元"组成，但这些神经元不是真正的计算单元。
-
它们的功能仅仅是接收 来自外界的输入信号
(x₁, x₂, ..., xₙ)以及一个固定输入为 1 的偏置项（对应阈值）。 -
接收到的信号原封不动地传递给下一层（输出层）的神经元。
-
-
输出层：
-
只有一个 真正的计算单元，它是一个 M-P 神经元。
-
这个神经元接收来自输入层的所有信号
(x₁, x₂, ..., xₙ, 1)。 -
它对每个输入信号乘以一个对应的权重
(w₁, w₂, ..., wₙ, w₀)（其中w₀是偏置b的权重，通常b = -θ）。 -
计算加权和 ：
z = w₁*x₁ + w₂*x₂ + ... + wₙ*xₙ + w₀*1（或等价于z = Σ wᵢxᵢ + b）。 -
将
z输入激活函数 。感知机使用的激活函数是阶跃函数 (Step Function)：-
如果
z >= 0，则输出y = 1。 -
如果
z < 0，则输出y = 0。
-
-
2. 功能：实现基本逻辑运算
感知机最核心的能力之一就是通过精心设置权重 (w₁, w₂, ..., wₙ, b) 来实现简单的逻辑门功能。这证明了它具有一定的计算能力。让我们用两个输入 (x₁, x₂) 的感知机来演示：
-
"与"运算 (AND) :
y = x₁ AND x₂(仅当x₁和x₂都为 1 时，y=1)-
权重设置：
w₁ = 1,w₂ = 1,b = -2(或者等效地θ = 2)。 -
计算验证：
-
(0, 0):z = 1*0 + 1*0 + (-2) = -2 < 0=>y=0 -
(0, 1):z = 1*0 + 1*1 + (-2) = -1 < 0=>y=0 -
(1, 0):z = 1*1 + 1*0 + (-2) = -1 < 0=>y=0 -
(1, 1):z = 1*1 + 1*1 + (-2) = 0 >= 0=>y=1
-
-
理解： 只有当两个输入信号都足够强（都为1），它们的加权和 (
1+1=2) 才能达到或超过阈值 (2)，从而激活神经元输出1。
-
-
"或"运算 (OR) :
y = x₁ OR x₂(只要x₁或x₂至少一个为 1，y=1)-
权重设置：
w₁ = 1,w₂ = 1,b = -0.5(或者等效地θ = 0.5)。 -
计算验证：
-
(0, 0):z = 1*0 + 1*0 + (-0.5) = -0.5 < 0=>y=0 -
(0, 1):z = 1*0 + 1*1 + (-0.5) = 0.5 >= 0=>y=1 -
(1, 0):z = 1*1 + 1*0 + (-0.5) = 0.5 >= 0=>y=1 -
(1, 1):z = 1*1 + 1*1 + (-0.5) = 1.5 >= 0=>y=1
-
-
理解： 只要有一个输入信号为1 (
w₁*1=1或w₂*1=1)，其值就超过了较低的阈值 (0.5)，足以激活神经元输出1。两个都为1时更强。
-
-
"非"运算 (NOT) :
y = NOT x₁(输出是输入的相反值)-
权重设置 (单输入)：
w₁ = -1.5,b = 1。 -
计算验证 (以
w₁ = -1.5,b = 1为例):-
x₁=0:z = (-1.5)*0 + 1 = 1 >= 0=>y=1(非0是1) -
x₁=1:z = (-1.5)*1 + 1 = -0.5 < 0=>y=0(非1是0)
-
-
理解： 负权重 (
w₁) 意味着输入信号会抑制神经元激活。当输入为0时，偏置b足够大，直接激活输出1。当输入为1时，负权重带来的抑制 (-1.5) 压倒了偏置 (+1)，导致总输入为负 (-0.5)，输出0。
-
3.学习规则：从错误中学习
感知机真正的力量在于它能自动学习正确的权重和偏置，而无需人工设定。它通过一个非常简单的规则，根据训练数据中的错误来调整自己。
-
目标： 对于给定的训练样本
(x, y)，其中x = (x₁, x₂, ..., xₙ)是输入特征，y是真实标签（通常是 0 或 1），感知机希望自己的预测输出ŷ尽可能接近y。 -
规则 (感知机学习规则)：
-
输入一个训练样本
(x, y)，计算感知机的预测输出ŷ。 -
比较预测
ŷ和真实值y：-
如果
ŷ = y：预测正确！ 什么都不做，权重和偏置保持不变。 -
如果
ŷ ≠ y：预测错误！ 需要调整权重和偏置。
-
-
权重/偏置更新公式：
-
wᵢ ← wᵢ + Δwᵢ -
Δwᵢ = η * (y - ŷ) * xᵢ -
等价公式：
wᵢ ← wᵢ + η * (y - ŷ) * xᵢ -
偏置更新 (同样规则)：
b ← b + η * (y - ŷ)(因为偏置b可以看作是对应输入恒为1的权重w₀，所以Δb = η * (y - ŷ) * 1)
-
-
关键参数：
-
η：学习率 (Learning Rate) 。这是一个大于0的小常数（例如0.1）。它控制着每次权重调整的步长。-
太小的
η：学习速度慢，需要更多次迭代才能收敛。 -
太大的
η：可能导致权重更新幅度过大，在最优解附近震荡甚至无法收敛。
-
-
(y - ŷ)：误差信号 (Error Signal) 。它只有3种可能值：-
ŷ=0, y=1(预测低了)：(1 - 0) = +1=> 增加 权重 (wᵢ向xᵢ的方向增加)。 -
ŷ=1, y=0(预测高了)：(0 - 1) = -1=> 减小 权重 (wᵢ向-xᵢ的方向增加)。 -
ŷ=y：(y - ŷ)=0=> 权重不变。
-
-
xᵢ：输入值。它决定了权重调整的方向和幅度。-
如果
xᵢ是大的正数，错误发生时权重wᵢ会获得较大的调整（增加或减少）。 -
如果
xᵢ是0或很小，它对权重wᵢ的调整影响就很小。 -
方向性： 公式
(y - ŷ) * xᵢ确保了权重调整的方向是朝着减少当前样本预测错误的方向。
-
-
-
学习过程示例 (学习"或"运算 OR)：
假设初始权重 w₁=0, w₂=0, b=0，学习率 η=0.5。
-
输入样本
(x₁=0, x₂=0), y=0:-
计算
z = 0*0 + 0*0 + 0 = 0,ŷ = step(0) = 1(预测错误!ŷ(1) ≠ y(0)) -
误差
(y - ŷ) = 0 - 1 = -1 -
更新权重:
-
Δw₁ = 0.5 * (-1) * 0 = 0=>w₁保持0 -
Δw₂ = 0.5 * (-1) * 0 = 0=>w₂保持0 -
Δb = 0.5 * (-1) * 1 = -0.5=>b = 0 + (-0.5) = -0.5
-
-
-
输入样本
(x₁=0, x₂=1), y=1:-
计算
z = 0*0 + 0*1 + (-0.5) = -0.5,ŷ = step(-0.5) = 0(预测错误!ŷ(0) ≠ y(1)) -
误差
(y - ŷ) = 1 - 0 = +1 -
更新权重:
-
Δw₁ = 0.5 * 1 * 0 = 0=>w₁保持0 -
Δw₂ = 0.5 * 1 * 1 = +0.5=>w₂ = 0 + 0.5 = 0.5 -
Δb = 0.5 * 1 * 1 = +0.5=>b = -0.5 + 0.5 = 0
-
-
-
输入样本
(x₁=1, x₂=0), y=1:- 计算
z = 0*1 + 0.5*0 + 0 = 0,ŷ = step(0) = 1(预测正确!) => 权重不变
- 计算
-
输入样本
(x₁=1, x₂=1), y=1:- 计算
z = 0*1 + 0.5*1 + 0 = 0.5,ŷ = 1(预测正确!) => 权重不变
- 计算
-
再次输入样本
(x₁=0, x₂=0), y=0:-
计算
z = 0*0 + 0.5*0 + 0 = 0,ŷ = step(0) = 1(预测错误!ŷ(1) ≠ y(0)) -
误差
(y - ŷ) = 0 - 1 = -1 -
更新权重:
-
Δw₁ = 0.5 * (-1) * 0 = 0=>w₁保持0 -
Δw₂ = 0.5 * (-1) * 0 = 0=>w₂保持0.5 -
Δb = 0.5 * (-1) * 1 = -0.5=>b = 0 + (-0.5) = -0.5
-
-
-
输入样本
(x₁=0, x₂=1), y=1:- 计算
z = 0*0 + 0.5*1 + (-0.5) = 0,ŷ = step(0) = 1(预测正确!) => 权重不变
- 计算
-
... 继续遍历样本，直到所有样本都被正确分类。
经过足够多的迭代（遍历所有样本多次），权重会收敛到类似 w₁≈1, w₂≈1, b≈-0.5 的值，成功学会"或"运算。
2.3.3. 感知机的局限与多层网络
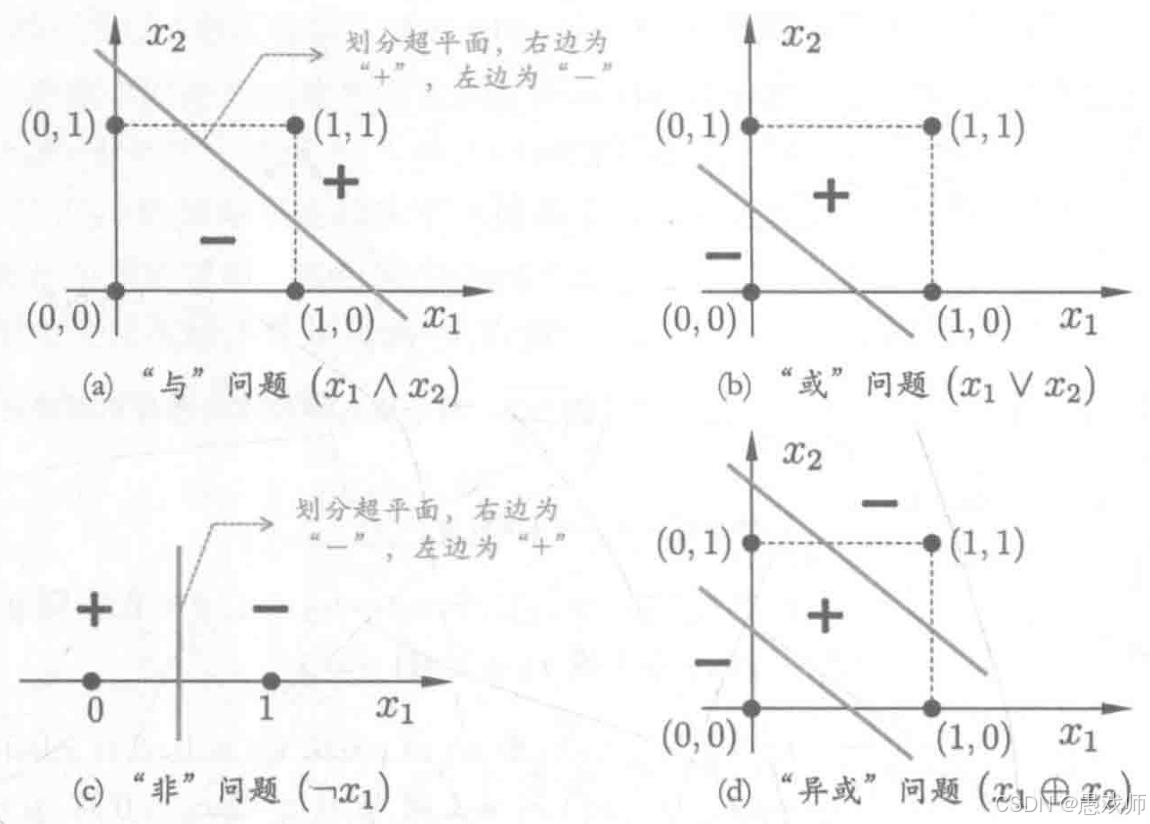引用自西瓜书
核心问题：感知机的局限 - 只能解决线性可分问题
-
什么是线性可分？
-
想象在二维平面上有两类点（比如红色点和蓝色点）。如果存在一条直线 ，能够把所有红色点划到直线的一侧，所有蓝色点划到直线的另一侧，那么这两类点就是线性可分的。
-
在高维空间（比如有 n 个特征），线性可分意味着存在一个 n-1 维的超平面（例如三维空间里的一个平面）可以完美地将不同类别的样本分开。
-
-
感知机的能力边界：
-
感知机（单层输出层，使用阶跃函数）本质上是一个线性分类器 。它的决策边界就是由加权和
z = Σ wᵢxᵢ + b = 0定义的一个超平面。 -
因此，感知机能够完美学习并分类任何线性可分的数据集。前面展示的"与"(AND)、"或"(OR)、"非"(NOT) 运算都是线性可分问题的典型例子（可以在二维平面上用一条直线分开）。
-
-
致命的局限：非线性可分问题 - 以"异或"(XOR)为例
-
"异或"运算 (XOR) 定义：当两个输入相异 （一个为 0，一个为 1）时，输出为 1；当两个输入相同（都为 0 或都为 1）时，输出为 0。
-
(0, 0) -> 0 -
(0, 1) -> 1 -
(1, 0) -> 1 -
(1, 1) -> 0
-
-
为什么感知机无法实现 XOR？（如上图所示）
-
尝试在二维平面上画出这 4 个点：
(0,0)和(1,1)是输出为 0 的点（假设用 ○ 表示），(0,1)和(1,0)是输出为 1 的点（假设用 × 表示）。 -
你会发现，没有任何一条直线能把所有的 ○ (0) 和所有的 × (1) 完美地分隔在直线的两侧！○ 在对角线上，× 在另一条对角线上。
-
数学证明（尝试设置权重）：
-
-
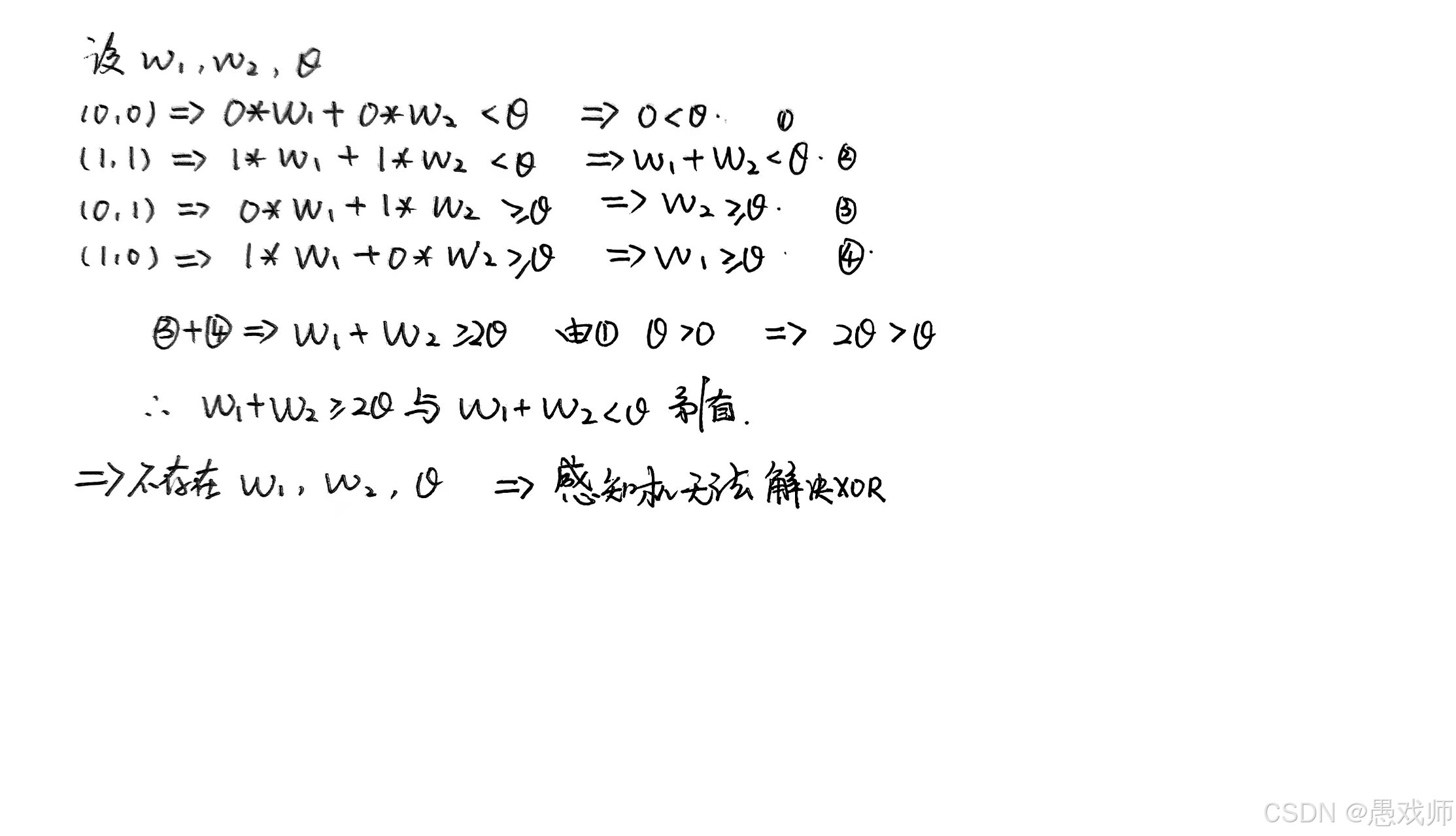
破局之道：多层网络（引入隐藏层）
既然一层功能神经元（感知机）能力有限，无法解决像 XOR 这样的非线性问题，很自然的想法就是：堆叠更多的层！
-
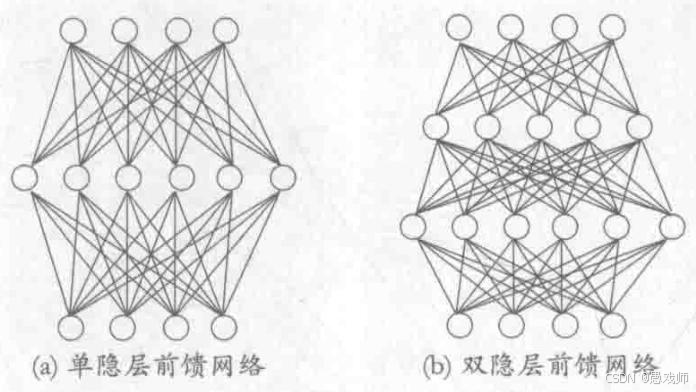
多层前馈网络 (Multi-Layer Feedforward Network):
-
结构：
-
输入层： 和感知机一样，仅接收输入。
-
隐藏层 (Hidden Layer)： 位于输入层和输出层之间的神经元层。这是关键！隐藏层中的神经元是真正的功能神经元（如 M-P 神经元）。一个网络可以有多个隐藏层。
-
输出层： 产生最终输出的功能神经元。
-
-
"前馈"： 信号从输入层单向流动，经过隐藏层，最终到达输出层。没有环或反馈。
-
激活函数： 隐藏层和输出层的神经元都需要激活函数。为了能够学习复杂的非线性关系，必须使用非线性激活函数（如 Sigmoid, ReLU）。如果使用线性激活函数，多层网络最终会等价于一个单层线性网络，失去意义。
-
-
为什么多层网络能解决非线性问题（以 XOR 为例）：
-
核心思想：特征变换。 隐藏层的作用是将原始输入空间映射到一个新的特征空间。在这个新空间中，原本线性不可分的问题可能变得线性可分。
-
用两层网络实现 XOR（1个隐藏层 + 1个输出层）：
假设隐藏层有两个神经元（H1, H2），输出层一个神经元（O）。使用阶跃函数激活。
-
H1 学习 "与" (AND-NOT)： 目标是当
x₁=1且x₂=0时激活。设置w₁₁=1, w₁₂=-1, θ₁=0.5(或b₁=-0.5)。-
(0,0): 1*0 + (-1)*0 = 0 < 0.5 -> 0 -
(0,1): 1*0 + (-1)*1 = -1 < 0.5 -> 0 -
(1,0): 1*1 + (-1)*0 = 1 >= 0.5 -> 1 -
(1,1): 1*1 + (-1)*1 = 0 < 0.5 -> 0
-
-
H2 学习 "或" (OR)： 目标是当
x₁=1或x₂=1时激活。设置w₂₁=1, w₂₂=1, θ₂=0.5(或b₂=-0.5)。-
(0,0): 0+0=0 < 0.5 -> 0 -
(0,1): 0+1=1 >= 0.5 -> 1 -
(1,0): 1+0=1 >= 0.5 -> 1 -
(1,1): 1+1=2 >= 0.5 -> 1
-
-
输出层 O 学习 "与" (AND)： 目标是当 H1 和 H2 的输出不同 （即一个是 1，一个是 0）时输出 1。注意 H1 和 H2 的输出
(h₁, h₂)：-
(0,0) -> (0,0) -> O 希望输出 0 -
(0,1) -> (0,1) -> O 希望输出 1(异) -
(1,0) -> (1,0) -> O 希望输出 1(异) -
(1,1) -> (0,1)但根据 H1 计算(1,1)->0，H2 计算(1,1)->1，所以是(0,1) -> O 希望输出 1? 等等，不对！ -
仔细看 H1 在
(1,1)输出是0，H2 在(1,1)输出是1，所以组合(h₁, h₂) = (0,1)。而(0,1)在输入层对应(0,1)和(1,1)两个样本。我们需要 O 在(0,1)输出 1 (对应原始输入(0,1))，在(0,1)(也对应原始输入(1,1)) 输出 0。矛盾！
-
-
调整（更通用的方法）： 让 H1 学习
NAND(与非：NOT (x₁ AND x₂))，即(1,1)输出 0，其他输出 1。设置w₁₁=-1, w₁₂=-1, θ₁=-1.5(或b₁=1.5)。-
(0,0): -0-0=0 >= -1.5?(阶跃z>=0)0>=0?假设θ是阈值比较z>=θ，则0 >= -1.5 -> 1(正确) -
(0,1): -0-1=-1 >= -1.5?-1 >= -1.5 -> 1(正确) -
(1,0): -1-0=-1 >= -1.5 -> 1(正确) -
(1,1): -1-1=-2 >= -1.5?-2 >= -1.5?No -> 0(正确)
-
-
让 H2 学习
OR(或)，如前所述w₂₁=1, w₂₂=1, θ₂=0.5。 -
现在隐藏层输出
(h₁, h₂)：-
(0,0) -> (NAND=1, OR=0) -> (1,0) -
(0,1) -> (NAND=1, OR=1) -> (1,1) -
(1,0) -> (NAND=1, OR=1) -> (1,1) -
(1,1) -> (NAND=0, OR=1) -> (0,1)
-
-
输出层 O 学习 "与非"(NAND) 或 "或非"(NOR)？ 观察目标输出 y：
-
当
(h₁, h₂) = (1,0)(对应(0,0)) ->y=0 -
当
(h₁, h₂) = (1,1)(对应(0,1)和(1,0)) ->y=1 -
当
(h₁, h₂) = (0,1)(对应(1,1)) ->y=0
-
-
这实际上是在
(h₁, h₂)空间上，对点(1,0),(0,1)(y=0) 和(1,1)(y=1) 进行分类。这是线性可分的！ 例如，可以学习一个简单的AND：-
设置
w_o1=1, w_o2=1, θ_o=1.5(或b_o=-1.5)。 -
(1,0): 1*1 + 1*0 = 1 < 1.5?(阶跃z>=θ)1>=1.5?No -> 0(正确) -
(1,1): 1*1 + 1*1 = 2 >= 1.5 -> 1(正确) -
(0,1): 1*0 + 1*1 = 1 < 1.5 -> 0(正确)
-
-
-
关键理解：
-
输入层
(x₁, x₂)是线性不可分的（无法用一条直线分开 ○ 和 ×）。 -
隐藏层 H1 (NAND) 和 H2 (OR) 将原始输入空间
(x₁, x₂)变换到了新的特征空间(h₁, h₂)。 -
在这个新的
(h₁, h₂)特征空间中，代表不同原始类别的点(1,0),(1,1),(0,1)变得线性可分 了（可以用一条直线，比如h₁ + h₂ >= 1.5来区分y=1和y=0）。 -
输出层 O (AND) 在这个新空间上做了一个简单的线性分类。
-
-
-
多层网络的威力和必要性：
-
解决非线性问题： 通过引入一个或多个隐藏层和非线性激活函数，多层网络能够学习极其复杂的非线性决策边界，解决感知机无能为力的非线性可分问题（如 XOR、复杂的图像分类、自然语言处理等）。
-
特征学习： 隐藏层自动地从原始输入数据中学习并提取层级化的特征表示 (Hierarchical Feature Representation)。
-
底层隐藏层可能学习到简单的局部特征（如边缘、颜色斑点）。
-
高层隐藏层可能将这些简单特征组合成更复杂的、全局的特征（如物体部件、整个物体）。
-
-
通用近似定理 (Universal Approximation Theorem)： 一个关键的理论基础指出，只需一个包含足够多神经元的隐藏层的前馈神经网络 ，就能够以任意精度逼近定义在实数空间中的任意复杂度的连续函数。这从理论上证明了多层网络强大的表达能力。
-
超越感知机： 多层感知机 (MLP - Multi-Layer Perceptron)，即具有至少一个隐藏层并使用非线性激活函数（如 Sigmoid, ReLU）的前馈网络，成为了构建更复杂、更强大的神经网络模型（如卷积神经网络 CNN、循环神经网络 RNN）的基础构件。
-
2.3.4多层前馈神经网络
核心概念：超越感知机的"智能"加工厂
想象一个更复杂的工厂（相比感知机那个小作坊）：
-
原材料入口： 输入层接收原始数据（如图像像素、单词编码、传感器读数）。
-
多级加工车间： 隐藏层（可以有多层）对原材料进行多步骤、越来越精细的加工。每个车间（神经元）都有自己独特的加工工具（权重）和质检标准（阈值/偏置）。
-
成品输出： 输出层将最终加工结果包装成需要的格式（如分类标签、预测数值）。
-
流水线规则： 材料只能从入口（输入层）按顺序流经各个车间（隐藏层），最后到达出口（输出层），不能倒流或跨车间跳跃。
层级化与连接性
-
输入层 (Input Layer):
-
角色： 纯粹的"接收站"。不进行任何计算。
-
神经元： 每个神经元代表输入数据的一个特征（例如，一张28x28灰度图片有784个输入神经元，每个对应一个像素的亮度值）。
-
输出： 直接将接收到的输入值
x₁, x₂, ..., xₙ原封不动地传递给下一层（第一个隐藏层）的每一个神经元。
-
-
隐藏层 (Hidden Layer(s)):
-
角色： 网络的"大脑"和"引擎"。负责从输入数据中学习、提取和组合特征。是网络具备强大非线性能力的关键。
-
神经元： 功能神经元 。每个隐藏神经元都是一个 M-P神经元 的增强版：
-
接收输入： 接收来自前一层所有神经元的输出（对于第一个隐藏层，就是输入层的输入值）。
-
加权求和： 计算加权和
z⁽ˡ⁾_j = Σᵢ (w⁽ˡ⁾_{ji} * a⁽ˡ⁻¹⁾_i) + b⁽ˡ⁾_j-
l 表示层索引（例如
l=1表示第一个隐藏层） -
j表示当前层第j个神经元 -
i表示前一层（l-1层）的神经元索引 -
w⁽ˡ⁾_{ji}：连接前一层神经元i到当前层神经元j的权重。 -
a⁽ˡ⁻¹⁾_i：前一层神经元i的输出值（即激活值）。 -
b⁽ˡ⁾_j：当前层神经元j的偏置项。
-
-
激活函数： 将加权和
z⁽ˡ⁾_j输入到一个非线性激活函数g(·)中，得到该神经元的输出（激活值）a⁽ˡ⁾_j = g(z⁽ˡ⁾_j)。- 为什么必须是非线性？ 如果使用线性函数，无论堆叠多少层，整个网络的最终输出仍然是输入的线性组合，失去解决复杂非线性问题的能力。常用非线性激活函数包括 Sigmoid, Tanh, ReLU (Rectified Linear Unit) 等。
-
-
层数 & 神经元数量： 网络可以包含一个或多个 隐藏层。每层可以包含任意数量 的神经元。层数和每层神经元数是网络的超参数，需要根据任务和数据调整。
-
"隐藏"含义： 这些层在训练数据和最终输出之间，其值不直接可见于输入或输出，故称"隐藏"。
-
-
输出层 (Output Layer):
-
角色： 产生网络的最终预测结果。
-
神经元： 功能神经元。结构与隐藏层神经元类似：
-
接收来自最后一个隐藏层所有神经元的输出。
-
计算加权和
z⁽ᴸ⁾_k = Σⱼ (w⁽ᴸ⁾_{kj} * a⁽ᴸ⁻¹⁾_j) + b⁽ᴸ⁾_k(L表示输出层)。 -
通过激活函数
σ(·)得到最终输出yₖ = σ(z⁽ᴸ⁾_k)或ŷₖ = σ(z⁽ᴸ⁾_k)。
-
-
激活函数选择： 取决于任务类型：
-
回归任务 (预测连续值)： 通常使用线性激活函数 （
σ(z) = z）或 ReLU。 -
二分类任务： 通常使用 Sigmoid 函数 ，将输出压缩到
(0,1)区间，解释为属于正类的概率。 -
多分类任务： 通常使用 Softmax 函数，将输出转化为概率分布（所有输出神经元之和为1）。
-
-
-
连接方式：全连接 (Fully Connected / Dense):
-
定义： 本层的每一个神经元 都与下一层的每一个神经元相连接。
-
图示： 想象每一层的神经元排成一排，相邻两层的神经元之间，所有可能的连接线都存在，形成一个完全二分图,如下图所示。
-
关键约束：
-
无同层连接： 同一层内的神经元之间没有连接。它们彼此独立计算，仅通过下一层进行交互。
-
无跨层连接： 信号只能逐层传递，不能跳过中间层（如输入层不能直接连到输出层）。
-
无反馈/循环： 信号单向流动，从输入层 -> 隐藏层1 -> 隐藏层2 -> ... -> 输出层。没有信号从后层流回前层（这是与前馈循环网络 RNN 的关键区别）。
引用自西瓜书
2.3.5误差逆传播（BP）算法
BP算法就是让多层神经网络通过前向传播 做预测、计算误差 ，然后利用梯度下降 和链式法则 进行误差反向传播 ，一层层计算出每个参数（权重/阈值）该负多少责任（梯度），再用这个责任和学习率去更新参数 ，不断迭代让预测越来越准。为了防止学成"书呆子"（过拟合），要用早停 或正则化 来提升泛化能力。本质是：试错 -> 追责 -> 改进 -> 再试错。
引用自西瓜书
核心目标：
通过迭代调整网络中的所有权重（w）和偏置（b），使网络对于训练样本的预测输出 ŷ 尽可能接近真实目标 y，从而最小化一个预先定义的损失函数 L。
基本原理：梯度下降与误差反向传播
BP 算法是梯度下降（Gradient Descent）算法在神经网络这一特定、复杂结构上的高效实现。其核心思想可以概括为：
-
前向传播 (Forward Pass)： 输入一个训练样本
x，数据从输入层流向输出层。网络根据当前的权重w和偏置b逐层计算每个神经元的加权输入z和激活输出a，最终得到预测输出ŷ。 -
计算误差 (Loss Calculation)： 比较预测输出
ŷ和真实目标y，计算损失函数L(ŷ, y)的值。损失函数量化了网络当前预测的"错误程度"（例如，均方误差 MSE 或交叉熵损失 Cross-Entropy）。 -
反向传播 (Backward Pass)： 这是 BP 算法的精髓所在。 目标是计算损失函数
L相对于网络中每一个可学习参数（每一个w和 每一个b）的梯度∂L/∂w和∂L/∂b。-
为什么叫"反向"？ 计算梯度的过程从输出层开始 ，利用链式法则 ，沿着与信息前向传播相反的方向 （从输出层 -> 最后一个隐藏层 -> ... -> 第一个隐藏层 -> 输入层），将"误差信号"或"责任"一层一层地反向传播回去。
-
关键概念：误差项
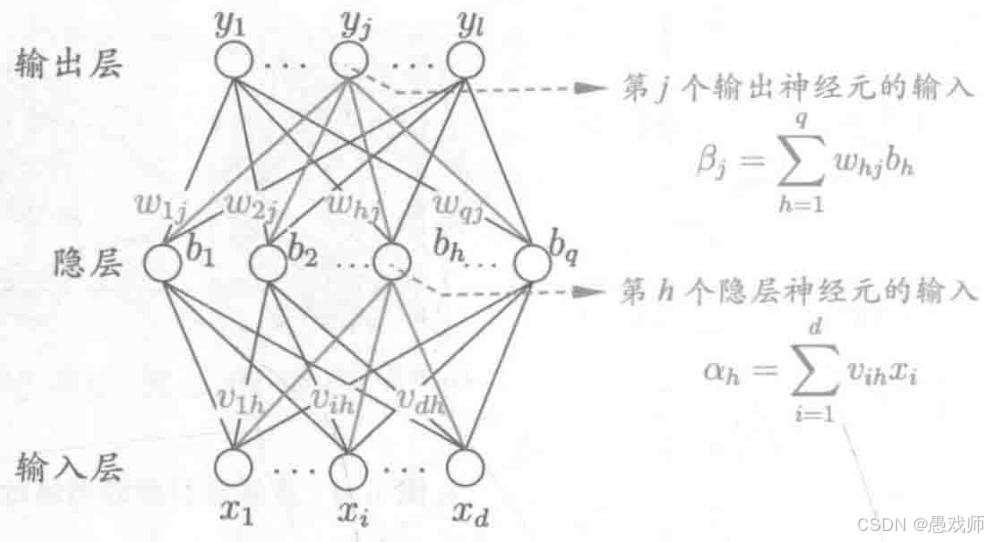
δ： 为了高效计算梯度，BP 算法定义了一个非常重要的中间量：第l层第j个神经元的误差项δⱼ⁽ˡ⁾。它被定义为损失函数L相对于该神经元加权输入zⱼ⁽ˡ⁾的偏导数：
δⱼ⁽ˡ⁾ = ∂L / ∂zⱼ⁽ˡ⁾这个误差项
δⱼ⁽ˡ⁾直观地表示了：该神经元的加权输入zⱼ⁽ˡ⁾发生微小变化时，对最终损失L的影响大小和方向。它是反向传播过程中传递的核心信息。
-
-
参数更新 (Parameter Update)： 利用在第 3 步中计算出的所有梯度
(∂L/∂w, ∂L/∂b)，按照梯度下降的原则更新网络参数：-
w⁽ˡ⁾_{ji} ← w⁽ˡ⁾_{ji} - η * (∂L / ∂w⁽ˡ⁾_{ji}) -
bⱼ⁽ˡ⁾ ← bⱼ⁽ˡ⁾ - η * (∂L / ∂bⱼ⁽ˡ⁾)其中
η是学习率 (Learning Rate) ，一个控制参数更新步长大小的超参数。负号表示沿着梯度的反方向 （即损失函数下降最快的方向）更新参数，目的是减小损失L。
-
用一个比方来解释：
基本原理：学做菜的厨房
-
适用场景： 你想训练一个有很多层"厨师"（神经元）的厨房（神经网络），让它学会做一道复杂的菜（比如：预测房价、识别人脸）。厨房结构是固定的（输入层->隐藏层->输出层），但每个厨师放调料的习惯（连接权）和火候偏好（阈值）一开始都是瞎蒙的。
-
核心思想： 试错 + 改进。
-
前向传播 (做菜)： 你把食材（输入数据）交给第一个厨师（输入层）。他简单处理一下传给下一层的几个"资深厨师"（隐藏层）。资深厨师们根据自己的调料习惯（权重）和火候偏好（阈值）加工食材，然后把半成品传给最后的大厨（输出层）。大厨综合所有半成品，加入自己的调料和火候，端出最终菜品（预测结果）。
-
尝味道 (算误差)： 你尝一口（对比预测结果
ŷ和真实结果y），皱眉头说："太咸了！离标准味道差得远！" 这个"差得远"的程度就是误差 (E)。 -
反向传播 (找责任)： 现在关键来了！菜做砸了，谁的责任？是大厨盐放多了？还是某个资深厨师提供的酱料本身就太咸？或者是食材处理阶段就出了问题？BP算法就像一个精明的监工：
-
他先批评大厨（输出层）："你的菜太咸了（误差大），扣你工资（更新权重/阈值）！扣多少？根据你多放了多少盐（误差的梯度）来定！"
-
接着，大厨说："我的咸是因为张资深厨师（隐藏层某个神经元）给我的酱料本身就咸！" 监工就去找张厨师："大厨说你的酱料太咸导致了他的问题（误差反向传播到隐藏层），你也要负责！扣你工资（更新权重/阈值）！扣多少？根据你的酱料对大厨的咸度有多大影响（链式法则计算梯度）来定！"
-
张厨师可能还会甩锅给处理食材的小工... 就这样一层层反向追责下去，直到最开始的食材处理环节（输入层）。
-
-
更新参数 (改进)： 监工根据追责结果（计算出的梯度），告诉每个厨师："你下次做这道菜时，盐少放一点 （调整权重），火候调小一点 （调整阈值）。" 调整的幅度由一个叫"学习率 (
η)"的老板决定，老板怕厨师改得太猛（学习率太大）或者太保守（学习率太小）。
-
简单总结： 前向传播是做菜，反向传播是根据菜的味道（误差）一层层追责，找到每个厨师（神经元）该背多少锅（梯度），然后让他们下次做菜时调整调料和火候（更新权重和阈值），目标是让菜越做越好吃（误差越来越小）。
网络结构与变量：厨房的架构和工具
-
结构：
-
输入层： 处理原始食材的人（比如洗菜工、切菜工）。人数 (
d) 由食材种类决定（比如客户资料有年龄、收入、职业等d项）。 -
隐藏层： 真正的烹饪主力（资深厨师）。厨房可以有多层，这里假设一层 (
q个厨师)。他们负责把初步处理的食材加工成复杂的半成品（特征提取）。 -
输出层： 最终摆盘的大厨 (
l个)。人数由要预测的结果决定（比如预测"违约/不违约"就是1个厨师；预测"猫/狗/兔子"就是3个厨师）。
-
-
关键变量 (厨师的习惯)：
-
权重 (
v_ih,w_hj)： 厨师们"放调料的比例"。比如v_ih是洗菜工i传给资深厨师h的菜量对h最终调味的影响权重。w_hj是资深厨师h的半成品对大厨j最终调味的影响权重。 -
阈值 (
γ_h,θ_j)： 厨师们的"火候偏好"或"敏感度"。阈值越高，这个厨师越"迟钝"，需要更强烈的输入（更浓的味道）才能被激活（做出反应）。 -
激活函数 (
f，常用 Sigmoid)： 每个厨师自己独特的"调味方式"。Sigmoid 函数就像一个"压汁器"，不管输入多大（多浓的汤汁），它都给你压成一个 0 到 1 之间的值（比如 0.2 代表微辣，0.8 代表特辣）。它有个超棒的特性 ：厨师调整调料（输入）对最终味道（输出）的改变率（导数f'）很容易算出来（f' = f(1-f)），这对监工计算责任（梯度）非常方便！ -
输出 (
b_h,ŷ_j)： 资深厨师h做好的半成品味道 (b_h)，大厨j最终端上桌的菜的味道 (ŷ_j)。
-
误差计算与参数更新：监工的算盘
-
误差 (
E_k)： 监工尝菜后，计算实际味道 (y_j^k) 和 大厨做的味道 (ŷ_j^k) 差了多少。用的是均方误差：把每种味道的差的平方加起来再除以2（方便计算导数）。差得越多，误差越大，监工越生气。 -
参数更新规则 (扣工资/改进方案)：
-
输出层 (大厨
j的责任)：-
责任 (
g_j)：g_j = (大厨的菜味道 ŷ_j) * (1 - ŷ_j) * (真实味道 y_j - ŷ_j)。这考虑了：1) 大厨当前味道的"可调性"（Sigmoid 特性ŷ(1-ŷ)）；2) 味道差多少 (y_j - ŷ_j)。差越大，责任越大。 -
调整调料 (
Δw_hj)： 大厨j调整他从资深厨师h那里拿的半成品 (b_h) 的重视程度。Δw_hj = η * g_j * b_h。责任 (g_j) 越大、资深厨师h的半成品 (b_h) 味道越重，调整幅度越大。学习率 (η) 控制整体调整力度。 -
调整火候 (
Δθ_j)：Δθ_j = -η * g_j。责任 (g_j) 越大，火候偏好（阈值）调整幅度越大（负号表示往减少误差的方向调）。
-
-
隐藏层 (资深厨师
h的责任)：-
责任 (
e_h)：e_h = (资深厨师的半成品味道 b_h) * (1 - b_h) * (他影响的所有大厨的责任之和 ∑ w_hj * g_j)。这考虑了：1) 资深厨师自己半成品的"可调性" (b_h(1-b_h)）；2) 他影响的所有 大厨的责任 (g_j) 有多大，以及他对那些大厨的影响权重 (w_hj) 有多强。他影响的大厨们责任越大、他影响越大，他的责任也越大。 -
调整调料 (
Δv_ih)： 资深厨师h调整他从洗菜工i那里拿的原始食材 (x_i) 的重视程度。Δv_ih = η * e_h * x_i。他的责任 (e_h) 越大、原始食材 (x_i) 分量越足，调整幅度越大。 -
调整火候 (
Δγ_h)：Δγ_h = -η * e_h。责任 (e_h) 越大，火候偏好（阈值）调整幅度越大。
-
-
简单总结： 监工先算大厨的责任有多重（g_j），扣他工资（更新 w_hj, θ_j）。大厨甩锅："是张资深厨师 (h) 的酱料害的！"。监工就去算张厨师的责任 (e_h)，这责任取决于：1) 张厨师自己的问题 (b_h(1-b_h)）；2) 被他坑的大厨们 (g_j) 的问题有多严重以及他对大厨们 (w_hj) 的影响有多大。然后扣张厨师的工资（更新 v_ih, γ_h）。
数学推导
2.3.6 神经网络训练中的 "参数寻优" 问题
"全局最小" 与 "局部极小" 的概念及相关优化策略
1. 基本概念
- 误差函数 ：神经网络在训练集上的误差E是关于连接权w和阈值
- 局部极小 ：若存在参数
- 全局最小 ：若参数空间中所有参数的误差均不小于
2. 梯度下降法的局限
基于梯度的搜索（如 BP 算法使用的梯度下降）是常用参数寻优方法，其沿负梯度方向更新参数。但当误差函数存在多个局部极小时，算法可能陷入局部极小（此时梯度为零，参数更新停止），无法找到全局最小。
3. 跳出局部极小的策略
实际任务中，常用启发式策略尝试接近全局最小：
- 多初始点：用多组不同初始参数训练多个网络，选择误差最小的结果（增加找到全局最小附近参数的概率）。
- 模拟退火：每步以一定概率接受 "次优解"（误差更大的解），概率随时间降低，既可能跳出局部极小，又保证最终收敛。
- 随机梯度下降：计算梯度时引入随机因素，即使陷入局部极小，梯度仍可能非零，有机会继续搜索。
- 遗传算法：通过模拟生物进化的选择、交叉、变异机制优化参数，有助于跳出局部极小。
核心逻辑
神经网络训练的参数寻优易受局部极小影响，需通过多种策略缓解；这些策略虽缺乏严格理论保障，但在实践中能有效提升找到全局最小附近参数的概率，改善网络泛化性能。