递归的运用---实现排列型，组合型，指数型枚举的过程

今天下午主要是看了一下这个递归是如何实现枚举的，分别是对应的不同的枚举的方式，指数型枚举，组合型枚举；

1.第一题

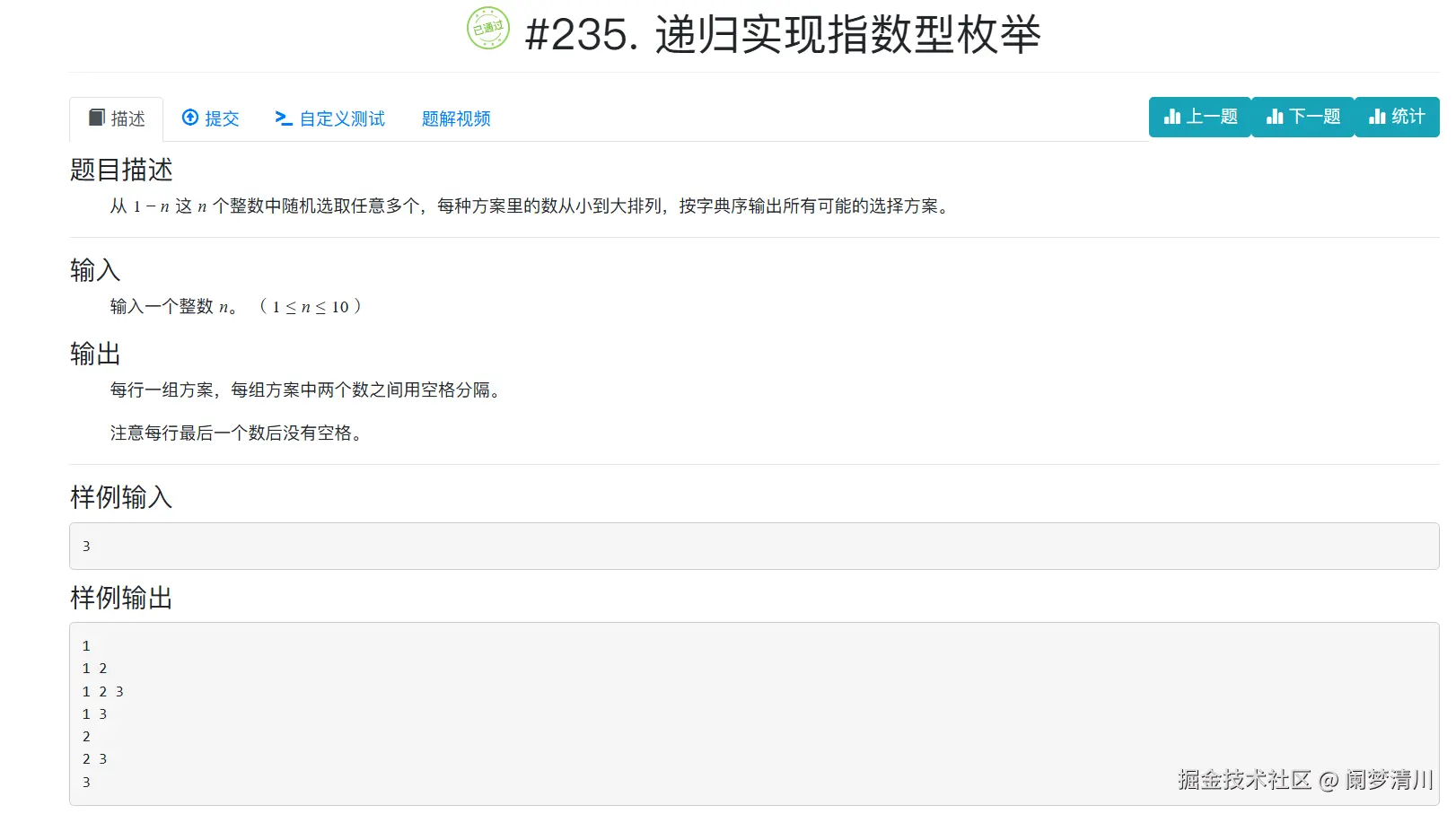
下面的这个是代码：

1）接下来的三个题目代码基本上都是下面的这个结构，funx函数负责的就是我们的这个递归的过程

2）上面的这个图片里面的案例其实就已经说明了很多问题，就是这个输入输出的内容和规律我们肯定可以明白这个枚举的过程的；

3）cnt控制的事我们输出的内容的数据个数，里面有一个for循环是对于这个空格进行输出的控制的；

4）func(i+1)就是从后面的一个数据开始继续进行这个递归的过程，例如，之前的数据是1开头的，这个时候我们就需要从2开始这个递归的过程；

5）cnt--就是我们每一次进行这个回溯的过程，也就是回到之前的状态，再次做出选择；

ini 复制代码

#include<iostream>
using namespace std;
int num[15],cnt,n;
void func(int s)
    {
    for(int i=s;i<=n;i++)
    {
        num[cnt]=i;
        cnt++;
        for(int j=0;j<cnt;j++)
            {
            if (j != 0) cout << " ";
            cout<<num[j];
        }
        cout<<endl;
        func(i+1);
        cnt--;
    }
}
int main()
    {
    cin>>n;
    func(1);
    return 0;
}

2.第二题

下面的这个算是组合型枚举，输入的数据的参数是确定的，输入的参数是两个，输出的数据的个数也是确定的，不像上面的那个样子输出的里面的个数有波动；

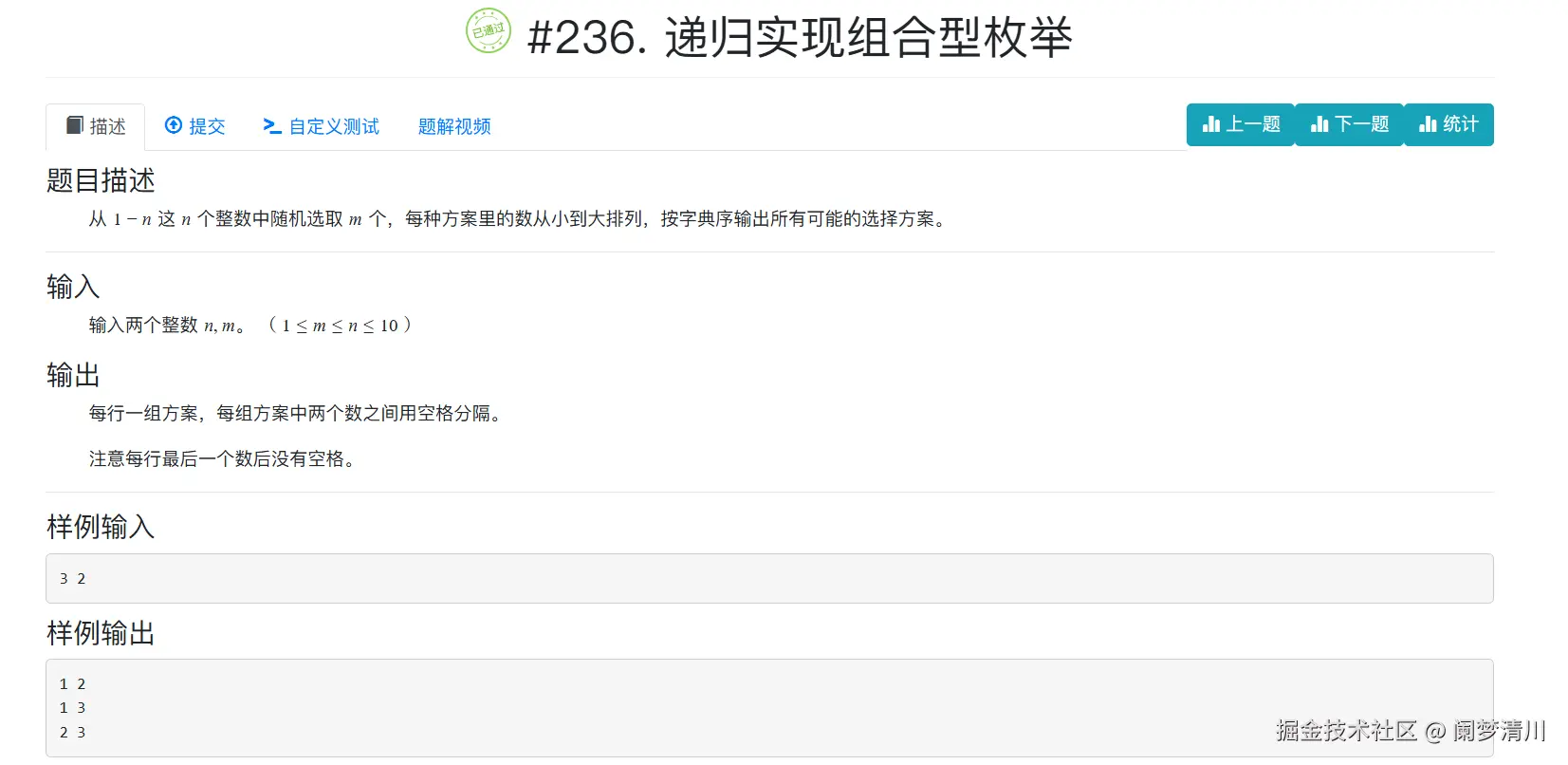
下面的这个是我们的代码：

1）func调用的时候第一个参数是1表示从几开始，m表示的就是剩下的需要进行选择的这个数据的个数；

2）left==0表示的就是我们的这个递归的结束的条件，直接进行这个输出即可，cnt控制的就是我们的输出里面的个数，这个进行是否为0判断主要是为了解决这个输出里面的空格的问题；

3）第二个for循环表示的就是我们的递归的过程，func(i+1)表示的就是接着递归，left-1表示的这个新一轮剩下的这个数据的个数，cnt--就是进行回溯的过程；

ini 复制代码

#include<iostream>
using namespace std;
int n, m, num[15], cnt;
void func(int s, int left)
{
    if (left == 0) {
        for (int i = 0; i <cnt; i++)
        {
            if (i != 0)
            {
                cout << " ";
            }
            cout << num[i];
        }
        cout << endl;
        return;
    }
    for (int i = s; i <= n - left + 1; i++)
    {
        num[cnt] = i;
        cnt++;
        func(i + 1, left - 1);
        cnt--;
    }
}
int main()
{
    cin >> n >> m;
    func(1, m);
    return 0;
}

3.第三题

下面的这个是题目：排列行枚举主要强调的就是这个排列的过程，因此这个选过的数据就不可以再次出现了；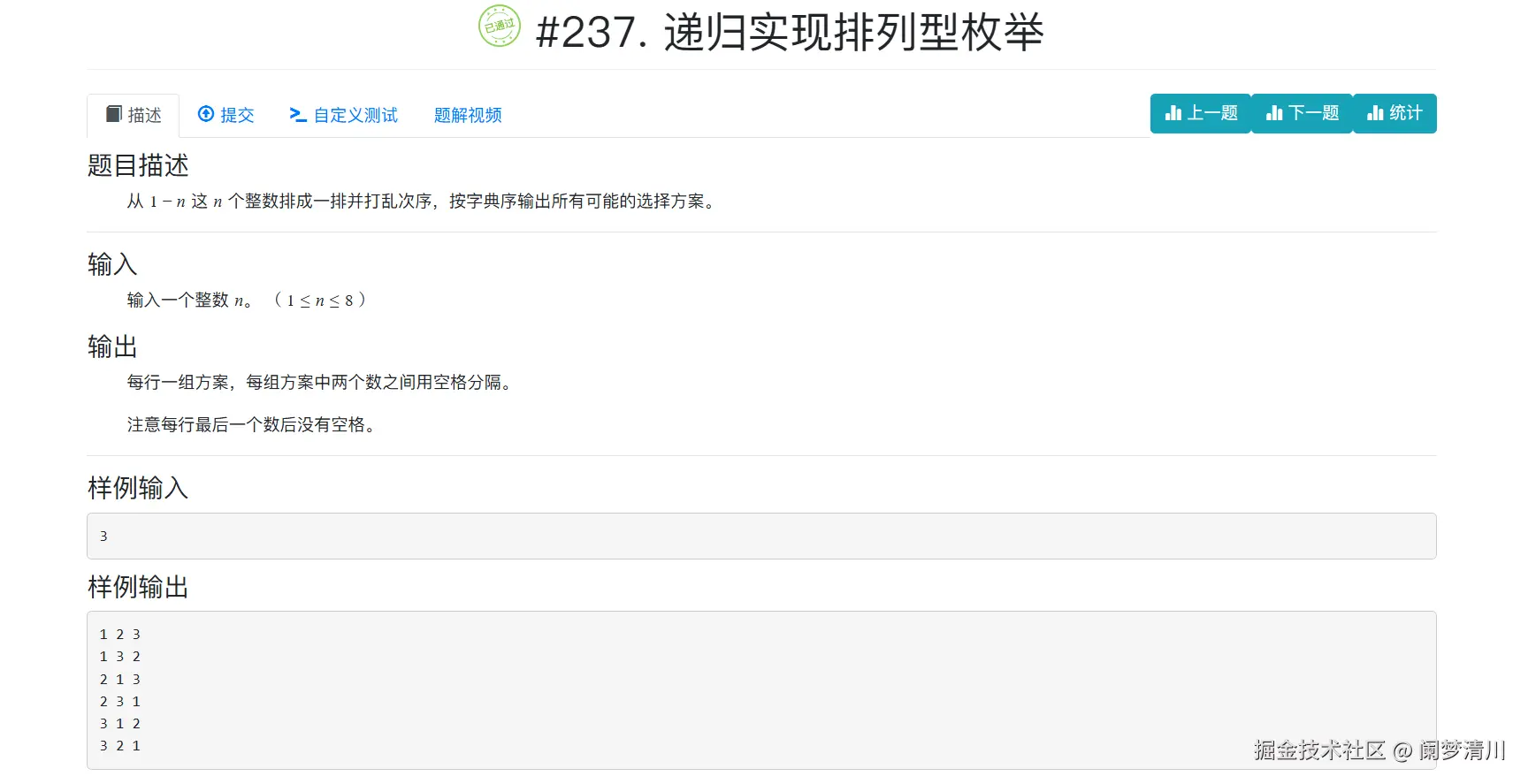

下面的这个事代码：

1）func还是实现我们的这个逻辑的函数，left==0还是进行这个递归结束的条件的判断说明；

2）mark数组主要就是标记我们的这个数据有没有被选中过，有没有被使用过，0表示的就是没有被使用过，这个时候我们就需要放到这个数组里面去，然后赋值为1，表示这个数据已经被使用了，后面不可以再被选中

3）func(left-1)表示的就是这个时候需要选择的个数减少了一个，接下来就是回溯，也就是回到开始的状态，这个时候就是cnt--，回溯的时候，我们之前使用数据是可以被再次使用的，也就是相当于开始新的一轮，因此这个时候我们的mark,这个表示数据有没有被使用的数组，也是需要置为0，表示处于原始没有被使用的状态，开始新一轮的选择；

ini 复制代码

#include<iostream>
using namespace std;
int n, num[15], mark[15], cnt;
void func(int left)
{
    if (left == 0)
    {
        for (int i = 0; i < cnt; i++)
        {
            if (i != 0) {
                cout << " ";
            }
            cout << num[i];
        }
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++)
    {
        if (mark[i] == 0)
        {
            mark[i] = 1;
            num[cnt] = i;
            cnt++;
            func(left - 1);
            cnt--;
            mark[i] = 0;
        }
    }
}
int main()
{
    cin >> n;
    func(n);
    return 0;
}