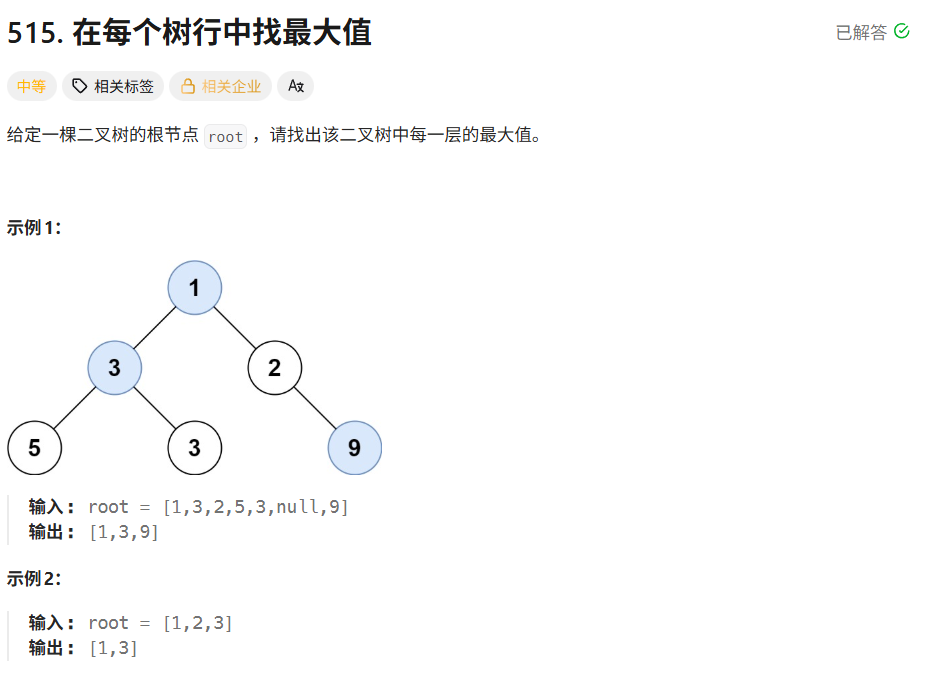
算法思路说明:
-
BFS层序遍历:使用队列进行广度优先搜索,按层遍历二叉树
-
每层最大值计算:
-
初始化每层的最大值为
INT_MIN(最小整数,包含在<climits>或<limits.h>中) -
遍历每层所有节点,不断更新最大值
-
-
更新最大值的技巧
cpp
// 方法1:使用条件运算符
maxValue = node->val > maxValue ? node->val : maxValue;
// 方法2:使用max函数
maxValue = max(maxValue, node->val);-
INT_MIN:
-
是C/C++中的宏定义,表示最小整数值(通常是-2147483648)
-
需要包含头文件
<climits>或<limits.h> -
如果不包含头文件,在一些编译器中使用INT_MIN可能会报错
-
cpp
class Solution {
public:
// 找出二叉树每一层中的最大值
vector<int> largestValues(TreeNode* root) {
// 创建队列用于BFS层序遍历
queue<TreeNode*> que;
// 如果根节点不为空,将其加入队列
if (root != NULL) que.push(root);
// 存储结果的向量,将保存每一层的最大值
vector<int> result;
// 当队列不为空时,继续遍历
while (!que.empty()) {
// 获取当前层的节点数量
int size = que.size();
// 初始化当前层的最大值
// 使用INT_MIN(最小整数值)作为初始值,确保任何节点值都会比它大
int maxValue = INT_MIN;
// 遍历当前层的所有节点
for (int i = 0; i < size; i++) {
// 取出队首节点
TreeNode* node = que.front();
que.pop();
// 更新当前层的最大值
// 如果当前节点值大于maxValue,则更新maxValue
// 这是条件运算符:condition ? expr1 : expr2
// 当node->val > maxValue为真时,返回node->val,否则返回maxValue
maxValue = node->val > maxValue ? node->val : maxValue;
// 将当前节点的左子节点加入队列(如果存在)
if (node->left) que.push(node->left);
// 将当前节点的右子节点加入队列(如果存在)
if (node->right) que.push(node->right);
}
// 将当前层的最大值加入结果数组
result.push_back(maxValue);
}
// 返回每层最大值的向量
return result;
}
};带头文件的完整代码,包含了输入输出
cpp
#include <iostream>
#include <vector>
#include <queue>
#include <climits> // 包含INT_MIN定义
using namespace std;
// 二叉树节点定义
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
// 创建队列用于BFS层序遍历
queue<TreeNode*> que;
// 如果根节点不为空,将其加入队列
if (root != NULL) que.push(root);
// 存储结果的向量,将保存每一层的最大值
vector<int> result;
// 当队列不为空时,继续遍历
while (!que.empty()) {
// 获取当前层的节点数量
int size = que.size();
// 初始化当前层的最大值
// 使用INT_MIN(最小整数值)作为初始值,确保任何节点值都会比它大
int maxValue = INT_MIN;
// 遍历当前层的所有节点
for (int i = 0; i < size; i++) {
// 取出队首节点
TreeNode* node = que.front();
que.pop();
// 更新当前层的最大值
// 如果当前节点值大于maxValue,则更新maxValue
// 这是条件运算符:condition ? expr1 : expr2
// 当node->val > maxValue为真时,返回node->val,否则返回maxValue
maxValue = node->val > maxValue ? node->val : maxValue;
// 将当前节点的左子节点加入队列(如果存在)
if (node->left) que.push(node->left);
// 将当前节点的右子节点加入队列(如果存在)
if (node->right) que.push(node->right);
}
// 将当前层的最大值加入结果数组
result.push_back(maxValue);
}
// 返回每层最大值的向量
return result;
}
};
// 测试代码
int main() {
// 构建测试二叉树: [1,3,2,5,3,null,9]
// 1
// / \
// 3 2
// / \ \
// 5 3 9
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(3);
root->right = new TreeNode(2);
root->left->left = new TreeNode(5);
root->left->right = new TreeNode(3);
root->right->right = new TreeNode(9);
Solution solution;
vector<int> result = solution.largestValues(root);
// 打印结果
cout << "每层最大值: ";
for (int val : result) {
cout << val << " ";
}
cout << endl;
// 预期输出: 1 3 9
// 清理内存
delete root->left->left;
delete root->left->right;
delete root->right->right;
delete root->left;
delete root->right;
delete root;
return 0;
}完整代码说明:
1. 必需的头文件:
-
#include <iostream>:输入输出流,用于打印结果 -
#include <vector>:使用vector容器存储结果 -
#include <queue>:使用queue进行BFS遍历 -
#include <climits>:包含INT_MIN的定义(也可以使用<limits.h>)
2. TreeNode结构体:
-
定义了二叉树节点的基本结构
-
包含三种构造函数:
-
默认构造函数:
val=0, left=nullptr, right=nullptr -
单参数构造函数:只设置val值
-
完整构造函数:设置所有成员
-
3. Solution类:
-
实现了
largestValues方法 -
使用BFS层序遍历二叉树
-
找出每层的最大值并存储到vector中
4. main函数(测试):
-
构建了一个测试二叉树
-
创建Solution对象并调用
largestValues方法 -
打印结果并验证
-
最后清理分配的内存
如果想使用std::max函数,可以包含<algorithm>头文件:
#include <algorithm> // 添加这个头文件可以使用max函数 // 然后修改更新最大值的代码: maxValue = max(maxValue, node->val); // 更简洁