今天继续整理一些关于算法竞赛中C++适用的一些模板以及思想。
保留x位小数
保留x位小数在C语言中可以使用printf中的"%.xf"来实现,但是很多C++选手由于关闭了同步流,害怕cin、cout与scanf、printf混用容易出错,所以就给大家介绍一个强制保留x位小数的代码格式。
cpp
cout<<fixed<<setprecision(x)<<(浮点型变量);其中的x可以根据题目中的要求更改,接下来看一道例题来对这个函数加深印象。
排队接水
题目链接:排队接水
排队接水问题是一个非常典型的贪心问题,其中贪心的过程就不过多赘述了,原则就是前面的人消耗的时间越多,后面所有人等待的时间就越多,所以要让耗时小的人在前面,这样来构成全局最优解。可以试想一下,同样是两个人,其中一个人需要1小时,另一个人需要10分钟,如果让耗时多的人先接水的话,总时间就是这个人的耗时 + 后面的人等待其接水的耗时 + 后面的人的耗时,所以要对耗时进行排序,根据贪心原则让耗时少的人先接水。
cpp
// Problem: P1223 排队接水
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1223
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
void solve()
{
int n;cin>>n;
vector<pii> a(n+1);
for(int i=1;i<=n;i++)
{
cin>>a[i].fi;
a[i].se = i;
}
sort(a.begin()+1,a.end());//贪心
double sum = 0,ans=0;
for(int i=1;i<=n;i++)
{
cout<<a[i].se<<' ';
if(i==n) break;//因为求的是等待时间 最后一个人不算
sum += a[i].fi;
ans += sum;
}
cout<<endl;
//保留2位小数!
cout<<fixed<<setprecision(2)<<ans/n;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
} 最长上升子序列
最长上升子序列是dp的一类入门题目,我在前面的博客中有做过对一些常见的线性DP的题型、用法以及模板内容的介绍,对这一块不熟悉的小伙伴可以去看一下:线性DP,对于最长上升子序列,如果求的是长度,可以用遍历 + 二分的方式降低时间复杂度,而如果是需要求出具体的以每一个元素结尾的长度的话就需要用到双重循环来解决了(当然也可以用时间复杂度更低的单调队列来解决,单调队列我也有过总结,感兴趣的小伙伴也可以去看一下总结的模板:入门,推广 具体情况视题目而定),接下来看一道相关的题目。
合唱队形
这道题用到了正向和逆向双向相结合的思路,这种思想特别重要!很多像单调栈、最长子段和之类的题目也会用到这样的思想,对于这道题而言我们需要正向用一遍最长上升子序列求出以每个点结尾的最长上升子序列的长度,然后逆向再跑一遍求出以每个元素开头的最长下降子序列的长度,然后再遍历一遍每个元素求出最大值,就是一共可以留下来的人数,题目中要求的移除的人数只需用总人数减去留下的人数即可得出。
cpp
// Problem: P1091 [NOIP 2004 提高组] 合唱队形
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1091
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
void solve()
{
int n;cin>>n;
vector<int> a(n+1);
for(int i=1;i<=n;i++) cin>>a[i];
int l[n+1],r[n+1];
// for(int i=1;i<=n;i++) l[i] = 1,r[i] = 1;
fill(l+1,l+1+n,1);
fill(r+1,r+1+n,1);
for(int i=2;i<=n;i++)//正序最长上升子序列
{
for(int j=1;j<i;j++)
if(a[j] < a[i]) l[i] = max(l[i],l[j] + 1);
}
for(int i=n-1;i>=1;i--)//逆序最长上升子序列(正序最长下降子序列)
{
for(int j=n;j>i;j--)
if(a[j] < a[i]) r[i] = max(r[i],r[j] + 1);
}
int mx = -inf;
for(int i=1;i<=n;i++)
{
mx = max(mx,r[i] + l[i] - 1);//减去重复计算的自己
}
cout<<n - mx<<endl;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
} 归并排序
相信部分C++选手对排序并不感兴趣,因为STL中有自带的搞笑的sort排序,在nlogn的时间复杂度下满足了很多场景的需要,但是,归并排序的时间复杂度也是nlogn,而且有很多题型都用到了类似于归并排序中的分治思想,即将大问题转化为很多个小问题,然后通过对小问题的高效解决来使得总问题的解决的思想,其中较为典型的就是逆序对问题,这个问题就是在归并排序的合并过程中完成的!下面来回顾一下归并排序的代码以及对逆序对这一问题的高效求解。
逆序对
题目链接:逆序对
我们对逆序对的寻找不需要每次都遍历计数,而是可以先将集合分为两个部分,而这两个部分又是有序的两个集合,我们可以对两个集合的元素进行比较大小的同时用O(1)的方法计算逆序对的数量,在合并的过程中如果左边的集合中的元素小,直接将左边这个元素合并上去,反之如果左边的元素大,就应该将右边的元素合并上去,而此时左边剩余元素的数量就是以右边的这个较小的数位第二个数的逆序对的数量,所以能在归并排序合并过程的同时就将逆序对的数量进行统计了。代码如下所示:
cpp
// Problem: P1908 逆序对
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1908
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 5e5+10;
vector<int> a(N,0),b(N,0);
int res=0;
void gb_sort(int l,int r)
{
if(l >= r) return ;
int mid = (l + r) >> 1;
gb_sort(l,mid);
gb_sort(mid+1,r);//分治过程
int i=l,j=mid+1,k=l;//分治过程
while(i <=mid && j <= r)//归并过程
{
if(a[i] <= a[j]) b[k++] = a[i++];
else b[k++] = a[j++],res += mid - i + 1;
}
while(i <= mid) b[k++] = a[i++];//对剩余元素的处理
while(j <= r) b[k++] = a[j++];//对剩余元素的处理
for(int i=l;i<=r;i++) a[i] = b[i];//将排序后的数组保存
}
void solve()
{
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
gb_sort(1,n);
// for(int i=1;i<=n;i++) cout<<a[i]<<' ';
cout<<res<<endl;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
} 高精度运算
C/C++选手的痛!在蓝桥杯等一些赛事中经常出现,高精度和低精度之间的混合运算比较简单,正常模拟即可,我也有过总结,需要的小伙伴可以去主页拿。这里主要整理高精度乘高精度下的快速幂。
麦森数
题目链接:麦森数
这道题的数据范围比较大,不仅仅用到了高精度✖️高精度,还需要用快速幂来优化,因为是2的n次方所以就要想到了以2位初始值的快速幂,又因为数太大了(光看样例就已经很恐怖了)所以就又想到了高精度,这时候整体的代码思路就出来了,实现起来也不难,整理这道题的主要原因就是便于对之后的快速幂以及高精度算法模板的需要,有需要的小伙伴也可以保存起来以后备用。
cpp
// Problem: P1045 [NOIP 2003 普及组] 麦森数
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1045
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 505;
vector<int> a(N,0),res(N,0);
void gjc_begin()
{
int t=0,c=0;
vector<int> temp(1010,0);
for(int i=1;i<=500;i++)
{
for(int j=1;j<=500;j++) temp[i+j-1] += a[i] * a[j];
}
for(int i=1;i<=500;i++)
{
temp[i] += t;
a[i] = temp[i] % 10;
t = temp[i] / 10;
}
}
void gjc_end()
{
int t=0,c=0;
vector<int> temp(1010,0);
for(int i=1;i<=500;i++)
{
for(int j=1;j<=500;j++) temp[i+j-1] += res[i] * a[j];
}
for(int i=1;i<=500;i++)
{
temp[i] += t;
res[i] = temp[i] % 10;
t = temp[i] / 10;
}
}
void ksm_plus(int x)
{
while(x)
{
if(x&1) gjc_end();
gjc_begin();
x >>= 1;
}
}
void solve()
{
int n;cin>>n;
a[1] = 2,res[1] = 1;//快速幂的初始值位2 因为要求的是2的次方
ksm_plus(n);
int num=0;
//数学公式直接计算2^n的位数
cout<<(int)(n*log10(2) + 1)<<endl;
int cnt=0;
int t = 1;
while(res[t] == 0)//对最后的 -1 操作进行计算
{
res[t] = 9;
t++;
}
res[t]--;
for(int i=500;i>0;i--)
{
cout<<res[i];
cnt++;
if(cnt == 50)
{
cout<<endl;
cnt = 0;
}
}
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
} 求位数的高效方法
求x的位数相信很很堵人都会了,用 (int)log10(x) + 1即可,也可转为字符串求长度。
这道题还需要用到的数学知识就是2的n次方的位数,如果用模拟法计算的话还需要用到高精度算法,而如果使用数学方法的话就很方便了,而且时间复杂度也不高,具体实现公式为:
cpp
(int)(n*log10(2) + 1)倍增法
倍增法也是一个常用的算法,其中在求最近共同祖先的时候最为有用,可以将每次的O(N)时间复杂度的查询压缩至单次O(logN)的时间复杂度,适用于多次查询最近共同祖先(LCA)的情况,具体思路如下:其中数组f[n][m]表示n的第2^m级祖先, 最重要的是在dfs求深度时对倍增ST表进行预处理

图中左侧位预处理阶段,右侧为查询LCA阶段。
LCA最近共同祖先
题目链接:LCA最近共同祖先【模板】
为了方便之后对这一块模板代码的内容进行整理,所以我在这里用一个模版题来对倍增法求LCA做一个记录,如果之后有需要的话可以参考这个模板。
cpp
// Problem: P3379 【模板】最近公共祖先(LCA)
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3379
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 500010;
int n,m,s;
vector<int> a[N];
int dep[N],fu[N][30];
void dfs(int x,int fa)//深搜预处理阶段
{
dep[x] = dep[fa] + 1;
fu[x][0] = fa;
for(int i=1;i<30;i++) fu[x][i] = fu[fu[x][i-1]][i-1];//祖先预处理阶段
for(auto i : a[x])
{
if(i == fa) continue;//无向边所以都存,防止重复访问父节点
dfs(i,x);
}
}
int LCA(int x,int y)
{
if(dep[x] < dep[y]) swap(x,y);
while(dep[x] > dep[y]) x = fu[x][(int)log2(dep[x] - dep[y])];//先移动到同一层
if(x == y) return x;//移动到同一层就重合了说明这个就是祖先了
for(int i=log2(dep[x]);i>=0;i--)//根据二进制(2的幂次方)分解找到LCA的下一层(子节点)
{
if(fu[x][i] != fu[y][i])是共同祖先但是要保证是最近的所以在没找到时才更新
{
x = fu[x][i];
y = fu[y][i];
}
}
return fu[x][0];//这一层的上一层就是LCA
}
void solve()
{
cin>>n>>m>>s;
for(int i=1;i<n;i++)
{
int u,v; cin>>u>>v;
a[u].push_back(v);
a[v].push_back(u);
}
dfs(s,0);
while(m--)
{
int x,y;cin>>x>>y;
cout<<LCA(x,y)<<endl;
}
// cout<<fixed<<setprecision(x)<< ;
}
signed main()// Don't forget pre_handle!
{
IOS
int T=1;
// cin>>T;
while(T--) solve();
return 0;
} [eJOI 2020] Fountain (Day1)
题目链接:[eJOI 2020] Fountain (Day1)
这道题是很好的一道题,他不仅仅考察了对倍增的运用,而且还考察了单调栈。废话不多说,接下来就来看一下这道题的详细解析。
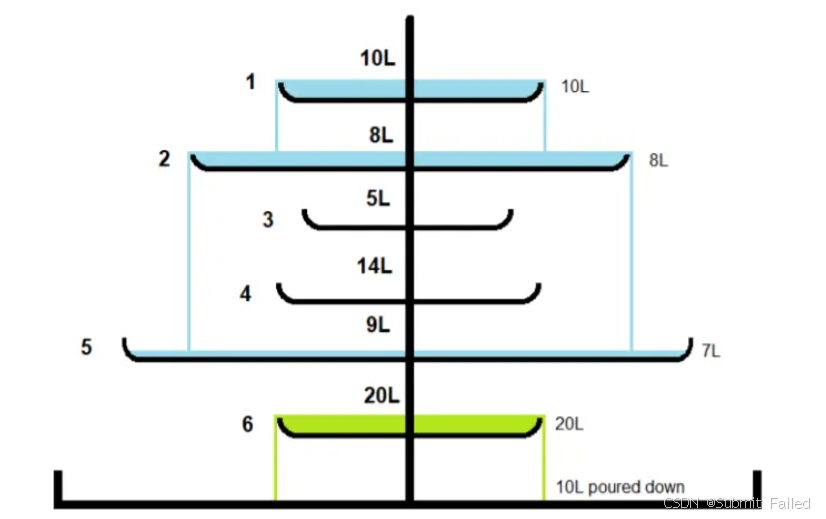
首先看到这到题第一反应就是从这个位置开始一直找后面的比当前元素要大的位置,然后不断的更新value,最后到哪一个地方value小于或等于这里的盘子了就说明找到最终的答案了但是每次都遍历所有的点就会超时,那么我们就开始想怎么去优化,我们首先可以想到用单调栈来记录每一个元素下边的第一个大于他的元素(等于不行!)这样就不用每次都从当前点来事遍历找第一个大于他的点了,只需要O(n)的复杂度就能处理完这一操作,但是这就完了吗,交上去发现只有30分,还能怎么优化呢?我们想既然有了单调性的话,能不能用二分,可是二分还需要知道每一段的容量,也不好求,我们既然是从当前开始一直找到下一个大于当前的点,那我们是否可以跳着找呢,跳着找第2的幂次方个大于他的盘子,用倍增ST表来解决呢?灵感来源于:
所以我们可以先用单调栈(因为是右边第一个大于他的元素,所以用逆序遍历的单调递减栈来实现,对单调栈这一方面不熟悉的小伙伴可以去看我的单调栈知识点的总结:单调栈详解)来处理每一段单调递增的盘子,然后将他们建树,这样就可以用倍增法来实现跳着找了。
将🌳建起来大概是这样,相信大家能够更形象地理解:
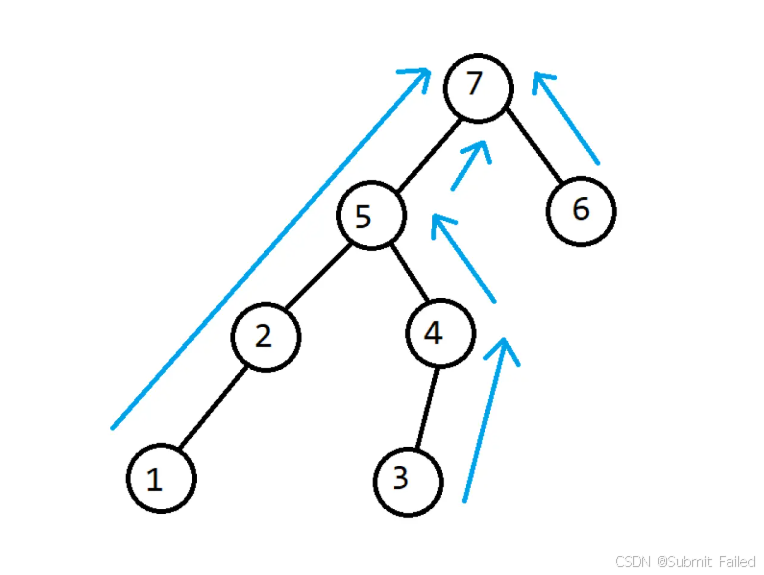
代码如下:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f; // 无穷大
const int N = 1e5 + 10;
// 定义各数组和变量
vector<int> a(N,0),v(N,0),r(N,0); // a存储直径,v存储容量,r存储右侧第一个大于当前直径的喷泉编号
stack<int> st; // 单调栈
int n,m; // n个喷泉,m次查询
vector<int> e[N]; // 邻接表存储树结构
vector<int> dep(N,0); // 存储每个节点的深度
int fu[N][30],g[N][30]; // fu[i][j]表示i节点向上2^j层的祖先,g[i][j]表示i节点向上2^j层的容量和
// DFS预处理倍增数组
void dfs(int x,int fa)
{
dep[x] = dep[fa] + 1; // 计算当前节点深度
fu[x][0] = fa,g[x][0] = v[fa]; // 初始化直接父节点和容量
// 预处理倍增数组
for(int i=1;i<30;i++)
{
fu[x][i] = fu[fu[x][i-1]][i-1];// 计算祖先
g[x][i] = g[fu[x][i-1]][i-1] + g[x][i-1];// 计算容量和
}
// 递归处理子节点
for(auto i : e[x]) dfs(i,x);
}
void solve()
{
cin>>n>>m;
// 设置哨兵节点
a[n+1] = inf,v[n+1] = inf; // 第n+1个喷泉作为边界
// 输入每个喷泉的直径和容量
for(int i=1;i<=n;i++) cin >> a[i] >> v[i];
// 单调栈处理,找到每个喷泉右侧第一个直径大于它的喷泉
for(int i=n;i>=1;i--)
{
// 维护单调递减栈
while(!st.empty() && a[st.top()] <= a[i]) st.pop();
// 如果栈空则指向哨兵,否则指向栈顶
r[i] = (st.empty() ? n+1 : st.top());
st.push(i); // 当前喷泉入栈
}
// 构建树结构
for(int i=n;i>=1;i--) e[r[i]].push_back(i);
// 从哨兵节点开始DFS预处理
dfs(n+1,0);
// 处理查询
for(int i=1;i<=m;i++)
{
int index,value; cin>>index>>value;
// 如果当前喷泉容量足够
if(v[index] >= value)
{
cout<<index<<endl;
continue;
}
// 否则减去当前喷泉的容量
value -= v[index];
int x=index;int ans=0;
// 倍增查找能容纳剩余水量的最低祖先
for(int i=25;i>=0;i--)
{
if(g[x][i] <= value && (1LL<<i) <= dep[x])
{
value -= g[x][i];
x = fu[x][i];
}
if(value == 0) ans = x;
}
// 如果还有剩余水量,再向上走一步
if(ans == 0) ans = fu[x][0];
// 输出结果,如果是哨兵则输出0
if(ans == n+1) cout<<0<<endl;
else cout<<ans<<endl;
}
}
signed main()
{
IOS // 加速输入输出
int T=1;
while(T--) solve();
return 0;
}之后的算法思维以及解题方法总结都会在本文进行更新,有兴趣对这一块内容进行整理的小伙伴可以保存起来。
