开发也能看懂的大模型：聚类

聚类（Clustering）简介

聚类是一种 无监督学习方法 ，用于将数据集划分为多个 组（簇，Clusters） ，使得组内样本之间的相似性尽可能高，组间样本的差异性尽可能大。它常用于数据探索、模式发现和降维。

---

1. 聚类的基本原理

• 目标：将未标注的数据集划分成若干簇，使得：

  • 同一簇内的样本尽可能相似（簇内紧凑性高）。
  • 不同簇之间的样本尽可能不同（簇间分离性强）。

• 常用距离度量：衡量样本之间的相似性或差异性。

  • 欧几里得距离
  • 曼哈顿距离
  • 余弦相似度
  • Jaccard 相似系数

---

2. 常见的聚类算法

（1）K-Means

• 原理：通过迭代，将数据点分配到最近的中心，并更新中心点位置，直到收敛。

• 特点：

  • 简单高效，但对初始点敏感。
  • 适合处理形状为球形的簇，且对噪声和异常值较敏感。

• 参数：需指定簇数 k。

---

（2）层次聚类（Hierarchical Clustering）

• 原理：

  • 凝聚层次聚类：从每个点开始，每次合并最近的两个簇，直至形成一棵树。
  • 分裂层次聚类：从整体开始，每次拆分最不相似的簇，直至每个样本独立为一簇。

• 特点：

  • 不需要指定簇数。
  • 可以生成树状结构（树状图）。
  • 计算复杂度较高，不适合大规模数据。

---

（3）DBSCAN（Density-Based Spatial Clustering of Applications with Noise）

• 原理：基于密度的聚类方法，按照样本点的密度分布识别簇，同时将低密度区域的点标记为噪声。

• 特点：

  • 自动确定簇数。
  • 对非球形簇效果好。
  • 能处理噪声和异常值。

• 适用场景：地理位置聚类、密度差异明显的数据。

---

（4）高斯混合模型（Gaussian Mixture Model, GMM）

• 原理：假设数据是由多个高斯分布混合而成，通过最大化似然估计找到每个高斯分布的参数，进行软聚类。

• 特点：

  • 与 K-Means 不同，可以进行 软聚类（一个点可以属于多个簇）。
  • 适合处理椭圆形或复杂分布的簇。

---

（5）Mean-Shift

• 原理：通过滑动窗口找到密度最大的区域，每次迭代移动到密度中心，最终将点分配到密度吸引的簇中。

• 特点：

  • 不需要指定簇数。
  • 对非球形簇效果好。
  • 计算复杂度较高。

---

3. 聚类评估指标

由于聚类是无监督学习，评估其效果需要特定的指标：

内在评估

• 轮廓系数（Silhouette Coefficient） ：衡量样本在所属簇和最近簇之间的紧密性和分离性。

• 簇内方差（Inertia） ：衡量簇内样本与簇中心的平方和距离。

外在评估

如果有已知标签，可以用分类指标评估聚类效果：

• 纯度（Purity） ：聚类结果中主类样本占比。
• 调整兰德指数（ARI, Adjusted Rand Index） ：度量聚类与真实标签的相似性，值范围 [-1, 1]。

---

4. 实际应用

1. 客户细分：在电商、银行中根据用户行为特征划分客户群体。
2. 图像分割：通过像素特征对图像区域进行聚类。
3. 文档分类：根据文本相似性将文档聚类。
4. 推荐系统：基于用户偏好分组，为组内成员推荐类似的产品。
5. 生物信息学：基因表达聚类，发现生物学模式。

---

5. 使用示例：K-Means 聚类

1. 问题背景

假设我们有一组二维数据点，需要将这些点分成几个簇。每个簇代表一类相似的数据。

目标：利用 K-Means 算法对数据点进行聚类，并直观展示其聚类结果和算法步骤。

---

2. 数据生成与预处理

我们使用 make_blobs 方法生成二维数据，其中每个簇具有高斯分布，易于观察和分析。

import numpy as np
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成示例数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# 可视化数据点
plt.scatter(X[:, 0], X[:, 1], s=50, cmap='viridis')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

• 解释：

  • n_samples=300：生成 300 个样本。
  • centers=4：数据分布在 4 个中心点附近。
  • cluster_std=0.6：每个簇的标准差，决定点的分散程度。
  • random_state=42：随机种子，确保每次生成的数据一致。

运行后，我们会看到一个随机分布的二维数据集，其中点主要集中在 4 个簇附近。

---

3. K-Means 聚类

接下来使用 KMeans 进行聚类，分析其关键流程：

from sklearn.cluster import KMeans

# K-Means 聚类
kmeans = KMeans(n_clusters=4, random_state=42)
y_pred = kmeans.fit_predict(X)

# 聚类中心
centers = kmeans.cluster_centers_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=50)
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X')
plt.title('K-Means Clustering')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

---

4. 代码解析

1. 初始化：

   kmeans = KMeans(n_clusters=4, random_state=42)

   • n_clusters=4：指定聚类的簇数为 4。
   • random_state=42：设置随机种子，保证实验结果的可重复性。

2. 拟合与预测：

   y_pred = kmeans.fit_predict(X)

   • fit_predict 方法会执行两个任务：

     1. 拟合：根据数据找到最佳的簇中心。
     2. 预测：为每个数据点分配所属簇的标签。

3. 聚类中心：

   centers = kmeans.cluster_centers_

   • 返回聚类后每个簇的中心坐标。
   • 在结果中标记为红色 "X"。

---

K-Means 的聚类过程分为以下几步：

1. 初始化： 随机选择 4 个点作为初始聚类中心。
2. 点分配： 计算每个点到各聚类中心的距离，将点分配到最近的簇。
3. 中心更新： 对每个簇，重新计算其中心点（即簇内所有点的均值）。
4. 迭代： 重复步骤 2 和 3，直到聚类中心收敛或达到最大迭代次数。

---

可视化结果

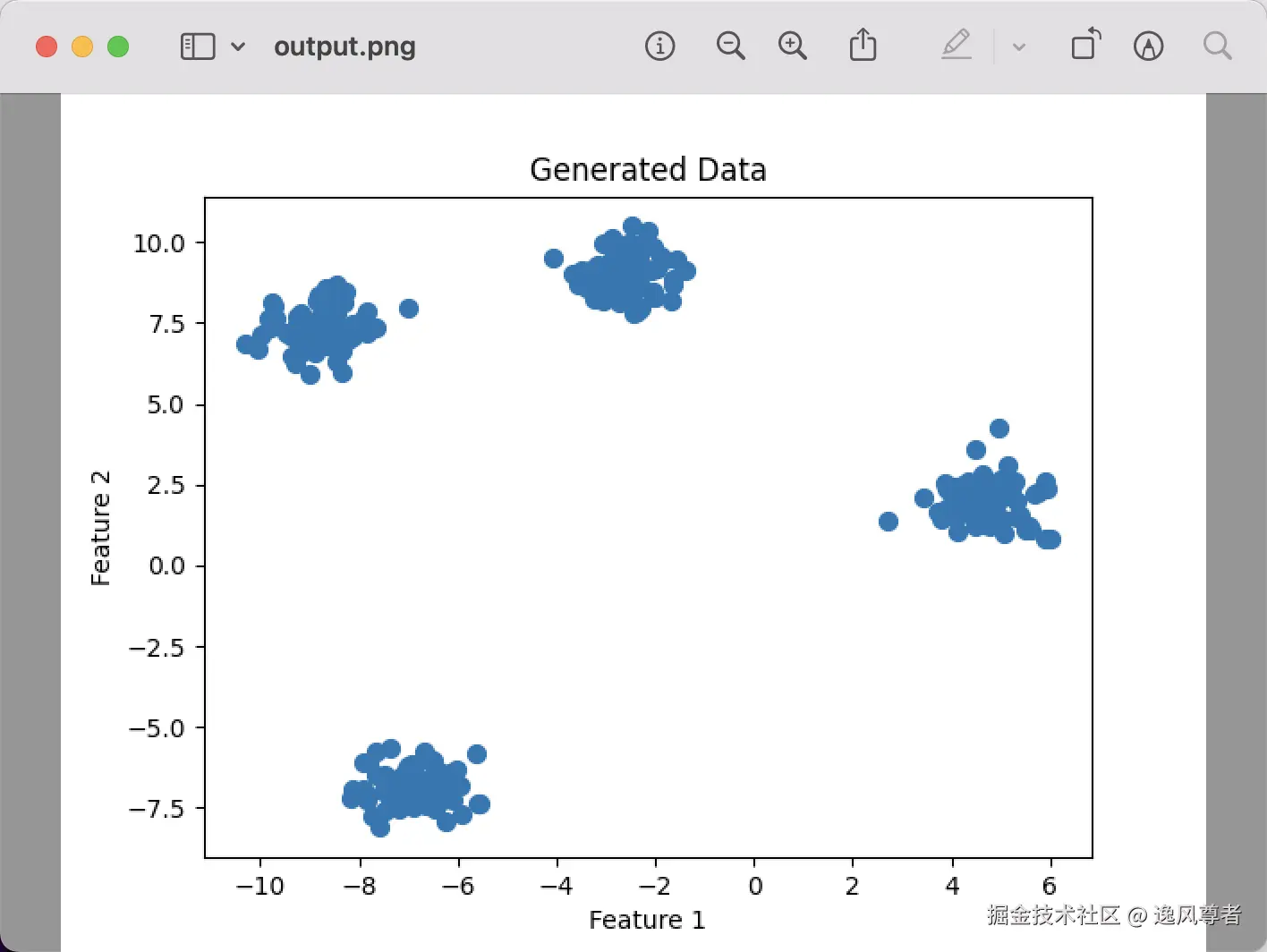
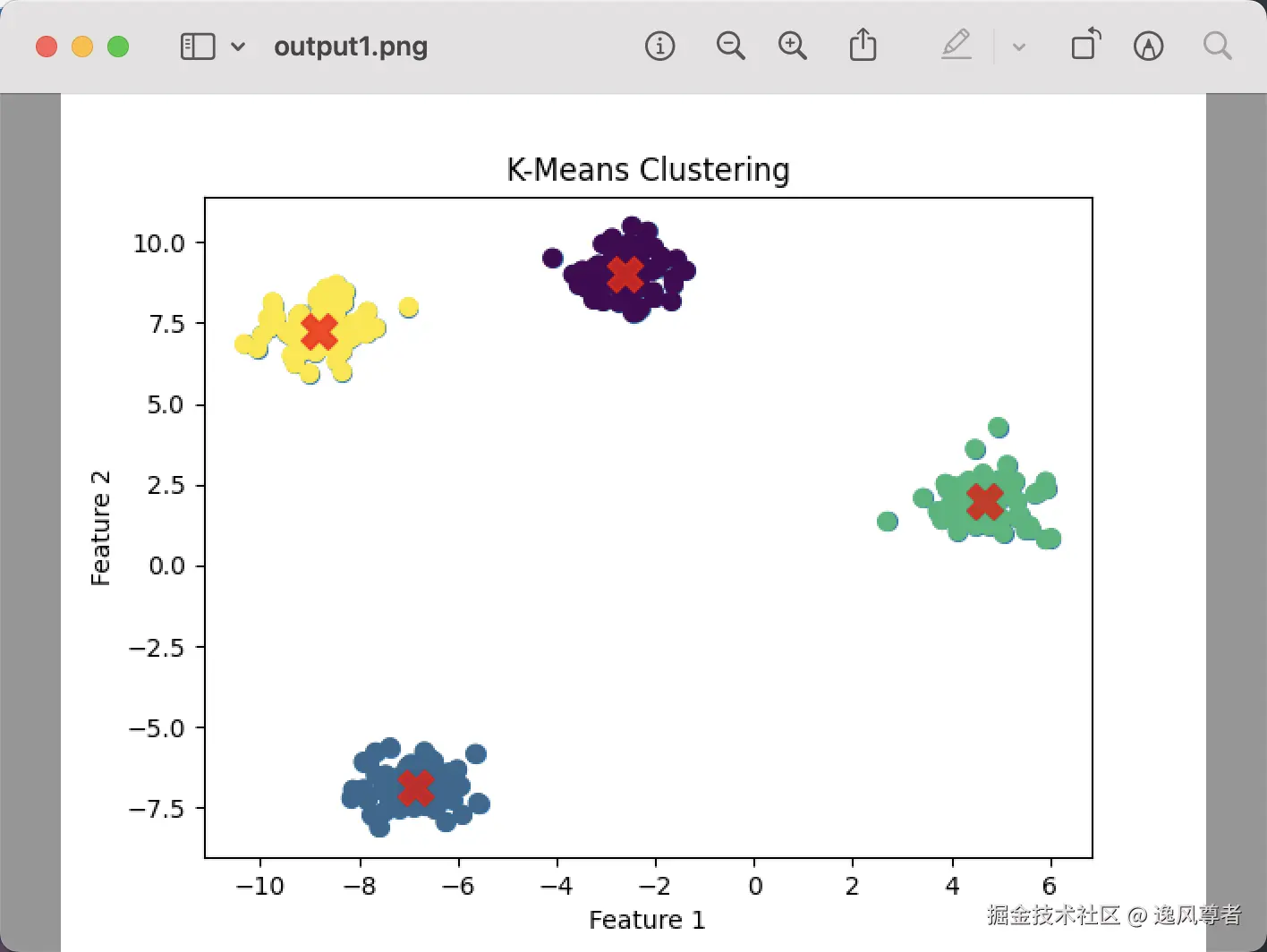
• 图1中点的颜色表示它们所属的簇。
• 图2中红色 "X" 标记了聚类后计算出的中心点。
• 数据点的分布与聚类结果较好地匹配，说明 K-Means 成功划分出了合理的簇。

---

完整代码：

import numpy as np
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 生成示例数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# 可视化数据点
plt.scatter(X[:, 0], X[:, 1], s=50, cmap='viridis')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.savefig('output.png')


# K-Means 聚类
kmeans = KMeans(n_clusters=4, random_state=42)
y_pred = kmeans.fit_predict(X)

# 聚类中心
centers = kmeans.cluster_centers_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=50)
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X')
plt.title('K-Means Clustering')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.savefig('output1.png')

---

5. 扩展：使用肘部法则确定簇数

KMeans中n_clusters参数的选择非常重要，过大或过小都会影响聚类效果。可以用肘部法则寻找最优值。

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 生成示例数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# 使用肘部法则和 Silhouette 分数确定最优 K 值
distortions = []
silhouette_scores = []
K = range(2, 10)

for k in K:
    kmeans = KMeans(n_clusters=k, random_state=42)
    y_pred = kmeans.fit_predict(X)
    distortions.append(kmeans.inertia_)
    silhouette_scores.append(silhouette_score(X, y_pred))

# 绘制结果
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(K, distortions, marker='o')
plt.title("Elbow Method")
plt.xlabel("Number of Clusters")
plt.ylabel("Distortion")

plt.subplot(1, 2, 2)
plt.plot(K, silhouette_scores, marker='o', color='green')
plt.title("Silhouette Score")
plt.xlabel("Number of Clusters")
plt.ylabel("Silhouette Score")

plt.tight_layout()
plt.savefig('output3.png')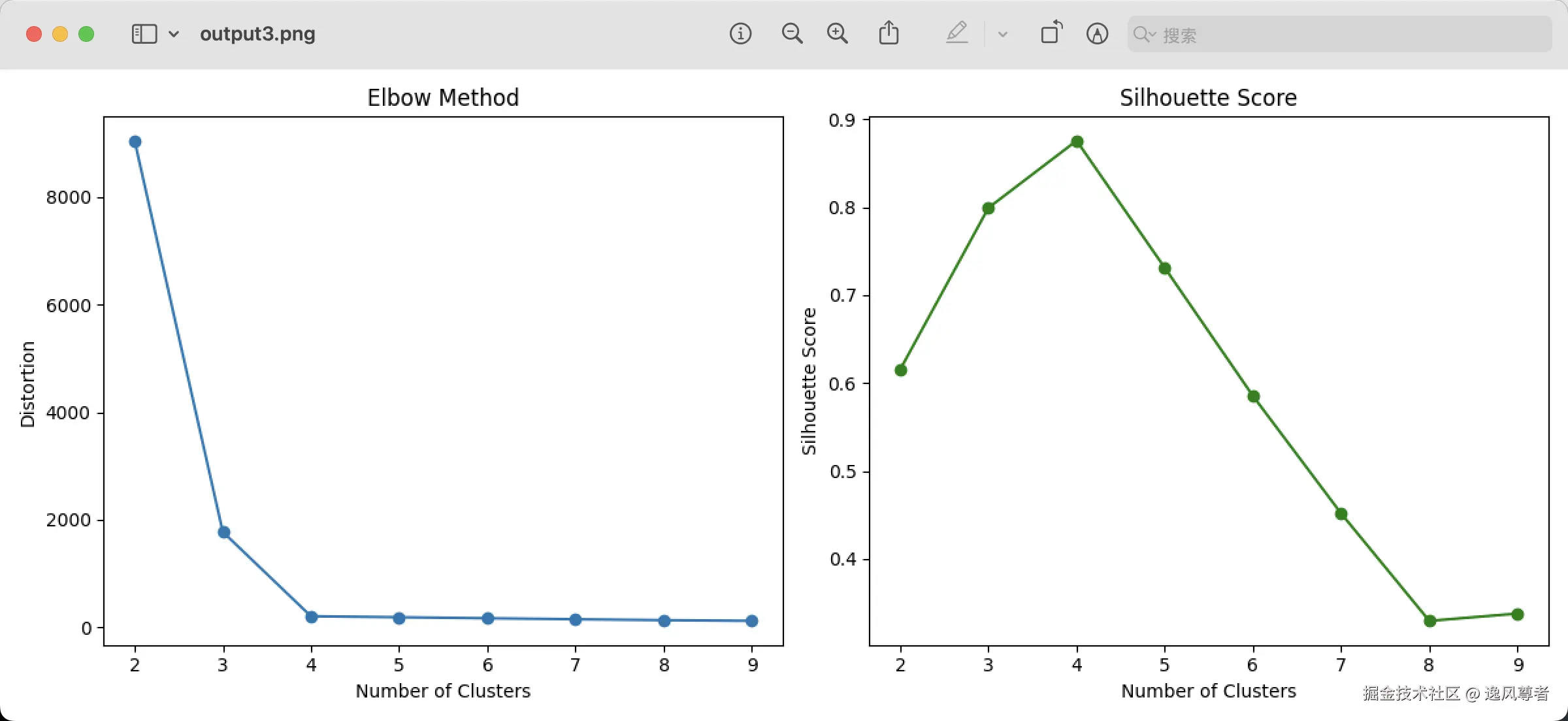

• Elbow Method：观察拐点位置选择 K。
• Silhouette Score：越高说明聚类效果越好。

---