文章目录
- 先言
- 一、特征工程概述
- 二、特征提取
-
- 1.字典特征提取(特征离散化)
- 2.文本特征提取
- [3.TfidfVectorizer TF-IDF文本特征词的重要程度特征提取](#3.TfidfVectorizer TF-IDF文本特征词的重要程度特征提取)
- 三、数据归一化与标准化
-
- [1.MinMaxScaler 归一化(Min-Max Scaling):(适合分布有界的数据)](#1.MinMaxScaler 归一化(Min-Max Scaling):(适合分布有界的数据))
- [2.normalize归一化(Normalize Scaling):(适合分布有界的数据)](#2.normalize归一化(Normalize Scaling):(适合分布有界的数据))
- [3.标准化(Z-Score Scaling):StandardScaler(适合高斯分布数据)](#3.标准化(Z-Score Scaling):StandardScaler(适合高斯分布数据))
- 四、特征选择与降维
-
- 1.方差阈值法(VarianceThreshold)剔除低方差特征
- [2.皮尔逊相关系数(Pearson correlation coefficient)](#2.皮尔逊相关系数(Pearson correlation coefficient))
- 3.主成分分析(sklearn.decomposition.PCA)
- 结语
先言
在机器学习项目中,数据和特征决定了模型性能的上限,而优秀的特征工程能让我们逼近这个上限。特征工程是从原始数据中提取、转换和优化特征的过程,直接影响模型的准确性、泛化能力和训练效率。
本文将深入探讨特征工程的核心技术包括:字典特征提取(DictVectorizer)、文本特征处理(词袋模型、TF-IDF)、数据标准化与归一化(StandardScaler, MinMaxScaler)、特征降维(低方差过滤、PCA主成分分析)。通过理论讲解与代码实战,帮助你掌握如何将原始数据转化为高质量特征,为机器学习模型提供更强大的输入!
一、特征工程概述
什么是特征工程?为什么它如此重要?
特征工程:就是对特征进行相关的处理
一般使用pandas来进行数据清洗和数据处理、使用sklearn来进行特征工程
特征工程是将任意数据(如文本或图像)转换为可用于机器学习的数字 特征,比如:字典特征提取(特征离散化)、文本特征提取、图像特征提取。
特征工程步骤为:
- 特征提取, 如果不是像dataframe那样的数据,要进行特征提取,比如字典特征提取,文本特征提取
- 无量纲化(预处理)
- 归一化
- 标准化
- 降维
- 底方差过滤特征选择
- 主成分分析-PCA降维
二、特征提取
特征提取旨在从原始特征中提取出新的、更具表达力的特征。
1.字典特征提取(特征离散化)
sklearn.feature_extraction.DictVectorizer(sparse=True)参数:
sparse=True返回类型为csr_matrix的稀疏矩阵
sparse=False表示返回的是数组,数组可以调用.toarray()方法将稀疏矩阵转换为数组
-
转换器对象:
转换器对象调用fit_transform(data)函数,参数data为一维字典数组或一维字典列表,返回转化后的矩阵或数组
转换器对象get_feature_names_out()方法获取特征名
代码如下(示例):
python
from sklearn.feature_extraction import DictVectorizer
import pandas as pd
data = [{'city':'成都', 'age':30, 'temperature':200}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80}]
#创建字典列表特征提取对象
transfer = DictVectorizer(sparse=False)
#调用fit_transform方法,获取转换后的特征数组
data_new = transfer.fit_transform(data)
#打印特征数组
print(data_new)
#获取特性名称
print(transfer.get_feature_names_out())[[ 30. 0. 1. 0. 200.]
[ 33. 0. 0. 1. 60.]
[ 42. 1. 0. 0. 80.]]
['age' 'city=北京' 'city=成都' 'city=重庆' 'temperature']当sparse=True时,返回一个三元组的稀疏矩阵:
python
#获取稀疏矩阵
transfer = DictVectorizer(sparse=True)
data_new = transfer.fit_transform(data)
#返回一个三元组稀疏矩阵
print(data_new)返回数据结果如下:
<Compressed Sparse Row sparse matrix of dtype 'float64'
with 9 stored elements and shape (3, 5)>
Coords Values
(0, 0) 30.0
(0, 2) 1.0
(0, 4) 200.0
(1, 0) 33.0
(1, 3) 1.0
(1, 4) 60.0
(2, 0) 42.0
(2, 1) 1.0
(2, 4) 80.0三元组表 (Coordinate List, COO):三元组表就是一种稀疏矩阵类型数据,存储非零元素的行索引、列索引和值:
(行,列) 数据
(0,0) 10
(0,1) 20
(2,0) 90
(2,20) 8
(8,0) 70
表示除了列出的有值, 其余全是0
我们可以对三元组表进行转换为数组形式,可上面的数组一致,只不过通过三元组对数据进行获取可以节省资源,示例代码:
python
#对三元组矩阵进行转换
data_new = data_new.toarray()
print(data_new)
print(transfer.get_feature_names_out())返回结果如下:
[[ 30. 0. 1. 0. 200.]
[ 33. 0. 0. 1. 60.]
[ 42. 1. 0. 0. 80.]]
['age' 'city=北京' 'city=成都' 'city=重庆' 'temperature']补充(稀疏矩阵):
稀疏矩阵
稀疏矩阵是指一个矩阵中大部分元素为零,只有少数元素是非零的矩阵。在数学和计算机科学中,当一个矩阵的非零元素数量远小于总的元素数量,且非零元素分布没有明显的规律时,这样的矩阵就被认为是稀疏矩阵。例如,在一个1000 x 1000的矩阵中,如果只有1000个非零元素,那么这个矩阵就是稀疏的。
由于稀疏矩阵中零元素非常多,存储和处理稀疏矩阵时,通常会采用特殊的存储格式,以节省内存空间并提高计算效率。
2.文本特征提取
sklearn.feature_extraction.text.CountVectorizer构造函数关键字参数stop_words,值为list,表示词的黑名单(不提取的词)
fit_transform函数的返回值为稀疏矩阵
2.1英文文本提取
代码如下(示例):
python
from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
import jieba
data=["stu is well, stu is great", "You like stu"]
#创建转换器
transfer = CountVectorizer()
#调用fit_transform方法进行提取
data_new = transfer.fit_transform(data)
#返回的数组数字代表词频
print(data_new.toarray())
#获取特征名称
print(transfer.get_feature_names_out())
#使用pandas创建字典列表
data = pd.DataFrame(data_new.toarray(),columns=transfer.get_feature_names_out(),index=['sentence1','sentence2'])
print(data)返回结果:
[[1 2 0 2 1 0]
[0 0 1 1 0 1]]
['great' 'is' 'like' 'stu' 'well' 'you']
great is like stu well you
sentence1 1 2 0 2 1 0
sentence2 0 0 1 1 0 12.2中文文本提取(jieba分词器)
代码如下(示例):
python
#中文文本提取
data = ["小明喜欢小张","小张喜欢小王","小王喜欢小李"]
#创建中文文本分割函数
def chinese_word_cut(mytext):
return " ".join(jieba.cut(mytext))
data1 = [chinese_word_cut(i) for i in data]
# print(data1)
#创建词频统计对象
transfer = CountVectorizer()
data_new = transfer.fit_transform(data1)
print(data_new.toarray())
print(transfer.get_feature_names_out())返回结果:
[[1 1 1 0 0]
[1 1 0 0 1]
[1 0 0 1 1]]
['喜欢' '小张' '小明' '小李' '小王']补充:jieba是一个工具库可以通过pip下载,jieba用于对中文进行自动分词对于自然语言方面一个不错的分词工具
3.TfidfVectorizer TF-IDF文本特征词的重要程度特征提取
词频(Term Frequency, TF), 表示一个词在当前篇文章中的重要性
逆文档频率(Inverse Document Frequency, IDF), 反映了词在整个文档集合中的稀有程度

代码与CountVectorizer的示例基本相同,仅仅把CountVectorizer改为TfidfVectorizer即可,代码如下(示例):
python
import jieba
import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.preprocessing import normalize
def chinese_word_cut(mytext):
return " ".join(jieba.cut(mytext))
data = [
"量子纠缠是物理学中一种奇妙的现象,两个粒子即使相隔遥远也能瞬间影响彼此的状态。",
"今天早上我吃了一个苹果,然后去公园散步,看到很多人在跳舞。",
"䴖䴗䴘䴙䴚䴛是一些非常罕见的汉字,它们属于 Unicode 扩展字符集。"
]
#通过jieba对数据进行分词
data1 = [chinese_word_cut(i) for i in data]
#创建文字稀有度统计对象
transfer =TfidfVectorizer()
#调用对象方法转换数据
data_new = transfer.fit_transform(data1)
print(data_new.toarray())
print(transfer.get_feature_names_out())
data_new = MyTfidfVectorizer(data1)
print(data_new)提取结果:
[[0. 0. 0. 0.25819889 0.25819889 0.
0. 0.25819889 0.25819889 0. 0. 0.
0.25819889 0.25819889 0. 0. 0. 0.
0. 0. 0.25819889 0.25819889 0.25819889 0.25819889
0. 0.25819889 0.25819889 0.25819889 0. 0.
0. 0.25819889 0.25819889 0. ]
[0. 0.31622777 0. 0. 0. 0.31622777
0.31622777 0. 0. 0. 0. 0.
0. 0. 0.31622777 0. 0.31622777 0.31622777
0. 0.31622777 0. 0. 0. 0.
0.31622777 0. 0. 0. 0. 0.31622777
0.31622777 0. 0. 0. ]
[0.33333333 0. 0.33333333 0. 0. 0.
0. 0. 0. 0.33333333 0.33333333 0.33333333
0. 0. 0. 0.33333333 0. 0.
0.33333333 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.33333333 0.
0. 0. 0. 0.33333333]]
['unicode' '一个' '一些' '一种' '两个' '今天' '公园' '即使' '奇妙' '字符集' '它们' '属于' '影响'
'彼此' '很多' '扩展' '散步' '早上' '汉字' '然后' '物理学' '状态' '现象' '相隔' '看到' '瞬间' '粒子'
'纠缠' '罕见' '苹果' '跳舞' '遥远' '量子' '非常']自己函数实现重要程度特征提取(有兴趣的可以看看):
python
def MyTfidfVectorizer(data):
#提取词频TF
transfer = CountVectorizer()
data_new = transfer.fit_transform(data)
TF = data_new.toarray()
#提取IDF
IDF = np.log((len(TF)+1)/(np.sum(TF!=0,axis=0)+1))+1
tf_idf = TF*IDF
#l2归一化
tf_idf =normalize(tf_idf,norm='l2')
return tf_idf
data_new = MyTfidfVectorizer(data1)
print(data_new)执行后连着的结果是一样的
三、数据归一化与标准化
通过对原始数据进行变换把数据映射到指定区间(默认为0-1)
归一化公式:
1.MinMaxScaler 归一化(Min-Max Scaling):(适合分布有界的数据)
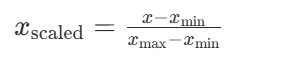
这里的 𝑥min 和 𝑥max 分别是每种特征中的最小值和最大值,而 𝑥是当前特征值,𝑥scaled 是归一化后的特征值。
若要缩放到其他区间,可以使用公式:x=x*(max-min)+min;
比如 [-1, 1]的公式为:
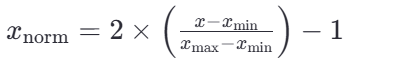
sklearn.preprocessing.MinMaxScaler(feature_range)参数:feature_range=(0,1) 归一化后的值域,可以自己设定
fit_transform函数归一化的原始数据类型可以是list、DataFrame和ndarray, 不可以是稀疏矩阵
fit_transform函数的返回值为ndarray
代码如下(示例):
python
#获取数据集
iris = load_iris()
data = iris.data[:5]
print(data)
#最大最小值归一化(MinMaxScaler)
#创建MinMaxScaler对象
transfer1 =MinMaxScaler()
#对数据进行规划处理
data_new = transfer1.fit_transform(data)
print(data_new)这里是以鸢尾花数据为例:
初始数据
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
归一化后数据
[[1. 0.83333333 0.5 0. ]
[0.6 0. 0.5 0. ]
[0.2 0.33333333 0. 0. ]
[0. 0.16666667 1. 0. ]
[0.8 1. 0.5 0. ]]2.normalize归一化(Normalize Scaling):(适合分布有界的数据)
sklearn.preprocessing.normalize(data, norm='l2', axis=1)- norm表述normalize标准化的三种方式
<1> L1归一化(norm=l1):绝对值相加作为分母,特征值作为分子
<2> L2归一化(norm=l2):平方相加作为分母,特征值作为分子
<3> max归一化(norm=max):max作为分母,特征值作为分子
代码如下(示例):
python
#不用创建对象直接调用方法
#l1绝对值相加做分母
data_new= normalize(data,norm="l1",axis=1)
print(data_new)
#l2平方和做分母
data_new = normalize(data,norm="l2",axis=1)
print(data_new)
#max最大值做分母
data_new = normalize(data,norm="max",axis=1)
print(data_new)归一化效果:
l1归一化
[[0.5 0.34313725 0.1372549 0.01960784]
[0.51578947 0.31578947 0.14736842 0.02105263]
[0.5 0.34042553 0.13829787 0.0212766 ]
[0.4893617 0.32978723 0.15957447 0.0212766 ]
[0.49019608 0.35294118 0.1372549 0.01960784]]
l2归一化
[[0.80377277 0.55160877 0.22064351 0.0315205 ]
[0.82813287 0.50702013 0.23660939 0.03380134]
[0.80533308 0.54831188 0.2227517 0.03426949]
[0.80003025 0.53915082 0.26087943 0.03478392]
[0.790965 0.5694948 0.2214702 0.0316386 ]]
max归一化
[[1. 0.68627451 0.2745098 0.03921569]
[1. 0.6122449 0.28571429 0.04081633]
[1. 0.68085106 0.27659574 0.04255319]
[1. 0.67391304 0.32608696 0.04347826]
[1. 0.72 0.28 0.04 ]]3.标准化(Z-Score Scaling):StandardScaler(适合高斯分布数据)
在机器学习中,标准化是一种数据预处理技术,也称为数据归一化或特征缩放。它的目的是将不同特征的数值范围缩放到统一的标准范围,以便更好地适应一些机器学习算法,特别是那些对输入数据的尺度敏感的算法。
- <1>标准化公式
最常见的标准化方法是Z-score标准化,也称为零均值标准化。它通过对每个特征的值减去其均值,再除以其标准差,将数据转换为均值为0,标准差为1的分布。这可以通过以下公式计算:
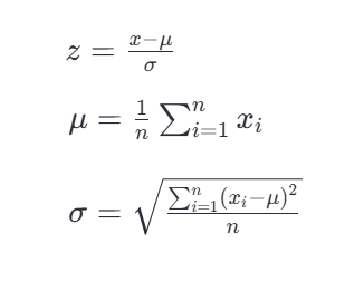
其中,z是转换后的数值,x是原始数据的值,μ是该特征的均值,σ是该特征的 标准差
-
<2> 标准化 API
sklearn.preprocessing.StandardScale
与MinMaxScaler一样,原始数据类型可以是list、DataFrame和ndarray
fit_transform函数的返回值为ndarray, 归一化后得到的数据类型都是ndarray
代码示例:
python
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
#获取数据集
iris = load_iris()
data = iris.data[:5]
#StandardScaler标准化
#创建标准化转换对象
transfer = StandardScaler()
#调用fit_transform
data_new = transfer.fit_transform(data)
print(data_new)标准化效果:
[[ 1.29399328 0.95025527 0. 0. ]
[ 0.21566555 -1.2094158 0. 0. ]
[-0.86266219 -0.34554737 -1.58113883 0. ]
[-1.40182605 -0.77748158 1.58113883 0. ]
[ 0.75482941 1.38218948 0. 0. ]]四、特征选择与降维
实际数据中,有时候特征很多,会增加计算量,降维就是去掉一些特征,或者转化多个特征为少量个特征
特征降维其目的:是减少数据集的维度,同时尽可能保留数据的重要信息。
特征降维的好处:
减少计算成本:在高维空间中处理数据可能非常耗时且计算密集。降维可以简化模型,降低训练时间和资源需求。
去除噪声:高维数据可能包含许多无关或冗余特征,这些特征可能引入噪声并导致过拟合。降维可以帮助去除这些不必要的特征。
特征降维的方式:
- 特征选择
- 从原始特征集中挑选出最相关的特征
- 主成份分析(PCA)
- 主成分分析就是把之前的特征通过一系列数学计算,形成新的特征,新的特征数量会小于之前特征数量
1.方差阈值法(VarianceThreshold)剔除低方差特征
-
Filter(过滤式): 主要探究特征本身特点, 特征与特征、特征与目标 值之间关联-
方差选择法: 低方差特征过滤
如果一个特征的方差很小,说明这个特征的值在样本中几乎相同或变化不大,包含的信息量很少,模型很难通过该特征区分不同的对象,比如区分甜瓜子和咸瓜子还是蒜香瓜子,如果有一个特征是长度,这个特征相差不大可以去掉。
- 计算方差:对于每个特征,计算其在训练集中的方差(每个样本值与均值之差的平方,在求平均)。
- 设定阈值:选择一个方差阈值,任何低于这个阈值的特征都将被视为低方差特征。
- 过滤特征:移除所有方差低于设定阈值的特征
-
代码示例:
python
from sklearn.datasets import load_iris
from sklearn.feature_selection import VarianceThreshold
import numpy as np
iris = load_iris()
X = iris.data[:10]
y = [1,1,1,0,0,0,1,0,1,1]
print(X)
#低反差过滤特征选择
#创建转换器对象
transfer1 = VarianceThreshold(threshold=0.01)
data_new = transfer1.fit_transform(X)
print(data_new)特征过滤前
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]]
经过低方差过滤后
[[5.1 3.5 1.4]
[4.9 3. 1.4]
[4.7 3.2 1.3]
[4.6 3.1 1.5]
[5. 3.6 1.4]
[5.4 3.9 1.7]
[4.6 3.4 1.4]
[5. 3.4 1.5]
[4.4 2.9 1.4]
[4.9 3.1 1.5]]2.皮尔逊相关系数(Pearson correlation coefficient)
皮尔逊相关系数(Pearson correlation coefficient)是一种度量两个变量之间线性相关性的统计量。它提供了两个变量间关系的方向(正相关或负相关)和强度的信息。皮尔逊相关系数的取值范围是 [−1,1],其中:
- ρ = 1 \rho=1 ρ=1 表示完全正相关,即随着一个变量的增加,另一个变量也线性增加。
- ρ = − 1 \rho=-1 ρ=−1 表示完全负相关,即随着一个变量的增加,另一个变量线性减少。
- ρ = 0 \rho=0 ρ=0 表示两个变量之间不存在线性关系。
相关系数
ρ \rho ρ
的绝对值为0-1之间,绝对值越大,表示越相关,当两特征完全相关时,两特征的值表示的向量是
在同一条直线上,当两特征的相关系数绝对值很小时,两特征值表示的向量接近在同一条直线上。当相关系值为负数时,表示负相关,皮尔逊相关系数:pearsonr相关系数计算公式, 该公式出自于概率论
对于两组数据 𝑋={𝑥1,𝑥2,...,𝑥𝑛} 和 𝑌={𝑦1,𝑦2,...,𝑦𝑛},皮尔逊相关系数可以用以下公式计算:
ρ = Cos ( x , y ) D x ⋅ D y = E [ ( x − E x ) ( y − E y ) ] D x ⋅ D y = ∑ i = 1 n ( x − x ~ ) ( y − y ˉ ) / ( n − 1 ) ∑ i = 1 n ( x − x ˉ ) 2 / ( n − 1 ) ⋅ ∑ i = 1 n ( y − y ˉ ) 2 / ( n − 1 ) \rho=\frac{\operatorname{Cos}(x, y)}{\sqrt{D x} \cdot \sqrt{D y}}=\frac{E[(x_-E x)(y-E y)]}{\sqrt{D x} \cdot \sqrt{D y}}=\frac{\sum_{i=1}^{n}(x-\tilde{x})(y-\bar{y}) /(n-1)}{\sqrt{\sum_{i=1}^{n}(x-\bar{x})^{2} /(n-1)} \cdot \sqrt{\sum_{i=1}^{n}(y-\bar{y})^{2} /(n-1)}} ρ=Dx ⋅Dy Cos(x,y)=Dx ⋅Dy E[(x−Ex)(y−Ey)]=∑i=1n(x−xˉ)2/(n−1) ⋅∑i=1n(y−yˉ)2/(n−1) ∑i=1n(x−x~)(y−yˉ)/(n−1)
x ˉ \bar{x} xˉ和 y ˉ \bar{y} yˉ 分别是𝑋和𝑌的平均值
|ρ|<0.4为低度相关; 0.4<=|ρ|<0.7为显著相关; 0.7<=|ρ|<1为高度相关
scipy.stats.personr(x, y) 计算两特征之间的相关性
返回对象有两个属性:
- statistic皮尔逊相关系数[-1,1]
- pvalue零假设(了解),统计上评估两个变量之间的相关性,越小越相关
代码示例:
python
from sklearn.datasets import load_iris
from scipy.stats import pearsonr
import numpy as np
iris = load_iris()
X = iris.data[:10]
y = [1,1,1,0,0,0,1,0,1,1]
#相关系数过滤特征选择
#将数据转为numpy数组提取每一列
del1 = np.array(X)[:,0]
print(del1)
print(y)
#pearsonr可以直接计算相关系数
r1 = pearsonr(del1,y)
#输出相关系数statistic 相关性:负数值表示负相关,正数表示正相关,0表示不相关
print(r1.statistic)
#输出相关系数pvalue 程度相关性:pvalue的值越小,则越相关
print(r1.pvalue)[5.1 4.9 4.7 4.6 5. 5.4 4.6 5. 4.4 4.9]
[1, 1, 1, 0, 0, 0, 1, 0, 1, 1]
-0.4135573338871735
0.23483566170378163.主成分分析(sklearn.decomposition.PCA)
-
用矩阵P对原始数据进行线性变换,得到新的数据矩阵Z,每一列就是一个主成分, 如下图就是把10维降成了2维,得到了两个主成分
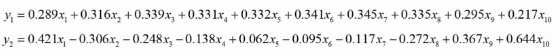
-
根据主成分的方差等,确定最终保留的主成分个数, 方差大的要留下。一个特征的多个样本的值如果都相同,则方差为0, 则说明该特征值不能区别样本,所以该特征没有用。
PCA(n_components=None)
-
主成分分析
-
n_components:
- 实参为小数时:表示降维后保留百分之多少的信息
- 实参为整数时:表示减少到多少特征
代码示例:
python
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
x,y = load_iris(return_X_y=True)
data = x[0:5]
print(data)
#创建转化器对象n_components为小数时表示保留原始数据80%的信息
transfer = PCA(n_components=0.8)
#调用转换器方法fit_transform()
data_new = transfer.fit_transform(data)
print(data_new)
#n_components为整数时表示保留的维度
transfer = PCA(n_components=2)
data_new = transfer.fit_transform(data)
print(data_new)执行效果:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
[[ 0.31871016]
[-0.20314124]
[-0.15458491]
[-0.30200277]
[ 0.34101876]]
[[ 0.31871016 0.06464364]
[-0.20314124 0.19680403]
[-0.15458491 -0.07751201]
[-0.30200277 -0.10904729]
[ 0.34101876 -0.07488837]]结语
特征工程是机器学习中的"艺术",需要领域知识、统计思维和编程技巧的结合。本文从 字典特征 到 PCA降维,系统介绍了特征工程的核心方法,并提供了可直接复用的代码示例。
🔧 动手挑战:尝试对一份真实数据集(如Kaggle的Titanic数据)进行完整的特征工程处理,观察模型效果的变化!
📚 下期预告:我们将进入 模型训练与调优 阶段,探讨如何选择算法并优化超参数。