2.1 Classification and Linear Discriminants
2.1 分类和线性判别器
2.2 Determining Linear Separability
2.2 确定线性可分性
分类器和线性可分
- [1 基础概念](#1 基础概念)
-
- [1.1 理论化](#1.1 理论化)
- [1.2 数学化](#1.2 数学化)
- [2 Discriminant based classification 基于判别式的分类](#2 Discriminant based classification 基于判别式的分类)
-
- [2.1 Linear Classifier 线性判别式 (supervised 监督)](#2.1 Linear Classifier 线性判别式 (supervised 监督))
- [2.2 KNN (K=3)-Nearest Neighbor Classification 最近邻分类器](#2.2 KNN (K=3)-Nearest Neighbor Classification 最近邻分类器)
- [3 Linear Separability 线性可分](#3 Linear Separability 线性可分)
-
- [3.1 记忆与泛化](#3.1 记忆与泛化)
1 基础概念
1.1 理论化
Training data : the data has been given to us in which we know the features of a given example as well as the corresponding labels of that example. 我们已经获得了数据,其中我们知道给定示例的特征以及该示例的相应标签。
Validation Data :Set of examples (with known labels) that are used to ensure that the classifier is
expected to generalize to novel cases 验证数据:一组具有已知标签的示例,用于确保分类器能够推广到新的案例
Test Data :(Ideally) Data for which the labels are not known and the ML model is used to find
their labels 测试数据:(理想情况下)标签未知的数据,可以使用机器学习模型来查找其标签。
Training Set(训练集)------用于训练模型
├── Validation Set(验证集)------用于调参、模型选择
└── Test Set(测试集)------仅用于最终性能评估
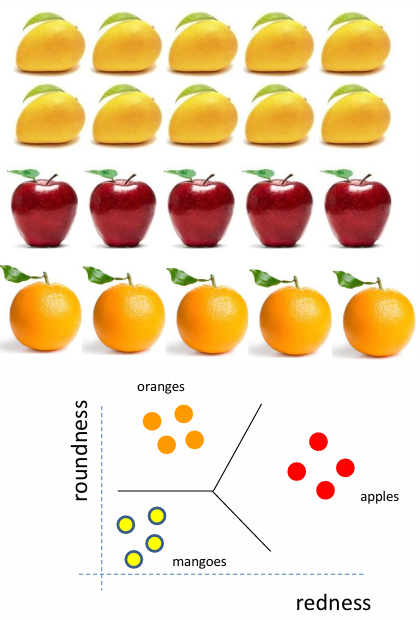
Training 训练:These objects span this feature space to make a rule that allows us to classify for this particular problem. The development of this rule is called training. 这些对象跨越特征空间,形成一个规则,使我们能够针对这个特定问题进行分类。这个规则的制定过程称为训练。
1.2 数学化
标签集 label class : y ∈ { c 1 , c 2 , ... , c M } y \in \{ c_1, c_2, \ldots, c_M \} y∈{c1,c2,...,cM}
在上述例子中,M=3, c 1 = o r a n g e s c_1 = oranges c1=oranges , c 2 = a p p l e s c_2 = apples c2=apples , c 3 = m a n g o e s c_3 = mangoes c3=mangoes 。
每个样本的特征向量(feature vector) :
x = [ x ( 1 ) x ( 2 ) ⋮ x ( d ) ] \mathbf{x} = \begin{bmatrix} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(d)} \end{bmatrix} x= x(1)x(2)⋮x(d)
对于一个橘子,其中 d=2,redness=1, roundness =3 (红度为1,圆度为3)
x = [ 1 3 ] \mathbf{x} = \begin{bmatrix} 1 \\ 3 \\ \end{bmatrix} x=[13]
由此,我们得到最终版本的分类数据点 classified data points,X数据集,Y标签集:
X = { x 1 , x 2 , ... , x N } , x i = [ x i ( 1 ) x i ( 2 ) ⋮ x i ( d ) ] X = \{ \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_N \}, \quad \mathbf{x}_i = \begin{bmatrix} x_i^{(1)} \\ x_i^{(2)} \\ \vdots \\ x_i^{(d)} \end{bmatrix} X={x1,x2,...,xN},xi= xi(1)xi(2)⋮xi(d)
Y = { y 1 , y 2 , ... , y N } , y i ∈ { c 1 , c 2 , ... , c M } Y = \{ y_1, y_2, \ldots, y_N \}, \quad y_i \in \{ c_1, c_2, \ldots, c_M \} Y={y1,y2,...,yN},yi∈{c1,c2,...,cM}
2 Discriminant based classification 基于判别式的分类
Discriminant is a very specific way of developing classifier. 判别式是一个非常具体的开发分类器的方式
在这种分类中,目标是从训练数据中学习一个函数,或者,如果类别超过 2 个,则学习一组函数,这些函数可以为测试数据生成决策,从而将数据中的类别区分开来。
类别标签分配:
c ( x ) = arg max k = 1 , ... , M f k ( x ) c(\mathbf{x}) = \arg\max_{k = 1, \ldots, M} f_k(\mathbf{x}) c(x)=argk=1,...,Mmaxfk(x)
上述例子,类别是苹果、橘子、芒果三类,使用三个函数 f 1 ( x ) f_1(x) f1(x), f 2 ( x ) f_2(x) f2(x), f 3 ( x ) f_3(x) f3(x)分别对应三个标签。把一个样本代入这三个函数,得到三个值。其中最大值是哪个函数,就对应哪个标签。
2.1 Linear Classifier 线性判别式 (supervised 监督)
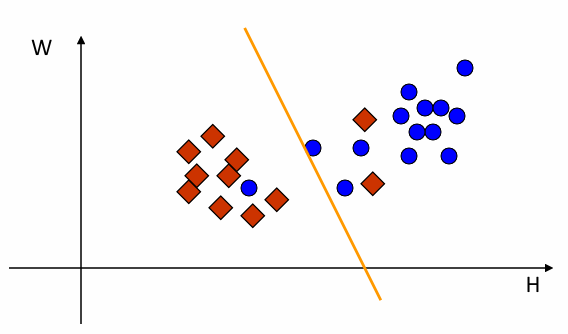
2.2 KNN (K=3)-Nearest Neighbor Classification 最近邻分类器
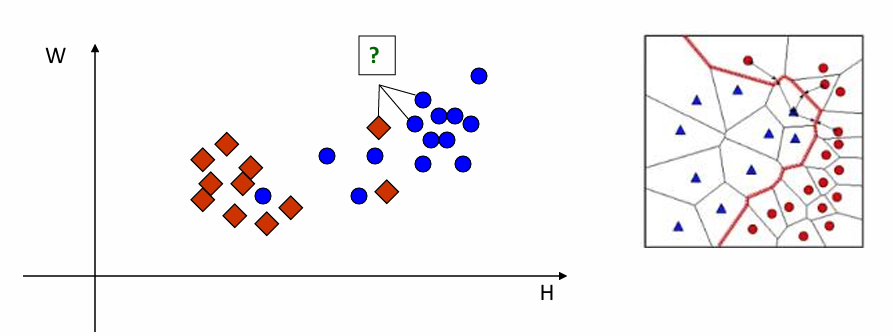
Note: K = 3构成的边界图比 K = 1更平滑smooth。
3 Linear Separability 线性可分
If data points can be separated by a linear discriminant then that dataset/classification problem is called "linearly separable" 如果数据点可以通过线性判别式分离,则该数据集/分类问题称为"线性可分"
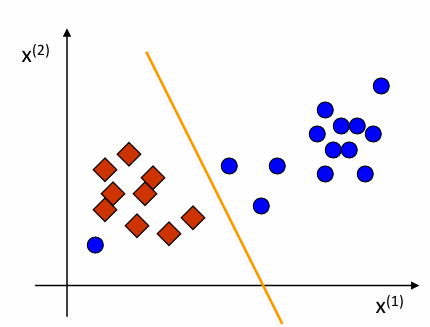
上图不是线性可分的,因为存在左下角蓝色圆点,当无法完全区分的时候,就不属于线性可分。
从数学上讲,如果存在一个线性函数,
f ( x ; w ) = w 1 x ( 1 ) + w 2 x ( 2 ) + ⋯ + w d x ( d ) + b = 0 f(\mathbf{x}; \mathbf{w}) = w_1 x^{(1)} + w_2 x^{(2)} + \cdots + w_d x^{(d)} + b = 0 f(x;w)=w1x(1)+w2x(2)+⋯+wdx(d)+b=0
满足,
如果标签 y i = + 1 y_i = +1 yi=+1,则 f ( x i ; w ) > 0 f(x_i; \mathbf{w}) > 0 f(xi;w)>0
如果标签 y i = − 1 y_i = -1 yi=−1,则 f ( x i ; w ) < 0 f(x_i; \mathbf{w}) < 0 f(xi;w)<0
这个数据集是线性可分的。
3.1 记忆与泛化
A particular issue in classification is the tradeoff between memorization vs. generalization 分类中的一个特殊问题是记忆与泛化之间的权衡
Remembering everything is not learning 记住一切并非学习
学习的真正考验在于处理相似但未见过的案例(泛化)The true test of learning is handling similar but unseen cases
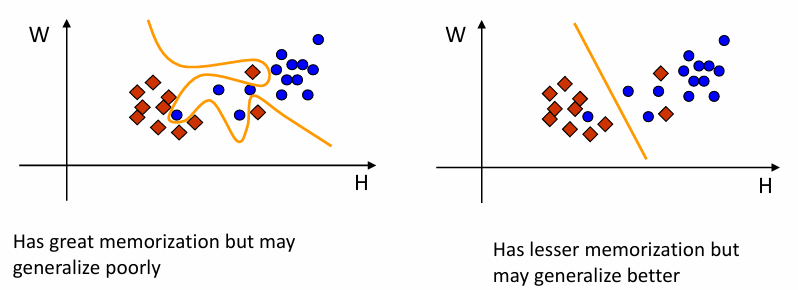
左图:记忆力强(分类效果好),但泛化能力差 【过拟合】
右图:记忆力差(分类效果差),但泛化能力强