知识结构总览
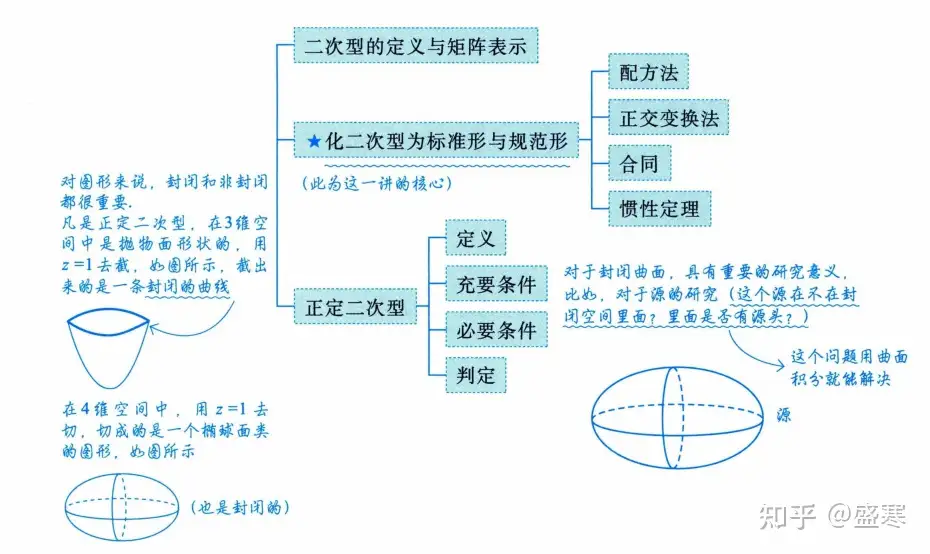
首先是我们的二次型的定义,就是说什么样的才算是一个二次型。然后就是如何把二次型化为标准型,最后就是正定二次型的定义和判断的一些条件。
二次型的定义

二次型其实是一种函数表达的方式,如上,含义其实就是每个项都是二次的,不存在更高和更低次的项。
考研只研究a是实数的情况,所以我们也可以说我们这里的二次型是实二次型。
在我们的线性代数中,所有的函数都可以把它表示成矩阵的形式。那我们把这里的f用矩阵表示就是:
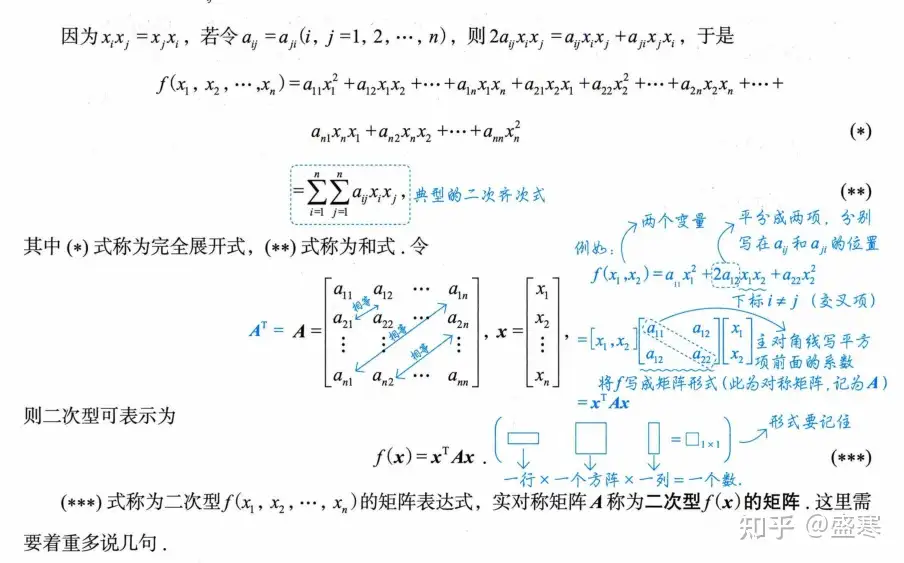
我们可以看到,其实一个二次型,最核心的就是里面的A,因为对所有的同型的二次型来说,他们的不同点就是A,所以这个A就是灵魂所在,我们说研究一个二次型的表达式f,其实就是在研究这里面的A。A 的秩就是f的秩。
另外,我们对这里的A有特殊 的规定,我们规定了二次型的矩阵A必须是对称矩阵。并且对于我们的A中元素的计算也有特别的规定:
主对角线上就是平方前的系数( 前的系数),其他位置则为对应位置的一半(比如这里的第一行第二列(对应的 )前面的系数就是-1(为-2的一半))

由于我们这里的A是对称矩阵,所以就有很多很好的性质可以用(参见上一章的最后一节)。这里就不多赘述了。
矩阵合同
线性变换的定义


简单来说其实就是x=Cy,但是之前我们说过,我们的二次型都是研究中间的那个系数矩阵(就是A),所以对于我们的线性变换而言,我们研究的也应该是中间的那个系数矩阵,也就是B。、
那么我们的A和B之间的关系应该就是我们线性变换的核心。
矩阵合同的定义合并性质

可以看到如果两个矩阵是合同的,那也就说明这两个矩阵是等价的,因为我们乘的是一个可逆矩阵。

标准形和规范形


在我们的二次型这章如何把一个一般的二次型化为标准形是我们的重要考点。
两个化标准形的方向
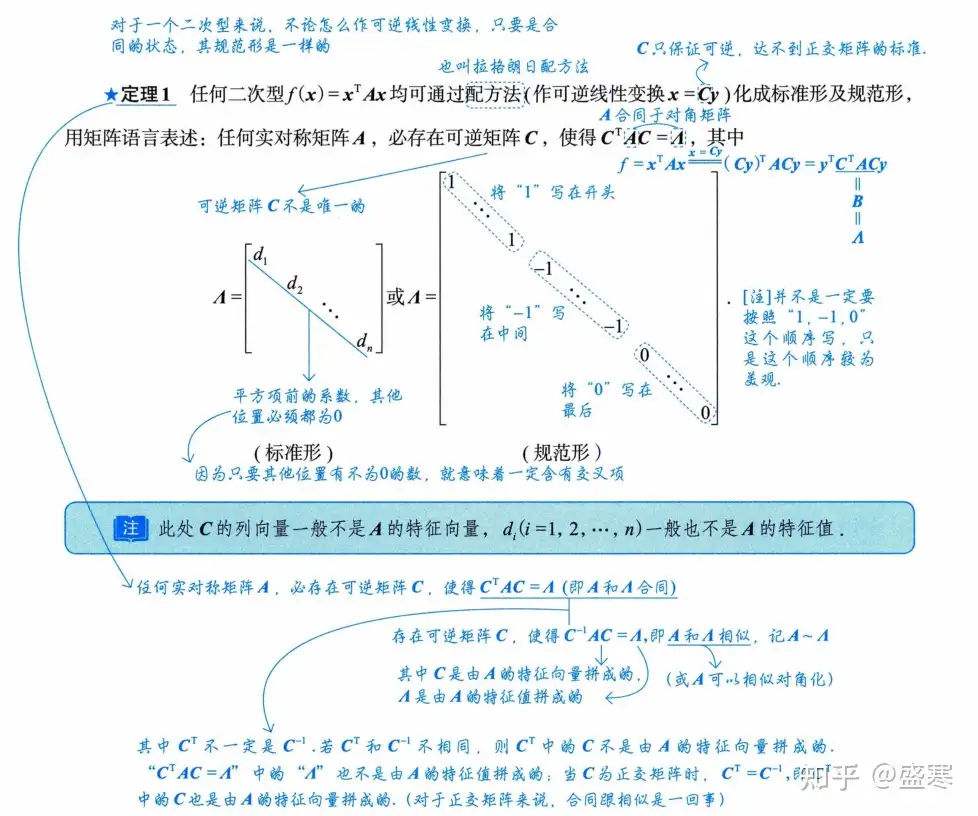

注意这两者的不同和相同点,首先是目标,我们都是希望找到一种线性变换让我们的二次型化为标准形,第一种的配方法找到的C虽然是可逆矩阵,但是和第二种的区别就在于第二种的C是正交矩阵,那么正交矩阵的性质和附带的内容是我们的第一种所没有的。
这两个方法的具体内容我们会在后面的小节中展开,大家稍安勿躁。
惯性定理
那么我们所谓的合同化为标准型形,既然我们的标准形并不是唯一的,我们之前说过相似和等价,他们都有自己不变的东西,那么请问我们的合同这个变换里不变的是什么呢?
简单来说就是合同的两个矩阵具有的特征值的正的个数和负的个数相同。请注意我们这里说的是正和负的个数都相同,而且是不包含0的。这里面正的个数我们称为正惯性指数, 负的个数我们称为负惯性指数。
小结

例题(配方法)
对于我们的配方法,我们的步骤是先找含有x1的,然后先配含有x1的部分,把x1配完,再找含x2的部分配完x2依次类推。
含有平方项
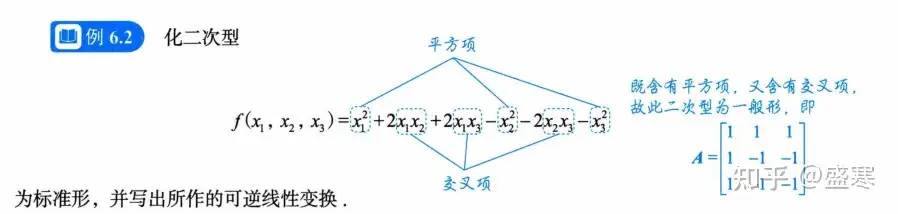

注意一点,使用配方法的时候一定要保证变量的个数不变,比如我们这题配方完之后就两个平方项,那么我们就要手动加上一个0*x3来保证变量的个数。
还有一点就是注意看我们这里的两个平方项,按照我们的步骤来的话,第一个平方里含有x1那么第二个平方必没有x2,因为我们的x1已经被我们配完了。所以这里要注意的是我们的配方不仅是要配成平方,其次还是有顺序的。那么如果有一个题目中他给你的是一个平方形式,我们也不要头脑一热以为这是给你配好的式子,我们还要看是不是按照顺序的(比如若第二个平方或者第三个平方里面包含了x1,那么这个就不是我们所说的配方法配成的标准形)
不含平方项
不含平方项我们就创造平方项然后按照我们之前的思路解题。

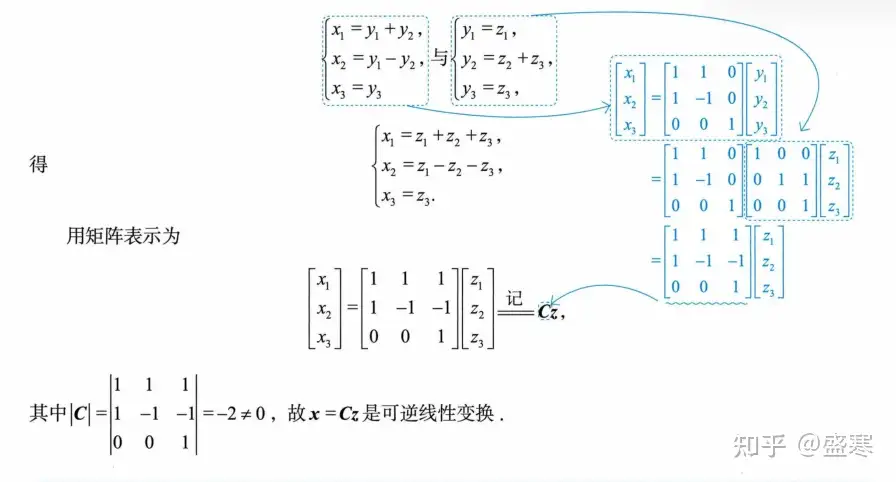
小结:

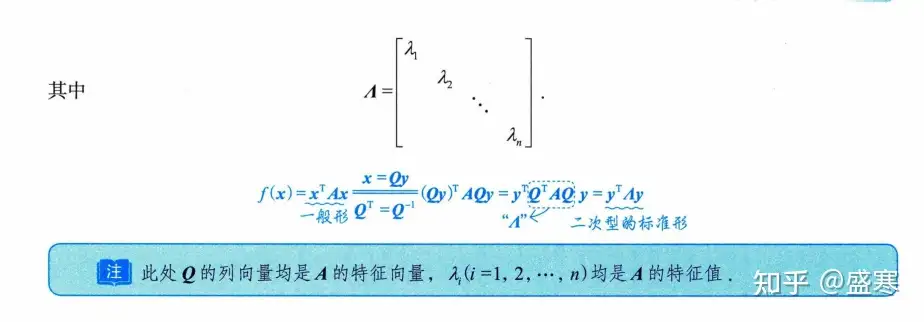
例题(正交变换法)
其实就是我们上一章最后讲的东西,所以这个方法有很多的性质。比如说求出来的答案中其标准形前面的系数就是特征值。Q是个正交矩阵,里面的就是由特征向量正交化(相同特征值正交化)单位化之后拼成的。


因为我们使用正交变换法之后的标准形有很多性质,所以呢题目也可能针对这些性质出题,比如说:
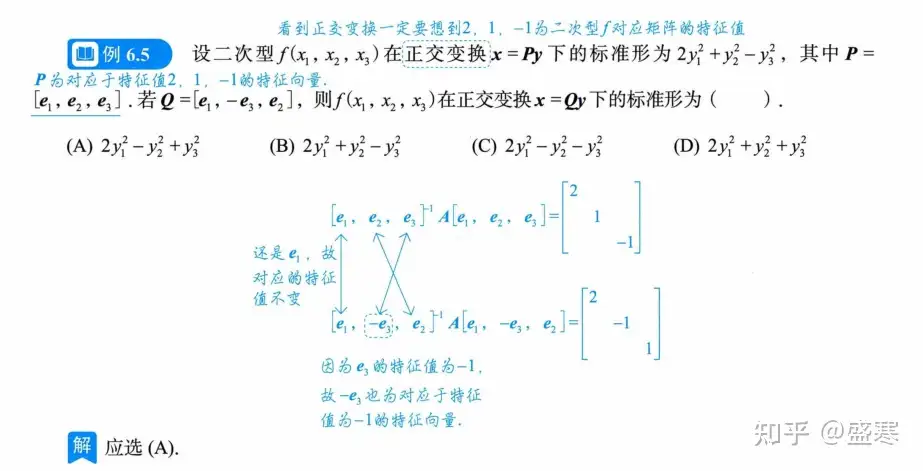
例题(其他一些知识点的考察)

看下这道题,首先我们只学过如何将一般形用线性变换变成一个标准形,没有学过这种把一般形变成一般形的。但是我们可不可以做呢?现在我们试一下。
首先是第一问,问的是a和b的值。a和b分别是A和B中的一个未知数,由于B是由A正交变换得到的,那么其实A和B也是相似的,既然相似,那么有很多性质我们就都可以用了。

第二问,我们只学过怎么把一个一般形的正交变换成标准形的,没学过其他的。注意我们考试是不会考超纲的题的,题目考察的一定是我们学过的知识点。对于我们没有头绪的同学可以尝试着把这两个都化成标准形。化完之后我们发现他俩是一样的。也就是说这两个最后的结果是一样的。也就是说第二个其实是第一个的中间状态,知道这个我们后面的解题也就水到渠成了。

还有一些题目考察我们合同中那个不变的性质以及我们的基本定义,还可以用来"套壳"考察我们前面的知识点。

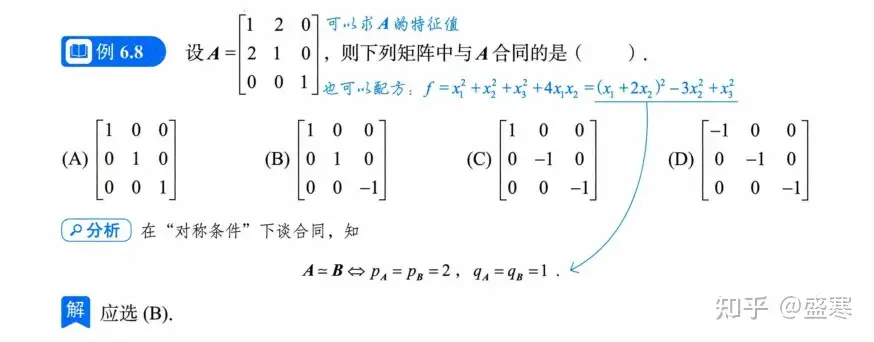

正定二次型及其判别
定义

注意必须是大于零(不能等于0),另外我们的正定是在二次型里面的,所以我们的正定矩阵也必须是对称矩阵。
条件
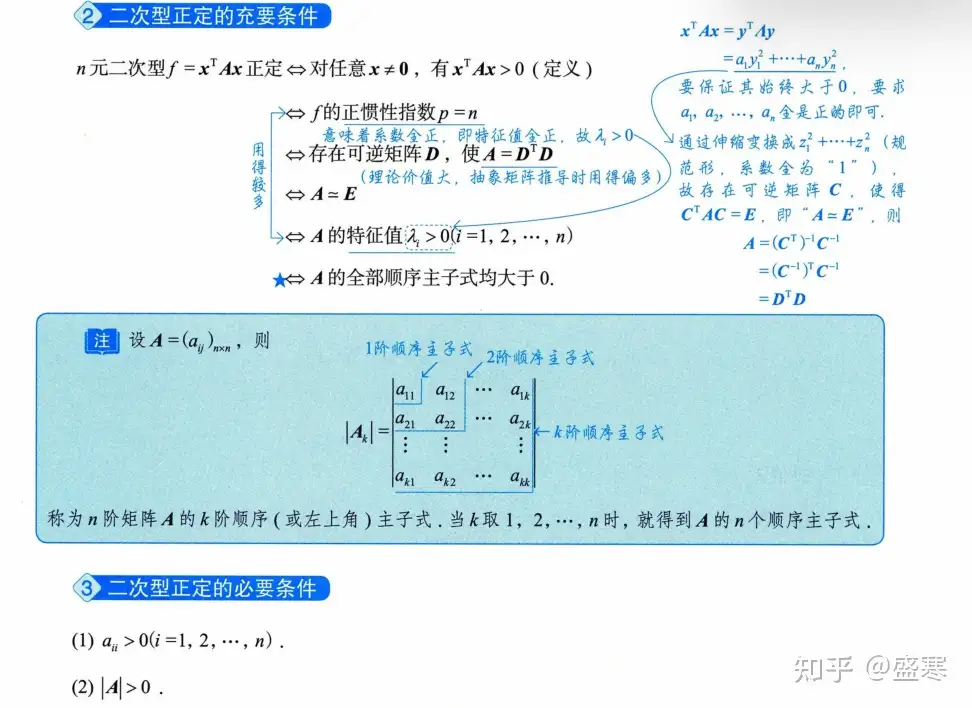
同样的,基本的考察就两个,一个是如何利用条件来判断正定,第二个也可以利用定义来判断正定。
例题
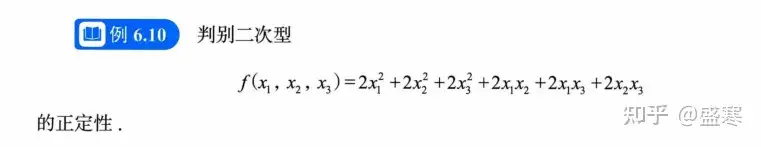



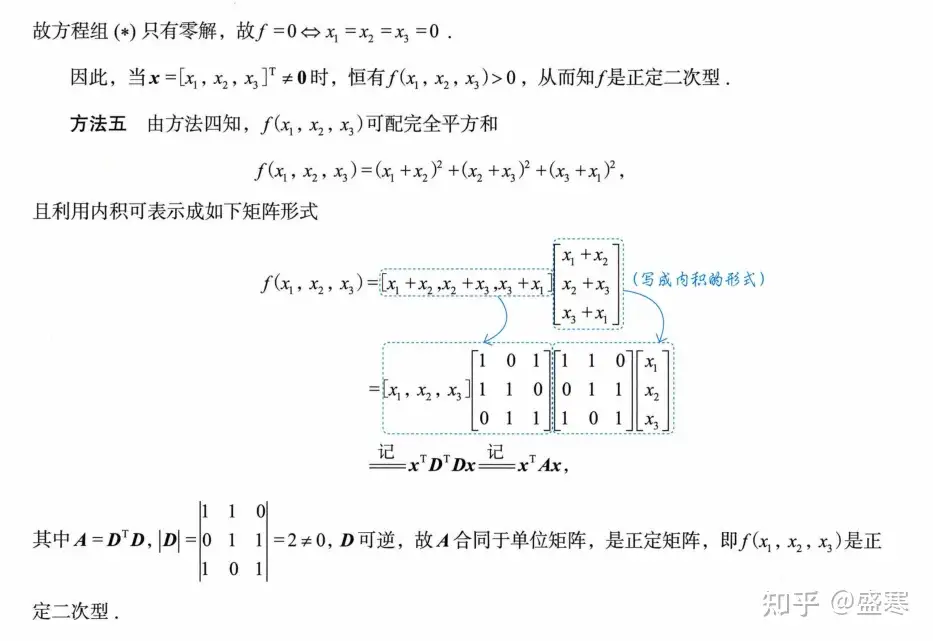

这几个方法大家都要过一遍,代表了我们基本的全部考法。